2021-2022学年沪教新版六年级上册数学《第4章 圆和扇形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年沪教新版六年级上册数学《第4章 圆和扇形》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 311.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览



文档简介
2021-2022学年沪教新版六年级上册数学《第4章
圆和扇形》单元测试卷
一.选择题
1.⊙O中,直径AB=a,弦CD=b,则a与b大小为( )
A.a>b
B.a≥b
C.a<b
D.a≤b
2.已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm
B.等于12cm
C.小于6cm
D.大于12cm
3.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
4.下列说法中,错误的是( )
A.半圆是弧
B.半径相等的圆是等圆
C.过圆心的线段是直径
D.直径是弦
5.点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
A.2
B.3
C.4
D.5
6.下列说法正确的是( )
A.三点确定一个圆
B.一个三角形只有一个外接圆
C.和半径垂直的直线是圆的切线
D.三角形的内心到三角形三个顶点距离相等
7.有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.
其中错误说法的个数是( )
A.1
B.2
C.3
D.4
8.一个商标图案如图中阴影部分,在长方形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积是( )
A.(4π+8)cm2
B.(4π+16)cm2
C.(3π+8)cm2
D.(3π+16)cm2
9.以下说法正确的个数有( )
①半圆是弧.
②三角形的角平分线是射线.
③在一个三角形中至少有一个角不大于60°.
④过圆内一点可以画无数条弦.
⑤所有角的度数都相等的多边形叫做正多边形.
A.1个
B.2个
C.3个
D.4个
10.如图中正方形、矩形、圆的面积相等,则周长L的大小关系是( )
A.LA>LB>LC
B.LA<LB<LC
C.LB>LC>LA
D.LC<LA<LB
二.填空题
11.到点A的距离为2cm的所有的点组成的图形是
.
12.到点P的距离等于6厘米的点的集合是
.
13.到定点A的距离等于3cm的点的轨迹是
.
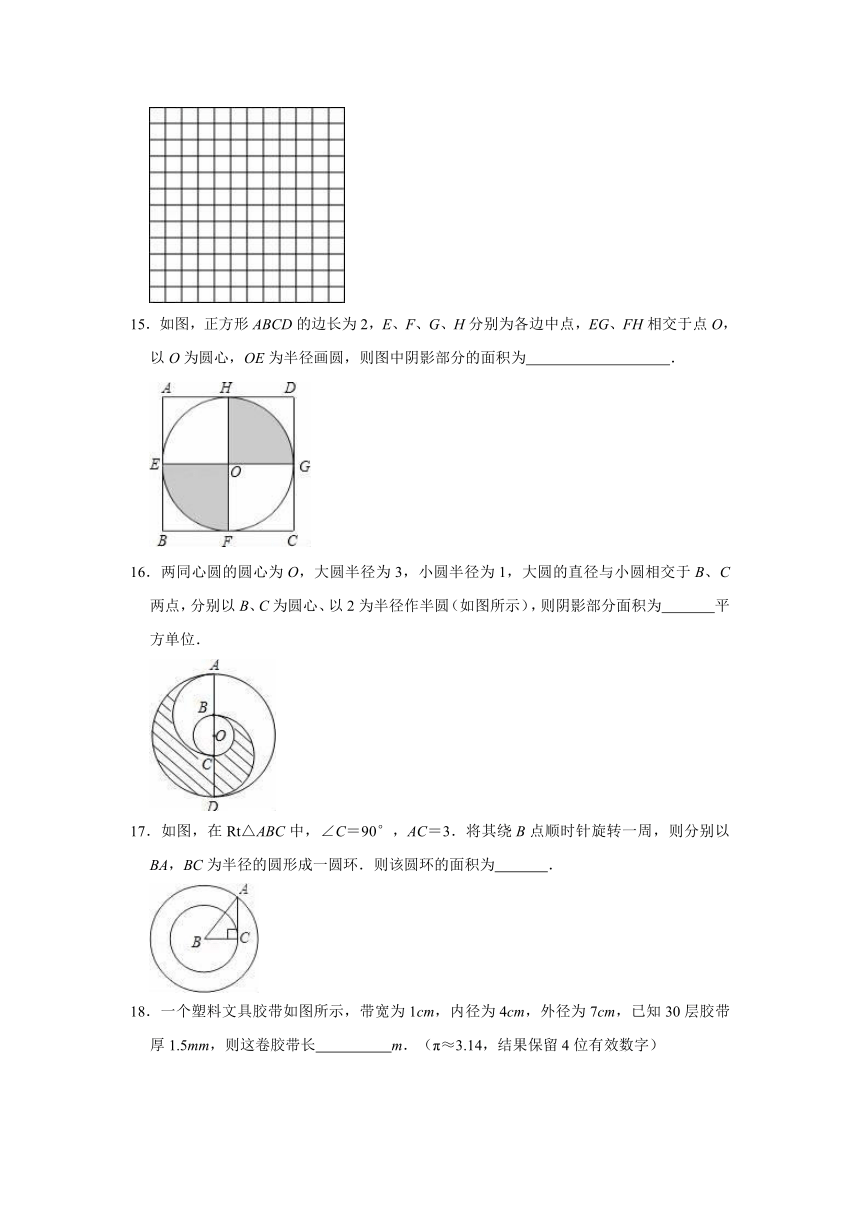
14.请你在如图所示的12×12的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的
个格点.
15.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为
.
16.两同心圆的圆心为O,大圆半径为3,小圆半径为1,大圆的直径与小圆相交于B、C两点,分别以B、C为圆心、以2为半径作半圆(如图所示),则阴影部分面积为
平方单位.
17.如图,在Rt△ABC中,∠C=90°,AC=3.将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.则该圆环的面积为
.
18.一个塑料文具胶带如图所示,带宽为1cm,内径为4cm,外径为7cm,已知30层胶带厚1.5mm,则这卷胶带长
m.(π≈3.14,结果保留4位有效数字)
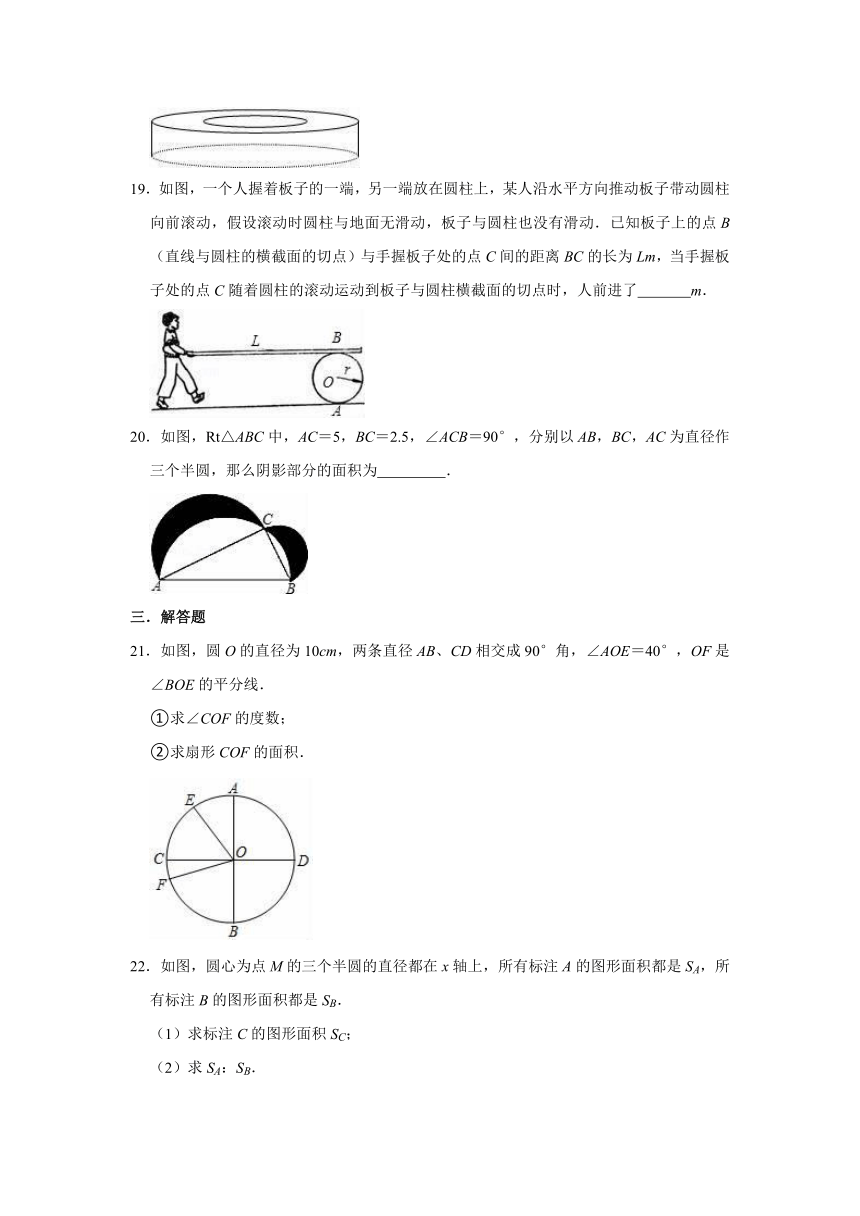
19.如图,一个人握着板子的一端,另一端放在圆柱上,某人沿水平方向推动板子带动圆柱向前滚动,假设滚动时圆柱与地面无滑动,板子与圆柱也没有滑动.已知板子上的点B(直线与圆柱的横截面的切点)与手握板子处的点C间的距离BC的长为Lm,当手握板子处的点C随着圆柱的滚动运动到板子与圆柱横截面的切点时,人前进了
m.
20.如图,Rt△ABC中,AC=5,BC=2.5,∠ACB=90°,分别以AB,BC,AC为直径作三个半圆,那么阴影部分的面积为
.
三.解答题
21.如图,圆O的直径为10cm,两条直径AB、CD相交成90°角,∠AOE=40°,OF是∠BOE的平分线.
①求∠COF的度数;
②求扇形COF的面积.
22.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
23.在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
24.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长;
(2)把AB分成三条相等的线段,每个小圆的周长l3=
;
(3)把AB分成四条相等的线段,每个小圆的周长l4=
;
(4)把AB分成n条相等的线段,每个小圆的周长ln=
.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的
.请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
25.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
参考答案与试题解析
一.选择题
1.解:直径是圆中最长的弦,因而有a≥b.
故选:B.
2.解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP=12.
故选:B.
3.解:以AB为直径的半圆的长是:π?AB;
设四个小半圆的直径分别是a,b,c,d,则a+b+c+d=AB.
则老鼠行走的路径长是:
a+πb+πc+πd=π(a+b+c+d)=π?AB.
故猫和老鼠行走的路径长相同.
故选:C.
4.解:A、半圆是弧,所以A选项的说法正确;
B、半径相等的圆是等圆,所以B选项的说法正确;
C、过圆心的弦为直径,所以C选项的说法错误;
D、直径是弦,所以D选项的说法正确.
故选:C.
5.解:由图可知,点A、B、E、C是⊙O上的点,
图中的弦有AB、BC、CE,一共3条.
故选:B.
6.解:A、不共线的三点确定一个圆,所以A选项错误;
B、一个三角形只有一个外接圆,所以B选项正确;
C、过半径的外端与半径垂直的直线是圆的切线,所以C选项错误;
D、三角形的内心到三角形三边的距离相等,所以D选项错误.
故选:B.
7.解:①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选:B.
8.解:作辅助线DE、EF使BCEF为一矩形.
则S△CEF=(8+4)×4÷2=24cm2,
S正方形ADEF=4×4=16cm2,
S扇形ADF==4πcm2,
∴阴影部分的面积=24﹣(16﹣4π)=8+4π(cm2).
故选:A.
9.解:圆的任意一条直径的端点把圆分成两条弧,每一条弧都叫做半圆,故①正确;
根据三角形角平分线的定义可知,三角形的角平分线是一条线段,故②错误;
在一个三角形中至少有一个角不大于60°,故③正确;
过圆内一点可以画无数条弦,故④正确;
矩形的四个角都相等,都等于90°,而矩形不是正四边形,故⑤错误;
故选:C.
10.解:设面积是S.
则正方形的边长是,则周长LA=4=;
长方形的一边长x,则另一边长为,则周长LB=2(x+),
∵(﹣)2≥0
∴x+≥2,
∴LB≥4,
即LB≥;
圆的半径为,LC=2π×=,
∵<,
∴LC<LA<LB.
故选:D.
二.填空题
11.解:到点A的距离为2cm的所有的点组成的图形是:以点A为圆心,2cm长为半径的圆.
12.解:到点P的距离等于6cm的点的集合是以P为圆心,以6cm为半径的圆.
故答案为:以P为圆心,以6cm为半径的圆.
13.解:到定点A的距离等于3cm的点的轨迹是:以A为圆心,以3cm为半径的圆.
故答案是:以A为圆心,以3cm为半径的圆.
14.解:如图,画半径为5的圆,可知圆最多能经过169个格点中的12个格点.
故答案为:12.
15.解:由题意可得:OE=1,
阴影面积==.
16.解:∵OA=OD=3,OB=OC=1,
∴AC=BD=4,
∴⊙B和⊙C是等圆,
∴S⊙B=S⊙C,
∴S阴影=S大⊙O﹣S小⊙O=(π×9﹣π×1)=4π.
17.解:圆环的面积=π?AB2﹣π?BC2=π(AB2﹣BC2),在直角△ABC中,根据勾股定理得到AC2=AB2﹣BC2,因而圆环的面积是π?AC2=9π.
18.解:4÷2=2(cm),
7÷2=3.5(cm),
胶带的体积是:π(3.52﹣22)?1=8.25πcm3=8.25π×10﹣6(m3),
一米长的胶带的体积是:0.01×1×5×10﹣5=5×10﹣7(m3),
因而胶带长是:(8.25π×10﹣6)÷(5×10﹣7)≈51.81(m).
故答案为:51.81.
19.解:因为圆向前滚动的距离是Lm,所以人前进了2Lm.
20.解:S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC﹣直径为AB的半圆的面积
=π()2+π()2+AC×BC﹣π()2
=πAC2+πBC2﹣πAB2+AC×BC
=π(AC2+BC2﹣AB2)+AC×BC
=AC×BC
=×5×2.5
=6.25.
故答案为:6.25.
三.解答题
21.解:①∵∠AOB=180°,∠AOE=40°,
∴∠BOE=140°,
∴OF是∠BOE的平分线,
∴,
∵两条直径AB,CD相交成90°角,
∴∠COF=90°﹣70°=20°;
②扇形COF的面积=.
22.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.(1分)
(2)
∴(3分)
∵
∴(5分)
∴
即SA:SB=5:6(6分)
23.解:(1)直线DA与图形W的公共点的个数为1个;
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点,
∵到点P的距离等于a的所有点组成图形W,
∴图形W是以点P为圆心,a为半径的圆,
根据题意补全图形如图所示,
连接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵点D到点A的距离也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA为⊙P的切线,
∴直线DA与图形W的公共点的个数为1个;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴点C在⊙P上,
∵AE⊥BD交图形W于点E,
∴=,
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=.
24.解:(2)l;
(3)l;
(4)l;;
每个小圆面积=π(?a)2=?,而大圆的面积=π(?a)2=πa2
即每个小圆的面积是大圆的面积的.
25.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
圆和扇形》单元测试卷
一.选择题
1.⊙O中,直径AB=a,弦CD=b,则a与b大小为( )
A.a>b
B.a≥b
C.a<b
D.a≤b
2.已知⊙O的半径为6cm,P为线段OA的中点,若点P在⊙O上,则OA的长( )
A.等于6cm
B.等于12cm
C.小于6cm
D.大于12cm
3.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地
B.老鼠先到达B地
C.猫和老鼠同时到达B地
D.无法确定
4.下列说法中,错误的是( )
A.半圆是弧
B.半径相等的圆是等圆
C.过圆心的线段是直径
D.直径是弦
5.点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
A.2
B.3
C.4
D.5
6.下列说法正确的是( )
A.三点确定一个圆
B.一个三角形只有一个外接圆
C.和半径垂直的直线是圆的切线
D.三角形的内心到三角形三个顶点距离相等
7.有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.
其中错误说法的个数是( )
A.1
B.2
C.3
D.4
8.一个商标图案如图中阴影部分,在长方形ABCD中,AB=8cm,BC=4cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积是( )
A.(4π+8)cm2
B.(4π+16)cm2
C.(3π+8)cm2
D.(3π+16)cm2
9.以下说法正确的个数有( )
①半圆是弧.
②三角形的角平分线是射线.
③在一个三角形中至少有一个角不大于60°.
④过圆内一点可以画无数条弦.
⑤所有角的度数都相等的多边形叫做正多边形.
A.1个
B.2个
C.3个
D.4个
10.如图中正方形、矩形、圆的面积相等,则周长L的大小关系是( )
A.LA>LB>LC
B.LA<LB<LC
C.LB>LC>LA
D.LC<LA<LB
二.填空题
11.到点A的距离为2cm的所有的点组成的图形是
.
12.到点P的距离等于6厘米的点的集合是
.
13.到定点A的距离等于3cm的点的轨迹是
.
14.请你在如图所示的12×12的网格图形中任意画一个圆,则所画的圆最多能经过169个格点中的
个格点.
15.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为
.
16.两同心圆的圆心为O,大圆半径为3,小圆半径为1,大圆的直径与小圆相交于B、C两点,分别以B、C为圆心、以2为半径作半圆(如图所示),则阴影部分面积为
平方单位.
17.如图,在Rt△ABC中,∠C=90°,AC=3.将其绕B点顺时针旋转一周,则分别以BA,BC为半径的圆形成一圆环.则该圆环的面积为
.
18.一个塑料文具胶带如图所示,带宽为1cm,内径为4cm,外径为7cm,已知30层胶带厚1.5mm,则这卷胶带长
m.(π≈3.14,结果保留4位有效数字)
19.如图,一个人握着板子的一端,另一端放在圆柱上,某人沿水平方向推动板子带动圆柱向前滚动,假设滚动时圆柱与地面无滑动,板子与圆柱也没有滑动.已知板子上的点B(直线与圆柱的横截面的切点)与手握板子处的点C间的距离BC的长为Lm,当手握板子处的点C随着圆柱的滚动运动到板子与圆柱横截面的切点时,人前进了
m.
20.如图,Rt△ABC中,AC=5,BC=2.5,∠ACB=90°,分别以AB,BC,AC为直径作三个半圆,那么阴影部分的面积为
.
三.解答题
21.如图,圆O的直径为10cm,两条直径AB、CD相交成90°角,∠AOE=40°,OF是∠BOE的平分线.
①求∠COF的度数;
②求扇形COF的面积.
22.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
23.在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
24.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长;
(2)把AB分成三条相等的线段,每个小圆的周长l3=
;
(3)把AB分成四条相等的线段,每个小圆的周长l4=
;
(4)把AB分成n条相等的线段,每个小圆的周长ln=
.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的
.请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
25.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
参考答案与试题解析
一.选择题
1.解:直径是圆中最长的弦,因而有a≥b.
故选:B.
2.解:根据点和圆的位置关系,得OP=6,再根据线段的中点的概念,得OA=2OP=12.
故选:B.
3.解:以AB为直径的半圆的长是:π?AB;
设四个小半圆的直径分别是a,b,c,d,则a+b+c+d=AB.
则老鼠行走的路径长是:
a+πb+πc+πd=π(a+b+c+d)=π?AB.
故猫和老鼠行走的路径长相同.
故选:C.
4.解:A、半圆是弧,所以A选项的说法正确;
B、半径相等的圆是等圆,所以B选项的说法正确;
C、过圆心的弦为直径,所以C选项的说法错误;
D、直径是弦,所以D选项的说法正确.
故选:C.
5.解:由图可知,点A、B、E、C是⊙O上的点,
图中的弦有AB、BC、CE,一共3条.
故选:B.
6.解:A、不共线的三点确定一个圆,所以A选项错误;
B、一个三角形只有一个外接圆,所以B选项正确;
C、过半径的外端与半径垂直的直线是圆的切线,所以C选项错误;
D、三角形的内心到三角形三边的距离相等,所以D选项错误.
故选:B.
7.解:①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选:B.
8.解:作辅助线DE、EF使BCEF为一矩形.
则S△CEF=(8+4)×4÷2=24cm2,
S正方形ADEF=4×4=16cm2,
S扇形ADF==4πcm2,
∴阴影部分的面积=24﹣(16﹣4π)=8+4π(cm2).
故选:A.
9.解:圆的任意一条直径的端点把圆分成两条弧,每一条弧都叫做半圆,故①正确;
根据三角形角平分线的定义可知,三角形的角平分线是一条线段,故②错误;
在一个三角形中至少有一个角不大于60°,故③正确;
过圆内一点可以画无数条弦,故④正确;
矩形的四个角都相等,都等于90°,而矩形不是正四边形,故⑤错误;
故选:C.
10.解:设面积是S.
则正方形的边长是,则周长LA=4=;
长方形的一边长x,则另一边长为,则周长LB=2(x+),
∵(﹣)2≥0
∴x+≥2,
∴LB≥4,
即LB≥;
圆的半径为,LC=2π×=,
∵<,
∴LC<LA<LB.
故选:D.
二.填空题
11.解:到点A的距离为2cm的所有的点组成的图形是:以点A为圆心,2cm长为半径的圆.
12.解:到点P的距离等于6cm的点的集合是以P为圆心,以6cm为半径的圆.
故答案为:以P为圆心,以6cm为半径的圆.
13.解:到定点A的距离等于3cm的点的轨迹是:以A为圆心,以3cm为半径的圆.
故答案是:以A为圆心,以3cm为半径的圆.
14.解:如图,画半径为5的圆,可知圆最多能经过169个格点中的12个格点.
故答案为:12.
15.解:由题意可得:OE=1,
阴影面积==.
16.解:∵OA=OD=3,OB=OC=1,
∴AC=BD=4,
∴⊙B和⊙C是等圆,
∴S⊙B=S⊙C,
∴S阴影=S大⊙O﹣S小⊙O=(π×9﹣π×1)=4π.
17.解:圆环的面积=π?AB2﹣π?BC2=π(AB2﹣BC2),在直角△ABC中,根据勾股定理得到AC2=AB2﹣BC2,因而圆环的面积是π?AC2=9π.
18.解:4÷2=2(cm),
7÷2=3.5(cm),
胶带的体积是:π(3.52﹣22)?1=8.25πcm3=8.25π×10﹣6(m3),
一米长的胶带的体积是:0.01×1×5×10﹣5=5×10﹣7(m3),
因而胶带长是:(8.25π×10﹣6)÷(5×10﹣7)≈51.81(m).
故答案为:51.81.
19.解:因为圆向前滚动的距离是Lm,所以人前进了2Lm.
20.解:S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC﹣直径为AB的半圆的面积
=π()2+π()2+AC×BC﹣π()2
=πAC2+πBC2﹣πAB2+AC×BC
=π(AC2+BC2﹣AB2)+AC×BC
=AC×BC
=×5×2.5
=6.25.
故答案为:6.25.
三.解答题
21.解:①∵∠AOB=180°,∠AOE=40°,
∴∠BOE=140°,
∴OF是∠BOE的平分线,
∴,
∵两条直径AB,CD相交成90°角,
∴∠COF=90°﹣70°=20°;
②扇形COF的面积=.
22.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.(1分)
(2)
∴(3分)
∵
∴(5分)
∴
即SA:SB=5:6(6分)
23.解:(1)直线DA与图形W的公共点的个数为1个;
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点,
∵到点P的距离等于a的所有点组成图形W,
∴图形W是以点P为圆心,a为半径的圆,
根据题意补全图形如图所示,
连接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵点D到点A的距离也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA为⊙P的切线,
∴直线DA与图形W的公共点的个数为1个;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴点C在⊙P上,
∵AE⊥BD交图形W于点E,
∴=,
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=.
24.解:(2)l;
(3)l;
(4)l;;
每个小圆面积=π(?a)2=?,而大圆的面积=π(?a)2=πa2
即每个小圆的面积是大圆的面积的.
25.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
