第4章一元一次方程单元测试题2020-2021学年苏科版七年级上册(word版含解析)
文档属性
| 名称 | 第4章一元一次方程单元测试题2020-2021学年苏科版七年级上册(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 156.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 06:32:01 | ||
图片预览




文档简介
一元一次方程单元测试题
学校:________ 班级:________ 姓名:________ 学号:________
一、单选题(共8小题)
1.七年级学生人数为x,其中男生占52%,女生有150人,下列正确的是( )
A.1﹣52%x=150 B.x=150﹣52%x
C.(1+52%)x=150 D.(1﹣52%)x=150
2.“某学校七年级学生人数为n,其中男生占55%,女生共有110人.”下列方程能表示上述语句中的相等关系的有( )
①(1﹣55%)n=110;②1﹣55%=;③55%=1﹣;④n=;⑤1=+55%.
A.2个 B.3个 C.4个 D.5个
3.若关于y的一元一次方程的解是y=﹣2,则a的值是( )
A.﹣50 B.﹣40 C.40 D.50
4.若方程3+▲=2x的解为x=5,则▲=( )
A.9 B.7 C.5 D.4
5.将方程﹣=1去分母得到2(2x﹣1)﹣3x+1=6错在( )
A.最简公分母找错
B.去分母时分子部分没有加括号
C.去分母时漏乘3项
D.去分母时各项所乘的数不同
6.某商店在某一时间以200元的价格卖出两件衣服,其中一件盈利25%,另一件亏损20%,那么商店在这次交易中( )
A.亏了10元钱 B.亏了20元钱 C.盈利20元钱 D.不赢不亏
7.有一个不完整圆柱形玻璃密封容器如图①,测得其底面半径为a,高为h,其内装蓝色液体若干.若如图②放置时,测得液面高为h;若如图3放置时,测得液面高为h.则该玻璃密封容器的容积(圆柱体容积=底面积×高)是( )
A. B. C. D.
8.若关于x的方程(k﹣2019)x﹣2017=7﹣2019(x+1)的解是整数,则整数k的取值个数是( )
A.2 B.3 C.4 D.6
二、填空题(共8小题)
9.下列各式中,化简后是一元一次方程的是 .
①x﹣1=3;②2x﹣y=5;③﹣y=﹣2;④x+3﹣4x;⑤x=0.
10.轮船沿江从A港顺流行驶到B港,比从B港返回少用3h.若船速为26km/h,水速为2km/h,设A港和B港相距xkm,列方程得: .
11.王涵同学在解关于x的方程7a+x=18时,误将+x看作﹣x,得方程的解为x=﹣4,那么原方程的解为 .
12.《算法统宗》中记有“李白沽酒”的故事.诗云:今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士:如何知原有?(古代一斗是10升)
大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.则李白的酒壶中原有 升酒.
13.a,b,c,d为有理数,现规定一种运算:=ad﹣bc,那么当=22时x的值是 .
14.一件商品标价140元,若八折出售,仍可获利12%,则这件商品的进价为 元.
15.如图,甲、乙两个动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点按顺时针方向环形运动,乙点按逆时针方向环形运动.若甲的速度是乙的速度的3倍.则它们第2019次相遇在边 上.
16.5个人用5天完成了某项工程的,如果再增加工作效率相同的10个人,那么完成这项工作前后共用 天.
三、解答题(共10小题)
17.解方程:
(1)1﹣2(2x+3)=﹣3(2x+1);
(2)﹣=1.
18.解方程:
(1)2(x+1)=1﹣(x+3).
(2)+1=.
19.解方程:
(1)3x﹣7(x﹣1)=3﹣2(x+3);
(2)﹣=1+.
20.现有180件机器零件需加工,任务由甲、乙两个小组合作完成,甲先加工,乙后加工,甲组每天加工12件,乙组每天加工8件,结果共用20天完成任务.求甲、乙两组分别加工机器零件多少个.
21.温州苍南马站四季柚,声名远播,今年又是一个丰收年.某经销商为了打开销路,对1000个四季柚进行打包优惠出售.打包方式及售价如图.假设用这两种打包方式恰装完全部柚子.
(1)若销售a箱纸盒装和a袋编织袋装四季柚的收入共950元,求a的值.
(2)当销售总收入为7280元时.
①若这批四季柚全部售完,请问纸盒装共包装了多少箱,编织袋共包装了多少袋?
②若该经销商留下b(b>0)箱纸盒装送人,其余纸盒全部售出,求b的值.
22.某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:买一套西装赠送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)①若该用户按方案一购买,需付款 元(用含x的式子表示);
②若该用户按方案二购买,需付款 元(用含x的式子表示);
(2)①若x=30,通过计算说明此时按哪种方案购买比较合算?
②当x= 时,两种购买方案付款相同.
23.如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为4,点P从点A出发以每秒2个单位长度的速度在数轴上由点A到点B方向运动,当点P到达点B后立即返回,仍然以2个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒)
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P由点A到点B的运动过程中,求点P与点A的距离(用含t的代数式表示);在点P由点B到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,直接写出所有满足条件的t值.
24.阅读下列材料:
现规定一种运算:=ad﹣bc.
例如:=1×4﹣2×3=4﹣6=﹣2;=4x﹣(﹣2)×3=4x+6.
按照这种规定的运算,请解答下列问题:
(1)= (只填结果);
(2)已知:=1.求x的值.(写出解题过程)
25.如图:是某月份的月历表,请你认真观察月历表,回答以下问题:
(1)如果圈出同一行的三个数,用a表示中间的数,则第一个数,第三个数怎样表示?
(2)如果圈出同一列的三个数,用a表示中间的数,则第一个数,第三个数怎样表示?
(3)如果圈出如图所示的任意9个数,这9个数的和可能是207吗?如果可能,请求出这9个数;如果不可能,请说明理由.
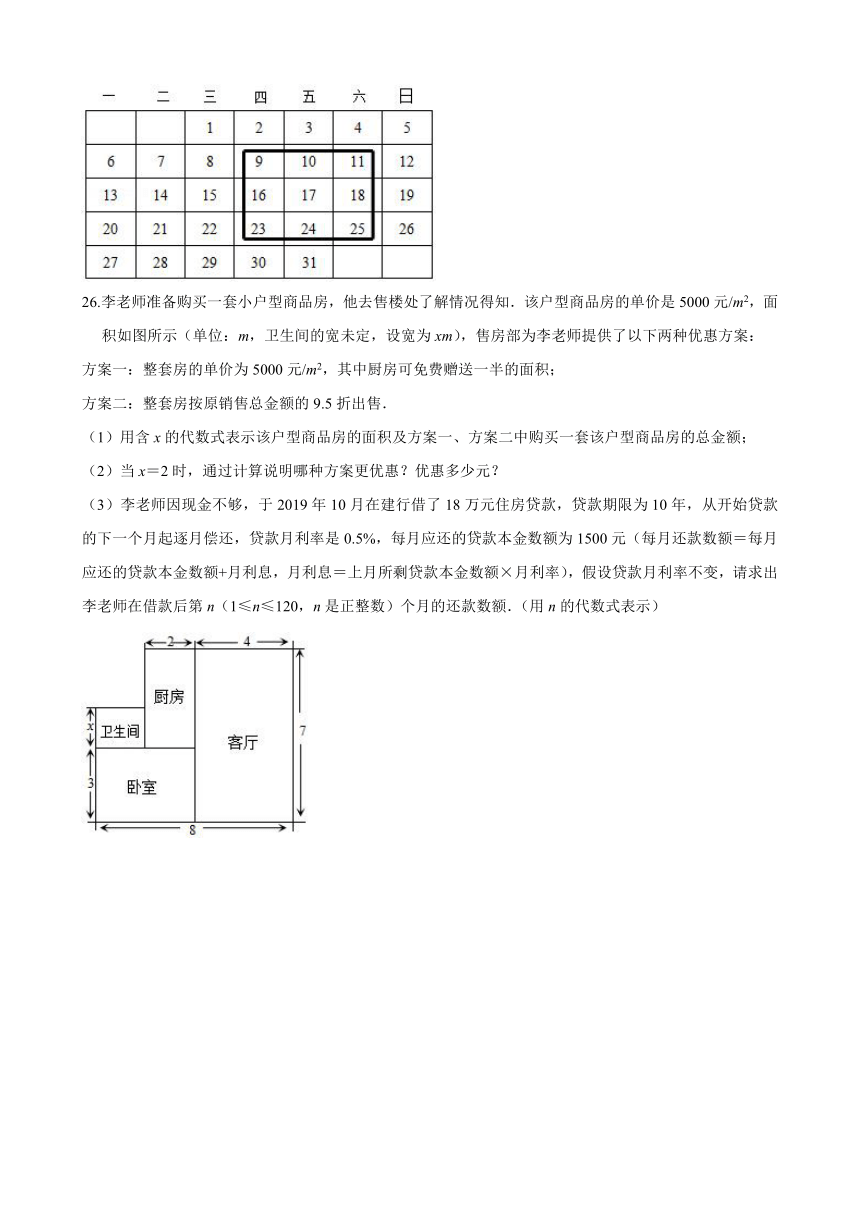
26.李老师准备购买一套小户型商品房,他去售楼处了解情况得知.该户型商品房的单价是5000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李老师提供了以下两种优惠方案:
方案一:整套房的单价为5000元/m2,其中厨房可免费赠送一半的面积;
方案二:整套房按原销售总金额的9.5折出售.
(1)用含x的代数式表示该户型商品房的面积及方案一、方案二中购买一套该户型商品房的总金额;
(2)当x=2时,通过计算说明哪种方案更优惠?优惠多少元?
(3)李老师因现金不够,于2019年10月在建行借了18万元住房贷款,贷款期限为10年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月应还的贷款本金数额为1500元(每月还款数额=每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率),假设贷款月利率不变,请求出李老师在借款后第n(1≤n≤120,n是正整数)个月的还款数额.(用n的代数式表示)
一元一次=方程单元测试题
参考答案
一、单选题(共8小题)
1.【答案】 D
【解答】 解:由题意得:(1﹣52%)x=150,
故选:D.
2.【答案】 D
【解答】 解:男生人数为(n﹣110),
∴55%n=n﹣110,
∴(1﹣55%)n=110,
1﹣55%=,
55%=1﹣,
1=+55%,
故选:D.
3.【答案】 A
【解答】 解:把y=﹣2代入方程,
得:﹣1=,
解得:a=﹣50.
则a的值为﹣50.
故选:A.
4.【答案】 B
【解答】 解:把x=5代入方程,得3+▲=10,
解得:▲=7.
故选:B.
5.【答案】 B
【解答】 解:将方程﹣=1去分母得到2(2x﹣1)﹣3x+1=6错在去分母时分子部分没有加括号,
正确结果应为2(2x﹣1)﹣3(x+1)=6.
故选:B.
6.【答案】 A
【解答】 解:设盈利服装的进价为x元,亏损服装的进价为y元,
依题意得:200﹣x=25%x,200﹣y=﹣20%y,
解得:x=160,y=250,
∴200+200﹣160﹣250=﹣10(元),
即商店在这次交易中亏了10元钱.
故选:A.
7.【答案】 B
【解答】 解:设该玻璃密封容器的容积为V,
π×a2×h=V﹣π×a2×(h﹣h),
解得V=,
故选:B.
8.【答案】 C
【解答】 解:方程(k﹣2019)x﹣2017=7﹣2019(x+1)整理化简,可得
kx=5,即x=,
∵该方程的解是整数,k为整数,
∴x=1或﹣1或5或﹣5,
即=1或﹣1或5或﹣5,
解得:k=5或﹣5或1或﹣1,
∴整数k的取值个数是4个,
故选:C.
二、填空题(共8小题)
9.【答案】 ①③⑤
【解答】 解:x﹣1=3是一元一次方程;
2x﹣y=5是二元一次方程;
﹣y=﹣2是一元一次方程;
x+3﹣4x为多项式,不是方程;
x=0是一元一次方程.
故答案为①③⑤.
10.【答案】 x
26+2
+3=
x
26-2
【解答】 解:设A港与B港相距xkm,
根据题意得:.
故答案是:.
11.【答案】 x=4
【解答】 解:∵王涵同学在解关于x的方程7a+x=18时,误将+x看作﹣x,得方程的解为x=﹣4,
∴把x=﹣4代入方程7a﹣x=18得:7a+4=18,
解得:a=2,
即方程为14+x=18,
解得:x=4,
故答案为:x=4.
12.【答案】 35
8
【解答】 解:设壶中原有x升酒,
根据题意得:2[2(2x﹣5)﹣5]=5,
解得:x=.
答:壶中原有升酒.
故答案为:.
13.【答案】 4
【解答】 解:根据题意可得:2×5﹣4(1﹣x)=22,
10﹣4+4x=22,
4x=22﹣10+4,
4x=16,
x=4,
故答案为:4.
14.【答案】 100
【解答】 解:设这件商品的进价为x元,
由题意得140×80%﹣x=12%x,
解得x=100,
答:这件商品的进价为100元.
故答案为100.
15.【答案】 AB
【解答】 解:∵甲的速度是乙的速度的3倍,
∴甲、乙第1次相遇时,乙走了正方形周长的×=,
∴甲、乙第1次相遇在边CD上.
∵甲的速度是乙的速度的3倍,甲点依顺时针方向环行,乙点依逆时针方向环行,
∴甲、乙第2次相遇在边AD上,甲、乙第3次相遇在边AB上,甲、乙第4次相遇在边BC上,甲、乙第5次相遇在边CD上,…,
∴甲、乙相遇位置每四次一循环.
∵2019=504×4+3,
∴甲、乙第2019次相遇在边AB上.
故答案是:AB.
16.【答案】 10
【解答】 解:设增加10人再完成剩余的为x天,根据题意列方程得:
(5+10)x=3×5×5,
解得:x=5,
5+5=10(天).
故答案为:10.
三、解答题(共10小题)
17.【解答】 解:(1)去括号得:1﹣4x﹣6=﹣6x﹣3,
移项合并得:2x=2,
解得:x=1;
(2)去分母得:8x+4﹣5x+7=10,
移项合并得:3x=﹣1,
解得:x=﹣.
18.【解答】 解:(1)去括号得:2x+2=1﹣x﹣3,
移项合并得:3x=﹣4,
解得:x=﹣;
(2)去分母得:10x﹣14+12=9x﹣3,
移项合并得:x=﹣1.
19.【解答】 解:(1)3x﹣7(x﹣1)=3﹣2(x+3),
去括号,得3x﹣7x+7=3﹣2x﹣6,
移项,得3x﹣7x+2x=3﹣6﹣7,
合并同类项,得﹣2x=﹣10,
系数化为1,得x=5;
(2)﹣=1+,
去分母,得(x﹣2)﹣2(x+2)=6+3(x﹣1),
去括号,得x﹣2﹣2x﹣4=6+3x﹣3,
移项,合并同类项,得﹣4x=9,
系数化为1,得x=.
20.【解答】 解:设甲组加工机器零件x件,那么乙组加工机器零件(180﹣x)件,
根据题意得:,
解得:x=60,
∴180﹣x=120,
答:设甲组加工机器零件60件,那么乙组加工机器零件120件.
21.【解答】 解:(1)由题意,得 64a+126a=950,
解得:a=5,
答:a的值为5.
(2)①设纸盒装共包装了x箱,则编织袋装共包装y 袋,
由题意,得,
解得:
答:纸盒装共包装了35箱.
②由8x+18y=1000,可得 ,
由题意得,64×(125﹣﹣b)+126y=7280,
解得:y=40﹣,
∵x,y,b都是整数,且x≥0,y≥0,b>0,
∴b=9,x=107,y=8,
∴b的值为9.
答:b的值为9.
22.【答案】 【第1空】(40x+3200)
【第2空】(36x+3600)
【第3空】100
【解答】 解:(1)①20×200+(x﹣20)×40
=(40x+3200)元;
②20×200×90%+40×90%x
=(36x+3600)元;
故答案为①(40x+3200);②(36x+3600);
(2)①当x=30元时,40x+3200=40×30+3200=4400(元);
36x+3600=36×30+3600=4680(元),
4400<4680,
故当x=30时,按方案一购买比较合算;
②由题意得40x+3200=36x+3600,
解得x=100,
但:当x=100条时,两种购买方案付款相同.
故答案为100.
23.【解答】 解:(1)点P所走过的路程表示为:AP=2t,
当t=1时,AP=2.
因为点A表示的有理数为﹣6.
所以,点P表示的有理数为﹣4;
(2)AB=10,
由题意得:2t=10.
解得:t=5.
所以,5秒时点P与点B重合;
(3)在点P由点A到点B的运动过程中,PA=2t,
在点P由点B到点A的运动过程中,PA=20﹣2t,
(4)在点P由点A到点B的运动过程中,PA=2t.
在点P由点B到点A的运动过程中,PB=2t﹣10.
在点P由点A到点B的运动过程中,2t=4,或2t=8,
解得t=2或t=4;
在点P由点B到点A的运动过程中,2t﹣10=2或2t﹣10=6,
解得t=6或t=8;
综上:满足条件的t=2,t=4,t=6,t=8.
24.【答案】 4
【解答】 解:(1)根据题中的新定义得:原式=2+6×=2+2=4;
故答案为:4;
(2)由题意得:﹣=1,
去分母,得:3x﹣5(x﹣3)=15,
去括号,得:3x﹣5x+15=15,
移项及合并,得:﹣2x=0,
系数化为1,得:x=0.
25.【解答】 解:(1)同一行中的第一个数为:a﹣1.
第三个数为:a+1;
(2)同一列中的第一个数为:a﹣7.第三个数为:a+7.
(3)设9个数中间的数为:x,则这九个数分别为:
x+8,x+7,x+6,x﹣1,x,x+1,x﹣8,x﹣7,x﹣6,
则这9个数的和为:(x+8)+(x+7)+( x+6)+( x﹣1)+(x+1)+x+(x﹣8)+(x﹣7)+(x﹣6)=9x.
所以:当9个数的和为207时,即:9x=207
解得:x=23.
所以:此时的九个数分别是:
15 16 17
22 23 24
29 30 31.
26.【解答】 解:(1)该户型商品房的面积为:4×7+3×4+2×4+2x=48+2x(平方米).
方案一购买一套该户型商品房的总金额为:(4×7+3×4+×2×4+2x)×5000=220000+10000x(元).
方案二购买一套该户型商品房的总金额为:(4×7+3×4+2×4+2x)×5000×95%=228000+9500x(元).
(2)当x=2时,方案一总金额为:220000+10000x=240000(元)
方案二总金额为:228000+9500x=247000(元)
方案一比方案二优惠7000元.
(3)根据题意得:李老师在借款后第n(1≤n≤120,n是正整数)个月的还款数额为:1500+[180000﹣1500(n﹣1)]×0.5%=2407.5﹣7.5n(元).
学校:________ 班级:________ 姓名:________ 学号:________
一、单选题(共8小题)
1.七年级学生人数为x,其中男生占52%,女生有150人,下列正确的是( )
A.1﹣52%x=150 B.x=150﹣52%x
C.(1+52%)x=150 D.(1﹣52%)x=150
2.“某学校七年级学生人数为n,其中男生占55%,女生共有110人.”下列方程能表示上述语句中的相等关系的有( )
①(1﹣55%)n=110;②1﹣55%=;③55%=1﹣;④n=;⑤1=+55%.
A.2个 B.3个 C.4个 D.5个
3.若关于y的一元一次方程的解是y=﹣2,则a的值是( )
A.﹣50 B.﹣40 C.40 D.50
4.若方程3+▲=2x的解为x=5,则▲=( )
A.9 B.7 C.5 D.4
5.将方程﹣=1去分母得到2(2x﹣1)﹣3x+1=6错在( )
A.最简公分母找错
B.去分母时分子部分没有加括号
C.去分母时漏乘3项
D.去分母时各项所乘的数不同
6.某商店在某一时间以200元的价格卖出两件衣服,其中一件盈利25%,另一件亏损20%,那么商店在这次交易中( )
A.亏了10元钱 B.亏了20元钱 C.盈利20元钱 D.不赢不亏
7.有一个不完整圆柱形玻璃密封容器如图①,测得其底面半径为a,高为h,其内装蓝色液体若干.若如图②放置时,测得液面高为h;若如图3放置时,测得液面高为h.则该玻璃密封容器的容积(圆柱体容积=底面积×高)是( )
A. B. C. D.
8.若关于x的方程(k﹣2019)x﹣2017=7﹣2019(x+1)的解是整数,则整数k的取值个数是( )
A.2 B.3 C.4 D.6
二、填空题(共8小题)
9.下列各式中,化简后是一元一次方程的是 .
①x﹣1=3;②2x﹣y=5;③﹣y=﹣2;④x+3﹣4x;⑤x=0.
10.轮船沿江从A港顺流行驶到B港,比从B港返回少用3h.若船速为26km/h,水速为2km/h,设A港和B港相距xkm,列方程得: .
11.王涵同学在解关于x的方程7a+x=18时,误将+x看作﹣x,得方程的解为x=﹣4,那么原方程的解为 .
12.《算法统宗》中记有“李白沽酒”的故事.诗云:今携一壶酒,游春郊外走.逢朋加一倍,入店饮半斗.相逢三处店,饮尽壶中酒.试问能算士:如何知原有?(古代一斗是10升)
大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的5升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.则李白的酒壶中原有 升酒.
13.a,b,c,d为有理数,现规定一种运算:=ad﹣bc,那么当=22时x的值是 .
14.一件商品标价140元,若八折出售,仍可获利12%,则这件商品的进价为 元.
15.如图,甲、乙两个动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点按顺时针方向环形运动,乙点按逆时针方向环形运动.若甲的速度是乙的速度的3倍.则它们第2019次相遇在边 上.
16.5个人用5天完成了某项工程的,如果再增加工作效率相同的10个人,那么完成这项工作前后共用 天.
三、解答题(共10小题)
17.解方程:
(1)1﹣2(2x+3)=﹣3(2x+1);
(2)﹣=1.
18.解方程:
(1)2(x+1)=1﹣(x+3).
(2)+1=.
19.解方程:
(1)3x﹣7(x﹣1)=3﹣2(x+3);
(2)﹣=1+.
20.现有180件机器零件需加工,任务由甲、乙两个小组合作完成,甲先加工,乙后加工,甲组每天加工12件,乙组每天加工8件,结果共用20天完成任务.求甲、乙两组分别加工机器零件多少个.
21.温州苍南马站四季柚,声名远播,今年又是一个丰收年.某经销商为了打开销路,对1000个四季柚进行打包优惠出售.打包方式及售价如图.假设用这两种打包方式恰装完全部柚子.
(1)若销售a箱纸盒装和a袋编织袋装四季柚的收入共950元,求a的值.
(2)当销售总收入为7280元时.
①若这批四季柚全部售完,请问纸盒装共包装了多少箱,编织袋共包装了多少袋?
②若该经销商留下b(b>0)箱纸盒装送人,其余纸盒全部售出,求b的值.
22.某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
方案一:买一套西装赠送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)①若该用户按方案一购买,需付款 元(用含x的式子表示);
②若该用户按方案二购买,需付款 元(用含x的式子表示);
(2)①若x=30,通过计算说明此时按哪种方案购买比较合算?
②当x= 时,两种购买方案付款相同.
23.如图,在数轴上点A表示的有理数为﹣6,点B表示的有理数为4,点P从点A出发以每秒2个单位长度的速度在数轴上由点A到点B方向运动,当点P到达点B后立即返回,仍然以2个单位长度的速度运动至点A停止运动,设运动时间为t(单位:秒)
(1)求t=1时点P表示的有理数;
(2)求点P与点B重合时的t值;
(3)在点P由点A到点B的运动过程中,求点P与点A的距离(用含t的代数式表示);在点P由点B到点A的运动过程中,求点P与点A的距离(用含t的代数式表示);
(4)当点P表示的有理数与原点的距离是2个单位长度时,直接写出所有满足条件的t值.
24.阅读下列材料:
现规定一种运算:=ad﹣bc.
例如:=1×4﹣2×3=4﹣6=﹣2;=4x﹣(﹣2)×3=4x+6.
按照这种规定的运算,请解答下列问题:
(1)= (只填结果);
(2)已知:=1.求x的值.(写出解题过程)
25.如图:是某月份的月历表,请你认真观察月历表,回答以下问题:
(1)如果圈出同一行的三个数,用a表示中间的数,则第一个数,第三个数怎样表示?
(2)如果圈出同一列的三个数,用a表示中间的数,则第一个数,第三个数怎样表示?
(3)如果圈出如图所示的任意9个数,这9个数的和可能是207吗?如果可能,请求出这9个数;如果不可能,请说明理由.
26.李老师准备购买一套小户型商品房,他去售楼处了解情况得知.该户型商品房的单价是5000元/m2,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李老师提供了以下两种优惠方案:
方案一:整套房的单价为5000元/m2,其中厨房可免费赠送一半的面积;
方案二:整套房按原销售总金额的9.5折出售.
(1)用含x的代数式表示该户型商品房的面积及方案一、方案二中购买一套该户型商品房的总金额;
(2)当x=2时,通过计算说明哪种方案更优惠?优惠多少元?
(3)李老师因现金不够,于2019年10月在建行借了18万元住房贷款,贷款期限为10年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月应还的贷款本金数额为1500元(每月还款数额=每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率),假设贷款月利率不变,请求出李老师在借款后第n(1≤n≤120,n是正整数)个月的还款数额.(用n的代数式表示)
一元一次=方程单元测试题
参考答案
一、单选题(共8小题)
1.【答案】 D
【解答】 解:由题意得:(1﹣52%)x=150,
故选:D.
2.【答案】 D
【解答】 解:男生人数为(n﹣110),
∴55%n=n﹣110,
∴(1﹣55%)n=110,
1﹣55%=,
55%=1﹣,
1=+55%,
故选:D.
3.【答案】 A
【解答】 解:把y=﹣2代入方程,
得:﹣1=,
解得:a=﹣50.
则a的值为﹣50.
故选:A.
4.【答案】 B
【解答】 解:把x=5代入方程,得3+▲=10,
解得:▲=7.
故选:B.
5.【答案】 B
【解答】 解:将方程﹣=1去分母得到2(2x﹣1)﹣3x+1=6错在去分母时分子部分没有加括号,
正确结果应为2(2x﹣1)﹣3(x+1)=6.
故选:B.
6.【答案】 A
【解答】 解:设盈利服装的进价为x元,亏损服装的进价为y元,
依题意得:200﹣x=25%x,200﹣y=﹣20%y,
解得:x=160,y=250,
∴200+200﹣160﹣250=﹣10(元),
即商店在这次交易中亏了10元钱.
故选:A.
7.【答案】 B
【解答】 解:设该玻璃密封容器的容积为V,
π×a2×h=V﹣π×a2×(h﹣h),
解得V=,
故选:B.
8.【答案】 C
【解答】 解:方程(k﹣2019)x﹣2017=7﹣2019(x+1)整理化简,可得
kx=5,即x=,
∵该方程的解是整数,k为整数,
∴x=1或﹣1或5或﹣5,
即=1或﹣1或5或﹣5,
解得:k=5或﹣5或1或﹣1,
∴整数k的取值个数是4个,
故选:C.
二、填空题(共8小题)
9.【答案】 ①③⑤
【解答】 解:x﹣1=3是一元一次方程;
2x﹣y=5是二元一次方程;
﹣y=﹣2是一元一次方程;
x+3﹣4x为多项式,不是方程;
x=0是一元一次方程.
故答案为①③⑤.
10.【答案】 x
26+2
+3=
x
26-2
【解答】 解:设A港与B港相距xkm,
根据题意得:.
故答案是:.
11.【答案】 x=4
【解答】 解:∵王涵同学在解关于x的方程7a+x=18时,误将+x看作﹣x,得方程的解为x=﹣4,
∴把x=﹣4代入方程7a﹣x=18得:7a+4=18,
解得:a=2,
即方程为14+x=18,
解得:x=4,
故答案为:x=4.
12.【答案】 35
8
【解答】 解:设壶中原有x升酒,
根据题意得:2[2(2x﹣5)﹣5]=5,
解得:x=.
答:壶中原有升酒.
故答案为:.
13.【答案】 4
【解答】 解:根据题意可得:2×5﹣4(1﹣x)=22,
10﹣4+4x=22,
4x=22﹣10+4,
4x=16,
x=4,
故答案为:4.
14.【答案】 100
【解答】 解:设这件商品的进价为x元,
由题意得140×80%﹣x=12%x,
解得x=100,
答:这件商品的进价为100元.
故答案为100.
15.【答案】 AB
【解答】 解:∵甲的速度是乙的速度的3倍,
∴甲、乙第1次相遇时,乙走了正方形周长的×=,
∴甲、乙第1次相遇在边CD上.
∵甲的速度是乙的速度的3倍,甲点依顺时针方向环行,乙点依逆时针方向环行,
∴甲、乙第2次相遇在边AD上,甲、乙第3次相遇在边AB上,甲、乙第4次相遇在边BC上,甲、乙第5次相遇在边CD上,…,
∴甲、乙相遇位置每四次一循环.
∵2019=504×4+3,
∴甲、乙第2019次相遇在边AB上.
故答案是:AB.
16.【答案】 10
【解答】 解:设增加10人再完成剩余的为x天,根据题意列方程得:
(5+10)x=3×5×5,
解得:x=5,
5+5=10(天).
故答案为:10.
三、解答题(共10小题)
17.【解答】 解:(1)去括号得:1﹣4x﹣6=﹣6x﹣3,
移项合并得:2x=2,
解得:x=1;
(2)去分母得:8x+4﹣5x+7=10,
移项合并得:3x=﹣1,
解得:x=﹣.
18.【解答】 解:(1)去括号得:2x+2=1﹣x﹣3,
移项合并得:3x=﹣4,
解得:x=﹣;
(2)去分母得:10x﹣14+12=9x﹣3,
移项合并得:x=﹣1.
19.【解答】 解:(1)3x﹣7(x﹣1)=3﹣2(x+3),
去括号,得3x﹣7x+7=3﹣2x﹣6,
移项,得3x﹣7x+2x=3﹣6﹣7,
合并同类项,得﹣2x=﹣10,
系数化为1,得x=5;
(2)﹣=1+,
去分母,得(x﹣2)﹣2(x+2)=6+3(x﹣1),
去括号,得x﹣2﹣2x﹣4=6+3x﹣3,
移项,合并同类项,得﹣4x=9,
系数化为1,得x=.
20.【解答】 解:设甲组加工机器零件x件,那么乙组加工机器零件(180﹣x)件,
根据题意得:,
解得:x=60,
∴180﹣x=120,
答:设甲组加工机器零件60件,那么乙组加工机器零件120件.
21.【解答】 解:(1)由题意,得 64a+126a=950,
解得:a=5,
答:a的值为5.
(2)①设纸盒装共包装了x箱,则编织袋装共包装y 袋,
由题意,得,
解得:
答:纸盒装共包装了35箱.
②由8x+18y=1000,可得 ,
由题意得,64×(125﹣﹣b)+126y=7280,
解得:y=40﹣,
∵x,y,b都是整数,且x≥0,y≥0,b>0,
∴b=9,x=107,y=8,
∴b的值为9.
答:b的值为9.
22.【答案】 【第1空】(40x+3200)
【第2空】(36x+3600)
【第3空】100
【解答】 解:(1)①20×200+(x﹣20)×40
=(40x+3200)元;
②20×200×90%+40×90%x
=(36x+3600)元;
故答案为①(40x+3200);②(36x+3600);
(2)①当x=30元时,40x+3200=40×30+3200=4400(元);
36x+3600=36×30+3600=4680(元),
4400<4680,
故当x=30时,按方案一购买比较合算;
②由题意得40x+3200=36x+3600,
解得x=100,
但:当x=100条时,两种购买方案付款相同.
故答案为100.
23.【解答】 解:(1)点P所走过的路程表示为:AP=2t,
当t=1时,AP=2.
因为点A表示的有理数为﹣6.
所以,点P表示的有理数为﹣4;
(2)AB=10,
由题意得:2t=10.
解得:t=5.
所以,5秒时点P与点B重合;
(3)在点P由点A到点B的运动过程中,PA=2t,
在点P由点B到点A的运动过程中,PA=20﹣2t,
(4)在点P由点A到点B的运动过程中,PA=2t.
在点P由点B到点A的运动过程中,PB=2t﹣10.
在点P由点A到点B的运动过程中,2t=4,或2t=8,
解得t=2或t=4;
在点P由点B到点A的运动过程中,2t﹣10=2或2t﹣10=6,
解得t=6或t=8;
综上:满足条件的t=2,t=4,t=6,t=8.
24.【答案】 4
【解答】 解:(1)根据题中的新定义得:原式=2+6×=2+2=4;
故答案为:4;
(2)由题意得:﹣=1,
去分母,得:3x﹣5(x﹣3)=15,
去括号,得:3x﹣5x+15=15,
移项及合并,得:﹣2x=0,
系数化为1,得:x=0.
25.【解答】 解:(1)同一行中的第一个数为:a﹣1.
第三个数为:a+1;
(2)同一列中的第一个数为:a﹣7.第三个数为:a+7.
(3)设9个数中间的数为:x,则这九个数分别为:
x+8,x+7,x+6,x﹣1,x,x+1,x﹣8,x﹣7,x﹣6,
则这9个数的和为:(x+8)+(x+7)+( x+6)+( x﹣1)+(x+1)+x+(x﹣8)+(x﹣7)+(x﹣6)=9x.
所以:当9个数的和为207时,即:9x=207
解得:x=23.
所以:此时的九个数分别是:
15 16 17
22 23 24
29 30 31.
26.【解答】 解:(1)该户型商品房的面积为:4×7+3×4+2×4+2x=48+2x(平方米).
方案一购买一套该户型商品房的总金额为:(4×7+3×4+×2×4+2x)×5000=220000+10000x(元).
方案二购买一套该户型商品房的总金额为:(4×7+3×4+2×4+2x)×5000×95%=228000+9500x(元).
(2)当x=2时,方案一总金额为:220000+10000x=240000(元)
方案二总金额为:228000+9500x=247000(元)
方案一比方案二优惠7000元.
(3)根据题意得:李老师在借款后第n(1≤n≤120,n是正整数)个月的还款数额为:1500+[180000﹣1500(n﹣1)]×0.5%=2407.5﹣7.5n(元).
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
