2.4第3课时圆的内接四边形练习题 2021-2022学年苏科版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.4第3课时圆的内接四边形练习题 2021-2022学年苏科版九年级数学上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 227.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 08:54:14 | ||
图片预览

文档简介
第3课时 圆的内接四边形
【基础练习】
知识点 圆内接四边形的性质
1.[2020·吉林] 如图,四边形ABCD内接于☉O,若∠B=108°,则∠D的度数为 ( )
A.54° B.62° C.72° D.82°
2.如图,四边形ABCD是圆内接四边形,E是BC延长线上的一点.若∠BAD=105°,则∠DCE的度数是( )
A.115° B.105° C.100° D.95°
3.在圆内接四边形ABCD中,若∠A∶∠B∶∠C=2∶3∶4,则∠D的度数是 ( )
A.60° B.90° C.120° D.30°
4.[2020·牡丹江] 如图1,四边形ABCD内接于☉O,连接BD.若AC=BC,∠BDC=50°,则∠ADC的度数是( )
图1
A.125° B.130° C.135° D.140°
5.如图2,四边形ABCD内接于☉O.若四边形ABCO是平行四边形,则∠ADC的度数为
( )
图2
A.45° B.50° C.60° D.75°
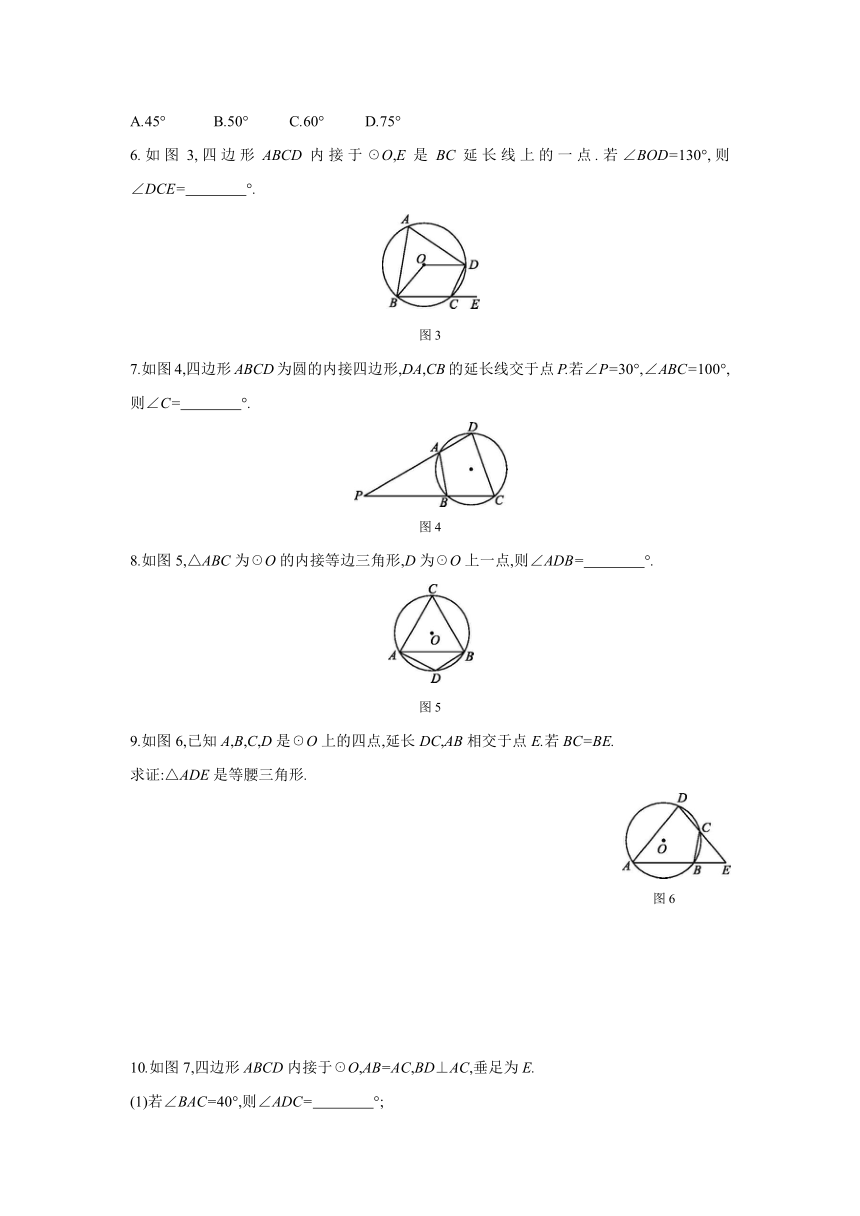
6.如图3,四边形ABCD内接于☉O,E是BC延长线上的一点.若∠BOD=130°,则∠DCE= °.?
图3
7.如图4,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P.若∠P=30°,∠ABC=100°,则∠C= °.?
图4
8.如图5,△ABC为☉O的内接等边三角形,D为☉O上一点,则∠ADB= °.?
图5
9.如图6,已知A,B,C,D是☉O上的四点,延长DC,AB相交于点E.若BC=BE.
求证:△ADE是等腰三角形.
图6
10.如图7,四边形ABCD内接于☉O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC= °;?
(2)求证:∠BAC=2∠DAC.
图7
【能力提升】
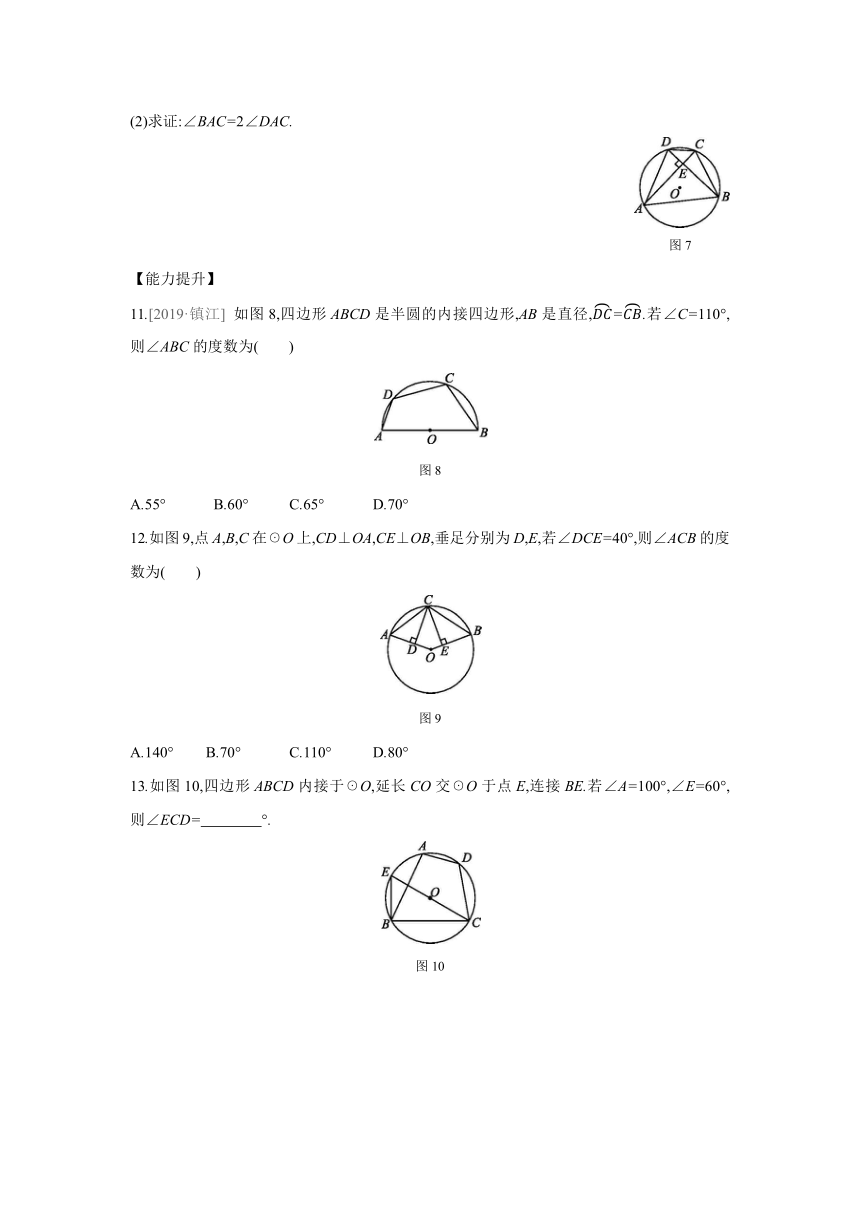
11.[2019·镇江] 如图8,四边形ABCD是半圆的内接四边形,AB是直径,DC=CB.若∠C=110°,则∠ABC的度数为( )
图8
A.55° B.60° C.65° D.70°
12.如图9,点A,B,C在☉O上,CD⊥OA,CE⊥OB,垂足分别为D,E,若∠DCE=40°,则∠ACB的度数为( )
图9
A.140° B.70° C.110° D.80°
13.如图10,四边形ABCD内接于☉O,延长CO交☉O于点E,连接BE.若∠A=100°,∠E=60°,则∠ECD= °.
图10
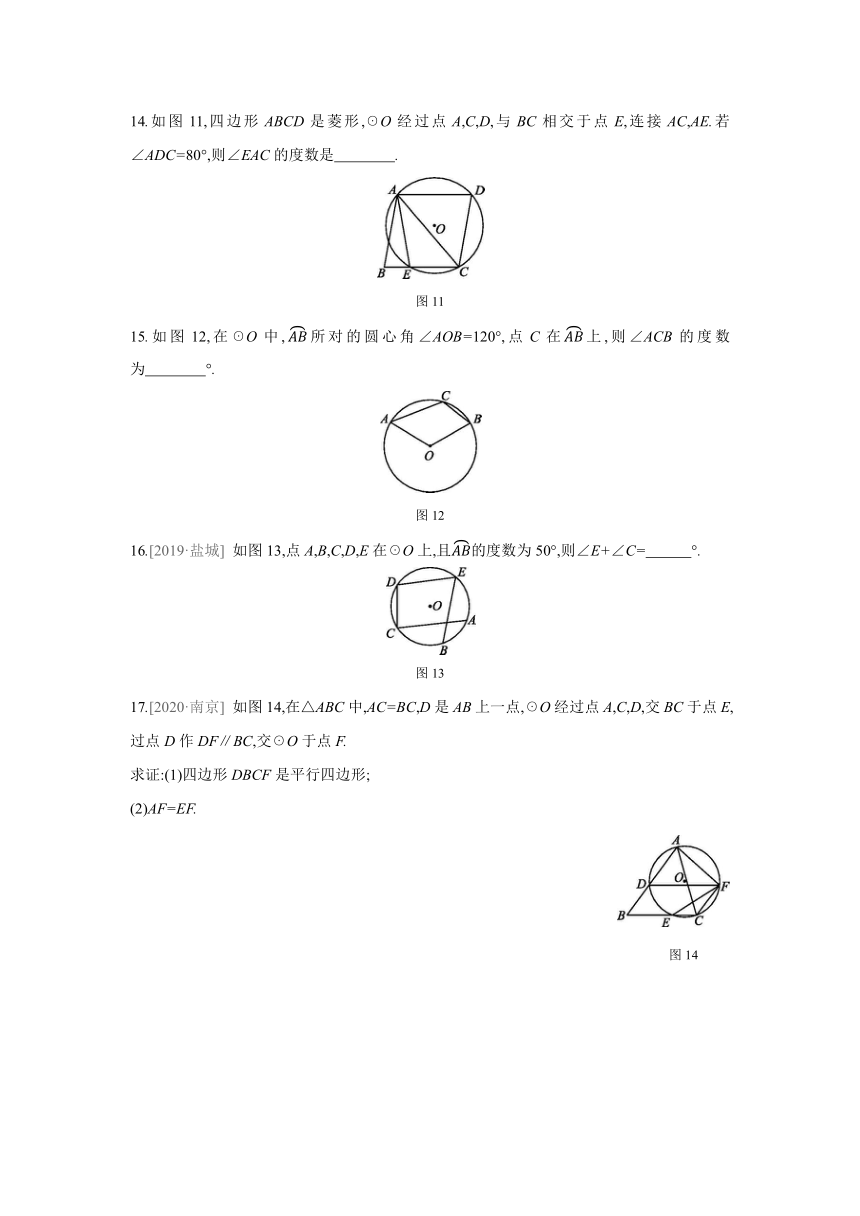
14.如图11,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠ADC=80°,则∠EAC的度数是 .?
图11
15.如图12,在☉O中,AB所对的圆心角∠AOB=120°,点C在AB上,则∠ACB的度数为 °.?
图12
16.[2019·盐城] 如图13,点A,B,C,D,E在☉O上,且AB的度数为50°,则∠E+∠C= °.?
图13
17.[2020·南京] 如图14,在△ABC中,AC=BC,D是AB上一点,☉O经过点A,C,D,交BC于点E,过点D作DF∥BC,交☉O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
图14
18.如图15,☉O的内接四边形ABCD两组对边的延长线分别相交于点E,F.
(1)若∠E=∠F,求证:∠ADC=∠ABC;
(2)若∠E=∠F=42°,求∠A的度数;
(3)若∠E=α,∠F=β,且α≠β,请你用含有α,β的代数式表示∠A的度数.
图15
答案
1.C [解析] ∵四边形ABCD内接于☉O,∠B=108°,∴∠D=180°-∠B=180°-108°=72°.故选C.
2.B [解析] ∵四边形ABCD是圆内接四边形,∴∠BAD+∠BCD=180°.
又∵∠BCD+∠DCE=180°,∴∠DCE=∠BAD.而∠BAD=105°,∴∠DCE=105°.故选B.
3.B [解析] ∵∠A∶∠B∶∠C=2∶3∶4,∴设∠A=2x,则∠B=3x,∠C=4x.
∵四边形ABCD为圆内接四边形,∴∠A+∠C=180°,即2x+4x=180°,解得x=30°,
∴∠B=3x=90°,∴∠D=180°-∠B=180°-90°=90°.故选B.
4.B [解析] ∵AC=BC,∴∠ABC=∠BDC=50°,∴∠ADC=180°-∠ABC=130°.故选B.
5.C
6.65
7.70 [解析] ∵∠ABC=100°,∠P=30°,∴∠PAB=∠ABC-∠P=70°.∵四边形ABCD为圆的内接四边形,∴∠C+∠BAD=180°.∵∠BAD+∠PAB=180°,∴∠C=∠PAB=70°.
8.120 [解析] ∵△ABC为☉O的内接等边三角形,∴∠C=60°.又∵四边形ACBD是☉O的内接四边形,∴∠C+∠ADB=180°.∴∠ADB=180°-60°=120°.
9.证明:∵A,B,C,D是☉O上的四点,∴四边形ABCD是☉O的内接四边形,
∴∠A+∠DCB=180°.又∵∠BCE+∠DCB=180°,∴∠A=∠BCE.
∵BC=BE,∴∠BCE=∠E,∴∠A=∠E,∴AD=DE,即△ADE是等腰三角形.
10.解:(1)∵AB=AC,∠BAC=40°,∴∠ABC=∠ACB=70°.∵四边形ABCD是☉O的内接四边形,∴∠ADC=180°-∠ABC=110°.故答案为110.
(2)证明:∵BD⊥AC,∴∠BEC=90°,∴∠ACB=90°-∠CBD.∵AB=AC,
∴∠ABC=∠ACB=90°-∠CBD,∴∠BAC=180°-2∠ABC=2∠CBD.
又∵∠DAC=∠CBD,∴∠BAC=2∠DAC.
403479047244011.A [解析] 如图,连接AC.∵四边形ABCD是半圆的内接四边形,
∴∠DAB=180°-∠DCB=70°.∵DC=CB,∴∠CAB=12∠DAB=35°.
∵AB是半圆O的直径,∴∠ACB=90°,∴∠ABC=90°-∠CAB=55°.
12.C [解析] 如图,在优弧AB上取一点P,连接AP,BP.∵CD⊥OA,CE⊥OB,
2232025647700∴∠ODC=∠OEC=90°.∵∠DCE=40°,∴∠AOB=360°-90°-90°-40°=140°,∴∠P=12∠AOB=70°.∵A,C,B,P四点共圆,∴∠P+∠ACB=180°,∴∠ACB=180°-70°=110°.故选C.
13.50 [解析] ∵EC是☉O的直径,∴∠EBC=90°.又∵∠E=60°,∴∠BCE=30°.
∵四边形ABCD内接于☉O,∴∠BCD=180°-∠A=80°.∴∠ECD=∠BCD-∠BCE=50°.
14.30° [解析] ∵四边形ABCD是菱形,∠D=80°,∴∠ACB=12∠DCB=12(180°-∠D)=50°.∵四边形AECD是圆内接四边形,∴∠AEB=∠D=80°,∴∠EAC=∠AEB-∠ACE=30°.
15.120 [解析] 如图,在优弧AB上取一点D,连接AD,BD.∵∠AOB=120°,
∴∠ADB=12∠AOB=12×120°=60°,∴∠ACB=180°-∠ADB=180°-60°=120°.
16.155 [解析] 如图,连接EA.∵AB的度数为50°,∴∠BEA=25°.∵四边形DCAE为☉O的内接四边形,∴∠DEA+∠C=180°.∴∠DEB+∠C=180°-25°=155°.
17.证明:(1)∵AC=BC,∴∠BAC=∠B.∵DF∥BC,∴∠ADF=∠B.∵∠BAC=∠CFD,
∴∠ADF=∠CFD,∴BD∥CF.又∵DF∥BC,∴四边形DBCF是平行四边形.
(2)如图,连接AE.
∵∠ADF=∠B,∠ADF=∠AEF,∴∠AEF=∠B.∵四边形AECF是☉O的内接四边形,
∴∠ECF+∠EAF=180°.∵BD∥CF,∴∠ECF+∠B=180°,∴∠EAF=∠B,
∴∠AEF=∠EAF,∴AF=EF.
18.解:(1)证明:∵∠E=∠F,∠ECD=∠FCB,∴∠E+∠ECD=∠F+∠FCB,
即∠ADC=∠ABC.
(2)∵∠A+∠BCD=180°,∠ECD+∠BCD=180°,∴∠A=∠ECD.
∵∠EDC=∠A+∠F,∠EDC+∠E+∠ECD=180°,
∴2∠A+∠E+∠F=180°.又∵∠E=∠F=42°,∴∠A=48°.
(3)由(2)中的结论可知2∠A+∠E+∠F=180°,
∴2∠A+α+β=180°,解得∠A=90°-12(α+β).
【基础练习】
知识点 圆内接四边形的性质
1.[2020·吉林] 如图,四边形ABCD内接于☉O,若∠B=108°,则∠D的度数为 ( )
A.54° B.62° C.72° D.82°
2.如图,四边形ABCD是圆内接四边形,E是BC延长线上的一点.若∠BAD=105°,则∠DCE的度数是( )
A.115° B.105° C.100° D.95°
3.在圆内接四边形ABCD中,若∠A∶∠B∶∠C=2∶3∶4,则∠D的度数是 ( )
A.60° B.90° C.120° D.30°
4.[2020·牡丹江] 如图1,四边形ABCD内接于☉O,连接BD.若AC=BC,∠BDC=50°,则∠ADC的度数是( )
图1
A.125° B.130° C.135° D.140°
5.如图2,四边形ABCD内接于☉O.若四边形ABCO是平行四边形,则∠ADC的度数为
( )
图2
A.45° B.50° C.60° D.75°
6.如图3,四边形ABCD内接于☉O,E是BC延长线上的一点.若∠BOD=130°,则∠DCE= °.?
图3
7.如图4,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P.若∠P=30°,∠ABC=100°,则∠C= °.?
图4
8.如图5,△ABC为☉O的内接等边三角形,D为☉O上一点,则∠ADB= °.?
图5
9.如图6,已知A,B,C,D是☉O上的四点,延长DC,AB相交于点E.若BC=BE.
求证:△ADE是等腰三角形.
图6
10.如图7,四边形ABCD内接于☉O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC= °;?
(2)求证:∠BAC=2∠DAC.
图7
【能力提升】
11.[2019·镇江] 如图8,四边形ABCD是半圆的内接四边形,AB是直径,DC=CB.若∠C=110°,则∠ABC的度数为( )
图8
A.55° B.60° C.65° D.70°
12.如图9,点A,B,C在☉O上,CD⊥OA,CE⊥OB,垂足分别为D,E,若∠DCE=40°,则∠ACB的度数为( )
图9
A.140° B.70° C.110° D.80°
13.如图10,四边形ABCD内接于☉O,延长CO交☉O于点E,连接BE.若∠A=100°,∠E=60°,则∠ECD= °.
图10
14.如图11,四边形ABCD是菱形,☉O经过点A,C,D,与BC相交于点E,连接AC,AE.若∠ADC=80°,则∠EAC的度数是 .?
图11
15.如图12,在☉O中,AB所对的圆心角∠AOB=120°,点C在AB上,则∠ACB的度数为 °.?
图12
16.[2019·盐城] 如图13,点A,B,C,D,E在☉O上,且AB的度数为50°,则∠E+∠C= °.?
图13
17.[2020·南京] 如图14,在△ABC中,AC=BC,D是AB上一点,☉O经过点A,C,D,交BC于点E,过点D作DF∥BC,交☉O于点F.
求证:(1)四边形DBCF是平行四边形;
(2)AF=EF.
图14
18.如图15,☉O的内接四边形ABCD两组对边的延长线分别相交于点E,F.
(1)若∠E=∠F,求证:∠ADC=∠ABC;
(2)若∠E=∠F=42°,求∠A的度数;
(3)若∠E=α,∠F=β,且α≠β,请你用含有α,β的代数式表示∠A的度数.
图15
答案
1.C [解析] ∵四边形ABCD内接于☉O,∠B=108°,∴∠D=180°-∠B=180°-108°=72°.故选C.
2.B [解析] ∵四边形ABCD是圆内接四边形,∴∠BAD+∠BCD=180°.
又∵∠BCD+∠DCE=180°,∴∠DCE=∠BAD.而∠BAD=105°,∴∠DCE=105°.故选B.
3.B [解析] ∵∠A∶∠B∶∠C=2∶3∶4,∴设∠A=2x,则∠B=3x,∠C=4x.
∵四边形ABCD为圆内接四边形,∴∠A+∠C=180°,即2x+4x=180°,解得x=30°,
∴∠B=3x=90°,∴∠D=180°-∠B=180°-90°=90°.故选B.
4.B [解析] ∵AC=BC,∴∠ABC=∠BDC=50°,∴∠ADC=180°-∠ABC=130°.故选B.
5.C
6.65
7.70 [解析] ∵∠ABC=100°,∠P=30°,∴∠PAB=∠ABC-∠P=70°.∵四边形ABCD为圆的内接四边形,∴∠C+∠BAD=180°.∵∠BAD+∠PAB=180°,∴∠C=∠PAB=70°.
8.120 [解析] ∵△ABC为☉O的内接等边三角形,∴∠C=60°.又∵四边形ACBD是☉O的内接四边形,∴∠C+∠ADB=180°.∴∠ADB=180°-60°=120°.
9.证明:∵A,B,C,D是☉O上的四点,∴四边形ABCD是☉O的内接四边形,
∴∠A+∠DCB=180°.又∵∠BCE+∠DCB=180°,∴∠A=∠BCE.
∵BC=BE,∴∠BCE=∠E,∴∠A=∠E,∴AD=DE,即△ADE是等腰三角形.
10.解:(1)∵AB=AC,∠BAC=40°,∴∠ABC=∠ACB=70°.∵四边形ABCD是☉O的内接四边形,∴∠ADC=180°-∠ABC=110°.故答案为110.
(2)证明:∵BD⊥AC,∴∠BEC=90°,∴∠ACB=90°-∠CBD.∵AB=AC,
∴∠ABC=∠ACB=90°-∠CBD,∴∠BAC=180°-2∠ABC=2∠CBD.
又∵∠DAC=∠CBD,∴∠BAC=2∠DAC.
403479047244011.A [解析] 如图,连接AC.∵四边形ABCD是半圆的内接四边形,
∴∠DAB=180°-∠DCB=70°.∵DC=CB,∴∠CAB=12∠DAB=35°.
∵AB是半圆O的直径,∴∠ACB=90°,∴∠ABC=90°-∠CAB=55°.
12.C [解析] 如图,在优弧AB上取一点P,连接AP,BP.∵CD⊥OA,CE⊥OB,
2232025647700∴∠ODC=∠OEC=90°.∵∠DCE=40°,∴∠AOB=360°-90°-90°-40°=140°,∴∠P=12∠AOB=70°.∵A,C,B,P四点共圆,∴∠P+∠ACB=180°,∴∠ACB=180°-70°=110°.故选C.
13.50 [解析] ∵EC是☉O的直径,∴∠EBC=90°.又∵∠E=60°,∴∠BCE=30°.
∵四边形ABCD内接于☉O,∴∠BCD=180°-∠A=80°.∴∠ECD=∠BCD-∠BCE=50°.
14.30° [解析] ∵四边形ABCD是菱形,∠D=80°,∴∠ACB=12∠DCB=12(180°-∠D)=50°.∵四边形AECD是圆内接四边形,∴∠AEB=∠D=80°,∴∠EAC=∠AEB-∠ACE=30°.
15.120 [解析] 如图,在优弧AB上取一点D,连接AD,BD.∵∠AOB=120°,
∴∠ADB=12∠AOB=12×120°=60°,∴∠ACB=180°-∠ADB=180°-60°=120°.
16.155 [解析] 如图,连接EA.∵AB的度数为50°,∴∠BEA=25°.∵四边形DCAE为☉O的内接四边形,∴∠DEA+∠C=180°.∴∠DEB+∠C=180°-25°=155°.
17.证明:(1)∵AC=BC,∴∠BAC=∠B.∵DF∥BC,∴∠ADF=∠B.∵∠BAC=∠CFD,
∴∠ADF=∠CFD,∴BD∥CF.又∵DF∥BC,∴四边形DBCF是平行四边形.
(2)如图,连接AE.
∵∠ADF=∠B,∠ADF=∠AEF,∴∠AEF=∠B.∵四边形AECF是☉O的内接四边形,
∴∠ECF+∠EAF=180°.∵BD∥CF,∴∠ECF+∠B=180°,∴∠EAF=∠B,
∴∠AEF=∠EAF,∴AF=EF.
18.解:(1)证明:∵∠E=∠F,∠ECD=∠FCB,∴∠E+∠ECD=∠F+∠FCB,
即∠ADC=∠ABC.
(2)∵∠A+∠BCD=180°,∠ECD+∠BCD=180°,∴∠A=∠ECD.
∵∠EDC=∠A+∠F,∠EDC+∠E+∠ECD=180°,
∴2∠A+∠E+∠F=180°.又∵∠E=∠F=42°,∴∠A=48°.
(3)由(2)中的结论可知2∠A+∠E+∠F=180°,
∴2∠A+α+β=180°,解得∠A=90°-12(α+β).
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
