2.4_2.5练习题 2021-2022学年苏科版九年级数学上册(Word版 含答案)
文档属性
| 名称 | 2.4_2.5练习题 2021-2022学年苏科版九年级数学上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 238.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览

文档简介
2.4~2.5练习题
一、选择题(每小题4分,共32分)
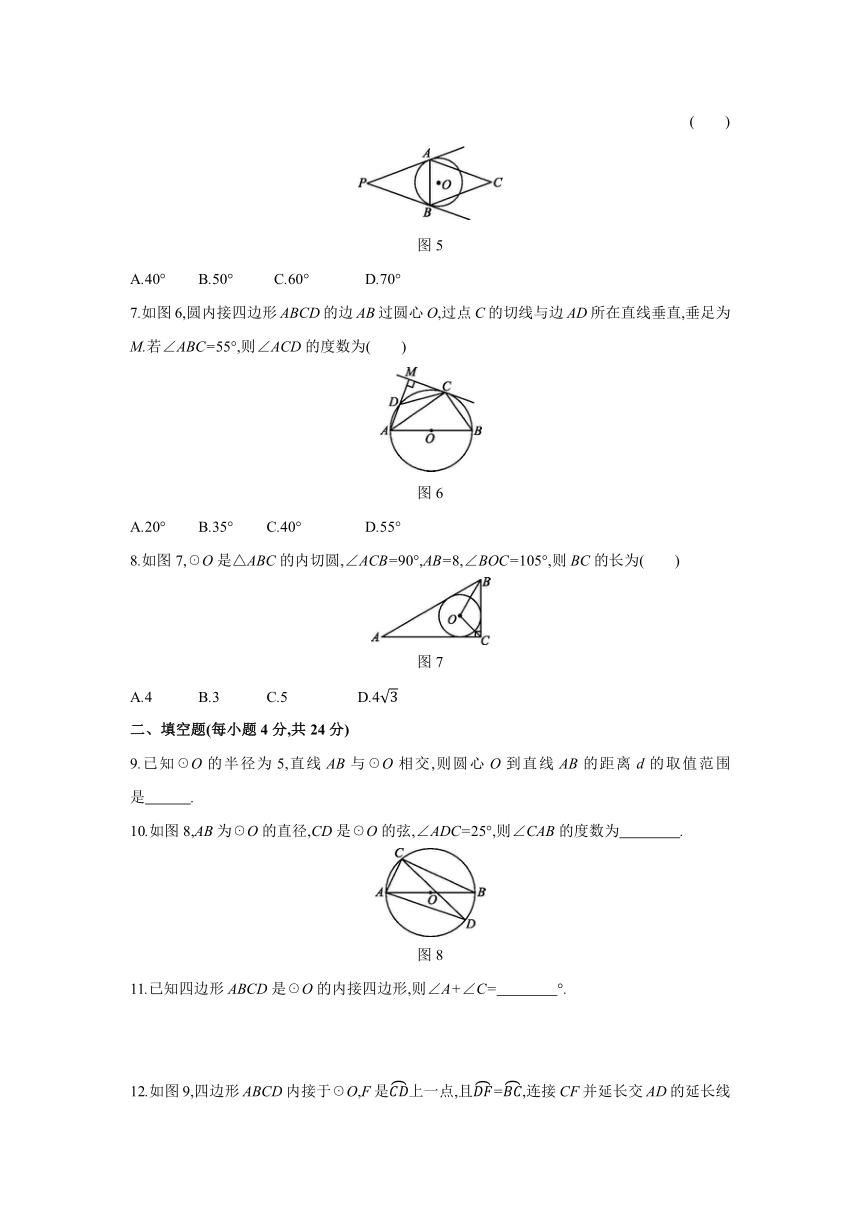
1.如图1,AB是☉O的直径,若∠BAC=20°,则∠ADC的度数为 ( )
图1
A.40° B.60° C.70° D.80°
2.若直线l与半径为r的☉O相交,且点O到直线l的距离为6,则r的取值范围是 ( )
A.r<6 B.r=6 C.r>6 D.r≥6
3.如图2,四边形ABCD为☉O的内接四边形,已知∠BCD=120°,则∠BOD的度数为
( )
图2
A.100° B.110° C.120° D.130°
27381202647954.如图3,AB是圆O的弦,OC⊥AB交圆O于点C,D是圆O上一点,∠ADC=35°,则∠BOC的度数为 ( )
A.50° B.60° C.70° D.80° 图3
5.如图4,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,BP=4,则线段AP的长为 ( )
图4
A.4 B.8 C.43 D.42
6.如图5,在?APBC中,∠C=40°.若☉O分别与PA,PB相切于点A,B,则∠CAB的度数为
( )
图5
A.40° B.50° C.60° D.70°
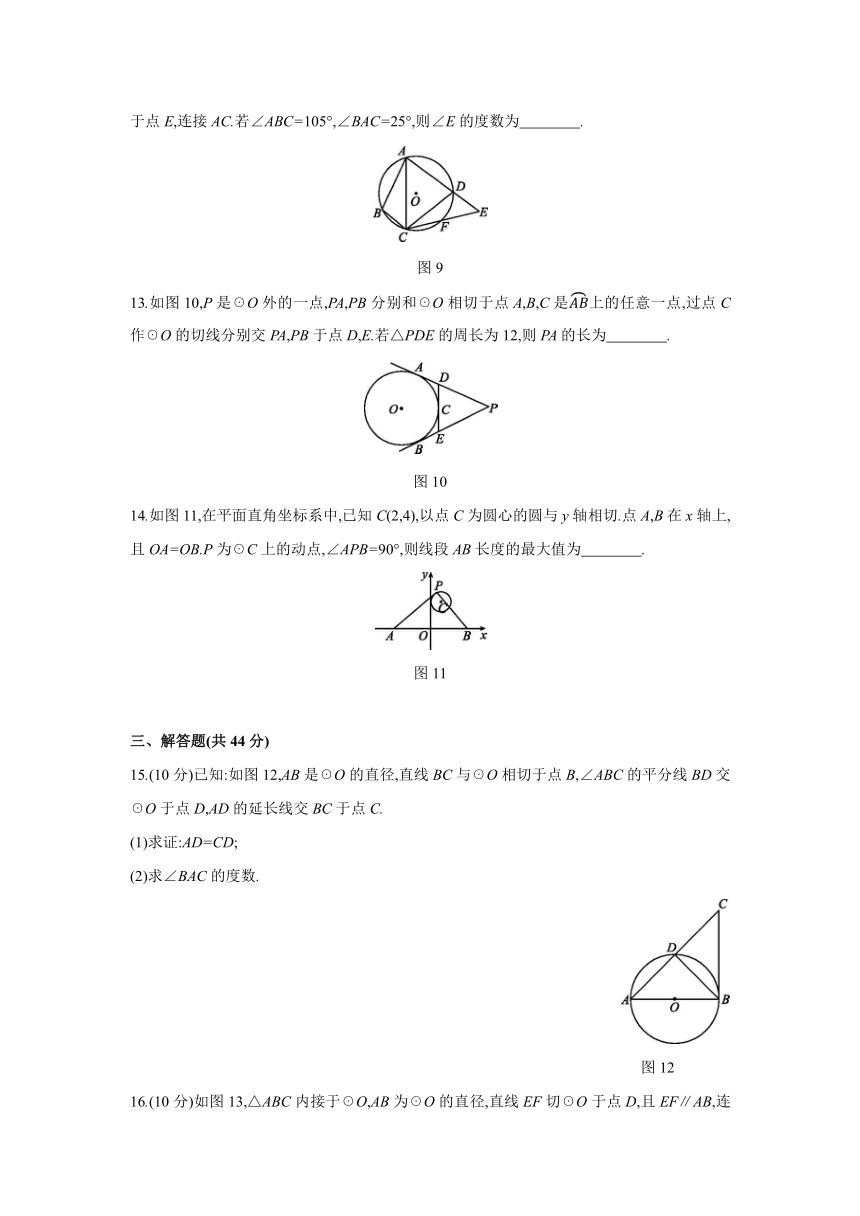
7.如图6,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直,垂足为M.若∠ABC=55°,则∠ACD的度数为( )
图6
A.20° B.35° C.40° D.55°
8.如图7,☉O是△ABC的内切圆,∠ACB=90°,AB=8,∠BOC=105°,则BC的长为( )
图7
A.4 B.3 C.5 D.43
二、填空题(每小题4分,共24分)
9.已知☉O的半径为5,直线AB与☉O相交,则圆心O到直线AB的距离d的取值范围是 .?
10.如图8,AB为☉O的直径,CD是☉O的弦,∠ADC=25°,则∠CAB的度数为 .
图8
11.已知四边形ABCD是☉O的内接四边形,则∠A+∠C= °.?
12.如图9,四边形ABCD内接于☉O,F是CD上一点,且DF=BC,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为 .?
图9
13.如图10,P是☉O外的一点,PA,PB分别和☉O相切于点A,B,C是AB上的任意一点,过点C作☉O的切线分别交PA,PB于点D,E.若△PDE的周长为12,则PA的长为 .?
图10
14.如图11,在平面直角坐标系中,已知C(2,4),以点C为圆心的圆与y轴相切.点A,B在x轴上,且OA=OB.P为☉C上的动点,∠APB=90°,则线段AB长度的最大值为 .?
图11
三、解答题(共44分)
15.(10分)已知:如图12,AB是☉O的直径,直线BC与☉O相切于点B,∠ABC的平分线BD交☉O于点D,AD的延长线交BC于点C.
(1)求证:AD=CD;
(2)求∠BAC的度数.
图12
16.(10分)如图13,△ABC内接于☉O,AB为☉O的直径,直线EF切☉O于点D,且EF∥AB,连接CD,BD.
(1)求证:CD平分∠ACB;
(2)若∠ABC=30°,BD=22,求CD的长.
图13
17.(12分)如图14,四边形ABCD 内接于☉O,BD是☉O的直径,过点A作☉O的切线AE交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE⊥CD;
(2)已知AE=4 cm,CD=6 cm,求☉O的半径.
图14
18.(12分)如图15,在四边形ABCD中,AB=AD=CD,以AB为直径的☉O经过点C,连接AC,OD交于点E.
(1)如图①,求证:OD∥BC;
(2)如图②,若AD是☉O的切线,连接BD交☉O于点F,连接EF,且OA=5,求EF的长.
图15
答案
1.C [解析] ∵AB是☉O的直径,∴∠ACB=90°.∵∠BAC=20°,∴∠ABC=90°-20°=70°,
∴∠ADC=∠ABC=70°.故选C.
2.C
3.C [解析] ∵四边形ABCD是☉O的内接四边形,∴∠A=180°-∠BCD=60°.由圆周角定理,得∠BOD=2∠A=120°.故选C.
4.C [解析] ∵OC⊥AB,∴AC=BC,∴∠AOC=∠BOC.∵∠ADC=35°,∴∠AOC=70°,
∴∠BOC=70°.故选C.
5.C [解析] 连接OA,如图所示.∵PA为☉O的切线,∴PA⊥OA,∴∠OAP=90°.∵∠P=30°,
∴OP=2OA=2OB,AP=3OA,∴OA=OB=BP=4,∴AP=43.故选C.
6.D [解析] ∵☉O分别与PA,PB相切于点A,B,∴PA=PB.∵四边形APBC是平行四边形,
∴四边形APBC是菱形,∴AC=BC.又∵∠C=40°,∴∠CAB=70°.
7.A
8.A [解析] ∵☉O是△ABC的内切圆,∴∠OBC=12∠ABC,∠OCB=12∠ACB.∵∠BOC=105°,
∴∠OBC+∠OCB=180°-105°=75°.∴∠ABC+∠ACB=2×75°=150°.∴∠A=180°-(∠ABC+∠ACB)=30°.∵∠ACB=90°,AB=8,∴BC=12AB=4.故选A.
9.0≤d<5
10.65° [解析] 由圆周角定理,得∠ABC=∠ADC=25°.∵AB为☉O的直径,∴∠ACB=90°.
∴∠CAB=90°-∠ABC=65°.
11.180
12.50° [解析] ∵四边形ABCD内接于☉O,∠ABC=105°,∴∠ADC=180°-∠ABC=180°-105°=
75°.∵DF=BC,∠BAC=25°,∴∠DCE=∠BAC=25°,∴∠E=∠ADC-∠DCE=75°-25°=50°.
13. 6 [解析] 根据切线长定理,得AD=CD,CE=BE,PA=PB,则△PDE的周长=2PA=12,
∴PA=6.
14.45+4 [解析] 连接OC并延长交☉C于点P,此时AB的长度最大.∵C(2,4),
∴OC=22+42=25.∵以点C为圆心的圆与y轴相切,∴☉C的半径为2.∵∠APB=90°,
∴OP=OA=OB=2+25,∴AB长度的最大值为45+4.
15.解:(1)证明:∵AB是☉O的直径,∴∠ADB=90°.∴∠CDB=90°.∴∠ADB=∠CDB.
∵BD平分∠ABC,∴∠ABD=∠CBD.在△ABD和△CBD中,∠ADB=∠CDB,BD=BD,∠ABD=∠CBD,
∴△ABD≌△CBD(ASA).∴AD=CD.
(2)∵△ABD≌△CBD,∴AB=CB.∵直线BC与☉O相切于点B,∴∠ABC=90°.
∴∠BAC=∠C=45°.
16.解:(1)证明:如图,连接OD.∵直线EF切☉O于点D,∴OD⊥EF.∵AB∥EF,
∴OD⊥AB,∴∠AOD=∠BOD=90°,∴AD=BD,∴∠ACD=∠BCD,∴CD平分∠ACB.
(2)由(1)知∠BOD=90°,∴OB=OD=22BD=2,∴AB=2OB=4.∵AB为☉O的直径,∴∠ACB=90°.
又∠ABC=30°,∴AC=12AB=2.如图,连接AD,作AH⊥CD于点H.∵∠ACH=12∠ACB=45°,
∴CH=AH.设CH=x.∵CH2+AH2=AC2,∴x2+x2=22,∴x=2,即AH=CH=2.
∵∠ADC=∠ABC=30°,∴AD=2AH=22,∴DH=6,∴CD=CH+DH=2+6.
17.解:(1)证明:如图,连接OA.
∵DA平分∠BDE, ∴∠ODA=∠EDA.∵OA=OD,∴∠ODA=∠OAD.∴∠OAD=∠EDA.
∴OA∥CE.∵AE是☉O的切线,∴OA⊥AE.∴AE⊥CD.(2)如图,过点O作OF⊥CD,垂足为F.
∵∠OAE=∠AED=∠OFD=90°,∴四边形AOFE是矩形.∴OF=AE=4 cm.∵OF⊥CD,
CD=6 cm,∴DF=12CD=3 cm.在Rt△ODF中,OD=OF2+DF2=5(cm),即☉O的半径为5 cm.
18.解:(1)证明:如图①,连接OC.
在△OAD和△OCD中,AD=CD,OA=OC,OD=OD,∴△OAD≌△OCD(SSS),∴∠ADO=∠CDO.
又AD=CD,∴DE⊥AC.∵AB为☉O的直径,∴∠ACB=90°,即BC⊥AC,∴OD∥BC.
(2)如图②,连接AF,过点F作FM⊥EF交OD于点M.
∵AB=AD,AD是☉O的切线,∴△ABD为等腰直角三角形.∵AB为☉O的直径,
∴∠AFB=90°,∠DAF=45°.∵∠AED=∠AFD=90°,∴∠DAF=∠ADF=45°,∠EAF=∠FDM,
∴AF=DF.∵∠EFM=∠AFD=90°,∴∠AFE=∠DFM,∴△AEF≌△DMF(ASA),
∴AE=DM,EF=MF.∵OA=5,∴AB=AD=25,∴OD=OA2+AD2=5,
∴AE=DM=5×255=2,∴DE=4,∴EM=DE-DM=4-2=2,∴EF=2.
一、选择题(每小题4分,共32分)
1.如图1,AB是☉O的直径,若∠BAC=20°,则∠ADC的度数为 ( )
图1
A.40° B.60° C.70° D.80°
2.若直线l与半径为r的☉O相交,且点O到直线l的距离为6,则r的取值范围是 ( )
A.r<6 B.r=6 C.r>6 D.r≥6
3.如图2,四边形ABCD为☉O的内接四边形,已知∠BCD=120°,则∠BOD的度数为
( )
图2
A.100° B.110° C.120° D.130°
27381202647954.如图3,AB是圆O的弦,OC⊥AB交圆O于点C,D是圆O上一点,∠ADC=35°,则∠BOC的度数为 ( )
A.50° B.60° C.70° D.80° 图3
5.如图4,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,BP=4,则线段AP的长为 ( )
图4
A.4 B.8 C.43 D.42
6.如图5,在?APBC中,∠C=40°.若☉O分别与PA,PB相切于点A,B,则∠CAB的度数为
( )
图5
A.40° B.50° C.60° D.70°
7.如图6,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直,垂足为M.若∠ABC=55°,则∠ACD的度数为( )
图6
A.20° B.35° C.40° D.55°
8.如图7,☉O是△ABC的内切圆,∠ACB=90°,AB=8,∠BOC=105°,则BC的长为( )
图7
A.4 B.3 C.5 D.43
二、填空题(每小题4分,共24分)
9.已知☉O的半径为5,直线AB与☉O相交,则圆心O到直线AB的距离d的取值范围是 .?
10.如图8,AB为☉O的直径,CD是☉O的弦,∠ADC=25°,则∠CAB的度数为 .
图8
11.已知四边形ABCD是☉O的内接四边形,则∠A+∠C= °.?
12.如图9,四边形ABCD内接于☉O,F是CD上一点,且DF=BC,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为 .?
图9
13.如图10,P是☉O外的一点,PA,PB分别和☉O相切于点A,B,C是AB上的任意一点,过点C作☉O的切线分别交PA,PB于点D,E.若△PDE的周长为12,则PA的长为 .?
图10
14.如图11,在平面直角坐标系中,已知C(2,4),以点C为圆心的圆与y轴相切.点A,B在x轴上,且OA=OB.P为☉C上的动点,∠APB=90°,则线段AB长度的最大值为 .?
图11
三、解答题(共44分)
15.(10分)已知:如图12,AB是☉O的直径,直线BC与☉O相切于点B,∠ABC的平分线BD交☉O于点D,AD的延长线交BC于点C.
(1)求证:AD=CD;
(2)求∠BAC的度数.
图12
16.(10分)如图13,△ABC内接于☉O,AB为☉O的直径,直线EF切☉O于点D,且EF∥AB,连接CD,BD.
(1)求证:CD平分∠ACB;
(2)若∠ABC=30°,BD=22,求CD的长.
图13
17.(12分)如图14,四边形ABCD 内接于☉O,BD是☉O的直径,过点A作☉O的切线AE交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE⊥CD;
(2)已知AE=4 cm,CD=6 cm,求☉O的半径.
图14
18.(12分)如图15,在四边形ABCD中,AB=AD=CD,以AB为直径的☉O经过点C,连接AC,OD交于点E.
(1)如图①,求证:OD∥BC;
(2)如图②,若AD是☉O的切线,连接BD交☉O于点F,连接EF,且OA=5,求EF的长.
图15
答案
1.C [解析] ∵AB是☉O的直径,∴∠ACB=90°.∵∠BAC=20°,∴∠ABC=90°-20°=70°,
∴∠ADC=∠ABC=70°.故选C.
2.C
3.C [解析] ∵四边形ABCD是☉O的内接四边形,∴∠A=180°-∠BCD=60°.由圆周角定理,得∠BOD=2∠A=120°.故选C.
4.C [解析] ∵OC⊥AB,∴AC=BC,∴∠AOC=∠BOC.∵∠ADC=35°,∴∠AOC=70°,
∴∠BOC=70°.故选C.
5.C [解析] 连接OA,如图所示.∵PA为☉O的切线,∴PA⊥OA,∴∠OAP=90°.∵∠P=30°,
∴OP=2OA=2OB,AP=3OA,∴OA=OB=BP=4,∴AP=43.故选C.
6.D [解析] ∵☉O分别与PA,PB相切于点A,B,∴PA=PB.∵四边形APBC是平行四边形,
∴四边形APBC是菱形,∴AC=BC.又∵∠C=40°,∴∠CAB=70°.
7.A
8.A [解析] ∵☉O是△ABC的内切圆,∴∠OBC=12∠ABC,∠OCB=12∠ACB.∵∠BOC=105°,
∴∠OBC+∠OCB=180°-105°=75°.∴∠ABC+∠ACB=2×75°=150°.∴∠A=180°-(∠ABC+∠ACB)=30°.∵∠ACB=90°,AB=8,∴BC=12AB=4.故选A.
9.0≤d<5
10.65° [解析] 由圆周角定理,得∠ABC=∠ADC=25°.∵AB为☉O的直径,∴∠ACB=90°.
∴∠CAB=90°-∠ABC=65°.
11.180
12.50° [解析] ∵四边形ABCD内接于☉O,∠ABC=105°,∴∠ADC=180°-∠ABC=180°-105°=
75°.∵DF=BC,∠BAC=25°,∴∠DCE=∠BAC=25°,∴∠E=∠ADC-∠DCE=75°-25°=50°.
13. 6 [解析] 根据切线长定理,得AD=CD,CE=BE,PA=PB,则△PDE的周长=2PA=12,
∴PA=6.
14.45+4 [解析] 连接OC并延长交☉C于点P,此时AB的长度最大.∵C(2,4),
∴OC=22+42=25.∵以点C为圆心的圆与y轴相切,∴☉C的半径为2.∵∠APB=90°,
∴OP=OA=OB=2+25,∴AB长度的最大值为45+4.
15.解:(1)证明:∵AB是☉O的直径,∴∠ADB=90°.∴∠CDB=90°.∴∠ADB=∠CDB.
∵BD平分∠ABC,∴∠ABD=∠CBD.在△ABD和△CBD中,∠ADB=∠CDB,BD=BD,∠ABD=∠CBD,
∴△ABD≌△CBD(ASA).∴AD=CD.
(2)∵△ABD≌△CBD,∴AB=CB.∵直线BC与☉O相切于点B,∴∠ABC=90°.
∴∠BAC=∠C=45°.
16.解:(1)证明:如图,连接OD.∵直线EF切☉O于点D,∴OD⊥EF.∵AB∥EF,
∴OD⊥AB,∴∠AOD=∠BOD=90°,∴AD=BD,∴∠ACD=∠BCD,∴CD平分∠ACB.
(2)由(1)知∠BOD=90°,∴OB=OD=22BD=2,∴AB=2OB=4.∵AB为☉O的直径,∴∠ACB=90°.
又∠ABC=30°,∴AC=12AB=2.如图,连接AD,作AH⊥CD于点H.∵∠ACH=12∠ACB=45°,
∴CH=AH.设CH=x.∵CH2+AH2=AC2,∴x2+x2=22,∴x=2,即AH=CH=2.
∵∠ADC=∠ABC=30°,∴AD=2AH=22,∴DH=6,∴CD=CH+DH=2+6.
17.解:(1)证明:如图,连接OA.
∵DA平分∠BDE, ∴∠ODA=∠EDA.∵OA=OD,∴∠ODA=∠OAD.∴∠OAD=∠EDA.
∴OA∥CE.∵AE是☉O的切线,∴OA⊥AE.∴AE⊥CD.(2)如图,过点O作OF⊥CD,垂足为F.
∵∠OAE=∠AED=∠OFD=90°,∴四边形AOFE是矩形.∴OF=AE=4 cm.∵OF⊥CD,
CD=6 cm,∴DF=12CD=3 cm.在Rt△ODF中,OD=OF2+DF2=5(cm),即☉O的半径为5 cm.
18.解:(1)证明:如图①,连接OC.
在△OAD和△OCD中,AD=CD,OA=OC,OD=OD,∴△OAD≌△OCD(SSS),∴∠ADO=∠CDO.
又AD=CD,∴DE⊥AC.∵AB为☉O的直径,∴∠ACB=90°,即BC⊥AC,∴OD∥BC.
(2)如图②,连接AF,过点F作FM⊥EF交OD于点M.
∵AB=AD,AD是☉O的切线,∴△ABD为等腰直角三角形.∵AB为☉O的直径,
∴∠AFB=90°,∠DAF=45°.∵∠AED=∠AFD=90°,∴∠DAF=∠ADF=45°,∠EAF=∠FDM,
∴AF=DF.∵∠EFM=∠AFD=90°,∴∠AFE=∠DFM,∴△AEF≌△DMF(ASA),
∴AE=DM,EF=MF.∵OA=5,∴AB=AD=25,∴OD=OA2+AD2=5,
∴AE=DM=5×255=2,∴DE=4,∴EM=DE-DM=4-2=2,∴EF=2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
