第6章 一次函数练练习 2021—2022学年苏科版八年级数学上册(word版含解析)
文档属性
| 名称 | 第6章 一次函数练练习 2021—2022学年苏科版八年级数学上册(word版含解析) | 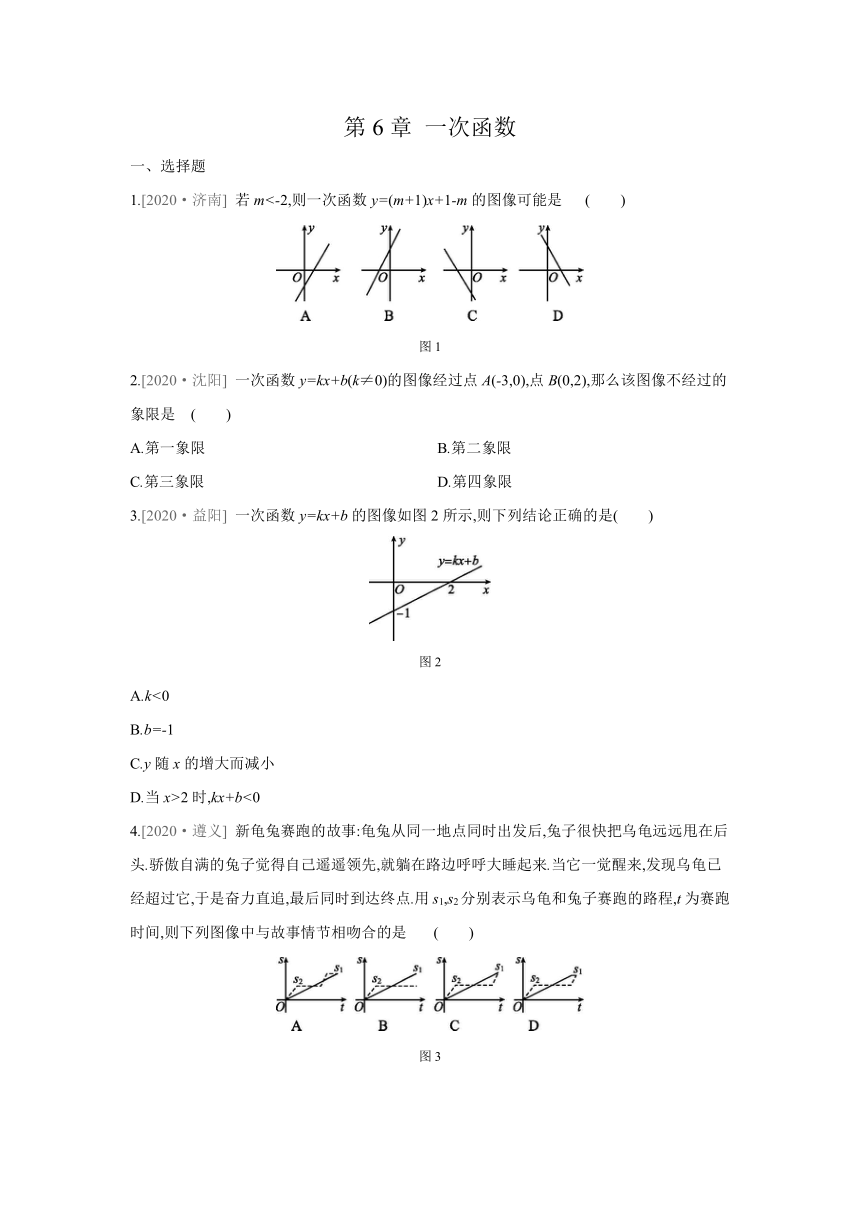 | |
| 格式 | docx | ||
| 文件大小 | 224.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 06:17:30 | ||
图片预览





文档简介
第6章 一次函数
一、选择题
1.[2020·济南] 若m<-2,则一次函数y=(m+1)x+1-m的图像可能是 ( )
图1
2.[2020·沈阳] 一次函数y=kx+b(k≠0)的图像经过点A(-3,0),点B(0,2),那么该图像不经过的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.[2020·益阳] 一次函数y=kx+b的图像如图2所示,则下列结论正确的是( )
图2
A.k<0
B.b=-1
C.y随x的增大而减小
D.当x>2时,kx+b<0
4.[2020·遵义] 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用s1,s2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图像中与故事情节相吻合的是 ( )
图3
5.[2020·湘潭] 如图4,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,x的取值范围为 ( )
图4
A.x≤1 B.x≥1
C.x<1 D.x>1
6.[2020·内江] 在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是 ( )
A.12≤t<2 B.12 C.1二、填空题
7.[2020·宿迁] 已知一次函数y=2x-1的图像经过A(x1,1),B(x2,3)两点,则x1 x2(填“>”“<”或“=”).?
8.[2020·天津] 将直线y=-2x向上平移1个单位长度,平移后直线的表达式为 .?
9.[2020·成都] 一次函数y=(2m-1)x+2的函数值y随x值的增大而增大,则常数m的取值范围为 .?
10.[2020·南京] 将一次函数y=-2x+4的图像绕原点O逆时针旋转90°,所得到的图像对应的函数表达式是 .?
11.[2020·黔西南州] 如图5,正比例函数的图像与一次函数y=-x+1的图像相交于点P,点P到x轴的距离是2,则这个正比例函数的表达式是 .?
图5
12.[2020·黔南州] 如图6,在平面直角坐标系中,直线y=-43x+4与x轴、y轴分别交于A,B两点,点C在第二象限,若BC=OC=OA,则点C的坐标为 .?
图6
13.[2020·达州] 已知k为正整数,无论k取何值,直线l1:y=kx+k+1与直线l2:y=(k+1)x+k+2都交于一个固定的点,这个点的坐标是 ;记直线l1和l2与x轴围成的三角形的面积为Sk,则S1= ,S1+S2+S3+…+S100的值为 .?
三、解答题
14.[2020·滨州] 如图7,在平面直角坐标系中,直线y=-12x-1与直线y=-2x+2相交于点P,并分别与x轴相交于点A,B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图像中直线y=-2x+2在直线y=-12x-1上方的部分描黑加粗,并写出此时自变量x的取值范围.
图7
15.[2020·南通] 如图8,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的表达式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
图8
16.[2020·云南] 众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到A地和B地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:
目的地车型
A地(元/辆)
B地(元/辆)
大货车
900
1000
小货车
500
700
现安排上述装好物资的20辆货车中的10辆前往A地,其余前往B地.设前往A地的大货车有x辆,这20辆货车的总运费为y元.
(1)这20辆货车中,大货车、小货车各有多少辆?
(2)求y关于x的函数表达式,并直接写出x的取值范围;
(3)若运往A地的物资不少于140吨,求总运费y的最小值.
17.[2020·宁夏] “低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y(m)与步行时间x(min)之间的函数关系如图9中折线段AB-BC-CD所示.
(1)小丽与小明出发 min相遇.?
(2)在步行过程中,若小明先到达甲地.
①求小丽和小明步行的速度各是多少;
②计算出点C的坐标,并解释点C的实际意义.
图9
答案
1.D [解析] 因为m<-2,所以m+1<0,1-m>0,所以一次函数y=(m+1)x+1-m的图像经过第一、二、四象限.故选D.
2.D [解析] (方法一)将A(-3,0),B(0,2)代入y=kx+b,得
-3k+b=0,b=2,解得k=23,b=2,
∴一次函数的表达式为y=23x+2.
∵k=23>0,b=2>0,
∴一次函数y=23x+2的图像经过第一、二、三象限,
即该图像不经过第四象限.故选D.
(方法二)依照题意,画出函数图像,如图所示.
观察函数图像,可知一次函数y=kx+b(k≠0)的图像不经过第四象限.故选D.
3.B [解析] 由题图可知,图像经过第一、三、四象限,则k>0,故A选项错误;图像与y轴交于点(0,-1),故b=-1,故B选项正确;k>0,y随x的增大而增大,故C选项错误;当x>2时,kx+b>0,故D选项错误.故选B.
4.C [解析] A项,此函数图像中,s2先达到最大值,即兔子先到终点,不符合题意;
B项,此函数图像中,s2第2段随时间增加其路程一直保持不变,与“当它一觉醒来,发现乌龟已经超过它,于是奋力直追”不符,不符合题意;
C项,此函数图像中,乌龟和兔子同时到达终点,符合题意;
D项,此函数图像中,s1先达到最大值,即乌龟先到终点,不符合题意.故选C.
5.A [解析] 由题意,将P(1,1)代入y=kx+b(k<0),可得k+b=1,即k-1=-b.整理kx+b≥x,得(k-1)x+b≥0,∴-bx+b≥0.由图像可知b>0,∴x-1≤0,∴x≤1.故选A.
6.D [解析] ∵y=tx+2t+2=t(x+2)+2(t>0),
∴直线y=tx+2t+2(t>0)经过点(-2,2).
如图,当直线经过点(0,3)时,直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则3=2t+2,解得t=12;
当直线经过点(0,6)时,直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则6=2t+2,解得t=2;
当直线经过(0,4)时,直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有三个整点,则4=2t+2,解得t=1.
∴直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是12≤t≤2且t≠1.故选D.
7.< [解析] (解法一)∵k=2>0,∴y随x的增大而增大.又∵1<3,∴x1(解法二)当y=1时,2x1-1=1,解得x1=1;当y=3时,2x2-1=3,解得x2=2.又∵1<2,∴x18.y=-2x+1 [解析] 将直线y=-2x向上平移1个单位长度,得到的直线的表达式为y=-2x+1.
9.m>12 [解析] ∵一次函数y=(2m-1)x+2中,函数值y随自变量x的增大而增大,∴2m-1>0,解得m>12.
10.y=12x+2 [解析] 在一次函数y=-2x+4中,令x=0,则y=4,令y=0,则x=2,
∴一次函数y=-2x+4的图像经过点(0,4),(2,0).将一次函数y=-2x+4的图像绕原点O逆时针旋转90°,则点(0,4)的对应点为(-4,0),点(2,0)的对应点是(0,2),
设对应的函数表达式为y=kx+b,
将点(-4,0),(0,2)代入,得-4k+b=0,b=2,
解得k=12,b=2,
∴旋转后所得图像对应的函数表达式为y=12x+2.
11.y=-2x [解析] ∵点P到x轴的距离为2,∴点P的纵坐标为2.∵点P在一次函数y=-x+1的图像上,∴2=-x+1,得x=-1,∴点P的坐标为(-1,2).设正比例函数的表达式为y=kx,则2=-k,得k=-2,∴正比例函数的表达式为y=-2x.
12.(-5,2) [解析] ∵直线y=-43x+4与x轴、y轴分别交于A,B两点,
∴点A的坐标为(3,0),点B的坐标为(0,4).
过点C作CE⊥y轴于点E,如图所示.
∵BC=OC=OA,∴OC=3,OE=2,
∴CE=OC2-OE2=5,
∴点C的坐标为(-5,2).
13.(-1,1) 14 50101 [解析] ∵直线l1:y=kx+k+1=k(x+1)+1,
∴直线l1:y=kx+k+1经过点(-1,1).
∵直线l2:y=(k+1)x+k+2=k(x+1)+(x+1)+1=(k+1)(x+1)+1,
∴直线l2:y=(k+1)x+k+2经过点(-1,1),
∴无论k取何值,直线l1与l2的交点均为定点(-1,1).
∵直线l1:y=kx+k+1与x轴的交点为-k+1k,0,
直线l2:y=(k+1)x+k+2与x轴的交点为-k+2k+1,0,
∴Sk=12×-k+1k+k+2k+1×1=12k(k+1),∴S1=12×11×2=14,
S1+S2+S3+…+S100=1211×2+12×3+…+1100×101
=121-12+12-13+…+1100-1101
=12×1-1101
=12×100101
=50101.
14.解:(1)由y=-12x-1,y=-2x+2,解得x=2,y=-2,
∴P(2,-2).
(2)直线y=-12x-1与直线y=-2x+2中,
令y=0,得-12x-1=0与-2x+2=0,
解得x=-2与x=1,
∴A(-2,0),B(1,0),∴AB=3,
∴S△PAB=12AB·|yP|=12×3×2=3.
(3)如图所示.
自变量x的取值范围是x<2.
15.解:(1)把x=1代入y=x+3,得y=4,
∴C(1,4).
设直线l2的表达式为y=kx+b,
∴k+b=4,3k+b=0,解得k=-2,b=6,
∴直线l2的表达式为y=-2x+6.
(2)在y=x+3中,令y=0,得x=-3,
∴B(-3,0),∴AB=3-(-3)=6.
设M(a,a+3),由MN∥y轴,得N(a,-2a+6),
∴MN=|a+3-(-2a+6)|=AB=6,
解得a=3或a=-1,
∴点M的坐标为(3,6)或(-1,2).
16.解:(1)设大货车、小货车分别有a辆、b辆,由题意,得
15a+10b=260,a+b=20,
解得a=12,b=8.
答:大货车、小货车分别有12辆、8辆.
(2)由到A地的大货车有x辆,
则到A地的小货车有(10-x)辆,
到B地的大货车有(12-x)辆,
到B地的小货车有(x-2)辆,
∴y=900x+500(10-x)+1000(12-x)+700(x-2)=100x+15600,
其中2≤x≤10,且x是正整数.
(3)运往A地的物资共有[15x+10(10-x)]吨.
由题意,得15x+10(10-x)≥140,
解得x≥8,
∴8≤x≤10.
由总运费y=100x+15600(8≤x≤10).
∵k=100>0,∴y随x的增大而增大,
∴当x=8时,y有最小值,此时y=100×8+15600=16400(元).
答:总运费y的最小值为16400元.
17.解:(1)30
(2)①设小丽步行的速度为V1 m/min,小明步行的速度为V2 m/min,且V2>V1,
则30V1+30V2=5400,(67.5-30)V1=30V2,
解得V1=80,V2=100.
答:小丽步行的速度为80 m/min,小明步行的速度为100 m/min.
②5400÷100=54(min),54×80=4320(m),
∴点C(54,4320).
点C的实际意义:两人出发54 min时,小明到达甲地,此时两人相距4320 m.
一、选择题
1.[2020·济南] 若m<-2,则一次函数y=(m+1)x+1-m的图像可能是 ( )
图1
2.[2020·沈阳] 一次函数y=kx+b(k≠0)的图像经过点A(-3,0),点B(0,2),那么该图像不经过的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.[2020·益阳] 一次函数y=kx+b的图像如图2所示,则下列结论正确的是( )
图2
A.k<0
B.b=-1
C.y随x的增大而减小
D.当x>2时,kx+b<0
4.[2020·遵义] 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用s1,s2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图像中与故事情节相吻合的是 ( )
图3
5.[2020·湘潭] 如图4,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,x的取值范围为 ( )
图4
A.x≤1 B.x≥1
C.x<1 D.x>1
6.[2020·内江] 在平面直角坐标系中,横坐标和纵坐标都是整数的点叫做整点,已知直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是 ( )
A.12≤t<2 B.12
7.[2020·宿迁] 已知一次函数y=2x-1的图像经过A(x1,1),B(x2,3)两点,则x1 x2(填“>”“<”或“=”).?
8.[2020·天津] 将直线y=-2x向上平移1个单位长度,平移后直线的表达式为 .?
9.[2020·成都] 一次函数y=(2m-1)x+2的函数值y随x值的增大而增大,则常数m的取值范围为 .?
10.[2020·南京] 将一次函数y=-2x+4的图像绕原点O逆时针旋转90°,所得到的图像对应的函数表达式是 .?
11.[2020·黔西南州] 如图5,正比例函数的图像与一次函数y=-x+1的图像相交于点P,点P到x轴的距离是2,则这个正比例函数的表达式是 .?
图5
12.[2020·黔南州] 如图6,在平面直角坐标系中,直线y=-43x+4与x轴、y轴分别交于A,B两点,点C在第二象限,若BC=OC=OA,则点C的坐标为 .?
图6
13.[2020·达州] 已知k为正整数,无论k取何值,直线l1:y=kx+k+1与直线l2:y=(k+1)x+k+2都交于一个固定的点,这个点的坐标是 ;记直线l1和l2与x轴围成的三角形的面积为Sk,则S1= ,S1+S2+S3+…+S100的值为 .?
三、解答题
14.[2020·滨州] 如图7,在平面直角坐标系中,直线y=-12x-1与直线y=-2x+2相交于点P,并分别与x轴相交于点A,B.
(1)求交点P的坐标;
(2)求△PAB的面积;
(3)请把图像中直线y=-2x+2在直线y=-12x-1上方的部分描黑加粗,并写出此时自变量x的取值范围.
图7
15.[2020·南通] 如图8,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的表达式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
图8
16.[2020·云南] 众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到A地和B地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:
目的地车型
A地(元/辆)
B地(元/辆)
大货车
900
1000
小货车
500
700
现安排上述装好物资的20辆货车中的10辆前往A地,其余前往B地.设前往A地的大货车有x辆,这20辆货车的总运费为y元.
(1)这20辆货车中,大货车、小货车各有多少辆?
(2)求y关于x的函数表达式,并直接写出x的取值范围;
(3)若运往A地的物资不少于140吨,求总运费y的最小值.
17.[2020·宁夏] “低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y(m)与步行时间x(min)之间的函数关系如图9中折线段AB-BC-CD所示.
(1)小丽与小明出发 min相遇.?
(2)在步行过程中,若小明先到达甲地.
①求小丽和小明步行的速度各是多少;
②计算出点C的坐标,并解释点C的实际意义.
图9
答案
1.D [解析] 因为m<-2,所以m+1<0,1-m>0,所以一次函数y=(m+1)x+1-m的图像经过第一、二、四象限.故选D.
2.D [解析] (方法一)将A(-3,0),B(0,2)代入y=kx+b,得
-3k+b=0,b=2,解得k=23,b=2,
∴一次函数的表达式为y=23x+2.
∵k=23>0,b=2>0,
∴一次函数y=23x+2的图像经过第一、二、三象限,
即该图像不经过第四象限.故选D.
(方法二)依照题意,画出函数图像,如图所示.
观察函数图像,可知一次函数y=kx+b(k≠0)的图像不经过第四象限.故选D.
3.B [解析] 由题图可知,图像经过第一、三、四象限,则k>0,故A选项错误;图像与y轴交于点(0,-1),故b=-1,故B选项正确;k>0,y随x的增大而增大,故C选项错误;当x>2时,kx+b>0,故D选项错误.故选B.
4.C [解析] A项,此函数图像中,s2先达到最大值,即兔子先到终点,不符合题意;
B项,此函数图像中,s2第2段随时间增加其路程一直保持不变,与“当它一觉醒来,发现乌龟已经超过它,于是奋力直追”不符,不符合题意;
C项,此函数图像中,乌龟和兔子同时到达终点,符合题意;
D项,此函数图像中,s1先达到最大值,即乌龟先到终点,不符合题意.故选C.
5.A [解析] 由题意,将P(1,1)代入y=kx+b(k<0),可得k+b=1,即k-1=-b.整理kx+b≥x,得(k-1)x+b≥0,∴-bx+b≥0.由图像可知b>0,∴x-1≤0,∴x≤1.故选A.
6.D [解析] ∵y=tx+2t+2=t(x+2)+2(t>0),
∴直线y=tx+2t+2(t>0)经过点(-2,2).
如图,当直线经过点(0,3)时,直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则3=2t+2,解得t=12;
当直线经过点(0,6)时,直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则6=2t+2,解得t=2;
当直线经过(0,4)时,直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有三个整点,则4=2t+2,解得t=1.
∴直线y=tx+2t+2(t>0)与两坐标轴围成的三角形区域(不含边界)中有且只有四个整点,则t的取值范围是12≤t≤2且t≠1.故选D.
7.< [解析] (解法一)∵k=2>0,∴y随x的增大而增大.又∵1<3,∴x1
9.m>12 [解析] ∵一次函数y=(2m-1)x+2中,函数值y随自变量x的增大而增大,∴2m-1>0,解得m>12.
10.y=12x+2 [解析] 在一次函数y=-2x+4中,令x=0,则y=4,令y=0,则x=2,
∴一次函数y=-2x+4的图像经过点(0,4),(2,0).将一次函数y=-2x+4的图像绕原点O逆时针旋转90°,则点(0,4)的对应点为(-4,0),点(2,0)的对应点是(0,2),
设对应的函数表达式为y=kx+b,
将点(-4,0),(0,2)代入,得-4k+b=0,b=2,
解得k=12,b=2,
∴旋转后所得图像对应的函数表达式为y=12x+2.
11.y=-2x [解析] ∵点P到x轴的距离为2,∴点P的纵坐标为2.∵点P在一次函数y=-x+1的图像上,∴2=-x+1,得x=-1,∴点P的坐标为(-1,2).设正比例函数的表达式为y=kx,则2=-k,得k=-2,∴正比例函数的表达式为y=-2x.
12.(-5,2) [解析] ∵直线y=-43x+4与x轴、y轴分别交于A,B两点,
∴点A的坐标为(3,0),点B的坐标为(0,4).
过点C作CE⊥y轴于点E,如图所示.
∵BC=OC=OA,∴OC=3,OE=2,
∴CE=OC2-OE2=5,
∴点C的坐标为(-5,2).
13.(-1,1) 14 50101 [解析] ∵直线l1:y=kx+k+1=k(x+1)+1,
∴直线l1:y=kx+k+1经过点(-1,1).
∵直线l2:y=(k+1)x+k+2=k(x+1)+(x+1)+1=(k+1)(x+1)+1,
∴直线l2:y=(k+1)x+k+2经过点(-1,1),
∴无论k取何值,直线l1与l2的交点均为定点(-1,1).
∵直线l1:y=kx+k+1与x轴的交点为-k+1k,0,
直线l2:y=(k+1)x+k+2与x轴的交点为-k+2k+1,0,
∴Sk=12×-k+1k+k+2k+1×1=12k(k+1),∴S1=12×11×2=14,
S1+S2+S3+…+S100=1211×2+12×3+…+1100×101
=121-12+12-13+…+1100-1101
=12×1-1101
=12×100101
=50101.
14.解:(1)由y=-12x-1,y=-2x+2,解得x=2,y=-2,
∴P(2,-2).
(2)直线y=-12x-1与直线y=-2x+2中,
令y=0,得-12x-1=0与-2x+2=0,
解得x=-2与x=1,
∴A(-2,0),B(1,0),∴AB=3,
∴S△PAB=12AB·|yP|=12×3×2=3.
(3)如图所示.
自变量x的取值范围是x<2.
15.解:(1)把x=1代入y=x+3,得y=4,
∴C(1,4).
设直线l2的表达式为y=kx+b,
∴k+b=4,3k+b=0,解得k=-2,b=6,
∴直线l2的表达式为y=-2x+6.
(2)在y=x+3中,令y=0,得x=-3,
∴B(-3,0),∴AB=3-(-3)=6.
设M(a,a+3),由MN∥y轴,得N(a,-2a+6),
∴MN=|a+3-(-2a+6)|=AB=6,
解得a=3或a=-1,
∴点M的坐标为(3,6)或(-1,2).
16.解:(1)设大货车、小货车分别有a辆、b辆,由题意,得
15a+10b=260,a+b=20,
解得a=12,b=8.
答:大货车、小货车分别有12辆、8辆.
(2)由到A地的大货车有x辆,
则到A地的小货车有(10-x)辆,
到B地的大货车有(12-x)辆,
到B地的小货车有(x-2)辆,
∴y=900x+500(10-x)+1000(12-x)+700(x-2)=100x+15600,
其中2≤x≤10,且x是正整数.
(3)运往A地的物资共有[15x+10(10-x)]吨.
由题意,得15x+10(10-x)≥140,
解得x≥8,
∴8≤x≤10.
由总运费y=100x+15600(8≤x≤10).
∵k=100>0,∴y随x的增大而增大,
∴当x=8时,y有最小值,此时y=100×8+15600=16400(元).
答:总运费y的最小值为16400元.
17.解:(1)30
(2)①设小丽步行的速度为V1 m/min,小明步行的速度为V2 m/min,且V2>V1,
则30V1+30V2=5400,(67.5-30)V1=30V2,
解得V1=80,V2=100.
答:小丽步行的速度为80 m/min,小明步行的速度为100 m/min.
②5400÷100=54(min),54×80=4320(m),
∴点C(54,4320).
点C的实际意义:两人出发54 min时,小明到达甲地,此时两人相距4320 m.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
