《逻辑的力量》课件22张PPT 2021-2022学年统编版高中语文选择性必修上册第四单元
文档属性
| 名称 | 《逻辑的力量》课件22张PPT 2021-2022学年统编版高中语文选择性必修上册第四单元 |  | |
| 格式 | pptx | ||
| 文件大小 | 331.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 统编版 | ||
| 科目 | 语文 | ||
| 更新时间 | 2021-07-20 07:34:54 | ||
图片预览







文档简介
逻辑谬误与推理
——逻辑的力量
烛之武入情入理的分析挽救了国家,这是外交中的逻辑;
林庚细致辨析“木叶”的内涵,这是文艺鉴赏中的逻辑;
王安石驳斥对变法的非难,这是治国理政中的逻辑。
逻辑是什么?《现代汉语词典》释义为思维的规律。狭义的思维是指理性认识,恩格斯在《自然辩证法》中写到“地球上最美的花朵是思维着的精神”,思维有多远,人类就能走多远。
下面,就让我们开启一段发现谬误,探寻推理的“逻辑之旅”,一起走到天尽头。
导入:
学习目标:
1、探究逻辑的基本规律,梳理总结常见的逻辑谬误类型,学会识别反击谬误
2、从具体的语言材料中,概括出推理过程,初步认识常见的推理形式
充分理由律
排中律
同一律
(不)矛盾律
逻辑规律
一:发现潜藏的逻辑谬误
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}逻辑规律
公式
要求
(同一时间同一方面对
同一对象)
逻辑错误
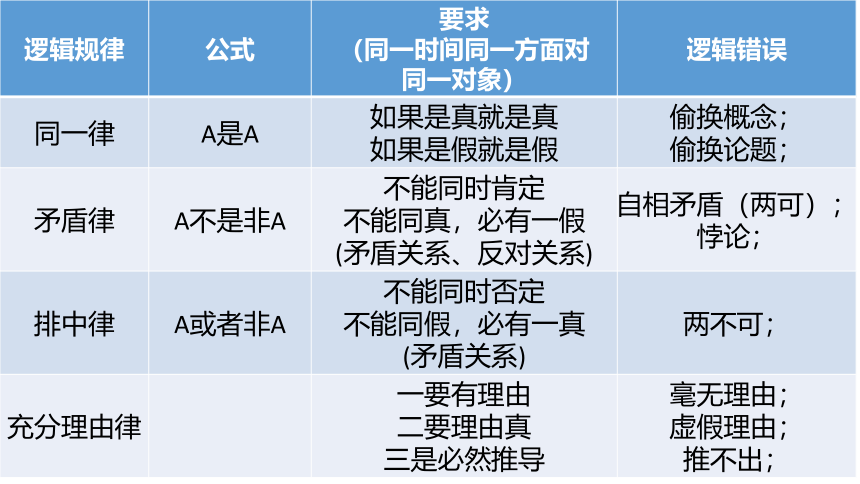
同一律
A是A
如果是真就是真
如果是假就是假
偷换概念;
偷换论题;
矛盾律
A不是非A
不能同时肯定
不能同真,必有一假
(矛盾关系、反对关系)
自相矛盾(两可);
悖论;
排中律
A或者非A
不能同时否定
不能同假,必有一真
(矛盾关系)
两不可;
充分理由律
一要有理由
二要理由真
三是必然推导
毫无理由;
虚假理由;
推不出;
1919年,英国著名的数学家、逻辑学家罗素曾经提出一个问题“某村子里有个理发师,他规定:在本村我只给而且一定要给那些自己不刮胡子的人刮胡子。”这是数学史上著名的“理发师悖论”,可是随着时间的推移,理发师胡子越长越长。
请问:这个理发师能不能给自己刮胡子?请分析其包含的逻辑矛盾。
现场加试:
不刮——属于“不给自己刮脸的人”,
他就要给自己刮脸,
刮 ——又属于“给自己刮脸的人”,
他就不能给自己刮脸。
悖论——违反矛盾律
莎士比亚的《威尼斯商人》中:富家少女鲍西娅姿容绝世德性完美。许多王孙公子来求婚。鲍西娅的父亲在遗嘱中规定要“猜匣为婚”,否则要取消她的遗产继承权。鲍西娅家有三只匣子:金匣子、银匣子和铅匣子。但只有一个匣子里放着鲍西娅的肖像。匣子上分别刻着一句话:
金匣子上刻的是“肖像不在此匣中”;
银匣子上刻的是“肖像在金匣中”;
铅匣子上刻的是“肖像不在此匣中”。
旁边的一张大纸上写着:“这三句话中只有一句是真话。”
鲍西娅父亲的遗言是:猜中鲍西娅的肖像放在哪个匣子,鲍西娅就嫁给谁。
金匣子里的话和银匣子里的话是矛盾关系,请根据 律
先断定这其中必有一真话,
再根据“这三句话中只有一句是真话”的提示,
可以推断出铅匣子的话是假话,
既然铅匣子的“肖像不在此匣中”是假话,
肖像就在铅匣子里的结论。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}逻辑规律
公式
要求
(同一时间同一方面对
同一对象)
逻辑错误
同一律
A是A
如果是真就是真
如果是假就是假
偷换概念;
偷换论题;
矛盾律
A不是非A
不能同时肯定
不能同真,必有一假
(矛盾关系、反对关系)
自相矛盾(两可);
悖论;
排中律
A或者非A
不能同时否定
不能同假,必有一真
(矛盾关系)
两不可;
充分理由律
一要有理由
二要理由真
三是必然推导
毫无理由;
虚假理由;
推不出;
在真理面前,一千个权威抵不上一个谦恭的逻辑推理。
——伽利略
类比推理
归纳推理
演绎推理
(一种推理方法,由一般原理推出关于特殊情况下的结论)
三段论
必要条件推理
排除法
充分条件推理
二难推理
二:运用有效地推理形式
从一个或几个已有的判断推出一个新判断的思维形式叫作推理。
推理所依据的已有的判断叫作推理的前提,推出的新判断叫作推理的结论。
注:非完全逻辑学专业术语,常见的几种推理方法
推理
(依据个别与一般的关系)
三段论推理是由一个共同概念把两个判断连接起来,得出一个新的判断作为结论的推理。整个推理由三个简单判断组成,所以称“三段论”。例如:
所有的虚词都是词
所有的介词都是虚词
所有的介词都是词
推理形式:
所有M都是P
所有S都是M
所有S都是P
注:习惯上一般用M表示中项,用P表示大项,用S表示小项
虚词 词 介词
演绎推理之三段论
M
S
P
一般前提和结论之间用横线隔开
但并不是所有符合三段论定义的推理形式都是有效的,《十五贯》中过于执的推理就是一个无效的三段论。过于执得推理过程为:
杀死尤葫芦的罪犯有十五贯钱
熊友兰有十五贯钱
熊友兰是杀死尤葫芦的罪犯
其推理形式概括为:
所有M都是P
所有S都是P
所有S都是M
M
S
P
P
P
S
S
M
M
83页哪个小题也是无效三段论
所谓“充分条件”,就是有这个条件,就一定有相应的结论。通常用“如果p,那么q”的形式表示p是q的充分条件。一般称p为前件,称q为后件。
其所断定的前件和后件的关系是:前件真,后件就一定真。反过来看,后件假,前件就一定假。
依据这种逻辑性质进行充分条件推理时,
如果肯定了前件,结论就可以肯定后件;
如果否定了后件,结论就可以否定前件。
用直角三角形和三角形描述充分条件推理,怎么概括?
如果一个角是直角三角形p,那么它就是三角形q
是直角三角形p
所以就是三角形q
如果一个角是直角三角形p,那么它就是三角形q
不是三角形q
所以就不会是直角三角形p
演绎推理之充分条件推理
第一种有效形式:
肯定前件
如果p,那么q
P
q
第二种有效形式:
否定后件
如果p,那么q
并非q
并非p
袁滋的推理过程概括为:
如果县官以土换金P,那么是金子应该很重很多人抬q
事实上运“金”的只有两个人,用竹扁担(不重且两人)。非q
所以县官不可能以土换金。非P
通常用“只有p,才q”的形式表现必要条件关系,p是q的必要条件,没有p就没有q。其所断定的前件和后件的关系是:前件假,后件就一定假。反过来看,后件真,前件就一定真。
依据这种逻辑性质进行必要条件推理时,
如果否定了前件,结论就可以否定后件;
如果肯定了后件,结论就可以肯定前件。
用三角形和直角三角形描述必要条件推理,怎样概括?
只有是三角形p,才能是直角三角形q
不是三角形p
所以一定不是直角三角形q
只有是三角形p,才能是直角三角形q
是直角三角形q
一定是三角形p
例如:①《晏子使楚》
演绎推理之必要条件推理
第一种有效式:
只有p,才q
并非p,
非q
第二种有效形式:
只有p,才q
q
p
演绎推理之排除法P84②推理过程如下:
如果确定石兽还在河中,要么在原地,要么在下游,要么在上游。
原地和下游都没有,
那就只能在上游了。
推理形式可以这样概括:
一件事共有n种可能存在,排除了(n-1) 种可能,剩下最后一种成为必然。
演绎推理之二难推理P84③人们常运用这种推理逼使对方在两种情况下作出选择,不管选择哪种,都令对方陷入进退维谷。
推理过程如下: 推理形式
如果我去劝解,黛玉会烦恼郁结于心而致疾 如果p,那么r
如果我不去功解,黛玉会过于伤感而致疾 如果q,那么r
或者我去劝解,或者我不去劝解 p或者q
总之黛玉会致疾 总之r
人们认识事物,总是先通过观察、实验和社会调查等途径搜集有关对象的事实材料,对它们进行整理和加工,得到一 些个别性或特殊性知识。然后以这些个别性或特殊性知识为前提,推出一般性的结论。这种推理形式叫作归纳推理。其前提小,结论大,前提真,结论不一定真,是或然推理。
归纳推理
推理形式:
S1是P
S2是P
Sn是P
所有S是P
推理过程概括如下:
白菜因稀缺而珍贵
芦荟因稀缺而珍贵
事物因稀缺而珍贵
三段论推理过程:
事物因稀缺而珍贵
白菜(芦荟)是事物
白菜(芦荟)因稀缺而珍贵
推理形式:
S是P
S1是S
S1是P
《邹忌讽齐王纳谏》结论是“王之蔽甚矣”,它是如何推出的呢?从邹忌自己受到蒙蔽推出的。但是,为什么邹总受蒙敲,王也会受蒙蔽呢?邹忌自己受蒙蔽,是因为那些进言的人和他存在“私”“畏”“有求”的关系,而向王进言的人和王也有类似关系。
推理过程:
A我身边的人和我有情感利害关系c,
他们没有告诉我关于我和徐公就美的真相d
B大王身边的乃至普天下的人和大王都有情感或利害关系c
他们也不会告诉大王一些事情的真相d
推理形式:
A对象具有c、d属性
B对象也具有c属性
B对象也具有d属性
人们认识事物,常常会用已经认识的某个或某类事物去推断尚未认识的另一个或另一类事物。这就需要运用类比推理。类比推理就是根据两个或两类对象在一些属性上相同或相似,推出它们在其他属性上也相同或相似的推理。
类比是一个伟大的引路人。
——波利亚
蛙眼——跟踪卫星
蝙蝠——雷达
……仿生学
类比推理
19年高考全国Ⅰ卷第4题考查断臂维纳斯的身高,如果不运算,使用推理方法定答案,请说出你的答案和推理过程。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}推理分类
前提与结论
前提与结论
前提与结论
是否有必然联系
演绎推理
一般性前提
推出
个别性结论
前提范围大
结论范围小
必然推理
归纳推理
个别性前提
推出
一般性结论
前提范围小
结论范围大
或然推理
(除完全归纳推理外)
类比推理
一般性前提推出一般性结论
个别性前提推出个别性结论
前提结论范围
大小同
或然推理
烛之武入情入理的分析挽救了国家,这是外交中的逻辑;
如果p,那么q
并非q
并非p
林庚细致辨析“木叶”的内涵,这是文艺鉴赏中的逻辑;
S1是P
S2是P
Sn是P
所有S是P
王安石驳斥对变法的非难,这是治国理政中的逻辑。
所有M都是P
所有S都是M
所有S都是P
小
结
若亡郑而有益于君
邻之厚,君之薄也
不要亡郑
名实已明,而天下之理得矣
安石变法名实已明(第二段)
安石变法之理得矣
袅袅兮秋风,洞庭波兮木叶下——疏朗
木叶下,江波连,秋月照浦云歇山——疏朗
亭皋木叶下,陇首秋云飞——疏朗
九月寒砧催木叶,十年征戍忆辽阳——疏朗
木叶营造的意境是疏朗的
学习逻辑,
研究思维的规律,
增强思维能力,
滋养理性精神,
提高思维品质。
希望在今后的学习生活中,
分析如烛之武入情入理,
辨析如林庚的细致条理,
驳斥如王安石大气得理。
三、作业:
1、做2020全国卷Ⅲ论述类文本,辨析逻辑错误
2、预习专题三采用合理的论证方法
——逻辑的力量
烛之武入情入理的分析挽救了国家,这是外交中的逻辑;
林庚细致辨析“木叶”的内涵,这是文艺鉴赏中的逻辑;
王安石驳斥对变法的非难,这是治国理政中的逻辑。
逻辑是什么?《现代汉语词典》释义为思维的规律。狭义的思维是指理性认识,恩格斯在《自然辩证法》中写到“地球上最美的花朵是思维着的精神”,思维有多远,人类就能走多远。
下面,就让我们开启一段发现谬误,探寻推理的“逻辑之旅”,一起走到天尽头。
导入:
学习目标:
1、探究逻辑的基本规律,梳理总结常见的逻辑谬误类型,学会识别反击谬误
2、从具体的语言材料中,概括出推理过程,初步认识常见的推理形式
充分理由律
排中律
同一律
(不)矛盾律
逻辑规律
一:发现潜藏的逻辑谬误
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}逻辑规律
公式
要求
(同一时间同一方面对
同一对象)
逻辑错误
同一律
A是A
如果是真就是真
如果是假就是假
偷换概念;
偷换论题;
矛盾律
A不是非A
不能同时肯定
不能同真,必有一假
(矛盾关系、反对关系)
自相矛盾(两可);
悖论;
排中律
A或者非A
不能同时否定
不能同假,必有一真
(矛盾关系)
两不可;
充分理由律
一要有理由
二要理由真
三是必然推导
毫无理由;
虚假理由;
推不出;
1919年,英国著名的数学家、逻辑学家罗素曾经提出一个问题“某村子里有个理发师,他规定:在本村我只给而且一定要给那些自己不刮胡子的人刮胡子。”这是数学史上著名的“理发师悖论”,可是随着时间的推移,理发师胡子越长越长。
请问:这个理发师能不能给自己刮胡子?请分析其包含的逻辑矛盾。
现场加试:
不刮——属于“不给自己刮脸的人”,
他就要给自己刮脸,
刮 ——又属于“给自己刮脸的人”,
他就不能给自己刮脸。
悖论——违反矛盾律
莎士比亚的《威尼斯商人》中:富家少女鲍西娅姿容绝世德性完美。许多王孙公子来求婚。鲍西娅的父亲在遗嘱中规定要“猜匣为婚”,否则要取消她的遗产继承权。鲍西娅家有三只匣子:金匣子、银匣子和铅匣子。但只有一个匣子里放着鲍西娅的肖像。匣子上分别刻着一句话:
金匣子上刻的是“肖像不在此匣中”;
银匣子上刻的是“肖像在金匣中”;
铅匣子上刻的是“肖像不在此匣中”。
旁边的一张大纸上写着:“这三句话中只有一句是真话。”
鲍西娅父亲的遗言是:猜中鲍西娅的肖像放在哪个匣子,鲍西娅就嫁给谁。
金匣子里的话和银匣子里的话是矛盾关系,请根据 律
先断定这其中必有一真话,
再根据“这三句话中只有一句是真话”的提示,
可以推断出铅匣子的话是假话,
既然铅匣子的“肖像不在此匣中”是假话,
肖像就在铅匣子里的结论。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}逻辑规律
公式
要求
(同一时间同一方面对
同一对象)
逻辑错误
同一律
A是A
如果是真就是真
如果是假就是假
偷换概念;
偷换论题;
矛盾律
A不是非A
不能同时肯定
不能同真,必有一假
(矛盾关系、反对关系)
自相矛盾(两可);
悖论;
排中律
A或者非A
不能同时否定
不能同假,必有一真
(矛盾关系)
两不可;
充分理由律
一要有理由
二要理由真
三是必然推导
毫无理由;
虚假理由;
推不出;
在真理面前,一千个权威抵不上一个谦恭的逻辑推理。
——伽利略
类比推理
归纳推理
演绎推理
(一种推理方法,由一般原理推出关于特殊情况下的结论)
三段论
必要条件推理
排除法
充分条件推理
二难推理
二:运用有效地推理形式
从一个或几个已有的判断推出一个新判断的思维形式叫作推理。
推理所依据的已有的判断叫作推理的前提,推出的新判断叫作推理的结论。
注:非完全逻辑学专业术语,常见的几种推理方法
推理
(依据个别与一般的关系)
三段论推理是由一个共同概念把两个判断连接起来,得出一个新的判断作为结论的推理。整个推理由三个简单判断组成,所以称“三段论”。例如:
所有的虚词都是词
所有的介词都是虚词
所有的介词都是词
推理形式:
所有M都是P
所有S都是M
所有S都是P
注:习惯上一般用M表示中项,用P表示大项,用S表示小项
虚词 词 介词
演绎推理之三段论
M
S
P
一般前提和结论之间用横线隔开
但并不是所有符合三段论定义的推理形式都是有效的,《十五贯》中过于执的推理就是一个无效的三段论。过于执得推理过程为:
杀死尤葫芦的罪犯有十五贯钱
熊友兰有十五贯钱
熊友兰是杀死尤葫芦的罪犯
其推理形式概括为:
所有M都是P
所有S都是P
所有S都是M
M
S
P
P
P
S
S
M
M
83页哪个小题也是无效三段论
所谓“充分条件”,就是有这个条件,就一定有相应的结论。通常用“如果p,那么q”的形式表示p是q的充分条件。一般称p为前件,称q为后件。
其所断定的前件和后件的关系是:前件真,后件就一定真。反过来看,后件假,前件就一定假。
依据这种逻辑性质进行充分条件推理时,
如果肯定了前件,结论就可以肯定后件;
如果否定了后件,结论就可以否定前件。
用直角三角形和三角形描述充分条件推理,怎么概括?
如果一个角是直角三角形p,那么它就是三角形q
是直角三角形p
所以就是三角形q
如果一个角是直角三角形p,那么它就是三角形q
不是三角形q
所以就不会是直角三角形p
演绎推理之充分条件推理
第一种有效形式:
肯定前件
如果p,那么q
P
q
第二种有效形式:
否定后件
如果p,那么q
并非q
并非p
袁滋的推理过程概括为:
如果县官以土换金P,那么是金子应该很重很多人抬q
事实上运“金”的只有两个人,用竹扁担(不重且两人)。非q
所以县官不可能以土换金。非P
通常用“只有p,才q”的形式表现必要条件关系,p是q的必要条件,没有p就没有q。其所断定的前件和后件的关系是:前件假,后件就一定假。反过来看,后件真,前件就一定真。
依据这种逻辑性质进行必要条件推理时,
如果否定了前件,结论就可以否定后件;
如果肯定了后件,结论就可以肯定前件。
用三角形和直角三角形描述必要条件推理,怎样概括?
只有是三角形p,才能是直角三角形q
不是三角形p
所以一定不是直角三角形q
只有是三角形p,才能是直角三角形q
是直角三角形q
一定是三角形p
例如:①《晏子使楚》
演绎推理之必要条件推理
第一种有效式:
只有p,才q
并非p,
非q
第二种有效形式:
只有p,才q
q
p
演绎推理之排除法P84②推理过程如下:
如果确定石兽还在河中,要么在原地,要么在下游,要么在上游。
原地和下游都没有,
那就只能在上游了。
推理形式可以这样概括:
一件事共有n种可能存在,排除了(n-1) 种可能,剩下最后一种成为必然。
演绎推理之二难推理P84③人们常运用这种推理逼使对方在两种情况下作出选择,不管选择哪种,都令对方陷入进退维谷。
推理过程如下: 推理形式
如果我去劝解,黛玉会烦恼郁结于心而致疾 如果p,那么r
如果我不去功解,黛玉会过于伤感而致疾 如果q,那么r
或者我去劝解,或者我不去劝解 p或者q
总之黛玉会致疾 总之r
人们认识事物,总是先通过观察、实验和社会调查等途径搜集有关对象的事实材料,对它们进行整理和加工,得到一 些个别性或特殊性知识。然后以这些个别性或特殊性知识为前提,推出一般性的结论。这种推理形式叫作归纳推理。其前提小,结论大,前提真,结论不一定真,是或然推理。
归纳推理
推理形式:
S1是P
S2是P
Sn是P
所有S是P
推理过程概括如下:
白菜因稀缺而珍贵
芦荟因稀缺而珍贵
事物因稀缺而珍贵
三段论推理过程:
事物因稀缺而珍贵
白菜(芦荟)是事物
白菜(芦荟)因稀缺而珍贵
推理形式:
S是P
S1是S
S1是P
《邹忌讽齐王纳谏》结论是“王之蔽甚矣”,它是如何推出的呢?从邹忌自己受到蒙蔽推出的。但是,为什么邹总受蒙敲,王也会受蒙蔽呢?邹忌自己受蒙蔽,是因为那些进言的人和他存在“私”“畏”“有求”的关系,而向王进言的人和王也有类似关系。
推理过程:
A我身边的人和我有情感利害关系c,
他们没有告诉我关于我和徐公就美的真相d
B大王身边的乃至普天下的人和大王都有情感或利害关系c
他们也不会告诉大王一些事情的真相d
推理形式:
A对象具有c、d属性
B对象也具有c属性
B对象也具有d属性
人们认识事物,常常会用已经认识的某个或某类事物去推断尚未认识的另一个或另一类事物。这就需要运用类比推理。类比推理就是根据两个或两类对象在一些属性上相同或相似,推出它们在其他属性上也相同或相似的推理。
类比是一个伟大的引路人。
——波利亚
蛙眼——跟踪卫星
蝙蝠——雷达
……仿生学
类比推理
19年高考全国Ⅰ卷第4题考查断臂维纳斯的身高,如果不运算,使用推理方法定答案,请说出你的答案和推理过程。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}推理分类
前提与结论
前提与结论
前提与结论
是否有必然联系
演绎推理
一般性前提
推出
个别性结论
前提范围大
结论范围小
必然推理
归纳推理
个别性前提
推出
一般性结论
前提范围小
结论范围大
或然推理
(除完全归纳推理外)
类比推理
一般性前提推出一般性结论
个别性前提推出个别性结论
前提结论范围
大小同
或然推理
烛之武入情入理的分析挽救了国家,这是外交中的逻辑;
如果p,那么q
并非q
并非p
林庚细致辨析“木叶”的内涵,这是文艺鉴赏中的逻辑;
S1是P
S2是P
Sn是P
所有S是P
王安石驳斥对变法的非难,这是治国理政中的逻辑。
所有M都是P
所有S都是M
所有S都是P
小
结
若亡郑而有益于君
邻之厚,君之薄也
不要亡郑
名实已明,而天下之理得矣
安石变法名实已明(第二段)
安石变法之理得矣
袅袅兮秋风,洞庭波兮木叶下——疏朗
木叶下,江波连,秋月照浦云歇山——疏朗
亭皋木叶下,陇首秋云飞——疏朗
九月寒砧催木叶,十年征戍忆辽阳——疏朗
木叶营造的意境是疏朗的
学习逻辑,
研究思维的规律,
增强思维能力,
滋养理性精神,
提高思维品质。
希望在今后的学习生活中,
分析如烛之武入情入理,
辨析如林庚的细致条理,
驳斥如王安石大气得理。
三、作业:
1、做2020全国卷Ⅲ论述类文本,辨析逻辑错误
2、预习专题三采用合理的论证方法
