2.5.1直线与圆的位置关系-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册 25张PPT
文档属性
| 名称 | 2.5.1直线与圆的位置关系-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册 25张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 667.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览






文档简介
2.5.1 直线与圆的位置关系
3、平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
复习
2、圆的一般方程:
1、圆心C(a,b),半径r的圆的标准方程为(x-a)2+(y-b)2=r2
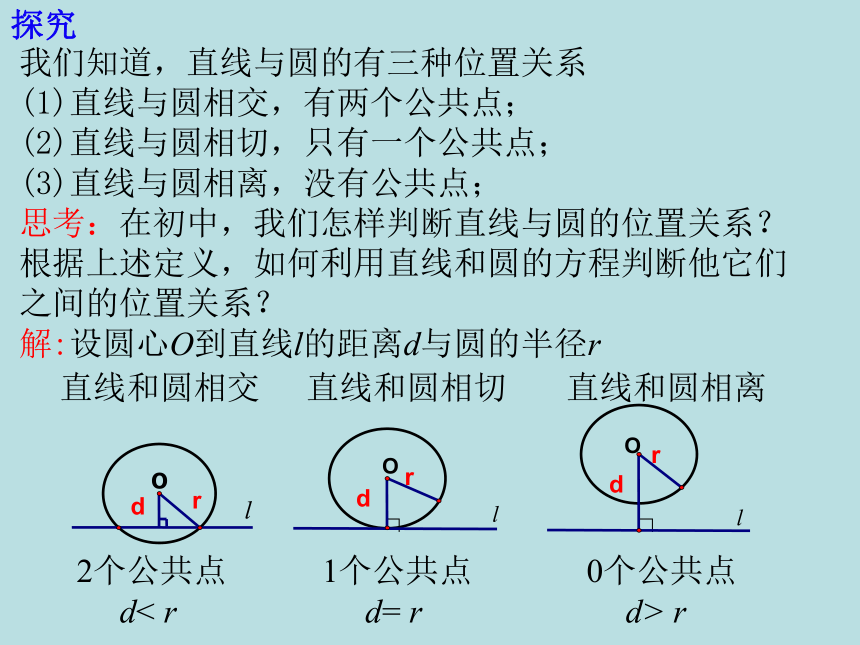
我们知道,直线与圆的有三种位置关系
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点;
思考:在初中,我们怎样判断直线与圆的位置关系?根据上述定义,如何利用直线和圆的方程判断他它们之间的位置关系?
解:设圆心O到直线l的距离d与圆的半径r
探究
r
d
O
∟
r
d
O
∟
r
d
O
直线和圆相交
直线和圆相切
直线和圆相离
d< r
d= r
d> r
2个公共点
1个公共点
0个公共点
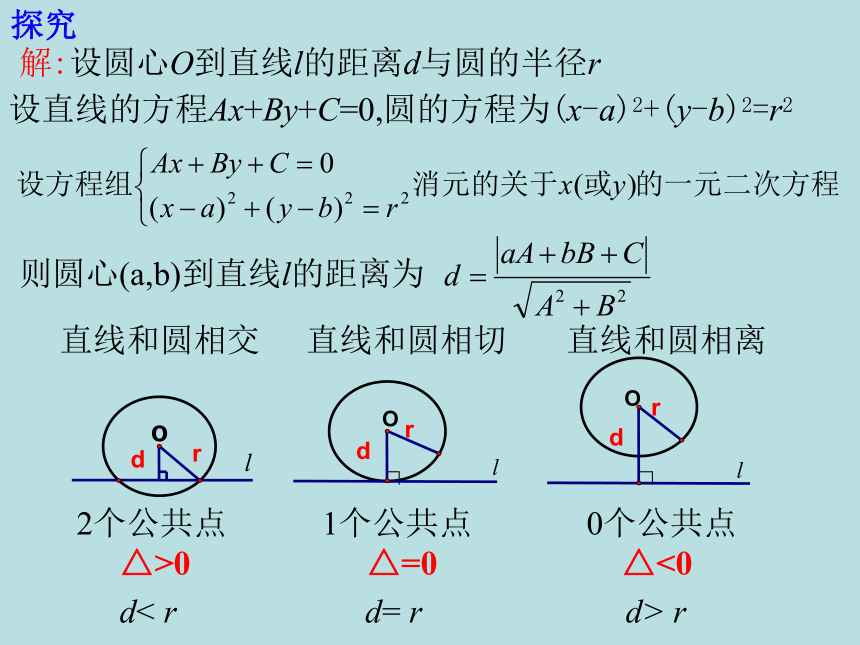
解:设圆心O到直线l的距离d与圆的半径r
探究
r
d
O
∟
r
d
O
∟
r
d
O
直线和圆相交
直线和圆相切
直线和圆相离
d< r
d= r
d> r
2个公共点
1个公共点
0个公共点
△>0
△=0
△<0
设直线的方程Ax+By+C=0,圆的方程为(x-a)2+(y-b)2=r2
则圆心(a,b)到直线l的距离为
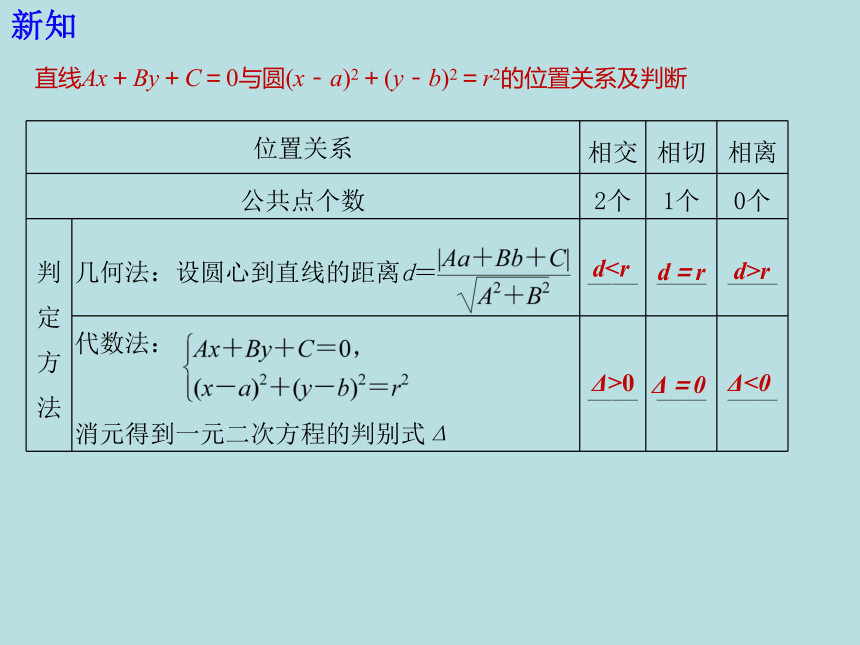
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定方法
几何法:设圆心到直线的距离d=
____
____
____
代数法:
消元得到一元二次方程的判别式Δ
____
____
____
dd=r
d>r
Δ>0
Δ=0
Δ<0
新知
解:联立方程组
消y得 ,解得 x1=1,x2 =2
所以直线l与圆相交,有两个公共点
①
②
把x1,x2代入方程①得到y1 =3 ,y2 =0
所以直线l与圆有两个不同的交点A(1,3),B(2,0)
所以弦长
.
x
y
O
C
A
B
l
例1、如图,已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长。
分析:思路1,将直线与圆的位置关系转化为判断它们的方程组组成的方程组有无实数解、有几个实数解;若相交,可以由方程组解得两交点坐标,利用两点间的距离公式求弦长
例题
.
x
y
O
C
A
B
l
所以,直线l与圆C相交,有两个公共点。
由垂径定理,的|AB|=
解:圆C的方程x2+y2-2y-4=0可化为x2+(y-1)2=5
因此圆心C的坐标为(0,1),半径为
圆心C(0,1)到直线l的距离
垂径定理:垂直于弦的直径平分弦且平分这条弦所对的两条弧
课本P93 练习3
例题
例1、如图,已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长。
分析:思路2,依据圆心到直线的距离与半径的关系,判断直线与圆的位置关系;若相交,则可;利用勾股定理求得弦长
直线与圆位置关系的两种判断方法(1)直线与圆的位置关系的两种判断方法中,
若直线和圆的方程已知或圆心到直线的距离易表达,则用几何法较简单;
若直线或圆的方程中含有参数,且圆心到直线的距离表达较复杂,则用代数法较简单.(2)直线与圆相交,注意半径长、弦心距、弦长的一半构成的直角三角形在解题中的应用.
归纳
练习
已知直线l:2x-y-1=0和圆C:x2+y2-2y-1=0相交于A,B两点.求弦长|AB|.
练习
已知直线l:2x-y-1=0和圆C:x2+y2-2y-1=0相交于A,B两点.求弦长|AB|.
求直线与圆相交时弦长的两种方法
几何法:如图①,直线l与圆C交于A,B两点,设弦心距为d,r圆的半
代数法:联立方程组求交点坐标
归纳
已知圆C:x2+y2=25,求过圆上点P(3,4)的圆的切线方程.
练习
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线的方程
分析:如图,容易知道,点P(2,1)位于圆O:x2+y2=1外,经过圆外一点有两条直线与这个圆相切,我们设切线方程为y-1=k(x-2),k为斜率,由直线与圆相切可求出k的值.
解:当直线的斜率存在时,设切线l的斜率为k,
则切线l的方程为y-1=k(x-2),即x-y+1-2k=0.
由圆心(0,0)到切线l的距离等于圆的半径1,得
解得k=0或k=
因此,所求切线l的方程为y=1,或4x-3y-5=0.
当直线的斜率不存在时,直线与圆不相切
综上,所求切线l的方程为y=1,或4x-3y-5=0.
例题
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线的方程
解法2:当直线的斜率存在时,设切线l的斜率为k,
则切线l的方程为y-1=k(x-2).因为直线l与圆相切,
所以方程组
所以,所求切线l的方程为y=1,或4x-3y-5=0.
消元,得(k2+1)x2+(2k-4k2)x+4k2-4k=0. ①
因为方程①只有一个解,
所以△=4k2(1-2k)2-16k(k2+1)(k-1)=0, 解得k=0或k=
当直线的斜率不存在时,直线与圆不相切
综上,所求切线l的方程为y=1,或4x-3y-5=0.
例题
结合图形解决问题
归纳
练习
已知圆C:x2+y2=25,求过点Q 的圆的切线方程.
例3.如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m).
分析:①圆拱形桥与圆得关系?
②如何求支柱A2P2的高度?
③如何建立平面直角坐标系?
x
y
例题
例3.如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m).
x
y
4
r
r-4
10
解:建立如图所示的直角坐标系,
使线段AB所在直线为x轴,
O为坐标原点,圆心C在y轴上,
则CB=CP=r, CO=r-4,OB=10
所以(r-4)2+102=r2 解得 r=14.5
所以CO=10.5,即b=-10.5
故圆的方程是x2+(y+10.5)2=14.52
当x=2时,代入得y≈3.86
答:支柱A2P2的高度约为3.86m
例题
练习
一座圆弧形拱桥,拱顶离水面2米,水面宽12米,当水面下降1米后,水面宽度为多少?
例4一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内,已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁危险?
分析:先画出示意图,了解小岛中心、轮船、港口的方位和距离,如图,根据题意,建立适当的平面直角坐标系,求出暗礁所在区域的边缘圆的方程,以及轮船返港直线的方程,利用方程判断直线与圆的位置关系,进而确定轮船是否有触礁危险.
例题
例4一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内,已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁危险?
解:以小岛的中心为原点O,东西方向为x轴,
建立如图所示的直角坐标系,为了运算的简便,
我们取10km为单位长度,则港口所在位置的坐
标为(0,3),轮船所在位置的坐标为(4,0).
则环岛暗礁对应得圆得方程为x2+y2=4
轮船航线所在直线方程为 ,即 3x+4y-12=0
联立方程组 消去y得25x2-72x+80=0
由△=(-72)2-4×25×80<0,可知方程组无解.
所以直线l与圆O相离,轮船沿直线返港不会有触礁危险.
思考:你还能用其他方法解决上述问题吗?
例题
解:如图,设轮船开始位于x轴上的A点,港口位于y轴上的B点。
利用平面几何的知识,在RT△AOB中,
原点O到直线AB的距离即为斜边AB上的高
因为|OA|=40km,|OB|=30km,根据勾股定理,
有
设点O到AB的距离为d,则d·|AB|=|OA|·|OB|
所以d=24km,因为24>20,
所以这艘船不必改变航线,不会有触礁的危险。
例4一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内,已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁危险?
例题
用坐标法解决几何问题时,先用坐标和方程表示相应的几何元素:点、直线、圆,将几何问题转化为代数问题;然后通过代数运算解决代数问题;最后解释代数运算结果的几何含义,得到几何问题的结论,这就是用坐标法解决平面几何问题的“三步曲”:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何要素,如点、直线、圆,把平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:把代数运算的结果“翻译”成几何结论.
归纳
小结
1、直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定方法
几何法:设圆心到直线的距离d=
____
____
____
代数法:
消元得到一元二次方程的判别式Δ
____
____
____
dd=r
d>r
Δ>0
Δ=0
Δ<0
2、直线与圆相交,注意半径长、弦心距、弦长的一半构成的直角三角形在解题中的应用.
3、坐标法解决平面几何问题的“三步曲”:建系→运算→翻译
作业
课本P95 练习 2
3、平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
复习
2、圆的一般方程:
1、圆心C(a,b),半径r的圆的标准方程为(x-a)2+(y-b)2=r2
我们知道,直线与圆的有三种位置关系
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,只有一个公共点;
(3)直线与圆相离,没有公共点;
思考:在初中,我们怎样判断直线与圆的位置关系?根据上述定义,如何利用直线和圆的方程判断他它们之间的位置关系?
解:设圆心O到直线l的距离d与圆的半径r
探究
r
d
O
∟
r
d
O
∟
r
d
O
直线和圆相交
直线和圆相切
直线和圆相离
d< r
d= r
d> r
2个公共点
1个公共点
0个公共点
解:设圆心O到直线l的距离d与圆的半径r
探究
r
d
O
∟
r
d
O
∟
r
d
O
直线和圆相交
直线和圆相切
直线和圆相离
d< r
d= r
d> r
2个公共点
1个公共点
0个公共点
△>0
△=0
△<0
设直线的方程Ax+By+C=0,圆的方程为(x-a)2+(y-b)2=r2
则圆心(a,b)到直线l的距离为
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定方法
几何法:设圆心到直线的距离d=
____
____
____
代数法:
消元得到一元二次方程的判别式Δ
____
____
____
d
d>r
Δ>0
Δ=0
Δ<0
新知
解:联立方程组
消y得 ,解得 x1=1,x2 =2
所以直线l与圆相交,有两个公共点
①
②
把x1,x2代入方程①得到y1 =3 ,y2 =0
所以直线l与圆有两个不同的交点A(1,3),B(2,0)
所以弦长
.
x
y
O
C
A
B
l
例1、如图,已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长。
分析:思路1,将直线与圆的位置关系转化为判断它们的方程组组成的方程组有无实数解、有几个实数解;若相交,可以由方程组解得两交点坐标,利用两点间的距离公式求弦长
例题
.
x
y
O
C
A
B
l
所以,直线l与圆C相交,有两个公共点。
由垂径定理,的|AB|=
解:圆C的方程x2+y2-2y-4=0可化为x2+(y-1)2=5
因此圆心C的坐标为(0,1),半径为
圆心C(0,1)到直线l的距离
垂径定理:垂直于弦的直径平分弦且平分这条弦所对的两条弧
课本P93 练习3
例题
例1、如图,已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标及弦长。
分析:思路2,依据圆心到直线的距离与半径的关系,判断直线与圆的位置关系;若相交,则可;利用勾股定理求得弦长
直线与圆位置关系的两种判断方法(1)直线与圆的位置关系的两种判断方法中,
若直线和圆的方程已知或圆心到直线的距离易表达,则用几何法较简单;
若直线或圆的方程中含有参数,且圆心到直线的距离表达较复杂,则用代数法较简单.(2)直线与圆相交,注意半径长、弦心距、弦长的一半构成的直角三角形在解题中的应用.
归纳
练习
已知直线l:2x-y-1=0和圆C:x2+y2-2y-1=0相交于A,B两点.求弦长|AB|.
练习
已知直线l:2x-y-1=0和圆C:x2+y2-2y-1=0相交于A,B两点.求弦长|AB|.
求直线与圆相交时弦长的两种方法
几何法:如图①,直线l与圆C交于A,B两点,设弦心距为d,r圆的半
代数法:联立方程组求交点坐标
归纳
已知圆C:x2+y2=25,求过圆上点P(3,4)的圆的切线方程.
练习
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线的方程
分析:如图,容易知道,点P(2,1)位于圆O:x2+y2=1外,经过圆外一点有两条直线与这个圆相切,我们设切线方程为y-1=k(x-2),k为斜率,由直线与圆相切可求出k的值.
解:当直线的斜率存在时,设切线l的斜率为k,
则切线l的方程为y-1=k(x-2),即x-y+1-2k=0.
由圆心(0,0)到切线l的距离等于圆的半径1,得
解得k=0或k=
因此,所求切线l的方程为y=1,或4x-3y-5=0.
当直线的斜率不存在时,直线与圆不相切
综上,所求切线l的方程为y=1,或4x-3y-5=0.
例题
例2.过点P(2,1)作圆O:x2+y2=1的切线l,求切线的方程
解法2:当直线的斜率存在时,设切线l的斜率为k,
则切线l的方程为y-1=k(x-2).因为直线l与圆相切,
所以方程组
所以,所求切线l的方程为y=1,或4x-3y-5=0.
消元,得(k2+1)x2+(2k-4k2)x+4k2-4k=0. ①
因为方程①只有一个解,
所以△=4k2(1-2k)2-16k(k2+1)(k-1)=0, 解得k=0或k=
当直线的斜率不存在时,直线与圆不相切
综上,所求切线l的方程为y=1,或4x-3y-5=0.
例题
结合图形解决问题
归纳
练习
已知圆C:x2+y2=25,求过点Q 的圆的切线方程.
例3.如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m).
分析:①圆拱形桥与圆得关系?
②如何求支柱A2P2的高度?
③如何建立平面直角坐标系?
x
y
例题
例3.如图是某圆拱形桥一孔圆拱的示意图.圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m).
x
y
4
r
r-4
10
解:建立如图所示的直角坐标系,
使线段AB所在直线为x轴,
O为坐标原点,圆心C在y轴上,
则CB=CP=r, CO=r-4,OB=10
所以(r-4)2+102=r2 解得 r=14.5
所以CO=10.5,即b=-10.5
故圆的方程是x2+(y+10.5)2=14.52
当x=2时,代入得y≈3.86
答:支柱A2P2的高度约为3.86m
例题
练习
一座圆弧形拱桥,拱顶离水面2米,水面宽12米,当水面下降1米后,水面宽度为多少?
例4一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内,已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁危险?
分析:先画出示意图,了解小岛中心、轮船、港口的方位和距离,如图,根据题意,建立适当的平面直角坐标系,求出暗礁所在区域的边缘圆的方程,以及轮船返港直线的方程,利用方程判断直线与圆的位置关系,进而确定轮船是否有触礁危险.
例题
例4一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内,已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁危险?
解:以小岛的中心为原点O,东西方向为x轴,
建立如图所示的直角坐标系,为了运算的简便,
我们取10km为单位长度,则港口所在位置的坐
标为(0,3),轮船所在位置的坐标为(4,0).
则环岛暗礁对应得圆得方程为x2+y2=4
轮船航线所在直线方程为 ,即 3x+4y-12=0
联立方程组 消去y得25x2-72x+80=0
由△=(-72)2-4×25×80<0,可知方程组无解.
所以直线l与圆O相离,轮船沿直线返港不会有触礁危险.
思考:你还能用其他方法解决上述问题吗?
例题
解:如图,设轮船开始位于x轴上的A点,港口位于y轴上的B点。
利用平面几何的知识,在RT△AOB中,
原点O到直线AB的距离即为斜边AB上的高
因为|OA|=40km,|OB|=30km,根据勾股定理,
有
设点O到AB的距离为d,则d·|AB|=|OA|·|OB|
所以d=24km,因为24>20,
所以这艘船不必改变航线,不会有触礁的危险。
例4一个小岛的周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内,已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁危险?
例题
用坐标法解决几何问题时,先用坐标和方程表示相应的几何元素:点、直线、圆,将几何问题转化为代数问题;然后通过代数运算解决代数问题;最后解释代数运算结果的几何含义,得到几何问题的结论,这就是用坐标法解决平面几何问题的“三步曲”:
第一步:建立适当的平面直角坐标系,用坐标和方程表示问题中的几何要素,如点、直线、圆,把平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:把代数运算的结果“翻译”成几何结论.
归纳
小结
1、直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定方法
几何法:设圆心到直线的距离d=
____
____
____
代数法:
消元得到一元二次方程的判别式Δ
____
____
____
d
d>r
Δ>0
Δ=0
Δ<0
2、直线与圆相交,注意半径长、弦心距、弦长的一半构成的直角三角形在解题中的应用.
3、坐标法解决平面几何问题的“三步曲”:建系→运算→翻译
作业
课本P95 练习 2
