2.5.2圆与圆的位置关系 课件(共17张PPT)——2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 2.5.2圆与圆的位置关系 课件(共17张PPT)——2020-2021学年高二上学期数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 223.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 10:20:35 | ||
图片预览




文档简介
2.5.2圆与圆的位置关系
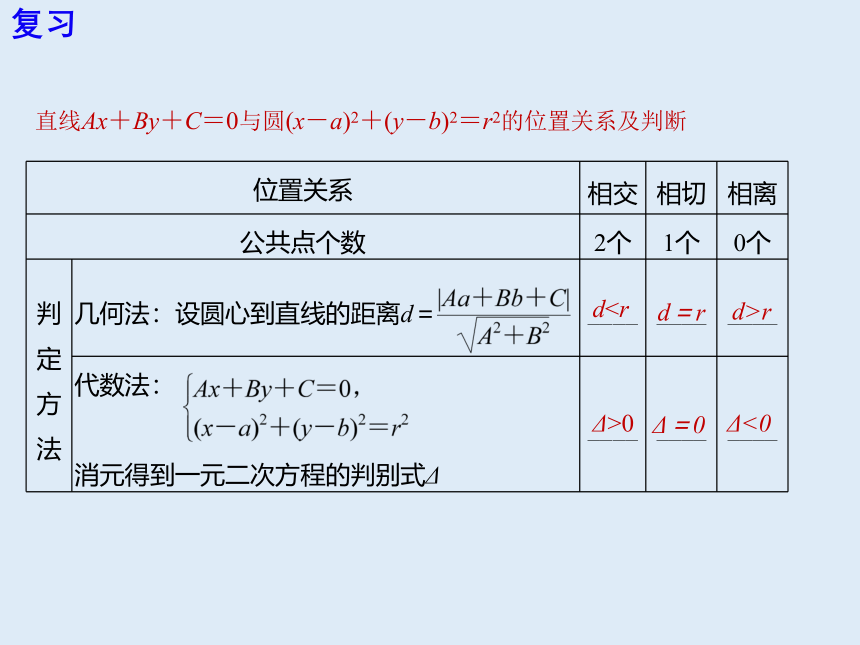
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定方法
几何法:设圆心到直线的距离d=
____
____
____
代数法:
消元得到一元二次方程的判别式Δ
____
____
____
dd=r
d>r
Δ>0
Δ=0
Δ<0
复习
探究
两个圆之间存在以下三种位置关系:
(1)两圆相交,有两个公共点
(2)两圆相切,包括外切与内切,只有一个公共点
(3)两圆相离,包括外离与内含,没有公共点
思考:
类比运用直线和圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的关系?
解:设两圆的一般方程为C1:x2+y2+D1x+E1y+F1=0(D12+E12-4F1>0),C2:x2+y2+D2x+E2y+F2=0(D22+E22-4F2>0),联立方程,则方程组解的个数与两圆的位置关系如下:
{5940675A-B579-460E-94D1-54222C63F5DA}方程组解的个数
2组
1组
0组
两圆的公共点个数
2个
1个
0个
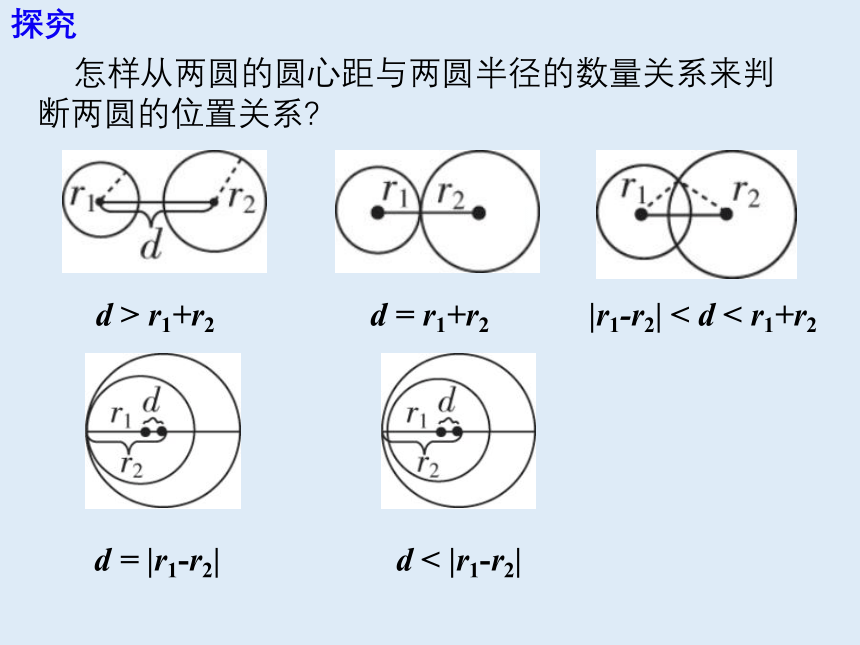
探究
怎样从两圆的圆心距与两圆半径的数量关系来判断两圆的位置关系?
d > r1+r2
d = r1+r2
|r1-r2| < d < r1+r2
d = |r1-r2|
d < |r1-r2|
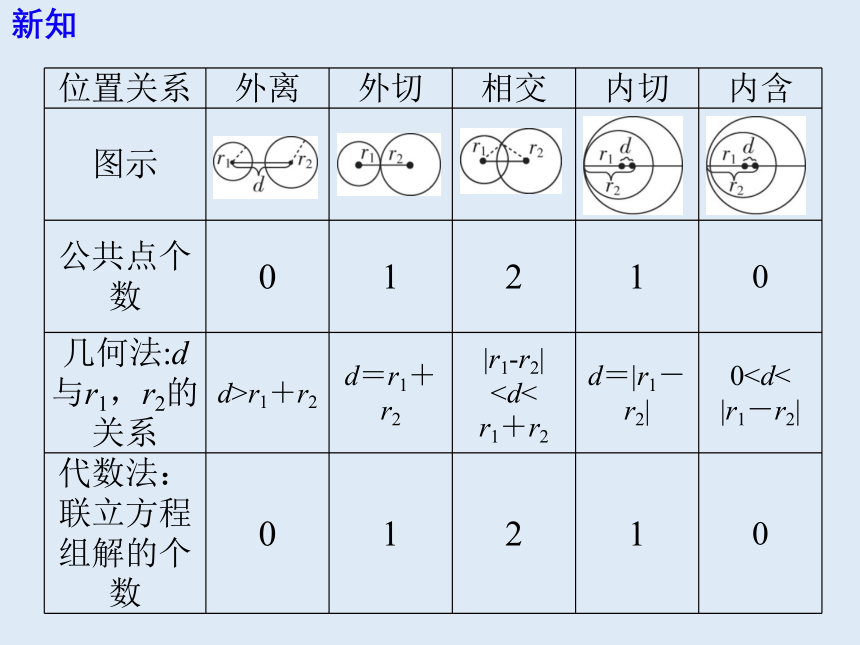
新知
{5940675A-B579-460E-94D1-54222C63F5DA}位置关系
外离
外切
相交
内切
内含
图示
公共点个数
0
1
2
1
0
几何法:d与r1,r2的关系
d>r1+r2
d=r1+r2
|r1-r2|
r1+r2
d=|r1-r2|
0|r1-r2|
代数法:联立方程组解的个数
0
1
2
1
0
例5 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
解:
∴
∴
例题
①
②
①-②化简得:x+2y-1=0
代入①化简得x2-2x-3=0
例5 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
课本P98练习1
例题
归纳
1、几何法:判断两圆的位置关系的步骤:①化成圆的标准方程,写出圆心和半径;②计算两圆圆心的距离d;③通过d,r1+r2,|r1-r2|的关系来判断两圆的位置关系或求参数的范围,必要时可借助于图形,数形结合. 2、如果判断两圆相交并求交点坐标时,必须求方程组的解,这样用方程组解的个数判断两圆位置关系可起到一举两得的效果.
(1)已知两圆的半径分别为1和5,若两圆相交,则圆心距d的取值范围是________.
(2)已知圆O1与圆O2的方程分别为(x-1)2+y2=1,(x+1)2+y2=r2(r>1),若两圆相交,则r的取值范围是________.
练习
①
②
①-②化简得:x+2y-1=0 ③
代入①化简得x2-2x-3=0
例5 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
例题
C1
C2
A
B
O
两圆的交点A、B坐标是方程组的解,则A、B坐标满足方程③,③为两圆相交弦所在直线方程
求两圆相交弦所在直线方程的方法:两圆方程相减
求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
练习
解:联立两圆的方程得方程组
x2+y2-2x+10y-24=0
x2+y2+2x+2y-8=0
两式相减得x-2y+4=0,
此即为两圆公共弦所在直线的方程.
求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
练习
解:联立两圆的方程得方程组
x2+y2-2x+10y-24=0
x2+y2+2x+2y-8=0
两式相减得x-2y+4=0,
此即为两圆公共弦所在直线的方程.
归纳
公共弦长的求法(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
例6 已知圆O的直径AB=4,动点M与点A的距离是它与点B的距离的 倍。试探究点M的轨迹,并判断该轨迹与圆O的位置关系。
解:以线段AB的中点O为原点,AB所在直线为x轴,
线段AB的垂直平分线为y轴,建立平面直角坐标系
由AB=4可得A(-2,0),B(2,0)
设点M(x,y)
∵|MA|= |MB|
所以
化简得 ,即(x-6)2+y2=32
故点M的轨迹是以P(6,0)为圆心,半径为4 的圆
因为圆心距|PO|=6,两圆半径r1=2,r2=4
又∵r2-r1<|PO|例题
求轨迹方程的常用方法(二)(1)代入法(2)直接法:根据题目的条件,建立适当的平面直角坐标系,设出动点坐标,并找出动点坐标所满足的关系式.即“建设限代化”
归纳
1.圆与圆位置关系的判定;
(1)几何法:比较d与r
(2)坐标法:方程组根的个数
2.相交两圆的几何性质.
(1)公共弦所在直线方程
(2)公共弦弦长
3.求轨迹方程的常用方法
(1)直接法
(2)代入法
小结
作业
课本P98练习2
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定方法
几何法:设圆心到直线的距离d=
____
____
____
代数法:
消元得到一元二次方程的判别式Δ
____
____
____
d
d>r
Δ>0
Δ=0
Δ<0
复习
探究
两个圆之间存在以下三种位置关系:
(1)两圆相交,有两个公共点
(2)两圆相切,包括外切与内切,只有一个公共点
(3)两圆相离,包括外离与内含,没有公共点
思考:
类比运用直线和圆的方程,研究直线与圆的位置关系的方法,如何利用圆的方程,判断它们之间的关系?
解:设两圆的一般方程为C1:x2+y2+D1x+E1y+F1=0(D12+E12-4F1>0),C2:x2+y2+D2x+E2y+F2=0(D22+E22-4F2>0),联立方程,则方程组解的个数与两圆的位置关系如下:
{5940675A-B579-460E-94D1-54222C63F5DA}方程组解的个数
2组
1组
0组
两圆的公共点个数
2个
1个
0个
探究
怎样从两圆的圆心距与两圆半径的数量关系来判断两圆的位置关系?
d > r1+r2
d = r1+r2
|r1-r2| < d < r1+r2
d = |r1-r2|
d < |r1-r2|
新知
{5940675A-B579-460E-94D1-54222C63F5DA}位置关系
外离
外切
相交
内切
内含
图示
公共点个数
0
1
2
1
0
几何法:d与r1,r2的关系
d>r1+r2
d=r1+r2
|r1-r2|
d=|r1-r2|
0
代数法:联立方程组解的个数
0
1
2
1
0
例5 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
解:
∴
∴
例题
①
②
①-②化简得:x+2y-1=0
代入①化简得x2-2x-3=0
例5 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
课本P98练习1
例题
归纳
1、几何法:判断两圆的位置关系的步骤:①化成圆的标准方程,写出圆心和半径;②计算两圆圆心的距离d;③通过d,r1+r2,|r1-r2|的关系来判断两圆的位置关系或求参数的范围,必要时可借助于图形,数形结合. 2、如果判断两圆相交并求交点坐标时,必须求方程组的解,这样用方程组解的个数判断两圆位置关系可起到一举两得的效果.
(1)已知两圆的半径分别为1和5,若两圆相交,则圆心距d的取值范围是________.
(2)已知圆O1与圆O2的方程分别为(x-1)2+y2=1,(x+1)2+y2=r2(r>1),若两圆相交,则r的取值范围是________.
练习
①
②
①-②化简得:x+2y-1=0 ③
代入①化简得x2-2x-3=0
例5 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,试判断圆C1与圆C2的位置关系.
例题
C1
C2
A
B
O
两圆的交点A、B坐标是方程组的解,则A、B坐标满足方程③,③为两圆相交弦所在直线方程
求两圆相交弦所在直线方程的方法:两圆方程相减
求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
练习
解:联立两圆的方程得方程组
x2+y2-2x+10y-24=0
x2+y2+2x+2y-8=0
两式相减得x-2y+4=0,
此即为两圆公共弦所在直线的方程.
求两圆x2+y2-2x+10y-24=0和x2+y2+2x+2y-8=0的公共弦所在直线的方程及公共弦长.
练习
解:联立两圆的方程得方程组
x2+y2-2x+10y-24=0
x2+y2+2x+2y-8=0
两式相减得x-2y+4=0,
此即为两圆公共弦所在直线的方程.
归纳
公共弦长的求法(1)代数法:将两圆的方程联立,解出交点坐标,利用两点间的距离公式求出弦长.(2)几何法:求出公共弦所在直线的方程,利用圆的半径、半弦长、弦心距构成的直角三角形,根据勾股定理求解.
例6 已知圆O的直径AB=4,动点M与点A的距离是它与点B的距离的 倍。试探究点M的轨迹,并判断该轨迹与圆O的位置关系。
解:以线段AB的中点O为原点,AB所在直线为x轴,
线段AB的垂直平分线为y轴,建立平面直角坐标系
由AB=4可得A(-2,0),B(2,0)
设点M(x,y)
∵|MA|= |MB|
所以
化简得 ,即(x-6)2+y2=32
故点M的轨迹是以P(6,0)为圆心,半径为4 的圆
因为圆心距|PO|=6,两圆半径r1=2,r2=4
又∵r2-r1<|PO|
求轨迹方程的常用方法(二)(1)代入法(2)直接法:根据题目的条件,建立适当的平面直角坐标系,设出动点坐标,并找出动点坐标所满足的关系式.即“建设限代化”
归纳
1.圆与圆位置关系的判定;
(1)几何法:比较d与r
(2)坐标法:方程组根的个数
2.相交两圆的几何性质.
(1)公共弦所在直线方程
(2)公共弦弦长
3.求轨迹方程的常用方法
(1)直接法
(2)代入法
小结
作业
课本P98练习2
