2020-2021学年湖南省娄底市娄星区八年级(下)期末数学试卷 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年湖南省娄底市娄星区八年级(下)期末数学试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1018.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 05:56:26 | ||
图片预览



文档简介
2020-2021学年湖南省娄底市娄星区八年级(下)期末数学试卷
一、选择题(每小题3分,共12小题)
1.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.在下列函数中:①y=﹣8x;②;③;④y=﹣8x2+5;⑤y=﹣0.5x﹣1,一次函数有( )
A.1个 B.2个 C.3个 D.4个
3.在下列长度的四组线段中,不能组成直角三角形的是( )
A.a=5,b=12,c=13 B.,c=2
C.a:b:c=3:4:5 D.a=4,b=5,c=6
4.下列对于一次函数y=﹣3x+2的描述错误的是( )
A.y随x的增大而减小
B.图象经过点(2,4)
C.图象与直线y=3x相交
D.图象可由直线y=﹣3x向上平移2个单位得到
5.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量其中三个角是否都为直角
6.点A(﹣2,y1),B(3,y2)是一次函数y=﹣2x+1图象上的两点,则( )
A.y1>y2 B.y1≥y2 C.y1<y2 D.y1≤y2
7.如图,若在某棋盘上建立直角坐标系,使“将”位于点(2,﹣1),则“炮”位于点( )
A.(﹣1,2) B.(﹣1,3) C.(﹣2,3) D.(﹣2,2)
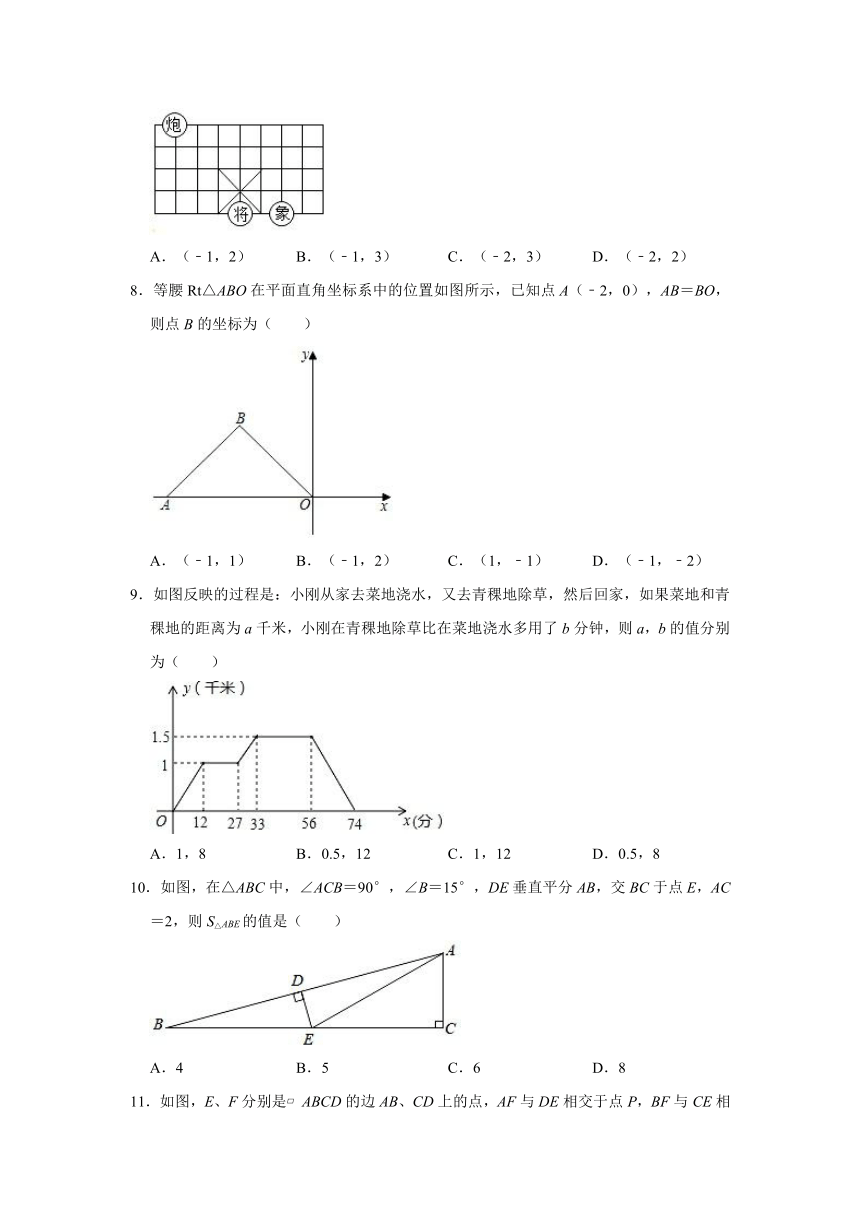
8.等腰Rt△ABO在平面直角坐标系中的位置如图所示,已知点A(﹣2,0),AB=BO,则点B的坐标为( )
A.(﹣1,1) B.(﹣1,2) C.(1,﹣1) D.(﹣1,﹣2)
9.如图反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为a千米,小刚在青稞地除草比在菜地浇水多用了b分钟,则a,b的值分别为( )
A.1,8 B.0.5,12 C.1,12 D.0.5,8
10.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AC=2,则S△ABE的值是( )
A.4 B.5 C.6 D.8
11.如图,E、F分别是?ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15,S△BQC=25,则阴影部分的面积为( )
A.40 B.45 C.50 D.55
12.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列四个结论:
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④S△ACD:S△ACB=1:3.
其中正确的有( )
A.只有①②③ B.只有①②④ C.只有①③④ D.①②③④
二、填空题(每小题3分,满分18分)
13.已知正n边形的一个内角为140°,则n等于 .
14.将一组有80个数据的样本分成6个组,第1~4组的频数分别是14,13,18,11,第5组的频率是0.2,则第6组的频数是 .
15.若一次函数y=kx﹣3(k为常数,k≠0)的图象经过第二、三、四象限,则k的值可以是 .(写出一个即可)
16.如图,CD是Rt△ABC的中线,∠ACB=90°,∠ABC=25°,则∠ADC的度数是 .
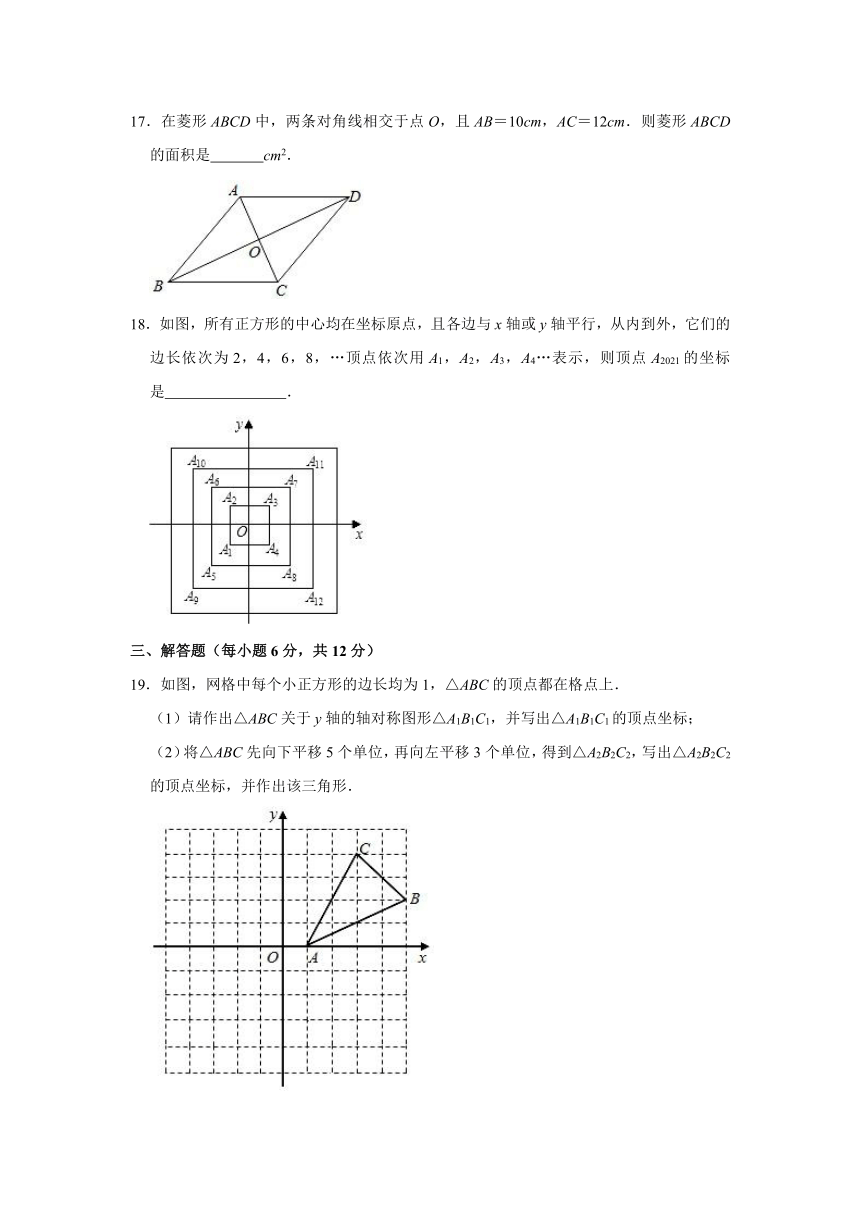
17.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是 cm2.
18.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…顶点依次用A1,A2,A3,A4…表示,则顶点A2021的坐标是 .
三、解答题(每小题6分,共12分)
19.如图,网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)请作出△ABC关于y轴的轴对称图形△A1B1C1,并写出△A1B1C1的顶点坐标;
(2)将△ABC先向下平移5个单位,再向左平移3个单位,得到△A2B2C2,写出△A2B2C2的顶点坐标,并作出该三角形.
20.如图,已知∠B=∠ADC=90°,DC=7,AB=20,BC=15,求AD的长.
四、解答题(每小题8分,共16分)
21.某班进行了一次数学考试,将成绩绘制成了不完整的频数分布直方图和频数分布表:
成绩 频数(人数) 频率
50≤x<60 4 0.08
60≤x<70 8 0.16
70≤x<80 20 0.4
80≤x<90 a 0.3
90≤x<100 3 b
(1)求频数分布表中a和b的值;
(2)将频数分布直方图补充完整;
(3)若成绩不低于80分为优秀,则该班本次数学考试的优秀率是多少?
22.某高铁修建过程中需要经过一座大山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D三点共线)处同时施工.测得∠CAB=30°,∠ABD=105°,AB=8km,求BD的长.(结果精确到0.1km,,)
五、应用题(每小题9分,共2小题,满分18分)
23.疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购2000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买A、B、C三种型号的口罩,其单价(元/袋)分别为30、35、40,若购买B型口罩的数量是A型的2倍,设购买A型口罩x袋,该企业购买口罩的总费用为y元.
(1)请求出y与x的函数关系式;
(2)已知口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,当购买A型口罩多少袋时购买口罩的总费用最少?并求最少总费用.
24.如图,在Rt△ABC中,∠ACB=90°,点E、F分别是AB、BC的中点,点D是CA延长线上的一点,且,连接DE、AF.
(1)求证:四边形ADEF是平行四边形;
(2)若四边形ADEF的周长是14cm,AC的长为4cm,求四边形ADEF的面积.
六、综合与探究(每小题10分,共2小题,满分20分)
25.如图,直线l1与l2相交于点P,点P横坐标为﹣4,l1的表达式为,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
(1)求点B的坐标和直线l2的表达式;
(2)若点M为直线l2上一点,且,求M的坐标.
26.如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,连接CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,请用含x的代数式表示△FCG的面积.
参考答案
一、选择题(每小题3分,共12小题,满分36分。每小题给出的四个选项中,只有一个选项是符合题目要求的,请把表示正确答案的字母填入下表中对应的题号下.)
1.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
解:A.是轴对称图形,不是中心对称图形,故此选项不合题意;
B.既是轴对称图形,又是中心对称图形,故此选项符合题意;
C.是轴对称图形,不是中心对称图形,故此选项不合题意;
D.是轴对称图形,不是中心对称图形,故此选项不合题意;
故选:B.
2.在下列函数中:①y=﹣8x;②;③;④y=﹣8x2+5;⑤y=﹣0.5x﹣1,一次函数有( )
A.1个 B.2个 C.3个 D.4个
解:∵一次函数的解析式为y=kx+b(k≠0),
y=﹣8x,y=x+1,y=﹣0.5x﹣1符合一次函数解析式形式,
∴一次函数有①②⑤,
故选:C.
3.在下列长度的四组线段中,不能组成直角三角形的是( )
A.a=5,b=12,c=13 B.,c=2
C.a:b:c=3:4:5 D.a=4,b=5,c=6
解:A、52+122=132,能构成直角三角形,故本选项不符合题意;
B、()2+()2=22,能构成直角三角形,故本选项不符合题意;
C、(3x)2+(4x)2=(5x)2,能构成直角三角形,故本选项不符合题意;
D、52+42≠62,不能构成直角三角形,故本选项符合题意;
故选:D.
4.下列对于一次函数y=﹣3x+2的描述错误的是( )
A.y随x的增大而减小
B.图象经过点(2,4)
C.图象与直线y=3x相交
D.图象可由直线y=﹣3x向上平移2个单位得到
解:A、由于一次函数y=﹣3x+2中的k=﹣3<0,所以y随x的增大而减小,故不符合题意.
B、令x=2,则y=﹣6+2=﹣4,即一次函数y=﹣3x+2图象经过点(2,﹣4),故符合题意.
C、直线y=﹣3x+2中的k=﹣3,直线y=3x中的k=3,故两直线不平行,则相交,故不符合题意.
D、直线y=﹣3x向上平移2个单位得到y=﹣3x+2,故不符合题意.
故选:B.
5.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量其中三个角是否都为直角
解:A、对角线是否相互平分,能判定平行四边形;
B、两组对边是否分别相等,能判定平行四边形;
C、对角线相等的四边形不一定是矩形,不能判定形状;
D、其中四边形中三个角都为直角,能判定矩形.
故选:D.
6.点A(﹣2,y1),B(3,y2)是一次函数y=﹣2x+1图象上的两点,则( )
A.y1>y2 B.y1≥y2 C.y1<y2 D.y1≤y2
解:∵一次函数y=﹣2x+1的图象y随着x的增大而减小,
又∵﹣2<3
∴y1>y2,
故选:A.
7.如图,若在某棋盘上建立直角坐标系,使“将”位于点(2,﹣1),则“炮”位于点( )
A.(﹣1,2) B.(﹣1,3) C.(﹣2,3) D.(﹣2,2)
解:如图所示:“炮”位于点(﹣1,3).
故选:B.
8.等腰Rt△ABO在平面直角坐标系中的位置如图所示,已知点A(﹣2,0),AB=BO,则点B的坐标为( )
A.(﹣1,1) B.(﹣1,2) C.(1,﹣1) D.(﹣1,﹣2)
解:如图,过点B作BE⊥AO于E,
∵点A(﹣2,0),
∴AO=2,
∵AB=BO,∠ABO=90°,
∴AE=BE=EO=1,
∴点B(﹣1,1),
故选:A.
9.如图反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为a千米,小刚在青稞地除草比在菜地浇水多用了b分钟,则a,b的值分别为( )
A.1,8 B.0.5,12 C.1,12 D.0.5,8
解:此函数大致可分以下几个阶段:
①0﹣12分种,小刚从家走到菜地;
②12﹣27分钟,小刚在菜地浇水;
③27﹣33分钟,小刚从菜地走到青稞地;
④33﹣56分钟,小刚在青稞地除草;
⑤56﹣74分钟,小刚从青稞地回到家;
综合上面的分析得:由③的过程知,a=1.5﹣1=0.5千米;
由②、④的过程知b=(56﹣33)﹣(27﹣12)=8分钟.
故选:D.
10.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AC=2,则S△ABE的值是( )
A.4 B.5 C.6 D.8
解:∵DE垂直平分AB,
∴AE=BE,
∴∠EAB=∠B=15°,
∴∠AEC=∠B+∠BAE=30°,
∵∠ACE=90°,AC=2,
∴AE=BE=2AC=4,
∴S△ABE=BE?AC=,
故选:A.
11.如图,E、F分别是?ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15,S△BQC=25,则阴影部分的面积为( )
A.40 B.45 C.50 D.55
解:如图,连接E、F两点,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=15,S△BQC=25,
∴S四边形EPFQ=S△APD+S△BQC=15+25=40,
故选:A.
12.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列四个结论:
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④S△ACD:S△ACB=1:3.
其中正确的有( )
A.只有①②③ B.只有①②④ C.只有①③④ D.①②③④
解:根据作图方法可得AD是∠BAC的平分线,故①正确;
∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=30°,
∴∠ADC=60°,故②正确;
∵∠B=30°,∠DAB=30°,
∴AD=DB,
∴点D在AB的中垂线上,故③正确;
∵∠CAD=30°,
∴CD=AD,
∵AD=DB,
∴CD=DB,
∴CD=CB,
S△ACD=CD?AC,S△ACB=CB?AC,
∴S△ACD:S△ACB=1:3,故④正确,
故选:D.
二、填空题(每小题3分,满分18分)
13.已知正n边形的一个内角为140°,则n等于 9 .
解:法一、由题意,得(n﹣2)×180=140n,
解得n=9.
故答案为:9.
法二、∵正n边形的一个内角为140°,其外角都为40°.
由于多边形的外角和为360°,
所以n为:360÷40=9.
故答案为:9.
14.将一组有80个数据的样本分成6个组,第1~4组的频数分别是14,13,18,11,第5组的频率是0.2,则第6组的频数是 8 .
解:∵第5组的频数为80×0.2=16,
∴第6组的频数为80﹣(14+13+18+11+16)=8,
故答案为:8.
15.若一次函数y=kx﹣3(k为常数,k≠0)的图象经过第二、三、四象限,则k的值可以是 ﹣1(答案不唯一) .(写出一个即可)
解:因为一次函数y=kx﹣3(k是常数,k≠0)的图象经过第二、三、四象限,
所以k<0,﹣3<0,
所以k可以取﹣1,
故答案为:﹣1(答案不唯一).
16.如图,CD是Rt△ABC的中线,∠ACB=90°,∠ABC=25°,则∠ADC的度数是 50° .
解:∵CD是Rt△ABC的中线,∠ACB=90°,
∴DC=DB,
∴∠DCB=∠ABC=25°,
∴∠ADC=∠DCB+∠ABC=50°,
故答案是:50°.
17.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是 96 cm2.
解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC=6cm,OB=OD,
∴OB===8(cm),
∴BD=2OB=16cm,
∴S菱形ABCD=AC?BD=×12×16=96(cm2).
故答案为:96.
18.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…顶点依次用A1,A2,A3,A4…表示,则顶点A2021的坐标是 (﹣506,﹣506) .
解:观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,
∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数),
∵2021=505×4+1,
∴A2021(﹣506,﹣506).
故答案为:(﹣506,﹣506).
三、解答题(每小题6分,共12分)
19.如图,网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)请作出△ABC关于y轴的轴对称图形△A1B1C1,并写出△A1B1C1的顶点坐标;
(2)将△ABC先向下平移5个单位,再向左平移3个单位,得到△A2B2C2,写出△A2B2C2的顶点坐标,并作出该三角形.
解:(1)△A1B1C1如图所示:
A1 (﹣1,0),B1 (﹣5,2)C1,(﹣3,4);
(2)△A2B2C2如图所示:
A2 (﹣2,﹣5),B2 (2,﹣3),C2 (0,﹣1).
20.如图,已知∠B=∠ADC=90°,DC=7,AB=20,BC=15,求AD的长.
解:连接AC,在Rt△ABC中,AB=20,BC=15,
∴AC2=AB2+BC2=202+152=625,
在Rt△ADC中,DC=7,
∴AD=.
四、解答题(每小题8分,共16分)
21.某班进行了一次数学考试,将成绩绘制成了不完整的频数分布直方图和频数分布表:
成绩 频数(人数) 频率
50≤x<60 4 0.08
60≤x<70 8 0.16
70≤x<80 20 0.4
80≤x<90 a 0.3
90≤x<100 3 b
(1)求频数分布表中a和b的值;
(2)将频数分布直方图补充完整;
(3)若成绩不低于80分为优秀,则该班本次数学考试的优秀率是多少?
解:(1)某班的学生有:4÷0.08=50(人),
a=50×0.3=15,b=3÷50=0.06,
答:频数分布表中a和b的值分别为15,0.06;
(2)补全频数分布直方图如图所示;
(3)成绩不低于80分的频率为0.3+0.06=0.36,
∴该班本次数学考试的优秀率是0.36=36%,
答:该班本次数学考试的优秀率是36%.
22.某高铁修建过程中需要经过一座大山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D三点共线)处同时施工.测得∠CAB=30°,∠ABD=105°,AB=8km,求BD的长.(结果精确到0.1km,,)
解:如图,过点B作BE⊥AD于点E,
∵∠EAB=30°,AB=8km,
∴BE=,∠ABE=60°.
又∵∠ABD=105°,
∴∠DBE=∠ABD﹣∠ABE=45°.
∴Rt△BDE是等腰直角三角形.
∴BD=
=
=4
=5.656
≈5.7(km).
答:BD长约为5.7km.
五、应用题(每小题9分,共2小题,满分18分)
23.疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购2000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买A、B、C三种型号的口罩,其单价(元/袋)分别为30、35、40,若购买B型口罩的数量是A型的2倍,设购买A型口罩x袋,该企业购买口罩的总费用为y元.
(1)请求出y与x的函数关系式;
(2)已知口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,当购买A型口罩多少袋时购买口罩的总费用最少?并求最少总费用.
解:(1)根据题意得购买B型口罩为2x袋,购买C型口罩(2000﹣x﹣2x)袋,
∴y=30x+35×2x+40×(2000﹣x﹣2x)=80000﹣20x;
(2)依题意,得:x≤2000﹣x﹣2x,
解得:x≤500.
∵k=﹣20<0,
∴y随x的增大而减小,
当x=500时,y取得最小值,y最小=80000﹣20×500=70000(元).
答:当购买A型口罩500袋时,购买口罩的总费用最少,最少总费用为70000元.
24.如图,在Rt△ABC中,∠ACB=90°,点E、F分别是AB、BC的中点,点D是CA延长线上的一点,且,连接DE、AF.
(1)求证:四边形ADEF是平行四边形;
(2)若四边形ADEF的周长是14cm,AC的长为4cm,求四边形ADEF的面积.
【解答】(1)证明:∵点E、F分别是AB、BC的中点,
∴EF是△ABC的中位线,
∴EF=AC,EF∥AC,
∵AD=AC,
∴EF=AD,
∵EF∥AD,
∴四边形ADEF是平行四边形;
(2)解:∵四边形ADEF是平行四边形,四边形ADEF的周长是14cm,
∴AD=EF,AF=DE,AD+AF=7cm,
∵AC的长为4cm,
∴AD=AC=×4=2(cm),
∴AF=7﹣AD=7﹣2=5(cm),
在Rt△ACF中,由勾股定理得:CF===3(cm),
∴四边形ADEF的面积=AD?CF=2×3=6(cm2).
六、综合与探究(每小题10分,共2小题,满分20分)
25.如图,直线l1与l2相交于点P,点P横坐标为﹣4,l1的表达式为,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
(1)求点B的坐标和直线l2的表达式;
(2)若点M为直线l2上一点,且,求M的坐标.
解:(1)当x=0时,y=x+3=3,
则A(0,3),
而点A与点B恰好关于x轴对称,
所以B点坐标为(0,﹣3);
当x=﹣4时,y=x+3=1,
则P(﹣4,1),
设直线l2的表达式为y=kx+b,
把B(0,﹣3),P(﹣4,1)分别代入得,
解得,
所以直线l2的表达式为y=﹣x﹣3;
(2)设M点的横坐标为t,则它的纵坐标为﹣t﹣3,
因为:S△PAB=×[3﹣(﹣3)]×|﹣4|=12,
S△MAB=×[3﹣(﹣3)]×|t|=3|t|,
,
所以有:3|t|=×12,
解得:t=2或﹣2,
所以M点的坐标为(2,﹣5)或(﹣2,﹣1).
26.如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,连接CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,请用含x的代数式表示△FCG的面积.
【解答】证明:(1)∵四边形EFGH为菱形,
∴EH=HG,
在Rt△AHE和Rt△DGH中,
,
∴Rt△AHE≌Rt△DGH(HL),
∴∠AHE=∠DGH,
又∵∠DGH+∠DHG=90°,
∴∠AHE+∠DHG=90°,
则∠GHE=90°.
所以菱形EFGH为正方形;
(2)如图,过点F作FM⊥DC交DC所在直线于M,连接GE.
∵AB∥CD,
∴∠AEG=∠MGE,
∵HE∥GF,
∴∠HEG=∠FGE.
∴∠HEA=∠FGM,
在△AHE和△MFG中,
,
∴△AHE≌△MFG(AAS).
∴FM=HA=1.
即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值1,
∴S△FCG=GC?FM=(3﹣x)×1=﹣x+(0≤x≤).
一、选择题(每小题3分,共12小题)
1.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.在下列函数中:①y=﹣8x;②;③;④y=﹣8x2+5;⑤y=﹣0.5x﹣1,一次函数有( )
A.1个 B.2个 C.3个 D.4个
3.在下列长度的四组线段中,不能组成直角三角形的是( )
A.a=5,b=12,c=13 B.,c=2
C.a:b:c=3:4:5 D.a=4,b=5,c=6
4.下列对于一次函数y=﹣3x+2的描述错误的是( )
A.y随x的增大而减小
B.图象经过点(2,4)
C.图象与直线y=3x相交
D.图象可由直线y=﹣3x向上平移2个单位得到
5.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量其中三个角是否都为直角
6.点A(﹣2,y1),B(3,y2)是一次函数y=﹣2x+1图象上的两点,则( )
A.y1>y2 B.y1≥y2 C.y1<y2 D.y1≤y2
7.如图,若在某棋盘上建立直角坐标系,使“将”位于点(2,﹣1),则“炮”位于点( )
A.(﹣1,2) B.(﹣1,3) C.(﹣2,3) D.(﹣2,2)
8.等腰Rt△ABO在平面直角坐标系中的位置如图所示,已知点A(﹣2,0),AB=BO,则点B的坐标为( )
A.(﹣1,1) B.(﹣1,2) C.(1,﹣1) D.(﹣1,﹣2)
9.如图反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为a千米,小刚在青稞地除草比在菜地浇水多用了b分钟,则a,b的值分别为( )
A.1,8 B.0.5,12 C.1,12 D.0.5,8
10.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AC=2,则S△ABE的值是( )
A.4 B.5 C.6 D.8
11.如图,E、F分别是?ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15,S△BQC=25,则阴影部分的面积为( )
A.40 B.45 C.50 D.55
12.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列四个结论:
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④S△ACD:S△ACB=1:3.
其中正确的有( )
A.只有①②③ B.只有①②④ C.只有①③④ D.①②③④
二、填空题(每小题3分,满分18分)
13.已知正n边形的一个内角为140°,则n等于 .
14.将一组有80个数据的样本分成6个组,第1~4组的频数分别是14,13,18,11,第5组的频率是0.2,则第6组的频数是 .
15.若一次函数y=kx﹣3(k为常数,k≠0)的图象经过第二、三、四象限,则k的值可以是 .(写出一个即可)
16.如图,CD是Rt△ABC的中线,∠ACB=90°,∠ABC=25°,则∠ADC的度数是 .
17.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是 cm2.
18.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…顶点依次用A1,A2,A3,A4…表示,则顶点A2021的坐标是 .
三、解答题(每小题6分,共12分)
19.如图,网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)请作出△ABC关于y轴的轴对称图形△A1B1C1,并写出△A1B1C1的顶点坐标;
(2)将△ABC先向下平移5个单位,再向左平移3个单位,得到△A2B2C2,写出△A2B2C2的顶点坐标,并作出该三角形.
20.如图,已知∠B=∠ADC=90°,DC=7,AB=20,BC=15,求AD的长.
四、解答题(每小题8分,共16分)
21.某班进行了一次数学考试,将成绩绘制成了不完整的频数分布直方图和频数分布表:
成绩 频数(人数) 频率
50≤x<60 4 0.08
60≤x<70 8 0.16
70≤x<80 20 0.4
80≤x<90 a 0.3
90≤x<100 3 b
(1)求频数分布表中a和b的值;
(2)将频数分布直方图补充完整;
(3)若成绩不低于80分为优秀,则该班本次数学考试的优秀率是多少?
22.某高铁修建过程中需要经过一座大山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D三点共线)处同时施工.测得∠CAB=30°,∠ABD=105°,AB=8km,求BD的长.(结果精确到0.1km,,)
五、应用题(每小题9分,共2小题,满分18分)
23.疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购2000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买A、B、C三种型号的口罩,其单价(元/袋)分别为30、35、40,若购买B型口罩的数量是A型的2倍,设购买A型口罩x袋,该企业购买口罩的总费用为y元.
(1)请求出y与x的函数关系式;
(2)已知口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,当购买A型口罩多少袋时购买口罩的总费用最少?并求最少总费用.
24.如图,在Rt△ABC中,∠ACB=90°,点E、F分别是AB、BC的中点,点D是CA延长线上的一点,且,连接DE、AF.
(1)求证:四边形ADEF是平行四边形;
(2)若四边形ADEF的周长是14cm,AC的长为4cm,求四边形ADEF的面积.
六、综合与探究(每小题10分,共2小题,满分20分)
25.如图,直线l1与l2相交于点P,点P横坐标为﹣4,l1的表达式为,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
(1)求点B的坐标和直线l2的表达式;
(2)若点M为直线l2上一点,且,求M的坐标.
26.如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,连接CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,请用含x的代数式表示△FCG的面积.
参考答案
一、选择题(每小题3分,共12小题,满分36分。每小题给出的四个选项中,只有一个选项是符合题目要求的,请把表示正确答案的字母填入下表中对应的题号下.)
1.下列图形中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
解:A.是轴对称图形,不是中心对称图形,故此选项不合题意;
B.既是轴对称图形,又是中心对称图形,故此选项符合题意;
C.是轴对称图形,不是中心对称图形,故此选项不合题意;
D.是轴对称图形,不是中心对称图形,故此选项不合题意;
故选:B.
2.在下列函数中:①y=﹣8x;②;③;④y=﹣8x2+5;⑤y=﹣0.5x﹣1,一次函数有( )
A.1个 B.2个 C.3个 D.4个
解:∵一次函数的解析式为y=kx+b(k≠0),
y=﹣8x,y=x+1,y=﹣0.5x﹣1符合一次函数解析式形式,
∴一次函数有①②⑤,
故选:C.
3.在下列长度的四组线段中,不能组成直角三角形的是( )
A.a=5,b=12,c=13 B.,c=2
C.a:b:c=3:4:5 D.a=4,b=5,c=6
解:A、52+122=132,能构成直角三角形,故本选项不符合题意;
B、()2+()2=22,能构成直角三角形,故本选项不符合题意;
C、(3x)2+(4x)2=(5x)2,能构成直角三角形,故本选项不符合题意;
D、52+42≠62,不能构成直角三角形,故本选项符合题意;
故选:D.
4.下列对于一次函数y=﹣3x+2的描述错误的是( )
A.y随x的增大而减小
B.图象经过点(2,4)
C.图象与直线y=3x相交
D.图象可由直线y=﹣3x向上平移2个单位得到
解:A、由于一次函数y=﹣3x+2中的k=﹣3<0,所以y随x的增大而减小,故不符合题意.
B、令x=2,则y=﹣6+2=﹣4,即一次函数y=﹣3x+2图象经过点(2,﹣4),故符合题意.
C、直线y=﹣3x+2中的k=﹣3,直线y=3x中的k=3,故两直线不平行,则相交,故不符合题意.
D、直线y=﹣3x向上平移2个单位得到y=﹣3x+2,故不符合题意.
故选:B.
5.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否相互平分
B.测量两组对边是否分别相等
C.测量对角线是否相等
D.测量其中三个角是否都为直角
解:A、对角线是否相互平分,能判定平行四边形;
B、两组对边是否分别相等,能判定平行四边形;
C、对角线相等的四边形不一定是矩形,不能判定形状;
D、其中四边形中三个角都为直角,能判定矩形.
故选:D.
6.点A(﹣2,y1),B(3,y2)是一次函数y=﹣2x+1图象上的两点,则( )
A.y1>y2 B.y1≥y2 C.y1<y2 D.y1≤y2
解:∵一次函数y=﹣2x+1的图象y随着x的增大而减小,
又∵﹣2<3
∴y1>y2,
故选:A.
7.如图,若在某棋盘上建立直角坐标系,使“将”位于点(2,﹣1),则“炮”位于点( )
A.(﹣1,2) B.(﹣1,3) C.(﹣2,3) D.(﹣2,2)
解:如图所示:“炮”位于点(﹣1,3).
故选:B.
8.等腰Rt△ABO在平面直角坐标系中的位置如图所示,已知点A(﹣2,0),AB=BO,则点B的坐标为( )
A.(﹣1,1) B.(﹣1,2) C.(1,﹣1) D.(﹣1,﹣2)
解:如图,过点B作BE⊥AO于E,
∵点A(﹣2,0),
∴AO=2,
∵AB=BO,∠ABO=90°,
∴AE=BE=EO=1,
∴点B(﹣1,1),
故选:A.
9.如图反映的过程是:小刚从家去菜地浇水,又去青稞地除草,然后回家,如果菜地和青稞地的距离为a千米,小刚在青稞地除草比在菜地浇水多用了b分钟,则a,b的值分别为( )
A.1,8 B.0.5,12 C.1,12 D.0.5,8
解:此函数大致可分以下几个阶段:
①0﹣12分种,小刚从家走到菜地;
②12﹣27分钟,小刚在菜地浇水;
③27﹣33分钟,小刚从菜地走到青稞地;
④33﹣56分钟,小刚在青稞地除草;
⑤56﹣74分钟,小刚从青稞地回到家;
综合上面的分析得:由③的过程知,a=1.5﹣1=0.5千米;
由②、④的过程知b=(56﹣33)﹣(27﹣12)=8分钟.
故选:D.
10.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,AC=2,则S△ABE的值是( )
A.4 B.5 C.6 D.8
解:∵DE垂直平分AB,
∴AE=BE,
∴∠EAB=∠B=15°,
∴∠AEC=∠B+∠BAE=30°,
∵∠ACE=90°,AC=2,
∴AE=BE=2AC=4,
∴S△ABE=BE?AC=,
故选:A.
11.如图,E、F分别是?ABCD的边AB、CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若S△APD=15,S△BQC=25,则阴影部分的面积为( )
A.40 B.45 C.50 D.55
解:如图,连接E、F两点,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=15,S△BQC=25,
∴S四边形EPFQ=S△APD+S△BQC=15+25=40,
故选:A.
12.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列四个结论:
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④S△ACD:S△ACB=1:3.
其中正确的有( )
A.只有①②③ B.只有①②④ C.只有①③④ D.①②③④
解:根据作图方法可得AD是∠BAC的平分线,故①正确;
∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=30°,
∴∠ADC=60°,故②正确;
∵∠B=30°,∠DAB=30°,
∴AD=DB,
∴点D在AB的中垂线上,故③正确;
∵∠CAD=30°,
∴CD=AD,
∵AD=DB,
∴CD=DB,
∴CD=CB,
S△ACD=CD?AC,S△ACB=CB?AC,
∴S△ACD:S△ACB=1:3,故④正确,
故选:D.
二、填空题(每小题3分,满分18分)
13.已知正n边形的一个内角为140°,则n等于 9 .
解:法一、由题意,得(n﹣2)×180=140n,
解得n=9.
故答案为:9.
法二、∵正n边形的一个内角为140°,其外角都为40°.
由于多边形的外角和为360°,
所以n为:360÷40=9.
故答案为:9.
14.将一组有80个数据的样本分成6个组,第1~4组的频数分别是14,13,18,11,第5组的频率是0.2,则第6组的频数是 8 .
解:∵第5组的频数为80×0.2=16,
∴第6组的频数为80﹣(14+13+18+11+16)=8,
故答案为:8.
15.若一次函数y=kx﹣3(k为常数,k≠0)的图象经过第二、三、四象限,则k的值可以是 ﹣1(答案不唯一) .(写出一个即可)
解:因为一次函数y=kx﹣3(k是常数,k≠0)的图象经过第二、三、四象限,
所以k<0,﹣3<0,
所以k可以取﹣1,
故答案为:﹣1(答案不唯一).
16.如图,CD是Rt△ABC的中线,∠ACB=90°,∠ABC=25°,则∠ADC的度数是 50° .
解:∵CD是Rt△ABC的中线,∠ACB=90°,
∴DC=DB,
∴∠DCB=∠ABC=25°,
∴∠ADC=∠DCB+∠ABC=50°,
故答案是:50°.
17.在菱形ABCD中,两条对角线相交于点O,且AB=10cm,AC=12cm.则菱形ABCD的面积是 96 cm2.
解:∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC=AC=6cm,OB=OD,
∴OB===8(cm),
∴BD=2OB=16cm,
∴S菱形ABCD=AC?BD=×12×16=96(cm2).
故答案为:96.
18.如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…顶点依次用A1,A2,A3,A4…表示,则顶点A2021的坐标是 (﹣506,﹣506) .
解:观察发现:A1(﹣1,﹣1),A2(﹣1,1),A3(1,1),A4(1,﹣1),A5(﹣2,﹣2),A6(﹣2,2),A7(2,2),A8(2,﹣2),A9(﹣3,﹣3),…,
∴A4n+1(﹣n﹣1,﹣n﹣1),A4n+2(﹣n﹣1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,﹣n﹣1)(n为自然数),
∵2021=505×4+1,
∴A2021(﹣506,﹣506).
故答案为:(﹣506,﹣506).
三、解答题(每小题6分,共12分)
19.如图,网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)请作出△ABC关于y轴的轴对称图形△A1B1C1,并写出△A1B1C1的顶点坐标;
(2)将△ABC先向下平移5个单位,再向左平移3个单位,得到△A2B2C2,写出△A2B2C2的顶点坐标,并作出该三角形.
解:(1)△A1B1C1如图所示:
A1 (﹣1,0),B1 (﹣5,2)C1,(﹣3,4);
(2)△A2B2C2如图所示:
A2 (﹣2,﹣5),B2 (2,﹣3),C2 (0,﹣1).
20.如图,已知∠B=∠ADC=90°,DC=7,AB=20,BC=15,求AD的长.
解:连接AC,在Rt△ABC中,AB=20,BC=15,
∴AC2=AB2+BC2=202+152=625,
在Rt△ADC中,DC=7,
∴AD=.
四、解答题(每小题8分,共16分)
21.某班进行了一次数学考试,将成绩绘制成了不完整的频数分布直方图和频数分布表:
成绩 频数(人数) 频率
50≤x<60 4 0.08
60≤x<70 8 0.16
70≤x<80 20 0.4
80≤x<90 a 0.3
90≤x<100 3 b
(1)求频数分布表中a和b的值;
(2)将频数分布直方图补充完整;
(3)若成绩不低于80分为优秀,则该班本次数学考试的优秀率是多少?
解:(1)某班的学生有:4÷0.08=50(人),
a=50×0.3=15,b=3÷50=0.06,
答:频数分布表中a和b的值分别为15,0.06;
(2)补全频数分布直方图如图所示;
(3)成绩不低于80分的频率为0.3+0.06=0.36,
∴该班本次数学考试的优秀率是0.36=36%,
答:该班本次数学考试的优秀率是36%.
22.某高铁修建过程中需要经过一座大山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D三点共线)处同时施工.测得∠CAB=30°,∠ABD=105°,AB=8km,求BD的长.(结果精确到0.1km,,)
解:如图,过点B作BE⊥AD于点E,
∵∠EAB=30°,AB=8km,
∴BE=,∠ABE=60°.
又∵∠ABD=105°,
∴∠DBE=∠ABD﹣∠ABE=45°.
∴Rt△BDE是等腰直角三角形.
∴BD=
=
=4
=5.656
≈5.7(km).
答:BD长约为5.7km.
五、应用题(每小题9分,共2小题,满分18分)
23.疫情期间,某企业为了保证能够尽快复工复产,准备为员工采购2000袋医用口罩.因为疫情期间口罩等物资紧缺,无法购买同型号的口罩,经市场调研,准备购买A、B、C三种型号的口罩,其单价(元/袋)分别为30、35、40,若购买B型口罩的数量是A型的2倍,设购买A型口罩x袋,该企业购买口罩的总费用为y元.
(1)请求出y与x的函数关系式;
(2)已知口罩生产厂家能提供的A型口罩的数量不大于C型口罩的数量,当购买A型口罩多少袋时购买口罩的总费用最少?并求最少总费用.
解:(1)根据题意得购买B型口罩为2x袋,购买C型口罩(2000﹣x﹣2x)袋,
∴y=30x+35×2x+40×(2000﹣x﹣2x)=80000﹣20x;
(2)依题意,得:x≤2000﹣x﹣2x,
解得:x≤500.
∵k=﹣20<0,
∴y随x的增大而减小,
当x=500时,y取得最小值,y最小=80000﹣20×500=70000(元).
答:当购买A型口罩500袋时,购买口罩的总费用最少,最少总费用为70000元.
24.如图,在Rt△ABC中,∠ACB=90°,点E、F分别是AB、BC的中点,点D是CA延长线上的一点,且,连接DE、AF.
(1)求证:四边形ADEF是平行四边形;
(2)若四边形ADEF的周长是14cm,AC的长为4cm,求四边形ADEF的面积.
【解答】(1)证明:∵点E、F分别是AB、BC的中点,
∴EF是△ABC的中位线,
∴EF=AC,EF∥AC,
∵AD=AC,
∴EF=AD,
∵EF∥AD,
∴四边形ADEF是平行四边形;
(2)解:∵四边形ADEF是平行四边形,四边形ADEF的周长是14cm,
∴AD=EF,AF=DE,AD+AF=7cm,
∵AC的长为4cm,
∴AD=AC=×4=2(cm),
∴AF=7﹣AD=7﹣2=5(cm),
在Rt△ACF中,由勾股定理得:CF===3(cm),
∴四边形ADEF的面积=AD?CF=2×3=6(cm2).
六、综合与探究(每小题10分,共2小题,满分20分)
25.如图,直线l1与l2相交于点P,点P横坐标为﹣4,l1的表达式为,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
(1)求点B的坐标和直线l2的表达式;
(2)若点M为直线l2上一点,且,求M的坐标.
解:(1)当x=0时,y=x+3=3,
则A(0,3),
而点A与点B恰好关于x轴对称,
所以B点坐标为(0,﹣3);
当x=﹣4时,y=x+3=1,
则P(﹣4,1),
设直线l2的表达式为y=kx+b,
把B(0,﹣3),P(﹣4,1)分别代入得,
解得,
所以直线l2的表达式为y=﹣x﹣3;
(2)设M点的横坐标为t,则它的纵坐标为﹣t﹣3,
因为:S△PAB=×[3﹣(﹣3)]×|﹣4|=12,
S△MAB=×[3﹣(﹣3)]×|t|=3|t|,
,
所以有:3|t|=×12,
解得:t=2或﹣2,
所以M点的坐标为(2,﹣5)或(﹣2,﹣1).
26.如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,连接CF.
(1)当DG=1时,求证:菱形EFGH为正方形;
(2)设DG=x,请用含x的代数式表示△FCG的面积.
【解答】证明:(1)∵四边形EFGH为菱形,
∴EH=HG,
在Rt△AHE和Rt△DGH中,
,
∴Rt△AHE≌Rt△DGH(HL),
∴∠AHE=∠DGH,
又∵∠DGH+∠DHG=90°,
∴∠AHE+∠DHG=90°,
则∠GHE=90°.
所以菱形EFGH为正方形;
(2)如图,过点F作FM⊥DC交DC所在直线于M,连接GE.
∵AB∥CD,
∴∠AEG=∠MGE,
∵HE∥GF,
∴∠HEG=∠FGE.
∴∠HEA=∠FGM,
在△AHE和△MFG中,
,
∴△AHE≌△MFG(AAS).
∴FM=HA=1.
即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值1,
∴S△FCG=GC?FM=(3﹣x)×1=﹣x+(0≤x≤).
同课章节目录
