2020-2021学年湖南省怀化市部分县区八年级(下)期末数学试卷 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年湖南省怀化市部分县区八年级(下)期末数学试卷 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 864.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 05:59:23 | ||
图片预览




文档简介
2020-2021学年湖南省怀化市部分县区八年级(下)期末数学试卷
一、选择题(每题4分,共40分).
2.如图,CD是△ABC的边AB上的中线,且CD=AB,则下列结论错误的是( )
A.AD=BD B.∠A=30°
C.∠ACB=90° D.△ADC与△BCD的面积相等
3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
4.下列图形中是中心对称图形的是( )
A. B. C. D.
5.如图,在?ABCD中,AB=6cm,BC=10cm,AC=8cm,BD=14cm,则下列结论中:①△AOB的周长是17cm,②△ACD是直角三角形,③AD=14cm,④?ABCD的面积是48cm2,其中正确有( )
A.1个 B.2个 C.3个 D.4个
6.如点A(﹣a,a﹣2)在第二象限,那么a的值可能是( )
A.0 B.1 C.2 D.3
7.若点A(2,4)在函数y=kx﹣2的图象上,则下列各点在函数图象上的是( )
A.(0,﹣2) B.(,0) C.(8,20) D.(,)
8.如图,四边形ABCD的对角线AC、BD相交于O,下列判断正确的是( )
A.若AC⊥BD,则四边形ABCD是菱形
B.若AC=BD,则四边形ABCD是矩形
C.若AB=DC,AD∥BC,则四边形ABCD是平行四边形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
9.在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
10.已知直线y=2x﹣4,则它与两坐标轴围成的三角形的面积是( )
A.2 B.3 C.4 D.5
二、填空题(每小题4分,共24分)
11.已知点A(﹣3,a)与点B(﹣3,﹣4)关于x轴对称,则a= .
12.函数y=﹣x+1的图象不经过第 象限.
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是 .
14.某同学做掷硬币试验,正面朝上记为“正”,反面朝上记为“反”,结果统计如下:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 反 正 正 反 正 正 反
则“正面朝上”的频数是 ;“反面朝上”的频率是 .
15.如图,一次函数y=kx+b的图象与坐标轴的交点坐标分别为A(0,2),B(﹣3,0),下列说法:①y随x的增大而减小;②b=﹣3;③关于x的方程kx+b=0的解为x=2;④关于x的不等式kx+b<0的解集x<﹣3.其中说法正确的有 .
16.如图,某校的生物园形状是一个直角三角形,∠ACB=90°,AC=40m,BC=30m.现要修建一条水渠CD,D点在边AB上,若水渠的造价为800元/m,则修建水渠CD最少要 元.
三、解答题(本大题共86分)
17.已知正比例函数的图象经过点M(﹣1,5).
(1)求这个函数的表达式;
(2)若将这个函数的图象向上平移5个单位后,写出图象与y轴的交点坐标.
18.如图,四边形ABCD中,AB=CD,∠ABC=90°,∠ADC=90°.求证:AD=BC.
19.如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆(B)位置的坐标;
(2)若体育馆位置坐标为C(﹣3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
20.如图,在?ABCD中,E在BC的延长线上,且CE=BC,AE与CD相交于F.
(1)求证:AC=DE;
(2)若∠BAE=90°,线段AE与CD是什么关系?为什么?
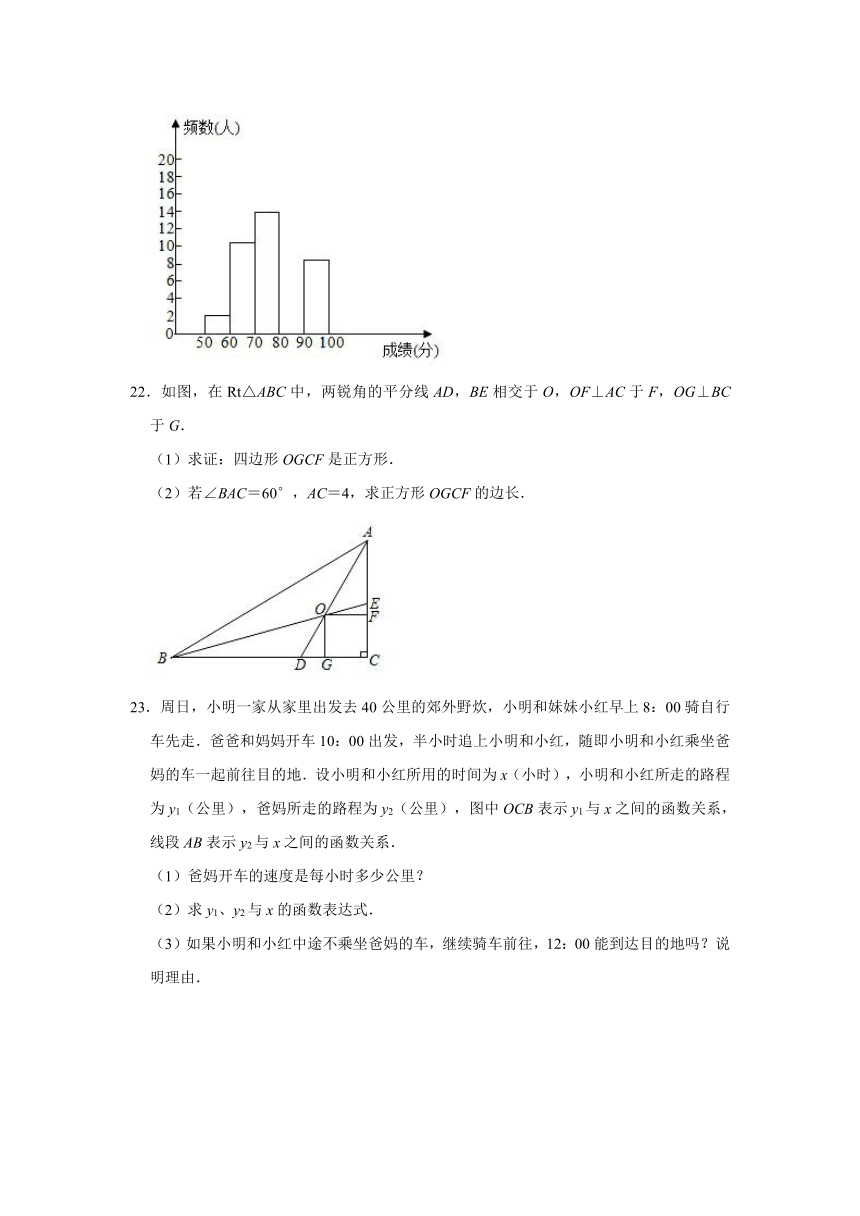
21.为了提高学生书写汉字的能力,增强保护汉字的意识,育才学校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,决赛规则是:同时听写100个汉字,每正确听写出一个汉字得1分.若用x(分)表示学生成绩,结果50≤x≤100,将其按分数段分为五组,绘制出不完整表格及直方图.
组别 成绩x(分) 频数(人数) 频率
一 50≤x<60 2 0.04
二 60≤x<70 10 0.2
三 70≤x<80 14 b
四 80≤x<90 a 0.32
五 90≤x<100 8 0.16
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 名学生参加;
(2)求a,b的值,并补全右边的直方图;
(3)若决赛成绩不低于80分为优秀,求本次大赛的优秀率.
22.如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
23.周日,小明一家从家里出发去40公里的郊外野炊,小明和妹妹小红早上8:00骑自行车先走.爸爸和妈妈开车10:00出发,半小时追上小明和小红,随即小明和小红乘坐爸妈的车一起前往目的地.设小明和小红所用的时间为x(小时),小明和小红所走的路程为y1(公里),爸妈所走的路程为y2(公里),图中OCB表示y1与x之间的函数关系,线段AB表示y2与x之间的函数关系.
(1)爸妈开车的速度是每小时多少公里?
(2)求y1、y2与x的函数表达式.
(3)如果小明和小红中途不乘坐爸妈的车,继续骑车前往,12:00能到达目的地吗?说明理由.
24.如图,直线与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为x轴上一动点.
(1)填空:A点坐标是 ,B点的坐标是 .
(2)当P是OA的中点时,四边形PCDO是 形,其周长是 .
(3)当PC+PD最小时,求P点的坐标.
(4)是否存在P点,使△PCD是等腰三角形?若存在,请求出P点的坐标.
参考答案
一、选择题(每小题4分,共40分)
2.如图,CD是△ABC的边AB上的中线,且CD=AB,则下列结论错误的是( )
A.AD=BD B.∠A=30°
C.∠ACB=90° D.△ADC与△BCD的面积相等
【分析】根据CD是△ABC的边AB上的中线,且CD=AB,可以得到AD、BD和CD的关系,从而可以判断A是否正确,再根据等腰三角形的性质和三角形内角和,可以得到∠ACB的度数,从而可以得到∠ACB的度数,即可判断C是否正确,最后根据三角形面积的求法,可以判断D是否正确;对于∠A,由题目中的条件,无法判断角的度数,从而可以判断B是否正确.
解:∵CD是△ABC的边AB上的中线,且CD=AB,
∴AD=BD=CD,故选项A正确,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
即∠ACB=90°,故选项C正确;
∵AD=BD,
∴△ADC与△BCD是等底同高的两个三角形,
∴△ADC与△BCD的面积相等,故选项D正确;
无法判断∠A的度数,故选项B错误;
故选:B.
3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
【分析】首先设此多边形为n边形,根据题意得:180(n﹣2)=540,即可求得n=5,再由多边形的外角和等于360°,即可求得答案.
解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5,
∴这个正多边形的每一个外角等于:=72°.
故选:C.
4.下列图形中是中心对称图形的是( )
A. B. C. D.
【分析】一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.根据中心对称图形的概念对各选项分析判断即可得解.
解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.是中心对称图形,故本选项符合题意;
D.不是中心对称图形,故本选项不符合题意.
故选:C.
5.如图,在?ABCD中,AB=6cm,BC=10cm,AC=8cm,BD=14cm,则下列结论中:①△AOB的周长是17cm,②△ACD是直角三角形,③AD=14cm,④?ABCD的面积是48cm2,其中正确有( )
A.1个 B.2个 C.3个 D.4个
【分析】①根据平行四边形的对角线互相平分及对角线的长度求得AO和BO的长即可求得△AOB的周长;
②根据勾股定理的逆定理求得∠BAC=90°,然后利用平行四边形的性质得到∠ADC=90°即可判断正误;
③根据平行四边形的对边相等得到AD=BC=10cm;
④直接利用底乘高求得面积即可.
解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AC=8cm,BD=14cm,
∴AO=4cm,BO=7cm,
∵AB=6cm,
∴△AOB的周长=AB+AO+BO=6+4+7=17cm,
故①正确;
∵AB=6cm,BC=10cm,AC=8cm,
∴AB2+AC2=62+82=102=BC2,
∴∠BAC=90°,
∵AB∥CD,
∴∠DCA=∠BAC=90°,
∴△ACD是直角三角形,
故②正确;
∵四边形ABCD是平行四边形,
∴AD=BC=10cm,
故③错误;
?ABCD的面积=AB?AC=6×8=48cm2,
故④正确,
正确的有3个,
故选:C.
6.如点A(﹣a,a﹣2)在第二象限,那么a的值可能是( )
A.0 B.1 C.2 D.3
【分析】根据点在第二象限得出不等式组,再求出不等式组的解集,最后逐个判断即可.
解:∵点A(﹣a,a﹣2)在第二象限,
∴,
解得:a>2,
A.0<2,故本选项不符合题意;
B.1<2,故本选项不符合题意;
C.2=2,故本选项不符合题意;
D.3>2,故本选项符合题意;
故选:D.
7.若点A(2,4)在函数y=kx﹣2的图象上,则下列各点在函数图象上的是( )
A.(0,﹣2) B.(,0) C.(8,20) D.(,)
【分析】将点A(2,4)代入函数解析式求k,再把点的坐标代入解析式,逐一检验.
解:把点A(2,4)代入y=kx﹣2中,
得2k﹣2=4,解得k=3;
所以,y=3x﹣2,
四个选项中,只有A符合y=3×0﹣2=﹣2.
故选:A.
8.如图,四边形ABCD的对角线AC、BD相交于O,下列判断正确的是( )
A.若AC⊥BD,则四边形ABCD是菱形
B.若AC=BD,则四边形ABCD是矩形
C.若AB=DC,AD∥BC,则四边形ABCD是平行四边形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
【分析】由矩形的判定、菱形的判定?以及平行四边形的判定分别对各个选项进行判断即可.
解:A、若AC⊥BD,则四边形ABCD不一定是菱形,故选项A不符合题意;
B、若AC=BD,则四边形不一定ABCD是矩形,故选项B不符合题意;
C、若AB=DC,AD∥BC,则四边形ABCD不一定是平行四边形,故选项C不符合题意;
D、∵AO=OC,BO=OD,∴四边形ABCD是平行四边形,故选项D符合题意;
故选:D.
9.在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
【分析】因为D点坐标为(2,3),由平行四边形的性质,可知C点的纵坐标一定是3,又由D点相对于A点横坐标移动了2,故可得C点横坐标为2+5=7,即顶点C的坐标(7,3).
解:已知A,B,D三点的坐标分别是(0,0),(5,0),(2,3),
∵AB在x轴上,
∴点C与点D的纵坐标相等,都为3,
又∵D点相对于A点横坐标移动了2﹣0=2,
∴C点横坐标为2+5=7,
∴即顶点C的坐标(7,3).
故选:C.
10.已知直线y=2x﹣4,则它与两坐标轴围成的三角形的面积是( )
A.2 B.3 C.4 D.5
【分析】先根据坐标轴的坐标特征分别求出直线y=2x﹣4与两坐标轴的交点坐标,然后根据三角形的面积公式计算.
解:令y=0,则2x﹣4=0,解得x=2,所以直线y=2x﹣4与x轴的交点坐标为(2,0);
令x=0,则y=2x﹣4=0,所以直线y=2x﹣4与y轴的交点坐标为(0,﹣4),
所以此直线与两坐标轴围成的三角形面积=×2×|﹣4|=4.
故选:C.
二、填空题(每小题4分,共24分)
11.已知点A(﹣3,a)与点B(﹣3,﹣4)关于x轴对称,则a= 4 .
【分析】关于x轴的对称点的坐标特点:横坐标相同,纵坐标互为相反数.据此可得a的值.
解:∵点A(﹣3,a)与点B(﹣3,﹣4)关于x轴对称,
∴a与﹣4互为相反数,
∴a=4,
故答案为:4.
12.函数y=﹣x+1的图象不经过第 三 象限.
【分析】先根据一次函数y=﹣x+1中k=﹣,b=1判断出函数图象经过的象限,进而可得出结论.
解:∵一次函数y=﹣x+1中k=﹣<0,b=1>0,
∴此函数的图象经过一、二、四象限,不经过第三象限.
故答案为:三.
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是 16 .
【分析】先利用三角形中位线性质得到AB=4,然后根据菱形的性质计算菱形ABCD的周长.
解:∵E,F分别是AD,BD的中点,
∴EF为△ABD的中位线,
∴AB=2EF=4,
∵四边形ABCD为菱形,
∴AB=BC=CD=DA=4,
∴菱形ABCD的周长=4×4=16.
故答案为16.
14.某同学做掷硬币试验,正面朝上记为“正”,反面朝上记为“反”,结果统计如下:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 反 正 正 反 正 正 反
则“正面朝上”的频数是 6 ;“反面朝上”的频率是 0.4 .
【分析】根据实验结果得出结论即可.
解:某同学做掷硬币试验,共抛了10次,6次正面朝上,4次反面朝上,则正面朝上的频数是6,反面朝上的频数是4,“反面朝上”的频率是:=0.4.
故答案是:6;0.4.
15.如图,一次函数y=kx+b的图象与坐标轴的交点坐标分别为A(0,2),B(﹣3,0),下列说法:①y随x的增大而减小;②b=﹣3;③关于x的方程kx+b=0的解为x=2;④关于x的不等式kx+b<0的解集x<﹣3.其中说法正确的有 ④ .
【分析】根据一次函数的性质,一次函数与一元一次方程的关系对各个说法分析判断即可得解.
解:①如图所示:y随x的增大而增大,故说法错误;
②由于一次函数y=kx+b的图象与y轴交点是(0,2),所以b=2,故说法错误;
③由于一次函数y=kx+b的图象与x轴的交点坐标是(﹣3,0),所以关于x的方程kx+b=0的解为x=﹣3,故说法错误;
④如图所示:关于x的不等式kx+b<0的解集x<﹣3,故说法正确.
综上所述,说法正确的结论是:④.
故答案是:④.
16.如图,某校的生物园形状是一个直角三角形,∠ACB=90°,AC=40m,BC=30m.现要修建一条水渠CD,D点在边AB上,若水渠的造价为800元/m,则修建水渠CD最少要 38400 元.
【分析】要使水渠造价最低,则CD最短,利用勾股定理求出AB的长度,利用等面积法求出CD即可.
解:当CD为斜边上的高时,CD最短,从而水渠造价最低,
∵∠ACB=90°,AC=40m,BC=30m,
∴AB===50m,
∵CD?AB=AC?BC,
即CD?100=80×60,
∴CD=48m,
此时,最低造价为38400元,
所以,CD长为48米,水渠的造价最低,其最低造价为38400元,
故答案为:38400.
三、解答题(本大题共86分)
17.已知正比例函数的图象经过点M(﹣1,5).
(1)求这个函数的表达式;
(2)若将这个函数的图象向上平移5个单位后,写出图象与y轴的交点坐标.
【分析】(1)利用待定系数法确定函数关系式;
(2)根据“上加下减”平移规律写出新直线方程,利用直线方程求得该图象与y轴的交点坐标.
解:(1)设函数表达式为y=kx,
因为它的图象经过点M(﹣1,5),则5=﹣k,
解得k=﹣5.
故所求的表达式为y=﹣5x.
(2)将函数y=﹣5x的图象向上平移5个单位后所得函数街系数为为y=﹣5x+5.
令x=0,则y=5.
所以该函数图象与y轴的交点坐标是(0,5).
18.如图,四边形ABCD中,AB=CD,∠ABC=90°,∠ADC=90°.求证:AD=BC.
【分析】根据直角三角形的定义得到△ABC和△CDA是直角三角形,根据全等三角形的判定和性质定理即可得到结论.
【解答】证明:∵∠ABC=90°,∠ADC=90°.
∴△ABC和△CDA是直角三角形,
在Rt△ABC和Rt△CDA中,
,
∴Rt△ABC≌Rt△CDA(HL),
∴AD=CB.
19.如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆(B)位置的坐标;
(2)若体育馆位置坐标为C(﹣3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
【分析】(1)利用点A的坐标画出直角坐标系;根据点的坐标的意义描出点B;
(2)利用三角形的面积得到△ABC的面积.
解:(1)建立直角坐标系如图所示:
图书馆(B)位置的坐标为(﹣3,﹣2);
(2)标出体育馆位置C如图所示,观察可得,△ABC中BC边长为5,BC边上的高为4,所以△ABC的面积为==10.
20.如图,在?ABCD中,E在BC的延长线上,且CE=BC,AE与CD相交于F.
(1)求证:AC=DE;
(2)若∠BAE=90°,线段AE与CD是什么关系?为什么?
【分析】(1)理由平行四边形的性质证得四边形ACED是平行四边形即可证得结论;
(2)判定四边形ACED是菱形后即可证得对角线互相垂直平分.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=CE AD∥BE,
又CE=BC,
∴AD=CE,
∴四边形ACED是平行四边形,
∴AC=DE;
(2)解:互相垂直平分;
理由:∵∠BAE=90°,BC=CE,
∴AC=CE,
∴四边形ACED是菱形,
∴AE与CD互相垂直平分.
21.为了提高学生书写汉字的能力,增强保护汉字的意识,育才学校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,决赛规则是:同时听写100个汉字,每正确听写出一个汉字得1分.若用x(分)表示学生成绩,结果50≤x≤100,将其按分数段分为五组,绘制出不完整表格及直方图.
组别 成绩x(分) 频数(人数) 频率
一 50≤x<60 2 0.04
二 60≤x<70 10 0.2
三 70≤x<80 14 b
四 80≤x<90 a 0.32
五 90≤x<100 8 0.16
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 50 名学生参加;
(2)求a,b的值,并补全右边的直方图;
(3)若决赛成绩不低于80分为优秀,求本次大赛的优秀率.
【分析】(1)根据表格中的数据可以求得本次决赛的学生数;
(2)根据(1)中决赛学生数,可以求得a、b的值;根据a的值,可以将频数分布直方图补充完整;
(3)根据表格中的数据可以求得本次大赛的优秀率.
解:(1)由表格可得,
本次决赛的学生数为:10÷0.2=50(名),
故答案为:50;
(2)a=50×0.32=16,b=14÷50=0.28,
补全的频数分布直方图如图所示,
(3)由表格可得,
决赛成绩不低于80分为优秀率为:(0.32+0.16)×100%=48%,
答:本次大赛的优秀率为48%.
22.如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
【分析】(1)根据有三个角是直角的四边形是矩形,可得四边形OGCF是矩形,根据角平分线的性质,可得OH与OF,OH与OG的关系,根据邻边相等的矩形是正方形,可得答案;
(2)由含30°角的直角三角形的性质和勾股定理求出AB和BC,根据全等三角形判定的HL定理证得Rt△AOH≌Rt△AOF得到AH=AF,设正方形OGCF的边长为x,则AH=AF=4﹣x,BH=BG=4﹣x,根据AB=AH+BH=8,解方程即可求出x.
【解答】(1)证明:过O作OH⊥AB于H点,
∵OF⊥AC于点F,OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD,BE分别是∠BAC,∠ABC的角平分线,OF⊥AC,OG⊥BC,
∴OG=OH=OF,
又四边形OGCF是矩形,
∴四边形OGCF是正方形;
(2)解:在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=90°﹣∠BAC=90°﹣60°=30°,
∴AC=AB,
∵AC=4,
∴AB=2AC=2×4=8,
∵AC2+BC2=AB2,
∴BC==4,
在Rt△AOH和Rt△AOF中,
,
∴Rt△AOH≌Rt△AOF(HL),
∴AH=AF,
设正方形OGCF的边长为x,
则AH=AF=4﹣x,BH=BG=4﹣x,
∴4﹣x+4﹣x=8,
∴x=2﹣2,
即正方形OGCF的边长为2﹣2.
23.周日,小明一家从家里出发去40公里的郊外野炊,小明和妹妹小红早上8:00骑自行车先走.爸爸和妈妈开车10:00出发,半小时追上小明和小红,随即小明和小红乘坐爸妈的车一起前往目的地.设小明和小红所用的时间为x(小时),小明和小红所走的路程为y1(公里),爸妈所走的路程为y2(公里),图中OCB表示y1与x之间的函数关系,线段AB表示y2与x之间的函数关系.
(1)爸妈开车的速度是每小时多少公里?
(2)求y1、y2与x的函数表达式.
(3)如果小明和小红中途不乘坐爸妈的车,继续骑车前往,12:00能到达目的地吗?说明理由.
【分析】(1)根据题意和函数图象可以求得爸妈开车的速度;
(2)利用待定系数法求出y2与x的函数表达式,根据题意可以求得点C的坐标,再用待定系数法分段求出y1与x之间的函数关系式,并写出自变量的取值范围;
(3)根据OC段的解析式可以求得小明和小红中途不乘坐爸妈的车,继续骑车前往所用时间,即可得出结论.
解:(1)由函数图象得:爸爸和妈妈开车到达目的地的时间为3﹣2=1(小时),
∴爸妈开车的速度是:40÷1=40(公里/小时),
答:爸妈开车的速度是每小时40公里;
(2)设y2=kx+b,从图中知其图象经过(2,0)和(3,40),
则,
解得 ,
∴y2=40x﹣80(2≤x≤3);
当x=2.5时,y2=20,所以C点为(2.5,20),
又设OC的解析式为y1=mx,
则2.5m=20,解得m=8,
则y1=8x(0≤x≤2.5),
CB段的解析式是y2相同,
所以 ;
(3)在直线OC上,当y=40时,x=5,这说明小明他们不乘坐爸妈的车,全程需要5个小时,即13:00才能到达,所以他们12:00不能到达.
24.如图,直线与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为x轴上一动点.
(1)填空:A点坐标是 (﹣8,0) ,B点的坐标是 (0,6) .
(2)当P是OA的中点时,四边形PCDO是 矩 形,其周长是 24 .
(3)当PC+PD最小时,求P点的坐标.
(4)是否存在P点,使△PCD是等腰三角形?若存在,请求出P点的坐标.
【分析】(1)对于,令=0,解得x=﹣8,令x=0,则y=6,即可求解;
(2)C、D的纵坐标相同,故CD∥OP,点C、P的横坐标相同,故CP∥OD,进而求解;
(3)作点C关于x轴的对称点C′(﹣4,﹣3),连接C′D交x轴于点P,则点P为所求点,进而求解;
(4)分PC=PD、PC=CD、PD=CD三种情况,分别求解即可.
解:(1)对于,令=0,解得x=﹣8,令x=0,则y=6,
故点A、B的坐标分别为(﹣8,0)、(0,6),
故答案为:(﹣8,0)、(0,6);
(2)∵C、D分别为线段AB、OB的中点,故点C、D的坐标分别为(﹣4,3)、(0,3),
∵P是OA的中点,故点P的坐标为(0,﹣4),
∵C、D的纵坐标相同,故CD∥OP,
点C、P的横坐标相同,故CP∥OD,
则四边形PCDO是平行四边形,而∠DOP=90°,
故四边形PCDO是矩形,
则四边形PCDO的周长=2(CD+CP)=2×(4+3)=24,
故答案为:矩,24;
(3)作点C关于x轴的对称点C′(﹣4,﹣3),连接C′D交x轴于点P,则点P为所求点,
设直线C′D的表达式为y=kx+b,
则,解得,
故直线C′D的表达式为y=x+3,
令y=x+3=0,解得x=﹣2,
故点P的坐标为(﹣2,0);
(4)设点P(x,0),
由点P、C、D的坐标得:PC2=(x+4)2+9,PD2=x2+9,CD2=16,
当PC=PD时,即(x+4)2+9=x2+9,解得x=﹣2,
当PC=CD时,则(x+4)2+9=16,解得x=﹣4±,
当PD=CD时,则x2+9=16,解得x=,
综上,点P的坐标为:(﹣2,0)(,0)(,0)(,0).
一、选择题(每题4分,共40分).
2.如图,CD是△ABC的边AB上的中线,且CD=AB,则下列结论错误的是( )
A.AD=BD B.∠A=30°
C.∠ACB=90° D.△ADC与△BCD的面积相等
3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
4.下列图形中是中心对称图形的是( )
A. B. C. D.
5.如图,在?ABCD中,AB=6cm,BC=10cm,AC=8cm,BD=14cm,则下列结论中:①△AOB的周长是17cm,②△ACD是直角三角形,③AD=14cm,④?ABCD的面积是48cm2,其中正确有( )
A.1个 B.2个 C.3个 D.4个
6.如点A(﹣a,a﹣2)在第二象限,那么a的值可能是( )
A.0 B.1 C.2 D.3
7.若点A(2,4)在函数y=kx﹣2的图象上,则下列各点在函数图象上的是( )
A.(0,﹣2) B.(,0) C.(8,20) D.(,)
8.如图,四边形ABCD的对角线AC、BD相交于O,下列判断正确的是( )
A.若AC⊥BD,则四边形ABCD是菱形
B.若AC=BD,则四边形ABCD是矩形
C.若AB=DC,AD∥BC,则四边形ABCD是平行四边形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
9.在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
10.已知直线y=2x﹣4,则它与两坐标轴围成的三角形的面积是( )
A.2 B.3 C.4 D.5
二、填空题(每小题4分,共24分)
11.已知点A(﹣3,a)与点B(﹣3,﹣4)关于x轴对称,则a= .
12.函数y=﹣x+1的图象不经过第 象限.
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是 .
14.某同学做掷硬币试验,正面朝上记为“正”,反面朝上记为“反”,结果统计如下:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 反 正 正 反 正 正 反
则“正面朝上”的频数是 ;“反面朝上”的频率是 .
15.如图,一次函数y=kx+b的图象与坐标轴的交点坐标分别为A(0,2),B(﹣3,0),下列说法:①y随x的增大而减小;②b=﹣3;③关于x的方程kx+b=0的解为x=2;④关于x的不等式kx+b<0的解集x<﹣3.其中说法正确的有 .
16.如图,某校的生物园形状是一个直角三角形,∠ACB=90°,AC=40m,BC=30m.现要修建一条水渠CD,D点在边AB上,若水渠的造价为800元/m,则修建水渠CD最少要 元.
三、解答题(本大题共86分)
17.已知正比例函数的图象经过点M(﹣1,5).
(1)求这个函数的表达式;
(2)若将这个函数的图象向上平移5个单位后,写出图象与y轴的交点坐标.
18.如图,四边形ABCD中,AB=CD,∠ABC=90°,∠ADC=90°.求证:AD=BC.
19.如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆(B)位置的坐标;
(2)若体育馆位置坐标为C(﹣3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
20.如图,在?ABCD中,E在BC的延长线上,且CE=BC,AE与CD相交于F.
(1)求证:AC=DE;
(2)若∠BAE=90°,线段AE与CD是什么关系?为什么?
21.为了提高学生书写汉字的能力,增强保护汉字的意识,育才学校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,决赛规则是:同时听写100个汉字,每正确听写出一个汉字得1分.若用x(分)表示学生成绩,结果50≤x≤100,将其按分数段分为五组,绘制出不完整表格及直方图.
组别 成绩x(分) 频数(人数) 频率
一 50≤x<60 2 0.04
二 60≤x<70 10 0.2
三 70≤x<80 14 b
四 80≤x<90 a 0.32
五 90≤x<100 8 0.16
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 名学生参加;
(2)求a,b的值,并补全右边的直方图;
(3)若决赛成绩不低于80分为优秀,求本次大赛的优秀率.
22.如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
23.周日,小明一家从家里出发去40公里的郊外野炊,小明和妹妹小红早上8:00骑自行车先走.爸爸和妈妈开车10:00出发,半小时追上小明和小红,随即小明和小红乘坐爸妈的车一起前往目的地.设小明和小红所用的时间为x(小时),小明和小红所走的路程为y1(公里),爸妈所走的路程为y2(公里),图中OCB表示y1与x之间的函数关系,线段AB表示y2与x之间的函数关系.
(1)爸妈开车的速度是每小时多少公里?
(2)求y1、y2与x的函数表达式.
(3)如果小明和小红中途不乘坐爸妈的车,继续骑车前往,12:00能到达目的地吗?说明理由.
24.如图,直线与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为x轴上一动点.
(1)填空:A点坐标是 ,B点的坐标是 .
(2)当P是OA的中点时,四边形PCDO是 形,其周长是 .
(3)当PC+PD最小时,求P点的坐标.
(4)是否存在P点,使△PCD是等腰三角形?若存在,请求出P点的坐标.
参考答案
一、选择题(每小题4分,共40分)
2.如图,CD是△ABC的边AB上的中线,且CD=AB,则下列结论错误的是( )
A.AD=BD B.∠A=30°
C.∠ACB=90° D.△ADC与△BCD的面积相等
【分析】根据CD是△ABC的边AB上的中线,且CD=AB,可以得到AD、BD和CD的关系,从而可以判断A是否正确,再根据等腰三角形的性质和三角形内角和,可以得到∠ACB的度数,从而可以得到∠ACB的度数,即可判断C是否正确,最后根据三角形面积的求法,可以判断D是否正确;对于∠A,由题目中的条件,无法判断角的度数,从而可以判断B是否正确.
解:∵CD是△ABC的边AB上的中线,且CD=AB,
∴AD=BD=CD,故选项A正确,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
即∠ACB=90°,故选项C正确;
∵AD=BD,
∴△ADC与△BCD是等底同高的两个三角形,
∴△ADC与△BCD的面积相等,故选项D正确;
无法判断∠A的度数,故选项B错误;
故选:B.
3.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )
A.108° B.90° C.72° D.60°
【分析】首先设此多边形为n边形,根据题意得:180(n﹣2)=540,即可求得n=5,再由多边形的外角和等于360°,即可求得答案.
解:设此多边形为n边形,
根据题意得:180(n﹣2)=540,
解得:n=5,
∴这个正多边形的每一个外角等于:=72°.
故选:C.
4.下列图形中是中心对称图形的是( )
A. B. C. D.
【分析】一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.根据中心对称图形的概念对各选项分析判断即可得解.
解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.是中心对称图形,故本选项符合题意;
D.不是中心对称图形,故本选项不符合题意.
故选:C.
5.如图,在?ABCD中,AB=6cm,BC=10cm,AC=8cm,BD=14cm,则下列结论中:①△AOB的周长是17cm,②△ACD是直角三角形,③AD=14cm,④?ABCD的面积是48cm2,其中正确有( )
A.1个 B.2个 C.3个 D.4个
【分析】①根据平行四边形的对角线互相平分及对角线的长度求得AO和BO的长即可求得△AOB的周长;
②根据勾股定理的逆定理求得∠BAC=90°,然后利用平行四边形的性质得到∠ADC=90°即可判断正误;
③根据平行四边形的对边相等得到AD=BC=10cm;
④直接利用底乘高求得面积即可.
解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AC=8cm,BD=14cm,
∴AO=4cm,BO=7cm,
∵AB=6cm,
∴△AOB的周长=AB+AO+BO=6+4+7=17cm,
故①正确;
∵AB=6cm,BC=10cm,AC=8cm,
∴AB2+AC2=62+82=102=BC2,
∴∠BAC=90°,
∵AB∥CD,
∴∠DCA=∠BAC=90°,
∴△ACD是直角三角形,
故②正确;
∵四边形ABCD是平行四边形,
∴AD=BC=10cm,
故③错误;
?ABCD的面积=AB?AC=6×8=48cm2,
故④正确,
正确的有3个,
故选:C.
6.如点A(﹣a,a﹣2)在第二象限,那么a的值可能是( )
A.0 B.1 C.2 D.3
【分析】根据点在第二象限得出不等式组,再求出不等式组的解集,最后逐个判断即可.
解:∵点A(﹣a,a﹣2)在第二象限,
∴,
解得:a>2,
A.0<2,故本选项不符合题意;
B.1<2,故本选项不符合题意;
C.2=2,故本选项不符合题意;
D.3>2,故本选项符合题意;
故选:D.
7.若点A(2,4)在函数y=kx﹣2的图象上,则下列各点在函数图象上的是( )
A.(0,﹣2) B.(,0) C.(8,20) D.(,)
【分析】将点A(2,4)代入函数解析式求k,再把点的坐标代入解析式,逐一检验.
解:把点A(2,4)代入y=kx﹣2中,
得2k﹣2=4,解得k=3;
所以,y=3x﹣2,
四个选项中,只有A符合y=3×0﹣2=﹣2.
故选:A.
8.如图,四边形ABCD的对角线AC、BD相交于O,下列判断正确的是( )
A.若AC⊥BD,则四边形ABCD是菱形
B.若AC=BD,则四边形ABCD是矩形
C.若AB=DC,AD∥BC,则四边形ABCD是平行四边形
D.若AO=OC,BO=OD,则四边形ABCD是平行四边形
【分析】由矩形的判定、菱形的判定?以及平行四边形的判定分别对各个选项进行判断即可.
解:A、若AC⊥BD,则四边形ABCD不一定是菱形,故选项A不符合题意;
B、若AC=BD,则四边形不一定ABCD是矩形,故选项B不符合题意;
C、若AB=DC,AD∥BC,则四边形ABCD不一定是平行四边形,故选项C不符合题意;
D、∵AO=OC,BO=OD,∴四边形ABCD是平行四边形,故选项D符合题意;
故选:D.
9.在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
【分析】因为D点坐标为(2,3),由平行四边形的性质,可知C点的纵坐标一定是3,又由D点相对于A点横坐标移动了2,故可得C点横坐标为2+5=7,即顶点C的坐标(7,3).
解:已知A,B,D三点的坐标分别是(0,0),(5,0),(2,3),
∵AB在x轴上,
∴点C与点D的纵坐标相等,都为3,
又∵D点相对于A点横坐标移动了2﹣0=2,
∴C点横坐标为2+5=7,
∴即顶点C的坐标(7,3).
故选:C.
10.已知直线y=2x﹣4,则它与两坐标轴围成的三角形的面积是( )
A.2 B.3 C.4 D.5
【分析】先根据坐标轴的坐标特征分别求出直线y=2x﹣4与两坐标轴的交点坐标,然后根据三角形的面积公式计算.
解:令y=0,则2x﹣4=0,解得x=2,所以直线y=2x﹣4与x轴的交点坐标为(2,0);
令x=0,则y=2x﹣4=0,所以直线y=2x﹣4与y轴的交点坐标为(0,﹣4),
所以此直线与两坐标轴围成的三角形面积=×2×|﹣4|=4.
故选:C.
二、填空题(每小题4分,共24分)
11.已知点A(﹣3,a)与点B(﹣3,﹣4)关于x轴对称,则a= 4 .
【分析】关于x轴的对称点的坐标特点:横坐标相同,纵坐标互为相反数.据此可得a的值.
解:∵点A(﹣3,a)与点B(﹣3,﹣4)关于x轴对称,
∴a与﹣4互为相反数,
∴a=4,
故答案为:4.
12.函数y=﹣x+1的图象不经过第 三 象限.
【分析】先根据一次函数y=﹣x+1中k=﹣,b=1判断出函数图象经过的象限,进而可得出结论.
解:∵一次函数y=﹣x+1中k=﹣<0,b=1>0,
∴此函数的图象经过一、二、四象限,不经过第三象限.
故答案为:三.
13.如图,在菱形ABCD中,E,F分别是AD,BD的中点,若EF=2,则菱形ABCD的周长是 16 .
【分析】先利用三角形中位线性质得到AB=4,然后根据菱形的性质计算菱形ABCD的周长.
解:∵E,F分别是AD,BD的中点,
∴EF为△ABD的中位线,
∴AB=2EF=4,
∵四边形ABCD为菱形,
∴AB=BC=CD=DA=4,
∴菱形ABCD的周长=4×4=16.
故答案为16.
14.某同学做掷硬币试验,正面朝上记为“正”,反面朝上记为“反”,结果统计如下:
次数 1 2 3 4 5 6 7 8 9 10
结果 反 正 正 反 正 正 反 正 正 反
则“正面朝上”的频数是 6 ;“反面朝上”的频率是 0.4 .
【分析】根据实验结果得出结论即可.
解:某同学做掷硬币试验,共抛了10次,6次正面朝上,4次反面朝上,则正面朝上的频数是6,反面朝上的频数是4,“反面朝上”的频率是:=0.4.
故答案是:6;0.4.
15.如图,一次函数y=kx+b的图象与坐标轴的交点坐标分别为A(0,2),B(﹣3,0),下列说法:①y随x的增大而减小;②b=﹣3;③关于x的方程kx+b=0的解为x=2;④关于x的不等式kx+b<0的解集x<﹣3.其中说法正确的有 ④ .
【分析】根据一次函数的性质,一次函数与一元一次方程的关系对各个说法分析判断即可得解.
解:①如图所示:y随x的增大而增大,故说法错误;
②由于一次函数y=kx+b的图象与y轴交点是(0,2),所以b=2,故说法错误;
③由于一次函数y=kx+b的图象与x轴的交点坐标是(﹣3,0),所以关于x的方程kx+b=0的解为x=﹣3,故说法错误;
④如图所示:关于x的不等式kx+b<0的解集x<﹣3,故说法正确.
综上所述,说法正确的结论是:④.
故答案是:④.
16.如图,某校的生物园形状是一个直角三角形,∠ACB=90°,AC=40m,BC=30m.现要修建一条水渠CD,D点在边AB上,若水渠的造价为800元/m,则修建水渠CD最少要 38400 元.
【分析】要使水渠造价最低,则CD最短,利用勾股定理求出AB的长度,利用等面积法求出CD即可.
解:当CD为斜边上的高时,CD最短,从而水渠造价最低,
∵∠ACB=90°,AC=40m,BC=30m,
∴AB===50m,
∵CD?AB=AC?BC,
即CD?100=80×60,
∴CD=48m,
此时,最低造价为38400元,
所以,CD长为48米,水渠的造价最低,其最低造价为38400元,
故答案为:38400.
三、解答题(本大题共86分)
17.已知正比例函数的图象经过点M(﹣1,5).
(1)求这个函数的表达式;
(2)若将这个函数的图象向上平移5个单位后,写出图象与y轴的交点坐标.
【分析】(1)利用待定系数法确定函数关系式;
(2)根据“上加下减”平移规律写出新直线方程,利用直线方程求得该图象与y轴的交点坐标.
解:(1)设函数表达式为y=kx,
因为它的图象经过点M(﹣1,5),则5=﹣k,
解得k=﹣5.
故所求的表达式为y=﹣5x.
(2)将函数y=﹣5x的图象向上平移5个单位后所得函数街系数为为y=﹣5x+5.
令x=0,则y=5.
所以该函数图象与y轴的交点坐标是(0,5).
18.如图,四边形ABCD中,AB=CD,∠ABC=90°,∠ADC=90°.求证:AD=BC.
【分析】根据直角三角形的定义得到△ABC和△CDA是直角三角形,根据全等三角形的判定和性质定理即可得到结论.
【解答】证明:∵∠ABC=90°,∠ADC=90°.
∴△ABC和△CDA是直角三角形,
在Rt△ABC和Rt△CDA中,
,
∴Rt△ABC≌Rt△CDA(HL),
∴AD=CB.
19.如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆(B)位置的坐标;
(2)若体育馆位置坐标为C(﹣3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
【分析】(1)利用点A的坐标画出直角坐标系;根据点的坐标的意义描出点B;
(2)利用三角形的面积得到△ABC的面积.
解:(1)建立直角坐标系如图所示:
图书馆(B)位置的坐标为(﹣3,﹣2);
(2)标出体育馆位置C如图所示,观察可得,△ABC中BC边长为5,BC边上的高为4,所以△ABC的面积为==10.
20.如图,在?ABCD中,E在BC的延长线上,且CE=BC,AE与CD相交于F.
(1)求证:AC=DE;
(2)若∠BAE=90°,线段AE与CD是什么关系?为什么?
【分析】(1)理由平行四边形的性质证得四边形ACED是平行四边形即可证得结论;
(2)判定四边形ACED是菱形后即可证得对角线互相垂直平分.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=CE AD∥BE,
又CE=BC,
∴AD=CE,
∴四边形ACED是平行四边形,
∴AC=DE;
(2)解:互相垂直平分;
理由:∵∠BAE=90°,BC=CE,
∴AC=CE,
∴四边形ACED是菱形,
∴AE与CD互相垂直平分.
21.为了提高学生书写汉字的能力,增强保护汉字的意识,育才学校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,决赛规则是:同时听写100个汉字,每正确听写出一个汉字得1分.若用x(分)表示学生成绩,结果50≤x≤100,将其按分数段分为五组,绘制出不完整表格及直方图.
组别 成绩x(分) 频数(人数) 频率
一 50≤x<60 2 0.04
二 60≤x<70 10 0.2
三 70≤x<80 14 b
四 80≤x<90 a 0.32
五 90≤x<100 8 0.16
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 50 名学生参加;
(2)求a,b的值,并补全右边的直方图;
(3)若决赛成绩不低于80分为优秀,求本次大赛的优秀率.
【分析】(1)根据表格中的数据可以求得本次决赛的学生数;
(2)根据(1)中决赛学生数,可以求得a、b的值;根据a的值,可以将频数分布直方图补充完整;
(3)根据表格中的数据可以求得本次大赛的优秀率.
解:(1)由表格可得,
本次决赛的学生数为:10÷0.2=50(名),
故答案为:50;
(2)a=50×0.32=16,b=14÷50=0.28,
补全的频数分布直方图如图所示,
(3)由表格可得,
决赛成绩不低于80分为优秀率为:(0.32+0.16)×100%=48%,
答:本次大赛的优秀率为48%.
22.如图,在Rt△ABC中,两锐角的平分线AD,BE相交于O,OF⊥AC于F,OG⊥BC于G.
(1)求证:四边形OGCF是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF的边长.
【分析】(1)根据有三个角是直角的四边形是矩形,可得四边形OGCF是矩形,根据角平分线的性质,可得OH与OF,OH与OG的关系,根据邻边相等的矩形是正方形,可得答案;
(2)由含30°角的直角三角形的性质和勾股定理求出AB和BC,根据全等三角形判定的HL定理证得Rt△AOH≌Rt△AOF得到AH=AF,设正方形OGCF的边长为x,则AH=AF=4﹣x,BH=BG=4﹣x,根据AB=AH+BH=8,解方程即可求出x.
【解答】(1)证明:过O作OH⊥AB于H点,
∵OF⊥AC于点F,OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD,BE分别是∠BAC,∠ABC的角平分线,OF⊥AC,OG⊥BC,
∴OG=OH=OF,
又四边形OGCF是矩形,
∴四边形OGCF是正方形;
(2)解:在Rt△ABC中,
∵∠BAC=60°,
∴∠ABC=90°﹣∠BAC=90°﹣60°=30°,
∴AC=AB,
∵AC=4,
∴AB=2AC=2×4=8,
∵AC2+BC2=AB2,
∴BC==4,
在Rt△AOH和Rt△AOF中,
,
∴Rt△AOH≌Rt△AOF(HL),
∴AH=AF,
设正方形OGCF的边长为x,
则AH=AF=4﹣x,BH=BG=4﹣x,
∴4﹣x+4﹣x=8,
∴x=2﹣2,
即正方形OGCF的边长为2﹣2.
23.周日,小明一家从家里出发去40公里的郊外野炊,小明和妹妹小红早上8:00骑自行车先走.爸爸和妈妈开车10:00出发,半小时追上小明和小红,随即小明和小红乘坐爸妈的车一起前往目的地.设小明和小红所用的时间为x(小时),小明和小红所走的路程为y1(公里),爸妈所走的路程为y2(公里),图中OCB表示y1与x之间的函数关系,线段AB表示y2与x之间的函数关系.
(1)爸妈开车的速度是每小时多少公里?
(2)求y1、y2与x的函数表达式.
(3)如果小明和小红中途不乘坐爸妈的车,继续骑车前往,12:00能到达目的地吗?说明理由.
【分析】(1)根据题意和函数图象可以求得爸妈开车的速度;
(2)利用待定系数法求出y2与x的函数表达式,根据题意可以求得点C的坐标,再用待定系数法分段求出y1与x之间的函数关系式,并写出自变量的取值范围;
(3)根据OC段的解析式可以求得小明和小红中途不乘坐爸妈的车,继续骑车前往所用时间,即可得出结论.
解:(1)由函数图象得:爸爸和妈妈开车到达目的地的时间为3﹣2=1(小时),
∴爸妈开车的速度是:40÷1=40(公里/小时),
答:爸妈开车的速度是每小时40公里;
(2)设y2=kx+b,从图中知其图象经过(2,0)和(3,40),
则,
解得 ,
∴y2=40x﹣80(2≤x≤3);
当x=2.5时,y2=20,所以C点为(2.5,20),
又设OC的解析式为y1=mx,
则2.5m=20,解得m=8,
则y1=8x(0≤x≤2.5),
CB段的解析式是y2相同,
所以 ;
(3)在直线OC上,当y=40时,x=5,这说明小明他们不乘坐爸妈的车,全程需要5个小时,即13:00才能到达,所以他们12:00不能到达.
24.如图,直线与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为x轴上一动点.
(1)填空:A点坐标是 (﹣8,0) ,B点的坐标是 (0,6) .
(2)当P是OA的中点时,四边形PCDO是 矩 形,其周长是 24 .
(3)当PC+PD最小时,求P点的坐标.
(4)是否存在P点,使△PCD是等腰三角形?若存在,请求出P点的坐标.
【分析】(1)对于,令=0,解得x=﹣8,令x=0,则y=6,即可求解;
(2)C、D的纵坐标相同,故CD∥OP,点C、P的横坐标相同,故CP∥OD,进而求解;
(3)作点C关于x轴的对称点C′(﹣4,﹣3),连接C′D交x轴于点P,则点P为所求点,进而求解;
(4)分PC=PD、PC=CD、PD=CD三种情况,分别求解即可.
解:(1)对于,令=0,解得x=﹣8,令x=0,则y=6,
故点A、B的坐标分别为(﹣8,0)、(0,6),
故答案为:(﹣8,0)、(0,6);
(2)∵C、D分别为线段AB、OB的中点,故点C、D的坐标分别为(﹣4,3)、(0,3),
∵P是OA的中点,故点P的坐标为(0,﹣4),
∵C、D的纵坐标相同,故CD∥OP,
点C、P的横坐标相同,故CP∥OD,
则四边形PCDO是平行四边形,而∠DOP=90°,
故四边形PCDO是矩形,
则四边形PCDO的周长=2(CD+CP)=2×(4+3)=24,
故答案为:矩,24;
(3)作点C关于x轴的对称点C′(﹣4,﹣3),连接C′D交x轴于点P,则点P为所求点,
设直线C′D的表达式为y=kx+b,
则,解得,
故直线C′D的表达式为y=x+3,
令y=x+3=0,解得x=﹣2,
故点P的坐标为(﹣2,0);
(4)设点P(x,0),
由点P、C、D的坐标得:PC2=(x+4)2+9,PD2=x2+9,CD2=16,
当PC=PD时,即(x+4)2+9=x2+9,解得x=﹣2,
当PC=CD时,则(x+4)2+9=16,解得x=﹣4±,
当PD=CD时,则x2+9=16,解得x=,
综上,点P的坐标为:(﹣2,0)(,0)(,0)(,0).
同课章节目录
