2020-2021学年上海市浦东新区川沙七年级(下)期末数学试卷 (word版含解析)
文档属性
| 名称 | 2020-2021学年上海市浦东新区川沙七年级(下)期末数学试卷 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览



文档简介
2020-2021学年上海市浦东新区川沙七年级(下)期末数学试卷
一、单项选择题(每题3分,满分18分).
1.下列说法正确的是( )
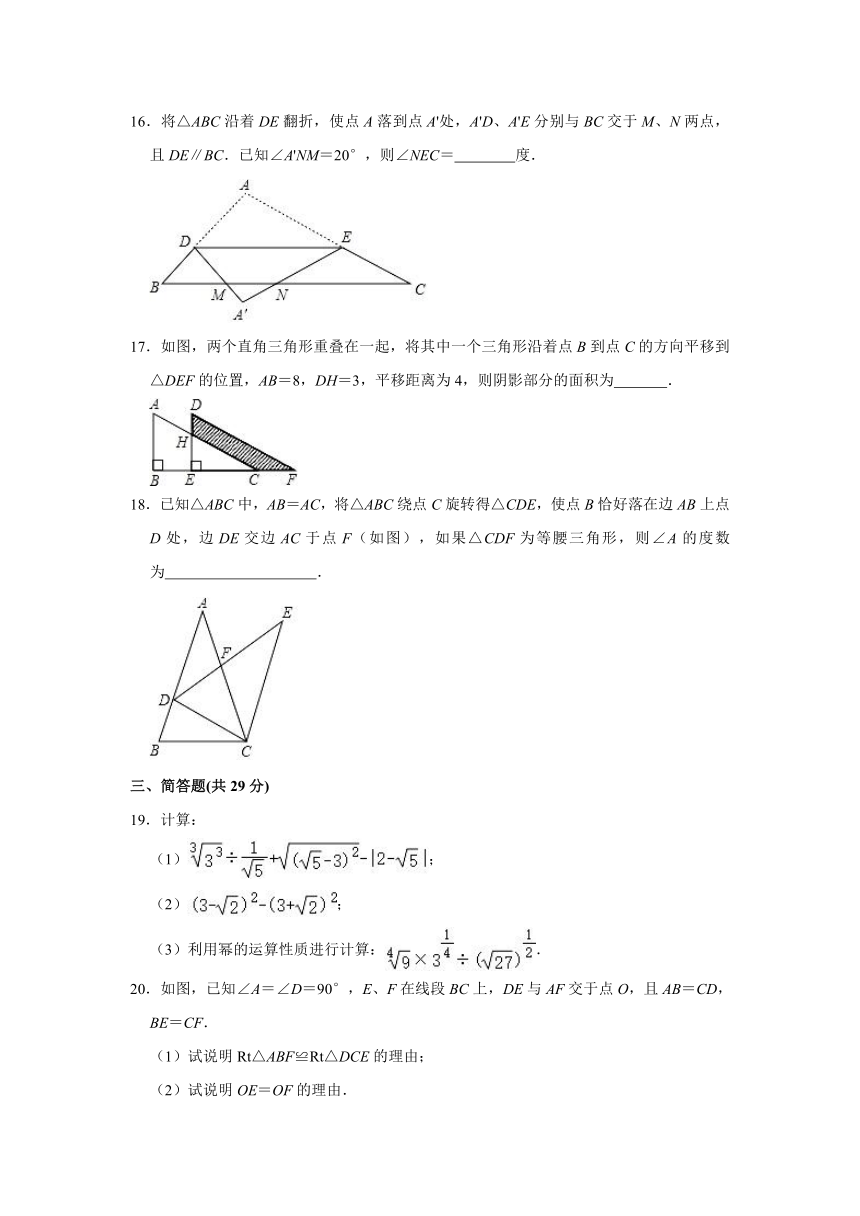
A.无限小数都是无理数
B.无理数都是无限小数
C.有理数只是有限小数
D.实数可以分为正实数和负实数
2.下列计算正确的是( )
A. B. C. D.
3.平面直角坐标系中,将点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2) C.(﹣6,﹣1) D.(0,﹣1)
4.如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是
①△BDF、△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )
A.③④ B.①② C.①②③ D.②③④
5.如图,在△ABC和△ABD中,已知∠CAB=∠DAB,在不添加任何辅助线的前提下,要使△ABC≌△ABD,只需再添加的一个条件不可以是( )
A.AC=AD B.BC=BD C.∠C=∠D D.∠CBE=∠DBE
6.△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2.5 B.3 C.2.25或3 D.1或5
二、填空题(每题2分,满分24分)
7.在实数①,②π,③2.131131113,④,⑤0,⑥中,无理数是 (填序号).
8.的5次方根是 .
9.近似数0.0320有 个有效数字.
10.计算:= .
11.比较大小: ﹣4(填“<”或“=”或“>”).
12.数轴上表示数和的两点之间的距离为 .
13.已知点P(3m﹣6,m+1),A(﹣1,2),直线PA与x轴平行,则点P的坐标为 .
14.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=56°,∠2=29°,则∠A的度数为 度.
15.如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFD的度数为 度.
16.将△ABC沿着DE翻折,使点A落到点A'处,A'D、A'E分别与BC交于M、N两点,且DE∥BC.已知∠A'NM=20°,则∠NEC= 度.
17.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=8,DH=3,平移距离为4,则阴影部分的面积为 .
18.已知△ABC中,AB=AC,将△ABC绕点C旋转得△CDE,使点B恰好落在边AB上点D处,边DE交边AC于点F(如图),如果△CDF为等腰三角形,则∠A的度数为 .
三、简答题(共29分)
19.计算:
(1);
(2);
(3)利用幂的运算性质进行计算:.
20.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
(1)试说明Rt△ABF≌Rt△DCE的理由;
(2)试说明OE=OF的理由.
21.已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ ( )
所以∠B+∠BDE=180° ( )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° ( )
所以 ∥ ( )
所以∠1=∠2 ( ).
22.如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
解:EF、BC的位置关系是 .
说理如下:
因为AD是∠BAC的角平分线(已知)
所以∠1=∠2.
在△AED和△ACD中,
所以△AED≌△ACD(S.A.S).
得 (全等三角形的对应边相等).
(完成以下说理过程)
四、解答题(共29分)
23.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
24.如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
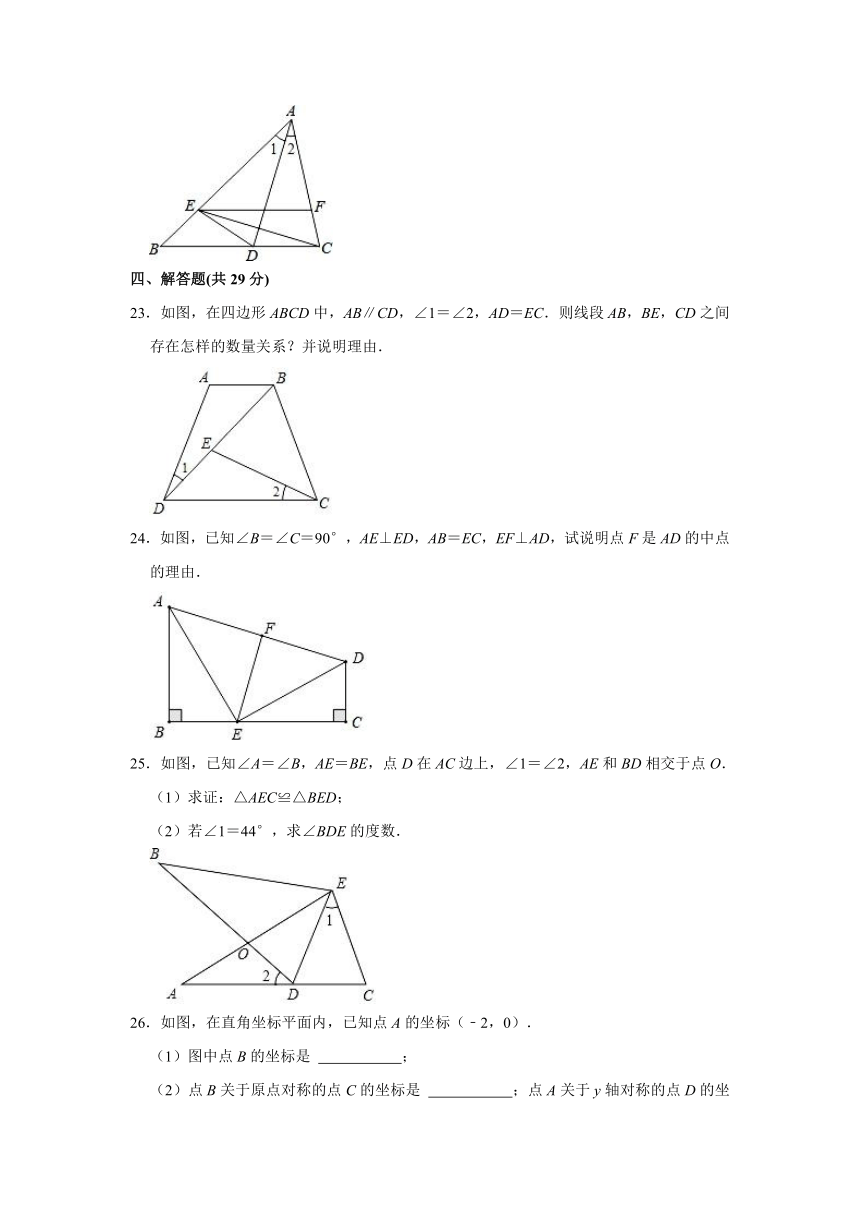
25.如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=44°,求∠BDE的度数.
26.如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是 ;
(2)点B关于原点对称的点C的坐标是 ;点A关于y轴对称的点D的坐标是 ;
(3)四边形ABDC的面积是 ;
(4)在y轴上找一点F,使S△ADF=S△ABC,那么点F的所有可能位置是 .
27.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE,并延长AD交BE于点P;
(1)求证:AD=BE;
(2)试说明AD⊥BE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
参考答案
一、单项选择题(每小题3分,满分18分)
1.下列说法正确的是( )
A.无限小数都是无理数
B.无理数都是无限小数
C.有理数只是有限小数
D.实数可以分为正实数和负实数
解:A、无限小数都不一定是无理数,其中无限循环小数为有理数,故本选项错误.
B、根据无理数的定义,无理数都是无限小数,故本选项正确.
C、有理数不只是有限小数,例如无限循环小数,故本选项错误;
D、实数可以分为正实数和负实数和0,故本选项错误;
故选:B.
2.下列计算正确的是( )
A. B. C. D.
解:A、()2=3,故此选项正确;
B、±=±3,故此选项正错误;
C、=4,故此选项正错误;
D、=3,故此选项正错误;
故选:A.
3.平面直角坐标系中,将点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2) C.(﹣6,﹣1) D.(0,﹣1)
解:点A的坐标为(﹣3,﹣5),将点A向上平移4个单位,再向左平移3个单位到点B,
点B的横坐标是﹣3﹣3=﹣6,纵坐标为﹣5+4=﹣1,即(﹣6,﹣1).
故选:C.
4.如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是
①△BDF、△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )
A.③④ B.①② C.①②③ D.②③④
解:∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵BF是∠ABC的平分线,CF是∠ACB的平分线,
∴∠FBC=∠DFB,∠FCE=∠FCB,
∵∠DBF=∠DFB,∠EFC=∠ECF,
∴△DFB,△FEC都是等腰三角形.
∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,
∴△ADE的周长AD+AE+DE=AD+AE+DB+EC=AB+AC.
故选:C.
5.如图,在△ABC和△ABD中,已知∠CAB=∠DAB,在不添加任何辅助线的前提下,要使△ABC≌△ABD,只需再添加的一个条件不可以是( )
A.AC=AD B.BC=BD C.∠C=∠D D.∠CBE=∠DBE
解:A、添加AC=AD,利用SAS即可得到两三角形全等,不符合题意;
B、添加BC=BD,不能判定两三角形全等,符合题意;
C、添加∠D=∠C,利用AAS即可得到两三角形全等,不符合题意;
D、添加∠CBE=∠DBE,利用ASA即可得到两三角形全等,不符合题意;
故选:B.
6.△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2.5 B.3 C.2.25或3 D.1或5
解:∵△ABC中,AB=AC=12厘米,点D为AB的中点,
∴BD=6厘米,
若△BPD≌△CPQ,则需BD=CQ=6厘米,BP=CP=BC=×9=4.5(厘米),
∵点Q的运动速度为3厘米/秒,
∴点Q的运动时间为:6÷3=2(s),
∴v=4.5÷2=2.25(厘米/秒);
若△BPD≌△CQP,则需CP=BD=6厘米,BP=CQ,
∴,
解得:v=3;
∴v的值为:2.25或3,
故选:C.
二、填空题(每题2分,满分24分)
7.在实数①,②π,③2.131131113,④,⑤0,⑥中,无理数是 ②④ (填序号).
解:①﹣是分数,属于有理数;
②π是无理数;
③2.131131113是有限小数,属于有理数;
④是无理数;
⑤0是整数,属于有理数;
⑥=﹣2是有理数;
无理数是②π,④.
故答案为:②④.
8.的5次方根是 .
解:=,
故答案为:.
9.近似数0.0320有 3 个有效数字.
解:近似数0.0320有3个有效数字,
故答案为:3.
10.计算:= ﹣4 .
解:原式=.
11.比较大小: > ﹣4(填“<”或“=”或“>”).
解:∵4=2×2=2,
2<2,
∴>﹣4.
故答案为>.
12.数轴上表示数和的两点之间的距离为 .
解:﹣(﹣5)
=+5
=,
故答案为:.
13.已知点P(3m﹣6,m+1),A(﹣1,2),直线PA与x轴平行,则点P的坐标为 (﹣3,2) .
解:∵点P(3m﹣6,m+1)在过点A(﹣1,2)且与x轴平行的直线上,
∴m+1=2,
解得m=1,
∴3m﹣6=3×1﹣6=﹣3,
∴m+1=1+1=2,
∴点P的坐标为(﹣3,2),
故答案为:(﹣3,2).
14.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=56°,∠2=29°,则∠A的度数为 27 度.
解:如图,
∵直线a∥b,
∴∠3=∠1,
∵∠1=56°,
∴∠3=56°,
∵∠3=∠2+∠A,∠2=29°,
∴∠A=∠3﹣∠2=56°﹣29°=27°.
故答案为:27.
15.如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFD的度数为 60 度.
解:∵△ABC是等边三角形,
∴AB=AC,∠ABE=∠BCD,∠ABF+∠CBF=60°,
∴在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAF=∠CBF,
∴∠AFD=∠ABF+∠BAF=∠ABF+∠CBF=60°.
16.将△ABC沿着DE翻折,使点A落到点A'处,A'D、A'E分别与BC交于M、N两点,且DE∥BC.已知∠A'NM=20°,则∠NEC= 140 度.
解:∵∠A′NM=20°,∠CNE=∠A′MN,
∴∠CNE=20°,
∵DE∥BC,
∴∠DEN=∠CNE=20°,
由翻折性质得:∠AED=∠DEN=20°,
∴∠AEN=40°,
∴∠NEC=180°﹣∠AEN=180°﹣40°=140°.
故答案为:140.
17.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=8,DH=3,平移距离为4,则阴影部分的面积为 26 .
解:∵△ABC沿着点B到点C的方向平移到△DEF的位置,
∴△ABC≌△DEF,
∴阴影部分面积等于梯形ABEH的面积,
由平移的性质得,DE=AB,BE=4,
∵AB=8,DH=3,
∴HE=DE﹣DH=8﹣3=5,
∴阴影部分的面积=×(5+8)×4=26.
故答案为:26.
18.已知△ABC中,AB=AC,将△ABC绕点C旋转得△CDE,使点B恰好落在边AB上点D处,边DE交边AC于点F(如图),如果△CDF为等腰三角形,则∠A的度数为 36°或 .
解:如图,设∠B=x,
∵AB=AC,
∴∠ACB=∠B=x
∴∠A=180°﹣2x,
∵△ABC绕点C旋转得△CDE,使点B恰好落在边AB上点D处,
∴CB=CD,∠2=∠B=x,
∴∠1=∠B=x,
∴∠5=180°﹣2x,∠3=∠A+∠5=360°﹣4x,
当CD=CF时,△CDF为等腰三角形,即∠2=∠3=x,则x=360°﹣4x,解得x=72°,此时∠A=180°﹣2x=36°;
当CD=DF时,△CDF为等腰三角形,即∠4=∠3,而∠2+∠3+∠4=180°,则x+2(360°﹣4x)=180°,解得x=,此时∠A=180°﹣2x=;
当CF=DF时,△CDF为等腰三角形,即∠2=∠4=x,而∠2+∠3+∠4=180°,则x+x+360°﹣2x=180°,无解,故舍去.
综上所述,△CDF为等腰三角形时∠A的度数为36°或.
故答案为36°或.
三、简答题(共29分)
19.计算:
(1);
(2);
(3)利用幂的运算性质进行计算:.
解:(1)=3×+3﹣﹣(﹣2)=3+3﹣﹣+2=+5;
(2)=9+2﹣6﹣(9+2+6)=﹣12;
(3)=×÷=÷=÷=÷=1.
20.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
(1)试说明Rt△ABF≌Rt△DCE的理由;
(2)试说明OE=OF的理由.
解:(1)∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL);
(2)∵Rt△ABF≌Rt△DCE,
∴∠AFB=∠DEC,
∴OE=OF.
21.已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 DE ∥ BC ( 同位角相等,两直线平行 )
所以∠B+∠BDE=180° ( 两直线平行,同旁内角互补 )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° ( 等量代换 )
所以 EF ∥ AB ( 同旁内角互补,两直线平行, )
所以∠1=∠2 ( 两直线平行,内错角相等 ).
解:因为∠AED=∠C(已知)
所以 DE∥BC( 同位角相等,两直线平行)
所以∠B+∠BDE=180° ( 两直线平行,同旁内角互补)
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° (等量代换 )
所以 EF∥AB(同旁内角互补,两直线平行 )
所以∠1=∠2 ( 两直线平行,内错角相等).
故答案为:DE,BC,同位角相等,两直线平行,两直线平行,同旁内角互补,等量代换 EF,AB,同旁内角互补,两直线平行,两直线平行,内错角相等.
22.如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
解:EF、BC的位置关系是 EF∥BC .
说理如下:
因为AD是∠BAC的角平分线(已知)
所以∠1=∠2.
在△AED和△ACD中,
所以△AED≌△ACD(S.A.S).
得 DE=DC (全等三角形的对应边相等).
(完成以下说理过程)
解:EF、BC的位置关系是EF∥BC.
理由如下:
如图,
∵AD是∠BAC的角平分线(已知)
∴∠1=∠2.
在△AED和△ACD中,
∴△AED≌△ACD(SAS).
∴DE=DC (全等三角形的对应边相等),
∴∠3=∠4.
∵EC平分∠DEF(已知),
∴∠3=∠5.
∴∠4=∠5.
所以EF∥BC(内错角相等,两直线平行).
故答案为:EF∥BC,DE=DC.
四、解答题(共29分)
23.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
解:AB+BE=CD,理由如下:
∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴AB=DE,BD=CD,
∵DE+BE=BD,
∴AB+BE=CD.
24.如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
解:∵AE⊥DE,
∴∠AED=90°,
又∵∠B=90°,
∴∠B=∠AED,
∵∠AEC=∠B+∠BAE,
即∠AED+∠DEC=∠B+∠BAE,
∴∠BAE=∠DEC,
在△ABE与△ECD中,
,
∴△ABE≌△ECD(ASA),
∴AE=ED,
∵EF⊥AD,
∴点F是AD的中点.
25.如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=44°,求∠BDE的度数.
【解答】(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA);
(2)解:∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=44°,
∴∠C=∠EDC=68°,
∴∠BDE=∠C=68°.
26.如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是 (﹣3,4) ;
(2)点B关于原点对称的点C的坐标是 (3,﹣4) ;点A关于y轴对称的点D的坐标是 (2,0) ;
(3)四边形ABDC的面积是 16 ;
(4)在y轴上找一点F,使S△ADF=S△ABC,那么点F的所有可能位置是 (0,4)或(0,﹣4) .
解:如图,
(1)过点B作x轴的垂线,垂足所对应的数为﹣3,因此点B的横坐标为﹣3,
过点B作y轴的垂线,垂足所对应的数为4,因此点B的纵坐标为4,
所以点B(﹣3,4);
故答案为:(﹣3,4);
(2)由于关于原点对称的两个点坐标纵横坐标均为互为相反数,
所以点B(﹣3,4)关于原点对称点C(3,﹣4),
由于关于y轴对称的两个点,其横坐标互为相反数,其纵坐标不变,
所以点A(﹣2,0)关于y轴对称点D(2,0),
故答案为:(3,﹣4),(2,0);
(3)S平行四边形ABCD=2S△ABD=2××4×4=16,
故答案为:16;
(4)因为S△ABC=S平行四边形ABCD=8=S△ADF,
所以AD?OF=8,
∴OF=4,
又∵点F在y轴上,
∴点F(0,4)或(0,﹣4),
故答案为:(0,4)或(0,﹣4).
27.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE,并延长AD交BE于点P;
(1)求证:AD=BE;
(2)试说明AD⊥BE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
解:(1)∵BC⊥AE,∠BAE=45°,
∴∠CBA=∠CAB,
∴BC=CA,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BDP=∠ADC,
∴∠BPD=∠DCA=90°,
∴AD⊥BE.
(3)AD⊥BE不发生变化.
理由:如图(2),
∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BFP=∠AFC,
∴∠BPF=∠ACF=90°,
∴AD⊥BE.
一、单项选择题(每题3分,满分18分).
1.下列说法正确的是( )
A.无限小数都是无理数
B.无理数都是无限小数
C.有理数只是有限小数
D.实数可以分为正实数和负实数
2.下列计算正确的是( )
A. B. C. D.
3.平面直角坐标系中,将点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2) C.(﹣6,﹣1) D.(0,﹣1)
4.如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是
①△BDF、△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )
A.③④ B.①② C.①②③ D.②③④
5.如图,在△ABC和△ABD中,已知∠CAB=∠DAB,在不添加任何辅助线的前提下,要使△ABC≌△ABD,只需再添加的一个条件不可以是( )
A.AC=AD B.BC=BD C.∠C=∠D D.∠CBE=∠DBE
6.△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2.5 B.3 C.2.25或3 D.1或5
二、填空题(每题2分,满分24分)
7.在实数①,②π,③2.131131113,④,⑤0,⑥中,无理数是 (填序号).
8.的5次方根是 .
9.近似数0.0320有 个有效数字.
10.计算:= .
11.比较大小: ﹣4(填“<”或“=”或“>”).
12.数轴上表示数和的两点之间的距离为 .
13.已知点P(3m﹣6,m+1),A(﹣1,2),直线PA与x轴平行,则点P的坐标为 .
14.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=56°,∠2=29°,则∠A的度数为 度.
15.如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFD的度数为 度.
16.将△ABC沿着DE翻折,使点A落到点A'处,A'D、A'E分别与BC交于M、N两点,且DE∥BC.已知∠A'NM=20°,则∠NEC= 度.
17.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=8,DH=3,平移距离为4,则阴影部分的面积为 .
18.已知△ABC中,AB=AC,将△ABC绕点C旋转得△CDE,使点B恰好落在边AB上点D处,边DE交边AC于点F(如图),如果△CDF为等腰三角形,则∠A的度数为 .
三、简答题(共29分)
19.计算:
(1);
(2);
(3)利用幂的运算性质进行计算:.
20.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
(1)试说明Rt△ABF≌Rt△DCE的理由;
(2)试说明OE=OF的理由.
21.已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 ∥ ( )
所以∠B+∠BDE=180° ( )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° ( )
所以 ∥ ( )
所以∠1=∠2 ( ).
22.如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
解:EF、BC的位置关系是 .
说理如下:
因为AD是∠BAC的角平分线(已知)
所以∠1=∠2.
在△AED和△ACD中,
所以△AED≌△ACD(S.A.S).
得 (全等三角形的对应边相等).
(完成以下说理过程)
四、解答题(共29分)
23.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
24.如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
25.如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=44°,求∠BDE的度数.
26.如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是 ;
(2)点B关于原点对称的点C的坐标是 ;点A关于y轴对称的点D的坐标是 ;
(3)四边形ABDC的面积是 ;
(4)在y轴上找一点F,使S△ADF=S△ABC,那么点F的所有可能位置是 .
27.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE,并延长AD交BE于点P;
(1)求证:AD=BE;
(2)试说明AD⊥BE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
参考答案
一、单项选择题(每小题3分,满分18分)
1.下列说法正确的是( )
A.无限小数都是无理数
B.无理数都是无限小数
C.有理数只是有限小数
D.实数可以分为正实数和负实数
解:A、无限小数都不一定是无理数,其中无限循环小数为有理数,故本选项错误.
B、根据无理数的定义,无理数都是无限小数,故本选项正确.
C、有理数不只是有限小数,例如无限循环小数,故本选项错误;
D、实数可以分为正实数和负实数和0,故本选项错误;
故选:B.
2.下列计算正确的是( )
A. B. C. D.
解:A、()2=3,故此选项正确;
B、±=±3,故此选项正错误;
C、=4,故此选项正错误;
D、=3,故此选项正错误;
故选:A.
3.平面直角坐标系中,将点A(﹣3,﹣5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,﹣8) B.(1,﹣2) C.(﹣6,﹣1) D.(0,﹣1)
解:点A的坐标为(﹣3,﹣5),将点A向上平移4个单位,再向左平移3个单位到点B,
点B的横坐标是﹣3﹣3=﹣6,纵坐标为﹣5+4=﹣1,即(﹣6,﹣1).
故选:C.
4.如图,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是
①△BDF、△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )
A.③④ B.①② C.①②③ D.②③④
解:∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵BF是∠ABC的平分线,CF是∠ACB的平分线,
∴∠FBC=∠DFB,∠FCE=∠FCB,
∵∠DBF=∠DFB,∠EFC=∠ECF,
∴△DFB,△FEC都是等腰三角形.
∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,
∴△ADE的周长AD+AE+DE=AD+AE+DB+EC=AB+AC.
故选:C.
5.如图,在△ABC和△ABD中,已知∠CAB=∠DAB,在不添加任何辅助线的前提下,要使△ABC≌△ABD,只需再添加的一个条件不可以是( )
A.AC=AD B.BC=BD C.∠C=∠D D.∠CBE=∠DBE
解:A、添加AC=AD,利用SAS即可得到两三角形全等,不符合题意;
B、添加BC=BD,不能判定两三角形全等,符合题意;
C、添加∠D=∠C,利用AAS即可得到两三角形全等,不符合题意;
D、添加∠CBE=∠DBE,利用ASA即可得到两三角形全等,不符合题意;
故选:B.
6.△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
A.2.5 B.3 C.2.25或3 D.1或5
解:∵△ABC中,AB=AC=12厘米,点D为AB的中点,
∴BD=6厘米,
若△BPD≌△CPQ,则需BD=CQ=6厘米,BP=CP=BC=×9=4.5(厘米),
∵点Q的运动速度为3厘米/秒,
∴点Q的运动时间为:6÷3=2(s),
∴v=4.5÷2=2.25(厘米/秒);
若△BPD≌△CQP,则需CP=BD=6厘米,BP=CQ,
∴,
解得:v=3;
∴v的值为:2.25或3,
故选:C.
二、填空题(每题2分,满分24分)
7.在实数①,②π,③2.131131113,④,⑤0,⑥中,无理数是 ②④ (填序号).
解:①﹣是分数,属于有理数;
②π是无理数;
③2.131131113是有限小数,属于有理数;
④是无理数;
⑤0是整数,属于有理数;
⑥=﹣2是有理数;
无理数是②π,④.
故答案为:②④.
8.的5次方根是 .
解:=,
故答案为:.
9.近似数0.0320有 3 个有效数字.
解:近似数0.0320有3个有效数字,
故答案为:3.
10.计算:= ﹣4 .
解:原式=.
11.比较大小: > ﹣4(填“<”或“=”或“>”).
解:∵4=2×2=2,
2<2,
∴>﹣4.
故答案为>.
12.数轴上表示数和的两点之间的距离为 .
解:﹣(﹣5)
=+5
=,
故答案为:.
13.已知点P(3m﹣6,m+1),A(﹣1,2),直线PA与x轴平行,则点P的坐标为 (﹣3,2) .
解:∵点P(3m﹣6,m+1)在过点A(﹣1,2)且与x轴平行的直线上,
∴m+1=2,
解得m=1,
∴3m﹣6=3×1﹣6=﹣3,
∴m+1=1+1=2,
∴点P的坐标为(﹣3,2),
故答案为:(﹣3,2).
14.如图,直线a∥b,在Rt△ABC中,点C在直线a上,若∠1=56°,∠2=29°,则∠A的度数为 27 度.
解:如图,
∵直线a∥b,
∴∠3=∠1,
∵∠1=56°,
∴∠3=56°,
∵∠3=∠2+∠A,∠2=29°,
∴∠A=∠3﹣∠2=56°﹣29°=27°.
故答案为:27.
15.如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,则∠AFD的度数为 60 度.
解:∵△ABC是等边三角形,
∴AB=AC,∠ABE=∠BCD,∠ABF+∠CBF=60°,
∴在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAF=∠CBF,
∴∠AFD=∠ABF+∠BAF=∠ABF+∠CBF=60°.
16.将△ABC沿着DE翻折,使点A落到点A'处,A'D、A'E分别与BC交于M、N两点,且DE∥BC.已知∠A'NM=20°,则∠NEC= 140 度.
解:∵∠A′NM=20°,∠CNE=∠A′MN,
∴∠CNE=20°,
∵DE∥BC,
∴∠DEN=∠CNE=20°,
由翻折性质得:∠AED=∠DEN=20°,
∴∠AEN=40°,
∴∠NEC=180°﹣∠AEN=180°﹣40°=140°.
故答案为:140.
17.如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=8,DH=3,平移距离为4,则阴影部分的面积为 26 .
解:∵△ABC沿着点B到点C的方向平移到△DEF的位置,
∴△ABC≌△DEF,
∴阴影部分面积等于梯形ABEH的面积,
由平移的性质得,DE=AB,BE=4,
∵AB=8,DH=3,
∴HE=DE﹣DH=8﹣3=5,
∴阴影部分的面积=×(5+8)×4=26.
故答案为:26.
18.已知△ABC中,AB=AC,将△ABC绕点C旋转得△CDE,使点B恰好落在边AB上点D处,边DE交边AC于点F(如图),如果△CDF为等腰三角形,则∠A的度数为 36°或 .
解:如图,设∠B=x,
∵AB=AC,
∴∠ACB=∠B=x
∴∠A=180°﹣2x,
∵△ABC绕点C旋转得△CDE,使点B恰好落在边AB上点D处,
∴CB=CD,∠2=∠B=x,
∴∠1=∠B=x,
∴∠5=180°﹣2x,∠3=∠A+∠5=360°﹣4x,
当CD=CF时,△CDF为等腰三角形,即∠2=∠3=x,则x=360°﹣4x,解得x=72°,此时∠A=180°﹣2x=36°;
当CD=DF时,△CDF为等腰三角形,即∠4=∠3,而∠2+∠3+∠4=180°,则x+2(360°﹣4x)=180°,解得x=,此时∠A=180°﹣2x=;
当CF=DF时,△CDF为等腰三角形,即∠2=∠4=x,而∠2+∠3+∠4=180°,则x+x+360°﹣2x=180°,无解,故舍去.
综上所述,△CDF为等腰三角形时∠A的度数为36°或.
故答案为36°或.
三、简答题(共29分)
19.计算:
(1);
(2);
(3)利用幂的运算性质进行计算:.
解:(1)=3×+3﹣﹣(﹣2)=3+3﹣﹣+2=+5;
(2)=9+2﹣6﹣(9+2+6)=﹣12;
(3)=×÷=÷=÷=÷=1.
20.如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.
(1)试说明Rt△ABF≌Rt△DCE的理由;
(2)试说明OE=OF的理由.
解:(1)∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在Rt△ABF和Rt△DCE中,
,
∴Rt△ABF≌Rt△DCE(HL);
(2)∵Rt△ABF≌Rt△DCE,
∴∠AFB=∠DEC,
∴OE=OF.
21.已知:如图∠AED=∠C,∠DEF=∠B,请你说明∠1与∠2相等吗?为什么?
解:因为∠AED=∠C(已知)
所以 DE ∥ BC ( 同位角相等,两直线平行 )
所以∠B+∠BDE=180° ( 两直线平行,同旁内角互补 )
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° ( 等量代换 )
所以 EF ∥ AB ( 同旁内角互补,两直线平行, )
所以∠1=∠2 ( 两直线平行,内错角相等 ).
解:因为∠AED=∠C(已知)
所以 DE∥BC( 同位角相等,两直线平行)
所以∠B+∠BDE=180° ( 两直线平行,同旁内角互补)
因为∠DEF=∠B(已知)
所以∠DEF+∠BDE=180° (等量代换 )
所以 EF∥AB(同旁内角互补,两直线平行 )
所以∠1=∠2 ( 两直线平行,内错角相等).
故答案为:DE,BC,同位角相等,两直线平行,两直线平行,同旁内角互补,等量代换 EF,AB,同旁内角互补,两直线平行,两直线平行,内错角相等.
22.如图,在△ABC中,已知AD平分∠BAC,E是边AB上的一点,AE=AC,F是边AC上的一点,联结DE、CE、FE,当EC平分∠DEF时,猜测EF、BC的位置关系,并说明理由.
解:EF、BC的位置关系是 EF∥BC .
说理如下:
因为AD是∠BAC的角平分线(已知)
所以∠1=∠2.
在△AED和△ACD中,
所以△AED≌△ACD(S.A.S).
得 DE=DC (全等三角形的对应边相等).
(完成以下说理过程)
解:EF、BC的位置关系是EF∥BC.
理由如下:
如图,
∵AD是∠BAC的角平分线(已知)
∴∠1=∠2.
在△AED和△ACD中,
∴△AED≌△ACD(SAS).
∴DE=DC (全等三角形的对应边相等),
∴∠3=∠4.
∵EC平分∠DEF(已知),
∴∠3=∠5.
∴∠4=∠5.
所以EF∥BC(内错角相等,两直线平行).
故答案为:EF∥BC,DE=DC.
四、解答题(共29分)
23.如图,在四边形ABCD中,AB∥CD,∠1=∠2,AD=EC.则线段AB,BE,CD之间存在怎样的数量关系?并说明理由.
解:AB+BE=CD,理由如下:
∵AB∥CD,
∴∠ABD=∠EDC,
在△ABD和△EDC中,
,
∴△ABD≌△EDC(AAS),
∴AB=DE,BD=CD,
∵DE+BE=BD,
∴AB+BE=CD.
24.如图,已知∠B=∠C=90°,AE⊥ED,AB=EC,EF⊥AD,试说明点F是AD的中点的理由.
解:∵AE⊥DE,
∴∠AED=90°,
又∵∠B=90°,
∴∠B=∠AED,
∵∠AEC=∠B+∠BAE,
即∠AED+∠DEC=∠B+∠BAE,
∴∠BAE=∠DEC,
在△ABE与△ECD中,
,
∴△ABE≌△ECD(ASA),
∴AE=ED,
∵EF⊥AD,
∴点F是AD的中点.
25.如图,已知∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=44°,求∠BDE的度数.
【解答】(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA);
(2)解:∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=44°,
∴∠C=∠EDC=68°,
∴∠BDE=∠C=68°.
26.如图,在直角坐标平面内,已知点A的坐标(﹣2,0).
(1)图中点B的坐标是 (﹣3,4) ;
(2)点B关于原点对称的点C的坐标是 (3,﹣4) ;点A关于y轴对称的点D的坐标是 (2,0) ;
(3)四边形ABDC的面积是 16 ;
(4)在y轴上找一点F,使S△ADF=S△ABC,那么点F的所有可能位置是 (0,4)或(0,﹣4) .
解:如图,
(1)过点B作x轴的垂线,垂足所对应的数为﹣3,因此点B的横坐标为﹣3,
过点B作y轴的垂线,垂足所对应的数为4,因此点B的纵坐标为4,
所以点B(﹣3,4);
故答案为:(﹣3,4);
(2)由于关于原点对称的两个点坐标纵横坐标均为互为相反数,
所以点B(﹣3,4)关于原点对称点C(3,﹣4),
由于关于y轴对称的两个点,其横坐标互为相反数,其纵坐标不变,
所以点A(﹣2,0)关于y轴对称点D(2,0),
故答案为:(3,﹣4),(2,0);
(3)S平行四边形ABCD=2S△ABD=2××4×4=16,
故答案为:16;
(4)因为S△ABC=S平行四边形ABCD=8=S△ADF,
所以AD?OF=8,
∴OF=4,
又∵点F在y轴上,
∴点F(0,4)或(0,﹣4),
故答案为:(0,4)或(0,﹣4).
27.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE,并延长AD交BE于点P;
(1)求证:AD=BE;
(2)试说明AD⊥BE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
解:(1)∵BC⊥AE,∠BAE=45°,
∴∠CBA=∠CAB,
∴BC=CA,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BDP=∠ADC,
∴∠BPD=∠DCA=90°,
∴AD⊥BE.
(3)AD⊥BE不发生变化.
理由:如图(2),
∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BFP=∠AFC,
∴∠BPF=∠ACF=90°,
∴AD⊥BE.
同课章节目录
