八年级下册第二十章 数据的分析单元测试
文档属性
| 名称 | 八年级下册第二十章 数据的分析单元测试 |
|
|
| 格式 | zip | ||
| 文件大小 | 120.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-29 00:00:00 | ||
图片预览

文档简介
十中英才第二十章单元测试卷
姓名:_________ 得分:_______
一、选择题:(每题4分,共40分)
月用水量(吨) 5 6 7
户数 2 6 2
1. 2011年春某市发生了严重干旱,市政府号召居民节约用水,为了解居民用水情况,某小区随机抽查了10户家庭的月用水量,结果如下表:则关于这10户家庭的月用水量,下列说法错误的是( )
A.众数是6 B.极差是2
C.平均数是6 D.方差是4
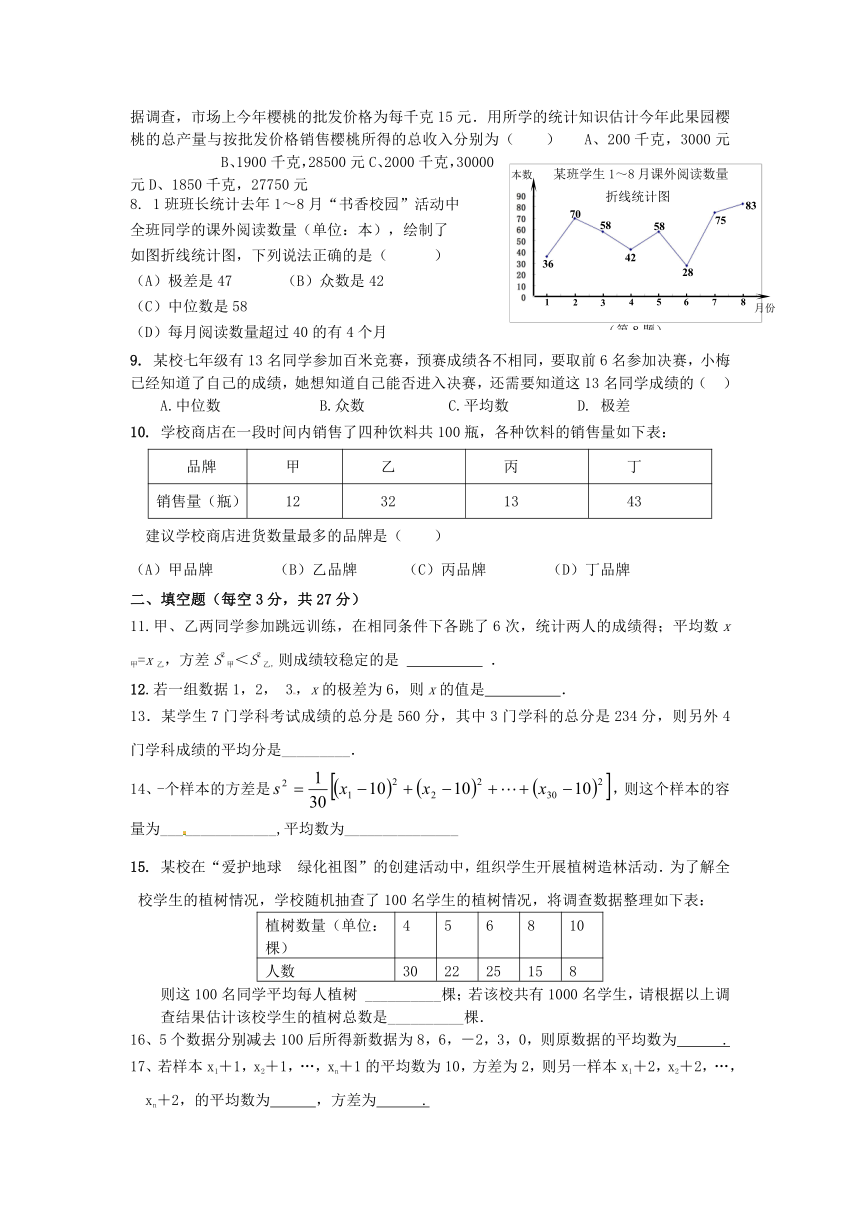
2、学校快餐店有2元,3元,4元三种价格的饭菜供师生选择(每人限购一份).如图是某月的销售情况统计图,则该校师生购买饭菜费用的平均数和众数是( )
A.2.95元,3元 B.3元,3元 C.3元,4元 D.2.95元,4元
3、如图,某路口统计的某个时段来往汽车的车速(单位:千米/小时)情况,据统计图,这组车速数据的众数和中位数分别是( )
A、60千米/小时,60千米/小时 B、58千米/小时,60千米/小时
C、60千米/小时,58千米/小时 D、58千米/小时,58千米/小时
4. 某住宅小区六月份1日至5日每天用水量变化情况如图所示,那么这5天的用水量
的中位数是( )A.30吨 B.31吨 C.32吨 D.33吨
第2题 第3题 第4题
5、以下说法中正确的是( )
A.极差较大的一组数据方差也大. B.分别用一组数据中的每一个减去平均数,再将所得的差相加,若和为零,则方差为零C.在一组数据中去掉一个等于平均数的数,这组数据的方差不变. D.如果一组数据的方差等于零,则这组数据中的每一个彼此相等
6.如果一组数据,,…,的方差是2,那么一组新数据2,2,…,2的方差是( ) A. 2 B. 4 C. 8 D. 16
7、李大伯承包了一个果园,种植了100棵樱桃树,今年已进入收获期.收获时,从中任选并采摘了10棵树的樱桃,分别称得每棵树所产樱桃的质量如下表:
序 号 1 2 3 4 5 6 7 8 9 10
质量(千克) 14 21 27 17 18 20 19 23 19 22
据调查,市场上今年樱桃的批发价格为每千克15元.用所学的统计知识估计今年此果园樱桃的总产量与按批发价格销售樱桃所得的总收入分别为( ) A、200千克,3000元 B、1900千克,28500元C、2000千克,30000元D、1850千克,27750元
8. 1班班长统计去年1~8月“书香校园”活动中
全班同学的课外阅读数量(单位:本),绘制了
如图折线统计图,下列说法正确的是( )
(A)极差是47 (B)众数是42
(C)中位数是58
(D)每月阅读数量超过40的有4个月
9. 某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数 C.平均数 D. 极差
10. 学校商店在一段时间内销售了四种饮料共100瓶,各种饮料的销售量如下表:
品牌 甲 乙 丙 丁
销售量(瓶) 12 32 13 43
建议学校商店进货数量最多的品牌是( )
(A)甲品牌 (B)乙品牌 (C)丙品牌 (D)丁品牌
二、填空题(每空3分,共27分)
11.甲、乙两同学参加跳远训练,在相同条件下各跳了6次,统计两人的成绩得;平均数x甲=x乙,方差S2甲<S2乙,则成绩较稳定的是 .
12.若一组数据1,2, 3,x的极差为6,则x的值是 .
13.某学生7门学科考试成绩的总分是560分,其中3门学科的总分是234分,则另外4门学科成绩的平均分是_________.
14、-个样本的方差是,则这个样本的容量为_______________,平均数为_______________
15. 某校在“爱护地球 绿化祖图”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量(单位:棵) 4 5 6 8 10
人数 30 22 25 15 8
则这100名同学平均每人植树 __________棵;若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总数是__________棵.
16、5个数据分别减去100后所得新数据为8,6,-2,3,0,则原数据的平均数为 .
17、若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则另一样本x1+2,x2+2,…,xn+2,的平均数为 ,方差为 .
三、解答题
18. (本题10分)王大伯几年前承办了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如拆线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
19. (10分)某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
班级 平均数(分) 中位数(分) 众数(分)
九(1) 85
九(2) 85 100
20. (13)某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人,投票结果统计如图一:
其次,对三名候选人进行了笔试和面试两项测试,各项成绩如下表所示:
测试项目 测试成绩/分
甲 乙 丙
笔试 92 90 95
面试 85 95 80
图二是某同学根据上表绘制的一个不完整的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
28
30
32
36
34
1
2
3
4
5
日期/日
用水量/吨
·
·
·
·
·
0
某班学生1~8月课外阅读数量
折线统计图
(第8题)
70
75
80
85
90
95
100
分数
甲
乙
丙
竞选人
笔试
面试
图二
图一
姓名:_________ 得分:_______
一、选择题:(每题4分,共40分)
月用水量(吨) 5 6 7
户数 2 6 2
1. 2011年春某市发生了严重干旱,市政府号召居民节约用水,为了解居民用水情况,某小区随机抽查了10户家庭的月用水量,结果如下表:则关于这10户家庭的月用水量,下列说法错误的是( )
A.众数是6 B.极差是2
C.平均数是6 D.方差是4
2、学校快餐店有2元,3元,4元三种价格的饭菜供师生选择(每人限购一份).如图是某月的销售情况统计图,则该校师生购买饭菜费用的平均数和众数是( )
A.2.95元,3元 B.3元,3元 C.3元,4元 D.2.95元,4元
3、如图,某路口统计的某个时段来往汽车的车速(单位:千米/小时)情况,据统计图,这组车速数据的众数和中位数分别是( )
A、60千米/小时,60千米/小时 B、58千米/小时,60千米/小时
C、60千米/小时,58千米/小时 D、58千米/小时,58千米/小时
4. 某住宅小区六月份1日至5日每天用水量变化情况如图所示,那么这5天的用水量
的中位数是( )A.30吨 B.31吨 C.32吨 D.33吨
第2题 第3题 第4题
5、以下说法中正确的是( )
A.极差较大的一组数据方差也大. B.分别用一组数据中的每一个减去平均数,再将所得的差相加,若和为零,则方差为零C.在一组数据中去掉一个等于平均数的数,这组数据的方差不变. D.如果一组数据的方差等于零,则这组数据中的每一个彼此相等
6.如果一组数据,,…,的方差是2,那么一组新数据2,2,…,2的方差是( ) A. 2 B. 4 C. 8 D. 16
7、李大伯承包了一个果园,种植了100棵樱桃树,今年已进入收获期.收获时,从中任选并采摘了10棵树的樱桃,分别称得每棵树所产樱桃的质量如下表:
序 号 1 2 3 4 5 6 7 8 9 10
质量(千克) 14 21 27 17 18 20 19 23 19 22
据调查,市场上今年樱桃的批发价格为每千克15元.用所学的统计知识估计今年此果园樱桃的总产量与按批发价格销售樱桃所得的总收入分别为( ) A、200千克,3000元 B、1900千克,28500元C、2000千克,30000元D、1850千克,27750元
8. 1班班长统计去年1~8月“书香校园”活动中
全班同学的课外阅读数量(单位:本),绘制了
如图折线统计图,下列说法正确的是( )
(A)极差是47 (B)众数是42
(C)中位数是58
(D)每月阅读数量超过40的有4个月
9. 某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数 C.平均数 D. 极差
10. 学校商店在一段时间内销售了四种饮料共100瓶,各种饮料的销售量如下表:
品牌 甲 乙 丙 丁
销售量(瓶) 12 32 13 43
建议学校商店进货数量最多的品牌是( )
(A)甲品牌 (B)乙品牌 (C)丙品牌 (D)丁品牌
二、填空题(每空3分,共27分)
11.甲、乙两同学参加跳远训练,在相同条件下各跳了6次,统计两人的成绩得;平均数x甲=x乙,方差S2甲<S2乙,则成绩较稳定的是 .
12.若一组数据1,2, 3,x的极差为6,则x的值是 .
13.某学生7门学科考试成绩的总分是560分,其中3门学科的总分是234分,则另外4门学科成绩的平均分是_________.
14、-个样本的方差是,则这个样本的容量为_______________,平均数为_______________
15. 某校在“爱护地球 绿化祖图”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
植树数量(单位:棵) 4 5 6 8 10
人数 30 22 25 15 8
则这100名同学平均每人植树 __________棵;若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总数是__________棵.
16、5个数据分别减去100后所得新数据为8,6,-2,3,0,则原数据的平均数为 .
17、若样本x1+1,x2+1,…,xn+1的平均数为10,方差为2,则另一样本x1+2,x2+2,…,xn+2,的平均数为 ,方差为 .
三、解答题
18. (本题10分)王大伯几年前承办了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如拆线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
19. (10分)某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
班级 平均数(分) 中位数(分) 众数(分)
九(1) 85
九(2) 85 100
20. (13)某初中学校欲向高一级学校推荐一名学生,根据规定的推荐程序:首先由本年级200名学生民主投票,每人只能推荐一人(不设弃权票),选出了票数最多的甲、乙、丙三人,投票结果统计如图一:
其次,对三名候选人进行了笔试和面试两项测试,各项成绩如下表所示:
测试项目 测试成绩/分
甲 乙 丙
笔试 92 90 95
面试 85 95 80
图二是某同学根据上表绘制的一个不完整的条形图.
请你根据以上信息解答下列问题:
(1)补全图一和图二;
(2)请计算每名候选人的得票数;
(3)若每名候选人得一票记1分,投票、笔试、面试三项得分按照2:5:3的比确定,计算三名候选人的平均成绩,成绩高的将被录取,应该录取谁?
28
30
32
36
34
1
2
3
4
5
日期/日
用水量/吨
·
·
·
·
·
0
某班学生1~8月课外阅读数量
折线统计图
(第8题)
70
75
80
85
90
95
100
分数
甲
乙
丙
竞选人
笔试
面试
图二
图一
