山东省济南市钢城区2019-2020学年下学期八年级期末数学试卷(word版含答案)
文档属性
| 名称 | 山东省济南市钢城区2019-2020学年下学期八年级期末数学试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 116.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 11:39:47 | ||
图片预览



文档简介
2019-2020学年山东省济南市钢城区八年级(下)期末数学试卷
一、单选题(本题共计12小题,总分36分)
1.若m>n,则下列各式中不成立的是( )
A.m+3>n+3 B.﹣3m<﹣3n C.> D.m2>n2
2.下列事件为必然事件的是( )
A.打开电视机,正在播放新闻
B.任意画一个三角形,其内角和是180°
C.买一张电影票,座位号是奇数号
D.掷一枚质地均匀的硬币,正面朝上
3.如图,直线l1∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( )
A.65° B.55° C.45° D.35°
4.已知直线y=kx﹣2经过点(3,0),则关于x的不等式kx﹣2>0的解集是( )
A.x<﹣2 B.x<3 C.x>3 D.x>﹣2
5.等腰三角形一腰上的高与另一腰的夹角为40°,则它的底角的度数是( )
A.50° B.65° C.25° D.65°或25°
6.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC
7.如图,在3×3的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
A. B. C. D.
8.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
9.小强同学从﹣1,0,1,2,3,4这六个数中任选一个数,满足不等式x+1<2的概率是( )
A. B. C. D.
10.我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A. B.
C. D.
11.若关于x的不等式组的解集是x>a,则a的取值范围是( )
A.a<2 B.a≤2 C.a>2 D.a≥2
12.如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC交AC的延长线于点N,连接BD、CD.以下结论:①BM=CN;②∠DBC=∠DAN;③∠BAC+∠BDC=180°;④点D到△ABC各顶点的距离相等.正确的是( )
A.①②④ B.②③④ C.①②③ D.①③④
二、填空题(本题共计5小题,总分20分)
13.(4分)判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举一个反例.反例中的n可以是 .
14.(4分)不等式3(x﹣1)≤5﹣x的非负整数解有 个.
15.(4分)在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数是 .
16.(4分)已知直线l1:y=﹣3x+b与直线l2:y=﹣kx+1在同一坐标系的图象交于点(1,﹣b),那么方程组的解是 .
17.(4分)如图,△ABC是等腰直角三角形,AD⊥BC于点D,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=时,则线段AM的长是 .
三、解答题(本题共计7小题,总分64分)
18.(6分)解不等式,并把它的解集表示在数轴上.
19.(8分)解方程组.
20.(9分)若关于x、y的二元一次方程组的解满足x+y≤0,求m的取值范围.
21.(9分)如图,在四边形ABCD中,AD∥BC,连接BD,点E在BC边上,点F在DC边上,且∠1=∠2.
(1)求证:EF∥BD;
(2)若DB平分∠ABC,∠A=130°,∠C=70°,求∠CFE的度数.
22.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
23.(10分)某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案?
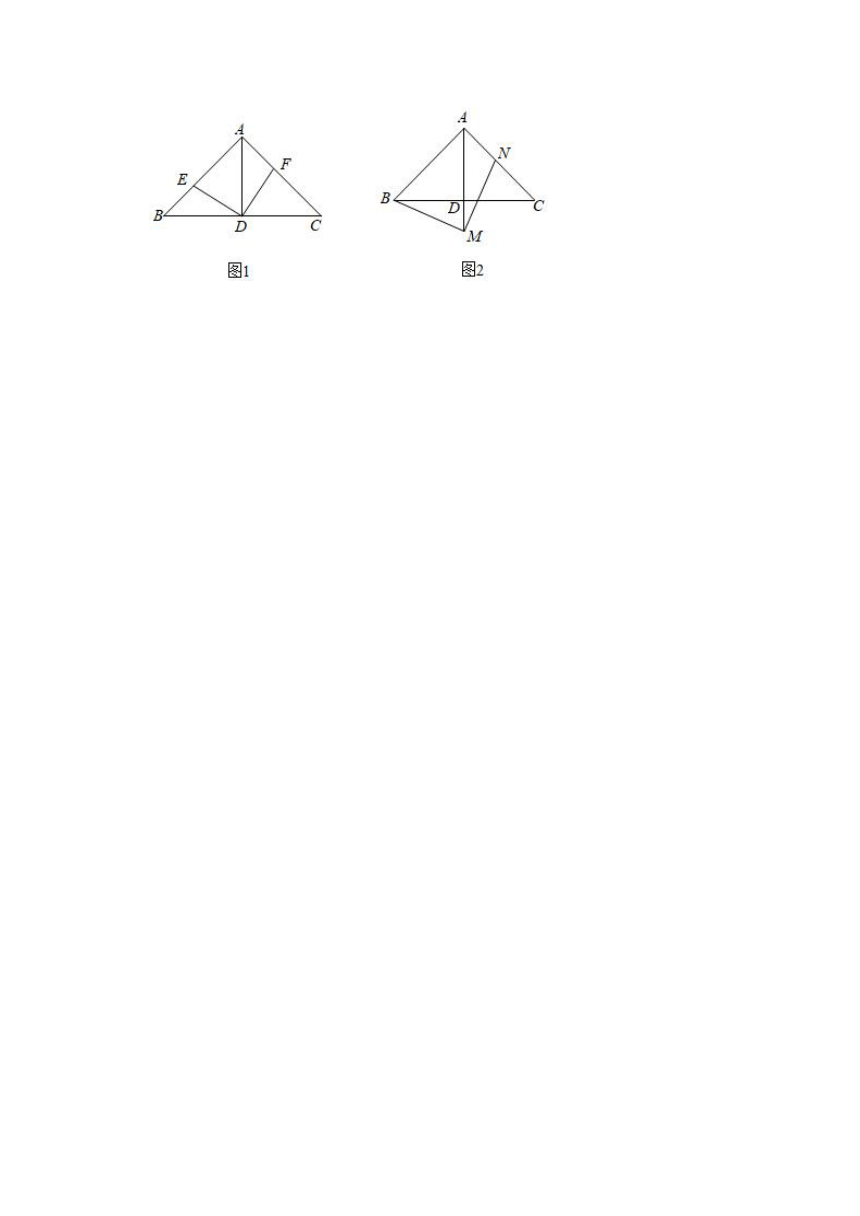
24.(12分)在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;
(2)如图2,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=AM.
参考答案
一、单选题(本题共计12小题,总分36分)
1. D.
2. B.
3. B.
4. C.
5.65°或者25°.
6. A.
7. D.
8. A.
9. C.
10. A.
11. D.
12. C.
二、填空题(本题共计5小题,总分20分)
13.﹣2(答案不唯一).
14. 3.
15. 22.
16. .
17. .
三、解答题(本题共计7小题,总分64分)
18.
解:去分母,得:2(x﹣1)﹣3x<﹣6,
去括号,得:2x﹣2﹣3x<﹣6,
移项,得:2x﹣3x<﹣6+2,
合并同类项,得:﹣x<﹣4,
系数化为1,得:x>4,
将解集表示在数轴上如下:
.
19.
解:①×2+②,得
5x=10,解得x=2.
将x=2代入①中,得
y=.
所以原方程组的解为
20.
解:将两个方程相加即可得2x+2y=4m+8,
则x+y=2m+4,
根据题意,得:2m+4≤0,
解得m≤﹣2.
21.
解:(1)如图,
∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2,
∴∠3=∠2(等量代换).
∴EF∥BD(同位角相等,两直线平行).
(2)解:∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵DB平分∠ABC(已知),
∴∠3=∠ABC=25°.
∴∠2=∠3=25°.
∵在△CFE中,∠CFE+∠2+∠C=180°(三角形内角和定理),∠C=70°,
∴∠CFE=85°.
22.
解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.
23.
解:(1)设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,
根据题意得40x+30(20﹣x)=650,
解得x=5,
则20﹣x=15,
答:甲种奖品购买了5件,乙种奖品购买了15件;
(2)设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,
根据题意得,解得≤x≤8,
∵x为整数,
∴x=7或x=8,
当x=7时,20﹣x=13;当x=8时,20﹣x=12;
答:该公司有2种不同的购买方案:甲种奖品购买了7件,乙种奖品购买了13件或甲种奖品购买了8件,乙种奖品购买了12件.
24.
解:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵AD⊥BC,
∴BD=CD,∠ADB=90°,∠BAD=∠CAD=45°,
∴∠CAD=∠B,AD=BD,
∵∠EDF=∠ADB=90°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
,
∴△BDE≌△ADF(ASA),
∴BE=AF;
(2)如图,过点M作MP⊥AM,交AB的延长线于点P,
∴∠AMP=90°,
∵∠PAM=45°,
∴∠P=∠PAM=45°,
∴AM=PM,
∵∠BMN=∠AMP=90°,
∴∠BMP=∠AMN,
∵∠DAC=∠P=45°,
在△AMN与△PMB中,
,
∴△AMN≌△PMB(ASA),
∴AN=PB,
∴AP=AB+BP=AB+AN,
在Rt△AMP中,∠AMP=90°,AM=MP,
∴AP=AM,
∴AB+AN=AM.
一、单选题(本题共计12小题,总分36分)
1.若m>n,则下列各式中不成立的是( )
A.m+3>n+3 B.﹣3m<﹣3n C.> D.m2>n2
2.下列事件为必然事件的是( )
A.打开电视机,正在播放新闻
B.任意画一个三角形,其内角和是180°
C.买一张电影票,座位号是奇数号
D.掷一枚质地均匀的硬币,正面朝上
3.如图,直线l1∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( )
A.65° B.55° C.45° D.35°
4.已知直线y=kx﹣2经过点(3,0),则关于x的不等式kx﹣2>0的解集是( )
A.x<﹣2 B.x<3 C.x>3 D.x>﹣2
5.等腰三角形一腰上的高与另一腰的夹角为40°,则它的底角的度数是( )
A.50° B.65° C.25° D.65°或25°
6.如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC
7.如图,在3×3的正方形网格中,有三个小正方形已经涂成灰色,若再任意涂灰1个白色的小正方形(每个白色的小正方形被涂成灰色的可能性相同),使新构成灰色部分的图形是轴对称图形的概率是( )
A. B. C. D.
8.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
9.小强同学从﹣1,0,1,2,3,4这六个数中任选一个数,满足不等式x+1<2的概率是( )
A. B. C. D.
10.我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )
A. B.
C. D.
11.若关于x的不等式组的解集是x>a,则a的取值范围是( )
A.a<2 B.a≤2 C.a>2 D.a≥2
12.如图,在△ABC中,∠CAB的平分线AD与BC的垂直平分线DE交于点D,DM⊥AB于点M,DN⊥AC交AC的延长线于点N,连接BD、CD.以下结论:①BM=CN;②∠DBC=∠DAN;③∠BAC+∠BDC=180°;④点D到△ABC各顶点的距离相等.正确的是( )
A.①②④ B.②③④ C.①②③ D.①③④
二、填空题(本题共计5小题,总分20分)
13.(4分)判断命题“如果n<1,那么n2﹣1<0”是假命题,只需举一个反例.反例中的n可以是 .
14.(4分)不等式3(x﹣1)≤5﹣x的非负整数解有 个.
15.(4分)在一个不透明的口袋中,装有一些除颜色外完全相同的红、白、黑三种颜色的小球.已知袋中有红球5个,白球23个,且从袋中随机摸出一个红球的概率是,则袋中黑球的个数是 .
16.(4分)已知直线l1:y=﹣3x+b与直线l2:y=﹣kx+1在同一坐标系的图象交于点(1,﹣b),那么方程组的解是 .
17.(4分)如图,△ABC是等腰直角三角形,AD⊥BC于点D,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=时,则线段AM的长是 .
三、解答题(本题共计7小题,总分64分)
18.(6分)解不等式,并把它的解集表示在数轴上.
19.(8分)解方程组.
20.(9分)若关于x、y的二元一次方程组的解满足x+y≤0,求m的取值范围.
21.(9分)如图,在四边形ABCD中,AD∥BC,连接BD,点E在BC边上,点F在DC边上,且∠1=∠2.
(1)求证:EF∥BD;
(2)若DB平分∠ABC,∠A=130°,∠C=70°,求∠CFE的度数.
22.(10分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
23.(10分)某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件.其中甲种奖品每件40元,乙种奖品每件30元
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件?
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案?
24.(12分)在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;
(2)如图2,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=AM.
参考答案
一、单选题(本题共计12小题,总分36分)
1. D.
2. B.
3. B.
4. C.
5.65°或者25°.
6. A.
7. D.
8. A.
9. C.
10. A.
11. D.
12. C.
二、填空题(本题共计5小题,总分20分)
13.﹣2(答案不唯一).
14. 3.
15. 22.
16. .
17. .
三、解答题(本题共计7小题,总分64分)
18.
解:去分母,得:2(x﹣1)﹣3x<﹣6,
去括号,得:2x﹣2﹣3x<﹣6,
移项,得:2x﹣3x<﹣6+2,
合并同类项,得:﹣x<﹣4,
系数化为1,得:x>4,
将解集表示在数轴上如下:
.
19.
解:①×2+②,得
5x=10,解得x=2.
将x=2代入①中,得
y=.
所以原方程组的解为
20.
解:将两个方程相加即可得2x+2y=4m+8,
则x+y=2m+4,
根据题意,得:2m+4≤0,
解得m≤﹣2.
21.
解:(1)如图,
∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2,
∴∠3=∠2(等量代换).
∴EF∥BD(同位角相等,两直线平行).
(2)解:∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵DB平分∠ABC(已知),
∴∠3=∠ABC=25°.
∴∠2=∠3=25°.
∵在△CFE中,∠CFE+∠2+∠C=180°(三角形内角和定理),∠C=70°,
∴∠CFE=85°.
22.
解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°,
∴∠BDE=∠C=69°.
23.
解:(1)设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,
根据题意得40x+30(20﹣x)=650,
解得x=5,
则20﹣x=15,
答:甲种奖品购买了5件,乙种奖品购买了15件;
(2)设甲种奖品购买了x件,乙种奖品购买了(20﹣x)件,
根据题意得,解得≤x≤8,
∵x为整数,
∴x=7或x=8,
当x=7时,20﹣x=13;当x=8时,20﹣x=12;
答:该公司有2种不同的购买方案:甲种奖品购买了7件,乙种奖品购买了13件或甲种奖品购买了8件,乙种奖品购买了12件.
24.
解:(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵AD⊥BC,
∴BD=CD,∠ADB=90°,∠BAD=∠CAD=45°,
∴∠CAD=∠B,AD=BD,
∵∠EDF=∠ADB=90°,
∴∠BDE=∠ADF,
在△BDE与△ADF中,
,
∴△BDE≌△ADF(ASA),
∴BE=AF;
(2)如图,过点M作MP⊥AM,交AB的延长线于点P,
∴∠AMP=90°,
∵∠PAM=45°,
∴∠P=∠PAM=45°,
∴AM=PM,
∵∠BMN=∠AMP=90°,
∴∠BMP=∠AMN,
∵∠DAC=∠P=45°,
在△AMN与△PMB中,
,
∴△AMN≌△PMB(ASA),
∴AN=PB,
∴AP=AB+BP=AB+AN,
在Rt△AMP中,∠AMP=90°,AM=MP,
∴AP=AM,
∴AB+AN=AM.
同课章节目录
