华东师大版七上数学 2.8.1加减法统一成加法 课件(含2课时,共33张PPT)
文档属性
| 名称 | 华东师大版七上数学 2.8.1加减法统一成加法 课件(含2课时,共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 717.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 11:07:40 | ||
图片预览











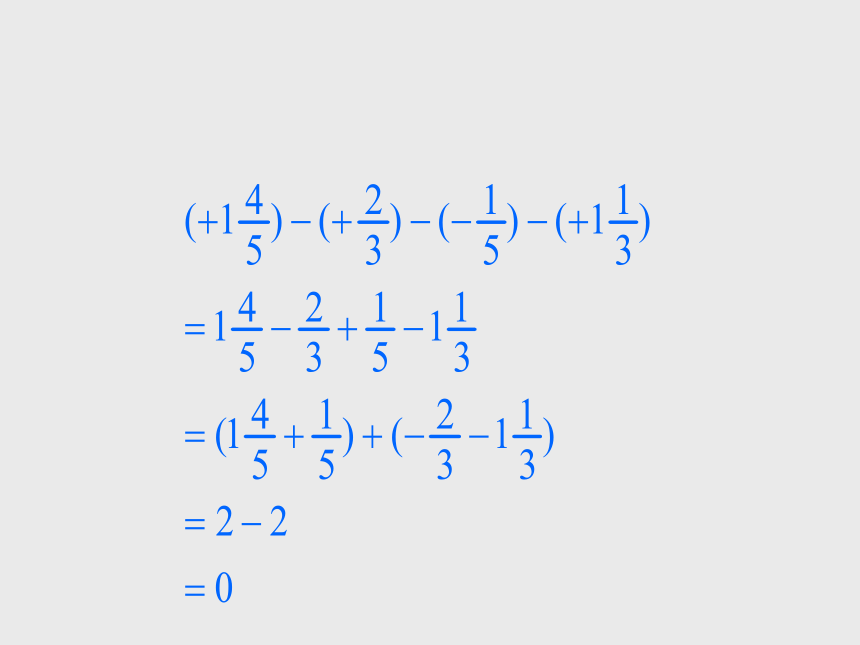
文档简介
(共33张PPT)
(第一课时)
教学目标
知识与能力要求:经历探索有理数加减混合运算的过程,理解省略加号的代数和的式子的意义。
解决问题:初步学会从数学的角度来理解问题,并能进行包括小数和分数在类的的有理数加法运算。
情感态度与价值观:体验数学符号和式子是有效表达和描述现实世界的重要手段,认识数学是解决实际问题的重要工具,进一步提高学生学习数学运算的热情。
教学重点、难点
将有理数加减混合运算分两步化成省略加号的代数和的形 式,并熟练进行有理数加减混合运算。
一、温故知新、引入课题
前面我们学习了有理数的加法和减法,同学们学得都很好!请同学们看以下题目:
- 8-(-10);(-6)-(+4).
(1)读出这两个算式.
(2)“+、-”读作什么?是哪种符号?
(3) “+、-”又读作什么?是什么符号
(4)这两个题目运算结果是多少?
(5)你根据什么运算法则计算的?
由此可得:减法往往通过转化成加法后来运算.
对于多个数的加减都可统一成加法
(-8)-(-10)+(-6)-(+4)可写成:
(-8)+(+10)+(-6)+(-4)
先利用减法法则统一成加法,再将各个加数的括号和它前面的加号省略不写,得:-8 + 10 - 6 - 4
看作和式,读作: “负8、正10、负6、负4的和”,按运算意义可读作:“负8加10减6减4”。
二、 得出法则,揭示内涵
例1 将下列式子先统一成加法,再写成省略加号和括号的和的形式,并把它读出来。
1.(-40)-(+27)+19-24-(-32)
2. -9-(-2)+(-3)-4
三、例题示范,初步运用
解:1 (-40)-(+27)+19-24-(-32)
=(-40) + (- 27)+19+( - 24)+ (+32)
=-40-27+19-24+32
2 -9-(-2)+(-3)-4
= -9 +(+ 2)+(-3) + (-4 )
=-9 + 2 - 3-4
我们把它读出来
规律:同号得“+”,异号得“-”
由此你发现了什么规律?
将下列式子先统一成加法,再写成省略加号和括号的和的形式,并把它读出来。
1.(-4 )-(+7 )+( - 9 )-(-3 )
2. ( + 2.3 )-(-2.1)+(-3.2 )-4
1.-4-7-9+3
读作:负4减7减9加3 或-4、-7、-9、3的和
2.2.3+2.1-3.2-4
读作:2.3加2.1减3.2减4或2.3、2.1、-3.2、-4的和
我们把它读出来
例2 把
写成省略加号的和的形式,并把它读出来
解:
你会去读吗?试一试
1、把(-6) -(-4) +(+2) -(+3) 写成省略括号的和的形式,正确的是( )
A、-6-4+2+3 B、-6-4+2-3
C、-6+4+2-3 D、6+4+2-3
2、判断下面是否正确,并说明理由。
1)5-3=3-5
2)5-3=-35
3)5-3+2=(5-3)+2=5-(3+2)
C
(错,交换时,应该连同符号一起交换)
(错,交换后,应该是5-3=-3+5 )
错,结合后,应该是5-3+2=(5-3)+2=5+(-3+2)
四、分层练习,形成能力
3、请你概括有理数加减混合运算步骤及应该注意的问题。
步骤:
第一步、运用减法法则把减法转化成加法。
第二步、写成省略加号和括号的代数和的形式。
第三步、应用加法运算律和加法法则进行计算。
注意:
1、应用加法交换、结合律时,要连同前面的符号一起交换。
2、应用运算律进行计算的原则:
①互为相反数的结合,②和为整数的结合,③同分母或容易通分的结合,④符号相同的结合,⑤带分数先化成假分数或把它分离成整数和分数再结合。
4、请阅读理解下面题目的解答过程,再回答问题。
…第一步
…第二步
…第三步
…第四步
…第五步
回答:1、上述解答第 步开始出现错误。
2、得到第一步的理由是 。
3、从第一步到第二步使用了哪些运算律?
4、请写出正确的解答过程。
二
减法法则
加法交换律、结合律
判断题:对的在括号里打“√”,错的在括号里打“×”,并举出反例.
(1)若a,b同号,则a+b=|a|+|b|.( )
(2)若a,b异号,则a+b=|a|-|b|.( )
(3)若a<0、b<0,则a+b=-(|a|+|b|).( )
(4)若a,b异号,则|a-b|=|a|+|b|.( )
(5)若a+b=0,则|a|=|b|.( )
×
×
∨
∨
∨
六、课堂小结,突出重点
1、有理数加减混合运算 的步骤
第一步、运用减法法则把减法转化成加法。
第二步、写成省略加号和括号的代数和的形式。
第三步、应用加法运算律和加法法则进行计算。
如果括号内不止一个数时,先计算小括号,再中括号,最后大括号;有绝对值时,先计算绝对值。
2、应用运算律进行计算的原则:
①互为相反数的结合;
②和为整数的结合;
③同分母或容易通分的结合;
④符号相同的结合;
⑤带分数先化成假分数或把它分离成整数和分数再结合。
本节课里我的收获是……
第二课时
熟练地进行有理数的加减混合运算及其运算顺序。
能灵活运用加法运算简化运算
一、温故知新、引入课题
复习提问:
(1)有理数的加法法则,减法法则分别是怎样的
(2)有理数的减法法则,告诉我们什么?
你记牢了吗?说说看
有理数的加法法则,减法法则分别是怎样的
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得零;
(4)一个数与零相加,仍得这个数;
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
1.算式2-3-8+7有哪几个有理数的代数和
2.是否所有含有有理数加减混合运算的式子都能化成有理数的代数和?
3.有理数加法运算,满足哪几条运算律?
4.如何计算-3+5-9+3+10+2-1比较简便?
-3+5-9+3+10+2-1
=(-3+3)+〔(-1-9)+10〕+5+2
=0+0+5+2=7
由于算式可理解为-3,5,-9,3,10,2,-1等七个数的和,因此应用加法结合律、交换律,这七个数可随意结合、交换进行运算,使运算简便。
因为有理数的加减法可以统一成加法,所以在进行有理数加减混合运算时,可以适当应用加大运算律,使计算简便
二、 得出法则,揭示内涵
三 例题示范,初步运用
例1:计算
(1)-24+3.2-16-3.5+0.3
解: -24+3.2-16-3.5+0.3
=( -24-16)+( 3.2+0.3)-3.5
= -40+(3.5-3.5)
= -40+0=-40
你发现此题的解题
技巧了吗?说说看
解题小技巧:运用运算律将正负数分别相加。
解:
解题小技巧:在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数
你发现此题的解题
技巧了吗?说说看
(3)(-0.5)-(-0.125)+(+2.75)-(+5.5)
解:(-0.5)-(-1/4)+(+2.75)-(+5.5)
=(-0.5)+(+0.25)+(+2.75)+(-5.5)
=-0.5+0.25+2.75-5.5
=(-0.5-5.5)+(0.25+2.75)
=-6+3=-3
你发现此题的解题
技巧了吗?说说看
解题小技巧:在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数
有理数加减混合运算步骤:
第一步:写成省略加号的形式;
第二步:运用加法交换律,交换加法的位置;
第三步:适当运用加法结合律进行运算。
注意:
在有理数加减混合运算过程中,要强调:
在交换加数位置时,要连同加数前面的符号一起交换。
由以上的解题有理数的加减运算一般的步骤是什么?请总结:
比如: (-5)+( -8) - (+6)= -5 - 8 -6= - 19
再比如: ( -5)+ (-8)+(+6)= -5 -8 +6= -13+6= - 7
练一练:某水利勘察队,第一天向上游走 6.8 千米,第二天又
向上游走8.3 千米,第三天向下游走2.8千米,第四天又向下
游走5.3千米,用有理数加法计算此时勘察队在出发点的哪个
方向 相距多少千米
四、分层练习,形成能力
2.计算:
(1)10-24-15+26-24+18-20 (2)(+0.5)-1/3+(-1/4)-(+1/6) (3)14-28-32-16+18+32
(1)10-24-15+26-24+18-20
解: 10-24-15+26-24+18-20
=(10+26+18)+(-24-15-24-20)
=54-83
=-29
(2)(+0.5)-1/3+(-1/4)-(+1/6)
解: (+0.5)-1/3+(-1/4)-(+1/6)
=(+1/2)+( -1/3)+(-1/4)+(-1/6)
=1/2-1/3-1/4-1/6
=(1/2-1/4)+(-1/3-1/6)
=1/4-1/2
=-1/4
(3)14-28-32-16+18+32
解:
原式
=(14+18)+(32-32)+(-28-16)
=32+0-44
=-12
以上各题你做对了吗?
某公路养护小组乘车沿南北公路巡护维护。某天早晨从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米): +18,-9,-7,-14,-6,+13,-6,-8,B地A地何方?相距多少千米?若汽车行驶每千米耗油a升,求该天共耗油多少升?
解:(+18)+(-9)+(-7)+(-14)+(-6)+(+13)+(-6)+(-8)=-5(千米)
所以,B地在A地的南方,距A地5千米处。
|+18|+|-9|+|-7|+|-14|+|-6|+|+13|+|-6|+|-8|=81(千米)
81X a=81 a
答:A地在B地的南方距B地5千米。求该天共耗油81 a升
(分析)将行驶记录相加,若结果为正,则在原出发地A地的正北方向;若结果为负,则在原出发地A地的正南方向。汽车耗油跟方向无关,只跟行驶的总路程有关。而每段路程即记录的绝对值,总路程即每段路程绝对值的和。
有理数运算技巧总结:
(1)运用运算律将正负数分别相加。
(2)分母相同或有倍数关系的分数结合相加。
(3)在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数。
(4)互为相反数的两数可先相加。
(5)带分数整数部分,小数部分可拆开相加。
本节课里我的收获是……
(第一课时)
教学目标
知识与能力要求:经历探索有理数加减混合运算的过程,理解省略加号的代数和的式子的意义。
解决问题:初步学会从数学的角度来理解问题,并能进行包括小数和分数在类的的有理数加法运算。
情感态度与价值观:体验数学符号和式子是有效表达和描述现实世界的重要手段,认识数学是解决实际问题的重要工具,进一步提高学生学习数学运算的热情。
教学重点、难点
将有理数加减混合运算分两步化成省略加号的代数和的形 式,并熟练进行有理数加减混合运算。
一、温故知新、引入课题
前面我们学习了有理数的加法和减法,同学们学得都很好!请同学们看以下题目:
- 8-(-10);(-6)-(+4).
(1)读出这两个算式.
(2)“+、-”读作什么?是哪种符号?
(3) “+、-”又读作什么?是什么符号
(4)这两个题目运算结果是多少?
(5)你根据什么运算法则计算的?
由此可得:减法往往通过转化成加法后来运算.
对于多个数的加减都可统一成加法
(-8)-(-10)+(-6)-(+4)可写成:
(-8)+(+10)+(-6)+(-4)
先利用减法法则统一成加法,再将各个加数的括号和它前面的加号省略不写,得:-8 + 10 - 6 - 4
看作和式,读作: “负8、正10、负6、负4的和”,按运算意义可读作:“负8加10减6减4”。
二、 得出法则,揭示内涵
例1 将下列式子先统一成加法,再写成省略加号和括号的和的形式,并把它读出来。
1.(-40)-(+27)+19-24-(-32)
2. -9-(-2)+(-3)-4
三、例题示范,初步运用
解:1 (-40)-(+27)+19-24-(-32)
=(-40) + (- 27)+19+( - 24)+ (+32)
=-40-27+19-24+32
2 -9-(-2)+(-3)-4
= -9 +(+ 2)+(-3) + (-4 )
=-9 + 2 - 3-4
我们把它读出来
规律:同号得“+”,异号得“-”
由此你发现了什么规律?
将下列式子先统一成加法,再写成省略加号和括号的和的形式,并把它读出来。
1.(-4 )-(+7 )+( - 9 )-(-3 )
2. ( + 2.3 )-(-2.1)+(-3.2 )-4
1.-4-7-9+3
读作:负4减7减9加3 或-4、-7、-9、3的和
2.2.3+2.1-3.2-4
读作:2.3加2.1减3.2减4或2.3、2.1、-3.2、-4的和
我们把它读出来
例2 把
写成省略加号的和的形式,并把它读出来
解:
你会去读吗?试一试
1、把(-6) -(-4) +(+2) -(+3) 写成省略括号的和的形式,正确的是( )
A、-6-4+2+3 B、-6-4+2-3
C、-6+4+2-3 D、6+4+2-3
2、判断下面是否正确,并说明理由。
1)5-3=3-5
2)5-3=-35
3)5-3+2=(5-3)+2=5-(3+2)
C
(错,交换时,应该连同符号一起交换)
(错,交换后,应该是5-3=-3+5 )
错,结合后,应该是5-3+2=(5-3)+2=5+(-3+2)
四、分层练习,形成能力
3、请你概括有理数加减混合运算步骤及应该注意的问题。
步骤:
第一步、运用减法法则把减法转化成加法。
第二步、写成省略加号和括号的代数和的形式。
第三步、应用加法运算律和加法法则进行计算。
注意:
1、应用加法交换、结合律时,要连同前面的符号一起交换。
2、应用运算律进行计算的原则:
①互为相反数的结合,②和为整数的结合,③同分母或容易通分的结合,④符号相同的结合,⑤带分数先化成假分数或把它分离成整数和分数再结合。
4、请阅读理解下面题目的解答过程,再回答问题。
…第一步
…第二步
…第三步
…第四步
…第五步
回答:1、上述解答第 步开始出现错误。
2、得到第一步的理由是 。
3、从第一步到第二步使用了哪些运算律?
4、请写出正确的解答过程。
二
减法法则
加法交换律、结合律
判断题:对的在括号里打“√”,错的在括号里打“×”,并举出反例.
(1)若a,b同号,则a+b=|a|+|b|.( )
(2)若a,b异号,则a+b=|a|-|b|.( )
(3)若a<0、b<0,则a+b=-(|a|+|b|).( )
(4)若a,b异号,则|a-b|=|a|+|b|.( )
(5)若a+b=0,则|a|=|b|.( )
×
×
∨
∨
∨
六、课堂小结,突出重点
1、有理数加减混合运算 的步骤
第一步、运用减法法则把减法转化成加法。
第二步、写成省略加号和括号的代数和的形式。
第三步、应用加法运算律和加法法则进行计算。
如果括号内不止一个数时,先计算小括号,再中括号,最后大括号;有绝对值时,先计算绝对值。
2、应用运算律进行计算的原则:
①互为相反数的结合;
②和为整数的结合;
③同分母或容易通分的结合;
④符号相同的结合;
⑤带分数先化成假分数或把它分离成整数和分数再结合。
本节课里我的收获是……
第二课时
熟练地进行有理数的加减混合运算及其运算顺序。
能灵活运用加法运算简化运算
一、温故知新、引入课题
复习提问:
(1)有理数的加法法则,减法法则分别是怎样的
(2)有理数的减法法则,告诉我们什么?
你记牢了吗?说说看
有理数的加法法则,减法法则分别是怎样的
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;
(3)互为相反数的两个数相加得零;
(4)一个数与零相加,仍得这个数;
有理数的减法法则:
减去一个数,等于加上这个数的相反数.
1.算式2-3-8+7有哪几个有理数的代数和
2.是否所有含有有理数加减混合运算的式子都能化成有理数的代数和?
3.有理数加法运算,满足哪几条运算律?
4.如何计算-3+5-9+3+10+2-1比较简便?
-3+5-9+3+10+2-1
=(-3+3)+〔(-1-9)+10〕+5+2
=0+0+5+2=7
由于算式可理解为-3,5,-9,3,10,2,-1等七个数的和,因此应用加法结合律、交换律,这七个数可随意结合、交换进行运算,使运算简便。
因为有理数的加减法可以统一成加法,所以在进行有理数加减混合运算时,可以适当应用加大运算律,使计算简便
二、 得出法则,揭示内涵
三 例题示范,初步运用
例1:计算
(1)-24+3.2-16-3.5+0.3
解: -24+3.2-16-3.5+0.3
=( -24-16)+( 3.2+0.3)-3.5
= -40+(3.5-3.5)
= -40+0=-40
你发现此题的解题
技巧了吗?说说看
解题小技巧:运用运算律将正负数分别相加。
解:
解题小技巧:在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数
你发现此题的解题
技巧了吗?说说看
(3)(-0.5)-(-0.125)+(+2.75)-(+5.5)
解:(-0.5)-(-1/4)+(+2.75)-(+5.5)
=(-0.5)+(+0.25)+(+2.75)+(-5.5)
=-0.5+0.25+2.75-5.5
=(-0.5-5.5)+(0.25+2.75)
=-6+3=-3
你发现此题的解题
技巧了吗?说说看
解题小技巧:在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数
有理数加减混合运算步骤:
第一步:写成省略加号的形式;
第二步:运用加法交换律,交换加法的位置;
第三步:适当运用加法结合律进行运算。
注意:
在有理数加减混合运算过程中,要强调:
在交换加数位置时,要连同加数前面的符号一起交换。
由以上的解题有理数的加减运算一般的步骤是什么?请总结:
比如: (-5)+( -8) - (+6)= -5 - 8 -6= - 19
再比如: ( -5)+ (-8)+(+6)= -5 -8 +6= -13+6= - 7
练一练:某水利勘察队,第一天向上游走 6.8 千米,第二天又
向上游走8.3 千米,第三天向下游走2.8千米,第四天又向下
游走5.3千米,用有理数加法计算此时勘察队在出发点的哪个
方向 相距多少千米
四、分层练习,形成能力
2.计算:
(1)10-24-15+26-24+18-20 (2)(+0.5)-1/3+(-1/4)-(+1/6) (3)14-28-32-16+18+32
(1)10-24-15+26-24+18-20
解: 10-24-15+26-24+18-20
=(10+26+18)+(-24-15-24-20)
=54-83
=-29
(2)(+0.5)-1/3+(-1/4)-(+1/6)
解: (+0.5)-1/3+(-1/4)-(+1/6)
=(+1/2)+( -1/3)+(-1/4)+(-1/6)
=1/2-1/3-1/4-1/6
=(1/2-1/4)+(-1/3-1/6)
=1/4-1/2
=-1/4
(3)14-28-32-16+18+32
解:
原式
=(14+18)+(32-32)+(-28-16)
=32+0-44
=-12
以上各题你做对了吗?
某公路养护小组乘车沿南北公路巡护维护。某天早晨从A地出发,晚上最后到达B地,约定向北为正方向,当天的行驶记录如下(单位:千米): +18,-9,-7,-14,-6,+13,-6,-8,B地A地何方?相距多少千米?若汽车行驶每千米耗油a升,求该天共耗油多少升?
解:(+18)+(-9)+(-7)+(-14)+(-6)+(+13)+(-6)+(-8)=-5(千米)
所以,B地在A地的南方,距A地5千米处。
|+18|+|-9|+|-7|+|-14|+|-6|+|+13|+|-6|+|-8|=81(千米)
81X a=81 a
答:A地在B地的南方距B地5千米。求该天共耗油81 a升
(分析)将行驶记录相加,若结果为正,则在原出发地A地的正北方向;若结果为负,则在原出发地A地的正南方向。汽车耗油跟方向无关,只跟行驶的总路程有关。而每段路程即记录的绝对值,总路程即每段路程绝对值的和。
有理数运算技巧总结:
(1)运用运算律将正负数分别相加。
(2)分母相同或有倍数关系的分数结合相加。
(3)在式子中若既有分数又有小数,把小数统一成分数或把分数统一成小数。
(4)互为相反数的两数可先相加。
(5)带分数整数部分,小数部分可拆开相加。
本节课里我的收获是……
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
