2020-2021学年人教版数学九年级上册21.3 实际问题与一元二次方程(24张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学九年级上册21.3 实际问题与一元二次方程(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 14:37:17 | ||
图片预览








文档简介
实际问题与
一元二次方程
活动1
问题:
通过上节课的学习,大家学到了哪些知识和方法?
活动2
要设计一本书的封面,封面长27cm ,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上下边衬等宽,左右边衬等宽,应如何设计四周边衬的宽度(精确到0.1cm)?
(课件:设计封面)
问题:
(1)本题中有哪些数量关系?
(2)如何理解“正中央是一个与整个封面
长宽比例相同的矩形”?
(3)如何利用已知的数量关系选取未知
数并列出方程?
(4)解方程并得出结论,对比几种方法
各有什么特点?
活动2
如图,某中学为方便师生活动,准备
在长30m,宽20m的矩形草坪上修筑两横
两纵四条小路,横纵路的宽度之比为3∶2 ,
若使余下的草坪面积是原来草坪面积的
四分之三,则路宽应为多少?
课件:设计图案
活动3
活动3
问题:
(1)本题中有哪些数量关系?
(2)由这些数量关系还能得到什么新
的结论?你想如何利用这些数量关系?为
什么?如何列方程?
(3)对比下列两个图形,它们有什么
联系与区别?
(4)有什么方法使本题易于解决?
活动3
利用图形的变换--平移
活动4
问题:
通过本课的学习,大家有什么新的收获和体会?
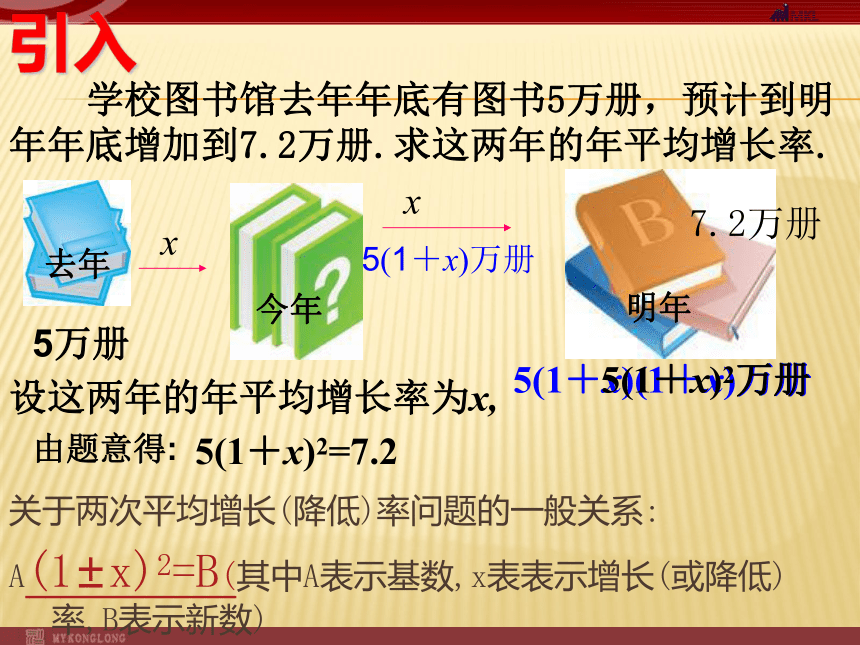
学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.
设这两年的年平均增长率为x,
去年
今年
明年
5万册
5(1+x)万册
5(1+x)(1+x)万册
x
x
由题意得:
5(1+x)2=7.2
5(1+x)2万册
7.2万册
引入
关于两次平均增长(降低)率问题的一般关系:
A(1±x)2=B(其中A表示基数,x表表示增长(或降低)率,B表示新数)
例1:琼海市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少? (精确到0.1%)
尝试探索,合作交流,解决问题
1、翻一番,你是如何理解的?
(翻一番,即为原净收入的2倍,若设原值为1,那么两年后的值就是2)
2、“平均年增长率”你是如何理解的。
(“平均年增长率”指的是每一年净收入增长的百分数是一个相同的值。即每年按同样的百分数增加,而增长的绝对数是不相同的)
3、独立思考后,小组交流,讨论。
4、展示成果,相互补充。
解:设平均年增长率应为x,依题意,得
因为增长率不能为负数
所以增长率应为
解这个方程,得
尝试探索,合作交流,解决问题
在例1中,(1)翻一番是什么意思?设原值为1,方程应该如何列?设原值为A,方程又应该如何列?
(2)若调整计划,两年后的财政净收入值为原值的1.5倍、1.2倍、…,那么两年中的平均年增长率相应地调整为多少?
又若第二年的增长率为第一年的2倍,那么第一年的增长率为多少时可以实现市财政净收入翻一番?
拓展应用
拓展应用
若调整计划,两年后的财政净收入值为原值的1.5倍、1.2倍、…,那么两年中的平均年增长率相应地调整为多少?
又若第二年的增长率为第一年的2倍,那么第一年的增长率为多少时可以实现市财政净收入翻一番?
例2:某商品经两次降价,零售价降为原来的一半,已知两次降价的百分率一样。求每次降价的百分率。(精确到0.1%)
分析:“两次降价的百分率一样”,指的是第一次和第二次降价的百分数是一个相同的值,即两次按同样的百分数减少,而减少的绝对数是不相同的,设每次降价的百分率为x,若原价为a,则第一次降价后的零售价为a-ax=a(1-x),又以这个价格为基础,再算第二次降价后的零售价。
思考:原价和现在的价格没有具体数字,如何列方程?请同学们联系已有的知识讨论、交流。
问题思考
解:设原价为1个单位,每次降价的百分率为x.根据题意,得
解这个方程,得
问题解答
由于降价的百分率不可能大于1,所以
不符合题意,因此符合本题要求的x为
≈29.3 %
答:每次降价的百分率为29.3%.
问题解答
?
1、党的十六大提出全面建设小康社会,加快推进社会主义现代化建设,力争国民生产总值到2020年比2000年翻两番,在本世纪的头二十年(2001年至2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的平均增长率为x,那么x满足的方程为_____________
小试身手
(1+x)2=4
?
?
?
2、某经济开发区今年一月份工业产值达50亿元,第一季度总产值达175亿元,问二、三月份平均每月的增长率为多少?设平均每月增长率为x,根据题意得方程:________________________
小试身手
50+50(1+x)+50(1+x) 2=175
练习1:某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,
每次降价的百分率为 x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
练习2.某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分之几?
练习3、某钢铁厂去年1月某种钢产量为5000吨,3月上升到7200吨,这两个月平均每月增长的百分率是多少?
解:设平均每月增长的百分率为x,依题意,得
解这个方程,得
因为
不合题意,所以只能取
答:平均每月增长的百分率是
小结 拓展
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,注明单位且要贴近生活.
列方程解应用题的关键是: 找出相等关系.
关于两次平均增长(降低)率问题的一般关系:
A(1±x)2=B(其中A表示基数,x表表示增长(或降低)率,B表示新数)
关于量的变化率问题,不管是增加还是减少,都是变化前的数据为基础,每次按相同的百分数变化,若原始数据为a,设平均变化率为x,经第一次变化后数据为a(1±x);经第二次变化后数据为a(1±x)2。在依题意列出方程并解得x值后,还要依据0<x<1的条件,做符合题意的解答。
小结 拓展
一元二次方程
活动1
问题:
通过上节课的学习,大家学到了哪些知识和方法?
活动2
要设计一本书的封面,封面长27cm ,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的彩色边衬所占面积是封面面积的四分之一,上下边衬等宽,左右边衬等宽,应如何设计四周边衬的宽度(精确到0.1cm)?
(课件:设计封面)
问题:
(1)本题中有哪些数量关系?
(2)如何理解“正中央是一个与整个封面
长宽比例相同的矩形”?
(3)如何利用已知的数量关系选取未知
数并列出方程?
(4)解方程并得出结论,对比几种方法
各有什么特点?
活动2
如图,某中学为方便师生活动,准备
在长30m,宽20m的矩形草坪上修筑两横
两纵四条小路,横纵路的宽度之比为3∶2 ,
若使余下的草坪面积是原来草坪面积的
四分之三,则路宽应为多少?
课件:设计图案
活动3
活动3
问题:
(1)本题中有哪些数量关系?
(2)由这些数量关系还能得到什么新
的结论?你想如何利用这些数量关系?为
什么?如何列方程?
(3)对比下列两个图形,它们有什么
联系与区别?
(4)有什么方法使本题易于解决?
活动3
利用图形的变换--平移
活动4
问题:
通过本课的学习,大家有什么新的收获和体会?
学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.
设这两年的年平均增长率为x,
去年
今年
明年
5万册
5(1+x)万册
5(1+x)(1+x)万册
x
x
由题意得:
5(1+x)2=7.2
5(1+x)2万册
7.2万册
引入
关于两次平均增长(降低)率问题的一般关系:
A(1±x)2=B(其中A表示基数,x表表示增长(或降低)率,B表示新数)
例1:琼海市市政府考虑在两年后实现市财政净收入翻一番,那么这两年中财政净收入的平均年增长率应为多少? (精确到0.1%)
尝试探索,合作交流,解决问题
1、翻一番,你是如何理解的?
(翻一番,即为原净收入的2倍,若设原值为1,那么两年后的值就是2)
2、“平均年增长率”你是如何理解的。
(“平均年增长率”指的是每一年净收入增长的百分数是一个相同的值。即每年按同样的百分数增加,而增长的绝对数是不相同的)
3、独立思考后,小组交流,讨论。
4、展示成果,相互补充。
解:设平均年增长率应为x,依题意,得
因为增长率不能为负数
所以增长率应为
解这个方程,得
尝试探索,合作交流,解决问题
在例1中,(1)翻一番是什么意思?设原值为1,方程应该如何列?设原值为A,方程又应该如何列?
(2)若调整计划,两年后的财政净收入值为原值的1.5倍、1.2倍、…,那么两年中的平均年增长率相应地调整为多少?
又若第二年的增长率为第一年的2倍,那么第一年的增长率为多少时可以实现市财政净收入翻一番?
拓展应用
拓展应用
若调整计划,两年后的财政净收入值为原值的1.5倍、1.2倍、…,那么两年中的平均年增长率相应地调整为多少?
又若第二年的增长率为第一年的2倍,那么第一年的增长率为多少时可以实现市财政净收入翻一番?
例2:某商品经两次降价,零售价降为原来的一半,已知两次降价的百分率一样。求每次降价的百分率。(精确到0.1%)
分析:“两次降价的百分率一样”,指的是第一次和第二次降价的百分数是一个相同的值,即两次按同样的百分数减少,而减少的绝对数是不相同的,设每次降价的百分率为x,若原价为a,则第一次降价后的零售价为a-ax=a(1-x),又以这个价格为基础,再算第二次降价后的零售价。
思考:原价和现在的价格没有具体数字,如何列方程?请同学们联系已有的知识讨论、交流。
问题思考
解:设原价为1个单位,每次降价的百分率为x.根据题意,得
解这个方程,得
问题解答
由于降价的百分率不可能大于1,所以
不符合题意,因此符合本题要求的x为
≈29.3 %
答:每次降价的百分率为29.3%.
问题解答
?
1、党的十六大提出全面建设小康社会,加快推进社会主义现代化建设,力争国民生产总值到2020年比2000年翻两番,在本世纪的头二十年(2001年至2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的平均增长率为x,那么x满足的方程为_____________
小试身手
(1+x)2=4
?
?
?
2、某经济开发区今年一月份工业产值达50亿元,第一季度总产值达175亿元,问二、三月份平均每月的增长率为多少?设平均每月增长率为x,根据题意得方程:________________________
小试身手
50+50(1+x)+50(1+x) 2=175
练习1:某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,
每次降价的百分率为 x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
练习2.某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分之几?
练习3、某钢铁厂去年1月某种钢产量为5000吨,3月上升到7200吨,这两个月平均每月增长的百分率是多少?
解:设平均每月增长的百分率为x,依题意,得
解这个方程,得
因为
不合题意,所以只能取
答:平均每月增长的百分率是
小结 拓展
列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,注明单位且要贴近生活.
列方程解应用题的关键是: 找出相等关系.
关于两次平均增长(降低)率问题的一般关系:
A(1±x)2=B(其中A表示基数,x表表示增长(或降低)率,B表示新数)
关于量的变化率问题,不管是增加还是减少,都是变化前的数据为基础,每次按相同的百分数变化,若原始数据为a,设平均变化率为x,经第一次变化后数据为a(1±x);经第二次变化后数据为a(1±x)2。在依题意列出方程并解得x值后,还要依据0<x<1的条件,做符合题意的解答。
小结 拓展
同课章节目录
