六年级下册数学教案-6.5 大树有多高 苏教版(表格式)
文档属性
| 名称 | 六年级下册数学教案-6.5 大树有多高 苏教版(表格式) | 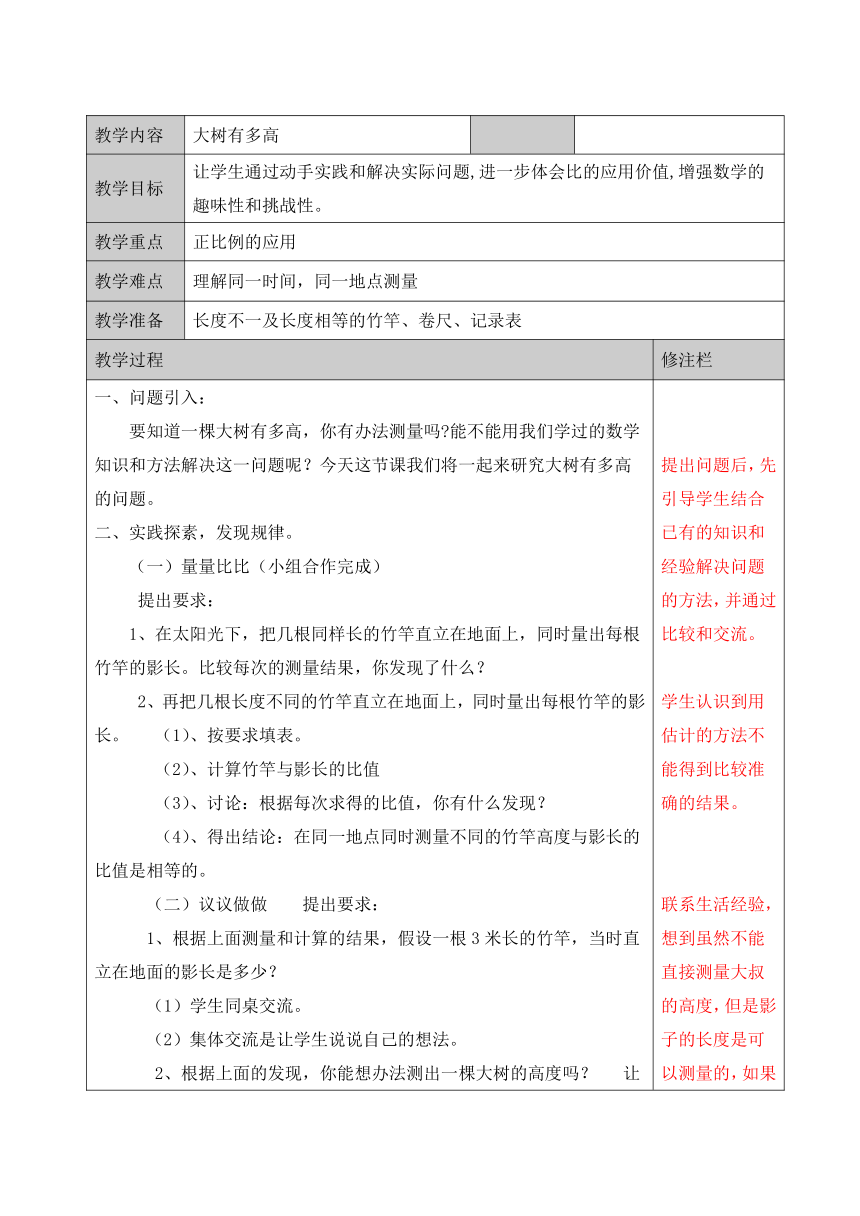 | |
| 格式 | doc | ||
| 文件大小 | 22.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 09:15:47 | ||
图片预览

文档简介
教学内容 大树有多高
教学目标 让学生通过动手实践和解决实际问题,进一步体会比的应用价值,增强数学的趣味性和挑战性。
教学重点 正比例的应用
教学难点 理解同一时间,同一地点测量
教学准备 长度不一及长度相等的竹竿、卷尺、记录表
教学过程 修注栏
问题引入: 要知道一棵大树有多高,你有办法测量吗?能不能用我们学过的数学知识和方法解决这一问题呢?今天这节课我们将一起来研究大树有多高的问题。
二、实践探素,发现规律。
(一)量量比比(小组合作完成)
提出要求:
1、在太阳光下,把几根同样长的竹竿直立在地面上,同时量出每根竹竿的影长。比较每次的测量结果,你发现了什么?
2、再把几根长度不同的竹竿直立在地面上,同时量出每根竹竿的影长。 (1)、按要求填表。
(2)、计算竹竿与影长的比值
(3)、讨论:根据每次求得的比值,你有什么发现?
(4)、得出结论:在同一地点同时测量不同的竹竿高度与影长的比值是相等的。
(二)议议做做 提出要求:
1、根据上面测量和计算的结果,假设一根3米长的竹竿,当时直立在地面的影长是多少?
(1)学生同桌交流。
(2)集体交流是让学生说说自己的想法。
2、根据上面的发现,你能想办法测出一棵大树的高度吗? 让学生在小组里交流。并指名学生说说自己的想法。
3、实践操作:现在我们一起来做一做,看看你的方法行不行。 (1)在太阳光下,先用一根竹竿的高度和影长及量出当时大树的影长,并把结果填在下表里。
(2)由学生各自算一算大树的高度。
(3)小组讨论各自的想法。
(4)提问:在测量竹竿的影长之后,如果过了一段较长的时间,再测量大树的影长。这样计算的结果还准确吗?为什么?
三、拓展延伸:
根据求大树高度经验,让学生计算某楼房、旗杆的高度。
四、小结反思
这节课你有什么收获?
提出问题后,先引导学生结合已有的知识和经验解决问题的方法,并通过比较和交流。
学生认识到用估计的方法不能得到比较准确的结果。
联系生活经验,想到虽然不能直接测量大叔的高度,但是影子的长度是可以测量的,如果能知道大树的高度和影长的关系,问题就不难解决了。
发现规律后,小组讨论,明确:在同一时间,同一地点,物体的高度和影长的比值不变,因此,此时,物体的高度和影长 成正比例的关系。
作业设计 书上实践操作
板书设计 大树有多高
在同一时间、同一地点,物体的高度和影长成正比例
教学目标 让学生通过动手实践和解决实际问题,进一步体会比的应用价值,增强数学的趣味性和挑战性。
教学重点 正比例的应用
教学难点 理解同一时间,同一地点测量
教学准备 长度不一及长度相等的竹竿、卷尺、记录表
教学过程 修注栏
问题引入: 要知道一棵大树有多高,你有办法测量吗?能不能用我们学过的数学知识和方法解决这一问题呢?今天这节课我们将一起来研究大树有多高的问题。
二、实践探素,发现规律。
(一)量量比比(小组合作完成)
提出要求:
1、在太阳光下,把几根同样长的竹竿直立在地面上,同时量出每根竹竿的影长。比较每次的测量结果,你发现了什么?
2、再把几根长度不同的竹竿直立在地面上,同时量出每根竹竿的影长。 (1)、按要求填表。
(2)、计算竹竿与影长的比值
(3)、讨论:根据每次求得的比值,你有什么发现?
(4)、得出结论:在同一地点同时测量不同的竹竿高度与影长的比值是相等的。
(二)议议做做 提出要求:
1、根据上面测量和计算的结果,假设一根3米长的竹竿,当时直立在地面的影长是多少?
(1)学生同桌交流。
(2)集体交流是让学生说说自己的想法。
2、根据上面的发现,你能想办法测出一棵大树的高度吗? 让学生在小组里交流。并指名学生说说自己的想法。
3、实践操作:现在我们一起来做一做,看看你的方法行不行。 (1)在太阳光下,先用一根竹竿的高度和影长及量出当时大树的影长,并把结果填在下表里。
(2)由学生各自算一算大树的高度。
(3)小组讨论各自的想法。
(4)提问:在测量竹竿的影长之后,如果过了一段较长的时间,再测量大树的影长。这样计算的结果还准确吗?为什么?
三、拓展延伸:
根据求大树高度经验,让学生计算某楼房、旗杆的高度。
四、小结反思
这节课你有什么收获?
提出问题后,先引导学生结合已有的知识和经验解决问题的方法,并通过比较和交流。
学生认识到用估计的方法不能得到比较准确的结果。
联系生活经验,想到虽然不能直接测量大叔的高度,但是影子的长度是可以测量的,如果能知道大树的高度和影长的关系,问题就不难解决了。
发现规律后,小组讨论,明确:在同一时间,同一地点,物体的高度和影长的比值不变,因此,此时,物体的高度和影长 成正比例的关系。
作业设计 书上实践操作
板书设计 大树有多高
在同一时间、同一地点,物体的高度和影长成正比例
