安徽省淮北市树人高级中学2020-2021学年高二下学期期末考试数学试卷 Word版含答案
文档属性
| 名称 | 安徽省淮北市树人高级中学2020-2021学年高二下学期期末考试数学试卷 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览




文档简介
树人高级中学2020-2021学年高二下学期期末考试
数学试题
考试时间:120分钟 满分:150分
一、单选题(本大题共12小题,每小题5分,满分60分)
1.对于集合A,B,我们把集合且叫做集合A与B的差集,记作.若,,则为( )
A. B. C. D.
2.已知i是虚数单位,若复数,其中,则等于( )
A.1 B.5 C. D.13
3.“”是“”成立的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件
4.函数的图象可能是( )
A. B. C. D.
5.若函数在区间上的最大值?最小值分别为?,则的值为( )
A.2 B.0 C. D.3
6.已知为二次函数,且,设数列的前项和为,则( )
A.19 B.18 C.17 D.16
7.设m,n是两条不同的直线,,是两个不同的平面,下列命题中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8.已知实数a,b,c满足,且,则( )
A. B. C. D.
9.已知,函数在上恰有5个零点,则的取值范围是( )
A. B. C. D.
10.已知函数,若不等式对恒成立,则实数的取值范围是( )
A. B. C. D.
11.已知,且,下列结论正确的是( )
①;②;③;④.
A.①④ B.②③ C.①② D.②④
12.已知函数,若存在m,n∈[2,4],且m-n≥1,使得f(m)=f(n),则实数a的取值范围是( )
A. B.
C. D.
二、填空题(本大题共4小题,每题5分,满分20分)
13.设实数,满足条件,则的最大值为 ________
14.设函数,则不等式的解集为_________.
15.设直线,分别是函数,图象上点,处的切线,与垂直相交于点,且,分别与轴相交于点,,的面积的取值范围是________.
16.已知命题p:,,若为假命题,则实数a的最大值为________.
三、解答题(共6小题,满分70分。17—21为必考题,每题12分;22题和23题任选一题作答,10分)
17.在△ABC中,角A,B,C的对边分别为a,b,c,已知.
(1)求B的大小;
(2)如图,在AC边的右侧取点D,使得,若,求当为何值时,四边形ABCD的面积最大,并求其最大值.
18.(如图1)在直角梯形中,,,,,,点在上,且.将沿折起,使得平面平面(如图2).
(1)求证:;
(2)在线段上是否存在点,使得平面?若存在,求的值;若不存在,请说明理由.
19.椭圆的离心率是,过点作斜率为k的直线l,椭圆E与直线l交于A,B两点,当直线l垂直于y轴时.
(1)求椭圆E的方程;
若点M的坐标为,是以为底边的等腰三角形,求k的值.
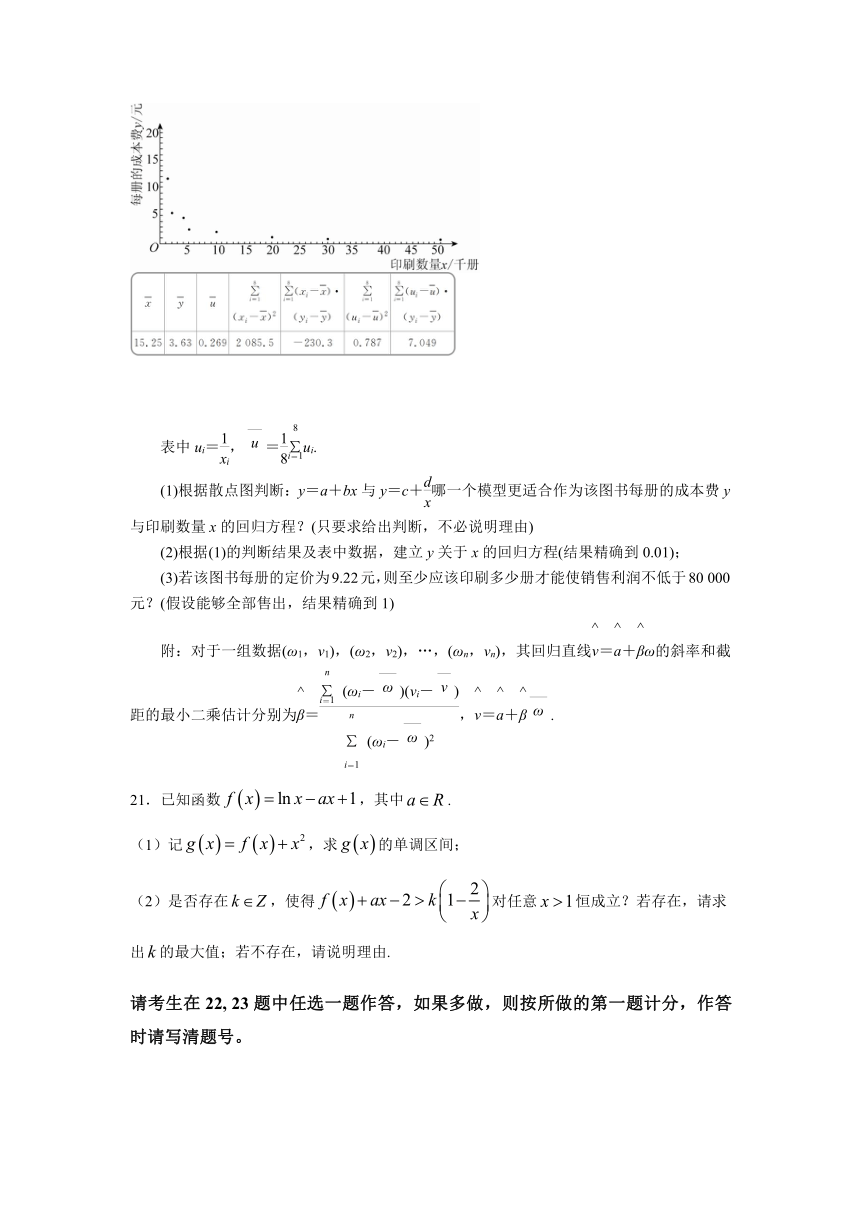
20.某公司为研究某种图书每册的成本费y(单位:元)与印刷数量x(单位:千册)的关系,收集了一些数据并进行了初步处理,得到了如图的散点图及一些统计量的值.
表中ui=,=ui.
(1)根据散点图判断:y=a+bx与y=c+哪一个模型更适合作为该图书每册的成本费y与印刷数量x的回归方程?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程(结果精确到0.01);
(3)若该图书每册的定价为9.22元,则至少应该印刷多少册才能使销售利润不低于80 000元?(假设能够全部售出,结果精确到1)
附:对于一组数据(ω1,ν1),(ω2,ν2),…,(ωn,νn),其回归直线=+ω的斜率和截距的最小二乘估计分别为=,=+.
21.已知函数,其中.
(1)记,求的单调区间;
(2)是否存在,使得对任意恒成立?若存在,请求出的最大值;若不存在,请说明理由.
请考生在22, 23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号。
22.在平面直角坐标系xOy中,曲线C1的参数方程为θ为参数),曲线C1在的变换作用下得到曲线C2.以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系(ρ>0,θ∈[0,2π)).设直线y=kx(k>0)分别与曲线C1,C2交于异于原点的P,Q两点.
(1)求曲线C1、C2的极坐标方程;
(2)设点A的坐标为(1,0),求△APQ面积的最大值.
23.已知函数
(1)求不等式的解集;
(2)当取最小值时,求使得成立的正实数的取值范围.
2020-2021学年度第二学期期末考试数学参考答案
1.B 2.B 3.B,
,
因为推不出,能推出,
所以“”是“”成立的必要不充分条件.
4.D
令,则,故为奇函数,排除A、B;
在上,有,,即,故只有D符合要求.
5.C
化简函数,得到,构造新函数,得出函数为奇函数,求得最大值与最小值之和为0,进而根据和的值域相同,即可求解.
6.C
解:由题意,设,,
即,解得,,所以,
所以,可得,当时,,
所以,又,所以,
7.C
解:对于A,若,则m,n可能平行,异面或相交,所以A错误;
对于B,若,则,可能平行,相交,所以B错误;
对于C,若,则由面面垂直的判定定理可得,所以C正确;
对于D,若,则m,n可能平行或异面。所以D错误
故选:C
8.A
设,则,
当时,,单调递增,当时,,单调递减,
,即,
所以,所以,即,
又,所以,由,所以,
所以,即,所以,所以.
9.A
解:,,
令,则
由题意得在上恰有5个根,
即,在上恰有5个根,
由的性质可得:,解得:.
10.D
,
,可得是奇函数,
又,所以在上单调递增,
由得,
即对恒成立.
当时显然成立;当时,需,得,
综上可得,
11.A
解:由条件可得,又函数在上单调递增,所以,
故,
又在上单调递增,所以,即,所以①④正确.
12.B
由题意,,
令可得,则,解得,
所以当时,,函数单调递增;
当时,,函数单调递减;
又,且,所以,
因为,,,
①若,则只需使,
即,解得;
②若,则需使,
即,解得;
综上,.
13.4
14.
当时,是增函数,此时;
当时, 是增函数,此时,所以函数是单调递增函数,
,解得:,
所以不等式的解集是.故答案为:
15.
由题意可知,,且明显地,分别在分段函数的两段上
设,且
, ,即:
方程为:;方程为:
,
联立可得点横坐标为:
且在上单调递减
,即的面积的取值范围为:
本题正确结果:
.
17.(1);(2)当时,四边形ABCD的面积取得最大值.
(1)在△ABC中,由正弦定理得,
所以,
所以.因为,所以.
又,故.
(2)由(1)知,且,所以△ABC为等边三角形.
设,则在△ACD中,由余弦定理得,
所以,
四边形ABCD的面积.
因为,所以.当,即时,.
所以当时,四边形ABCD的面积取得最大值.
18(1)证明见解析;(2)存在,.
(1)在梯形中,取的中点,连接,,如图所示
所以,,
又因为,所以,即.
在图2中,
因为平面平面,,
所以平面.
又因为平面,所以.
(2)在上取一点的,满足,
在上取一点的,满足,连接,如图所示:
因为,,所以四边形为平行四边形,
所以.
又因为平面,平面,所以平面,
因为,所以.
又因为平面,平面,所以平面,
又因为平面,平面,,
所以平面平面.
又因为平面,所以平面.
所以.
19.(1) ;(2)
解:(1)因为椭圆的离心率为,则,
此时椭圆,代得
当直线过点垂直y轴时,
则,得,
所以椭圆方程为:.
(2)设,,的中点,
由消去得:,显然,
所以,,
是以为底边的等腰三角形,则
当时,显然不成立,与题意不符.
当时,直线的斜率显然存在,所以,即
化简得,解得,
综上所述,所求的值为.
20.解 (1)由散点图判断,y=c+更适合.
(2)令u=,先建立y关于u的线性回归方程,由于=≈8.957≈8.96,
所以=-·=3.63-8.957×0.269≈1.22,所以y关于u的线性回归方程为=1.22+8.96u,所以y关于x的回归方程为=1.22+.
(3)假设印刷x千册,依题意得,
9.22x-x≥80,
解得x≥11.12,所以至少印刷11 120册才能使销售利润不低于80 000元.
21.(1)答案见解析;(2)不存在,理由见解析.
(1)(),
则
设,∵
①即时,在单调递增;
②即或,
时,,,∵在恒成立,在单调递增;
时,,,,,在和单调递增,单调递减,
综上① 时,在单调递增;
② 时,在和单调递增,在单调递减.
(2)由已知得,即为,
即(),
令(),则,
当时,,所以在上单调递增,,即,矛盾,故舍去;
当时,由,得,由,得,所以在上单调递减,单调递增,
所以(),
即当()恒成立,求的最大值.
令,则,
当,即时,单调递增,
当,即时,单调递减,
所以,
因为,又,,
所以不存在整数使成立,
综上所述,不存在满足条件的整数.
22.(1)ρ=2cosθ,ρ=4cosθ;(2).
解:(1)曲线C1的参数方程为(θ为参数),
转换为直角坐标方程为,
根据,转换为极坐标方程为ρ=2cosθ,
曲线C1在的变换作用下得到曲线C2,
即,
根据,转化为极坐标方程为ρ=4cosθ.
(2)直线y=kx(k>0)转换为极坐标方程为θ=α(0),
所以.
当时,的最大值为.
23.(1);(2).
(1)由不等式,可得,
可化为或或,
解,得或或,
综上知不等式的解集为.
(2)因为,
当且仅当,即时,等号成立.
故当时,,
法一:当取最小值时,,即,
所以,即,解得,
故所求m的取值范围.
法二:
因为,所以,所以,
所以,即,所以,
故所求m的取值范围
数学试题
考试时间:120分钟 满分:150分
一、单选题(本大题共12小题,每小题5分,满分60分)
1.对于集合A,B,我们把集合且叫做集合A与B的差集,记作.若,,则为( )
A. B. C. D.
2.已知i是虚数单位,若复数,其中,则等于( )
A.1 B.5 C. D.13
3.“”是“”成立的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件
4.函数的图象可能是( )
A. B. C. D.
5.若函数在区间上的最大值?最小值分别为?,则的值为( )
A.2 B.0 C. D.3
6.已知为二次函数,且,设数列的前项和为,则( )
A.19 B.18 C.17 D.16
7.设m,n是两条不同的直线,,是两个不同的平面,下列命题中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8.已知实数a,b,c满足,且,则( )
A. B. C. D.
9.已知,函数在上恰有5个零点,则的取值范围是( )
A. B. C. D.
10.已知函数,若不等式对恒成立,则实数的取值范围是( )
A. B. C. D.
11.已知,且,下列结论正确的是( )
①;②;③;④.
A.①④ B.②③ C.①② D.②④
12.已知函数,若存在m,n∈[2,4],且m-n≥1,使得f(m)=f(n),则实数a的取值范围是( )
A. B.
C. D.
二、填空题(本大题共4小题,每题5分,满分20分)
13.设实数,满足条件,则的最大值为 ________
14.设函数,则不等式的解集为_________.
15.设直线,分别是函数,图象上点,处的切线,与垂直相交于点,且,分别与轴相交于点,,的面积的取值范围是________.
16.已知命题p:,,若为假命题,则实数a的最大值为________.
三、解答题(共6小题,满分70分。17—21为必考题,每题12分;22题和23题任选一题作答,10分)
17.在△ABC中,角A,B,C的对边分别为a,b,c,已知.
(1)求B的大小;
(2)如图,在AC边的右侧取点D,使得,若,求当为何值时,四边形ABCD的面积最大,并求其最大值.
18.(如图1)在直角梯形中,,,,,,点在上,且.将沿折起,使得平面平面(如图2).
(1)求证:;
(2)在线段上是否存在点,使得平面?若存在,求的值;若不存在,请说明理由.
19.椭圆的离心率是,过点作斜率为k的直线l,椭圆E与直线l交于A,B两点,当直线l垂直于y轴时.
(1)求椭圆E的方程;
若点M的坐标为,是以为底边的等腰三角形,求k的值.
20.某公司为研究某种图书每册的成本费y(单位:元)与印刷数量x(单位:千册)的关系,收集了一些数据并进行了初步处理,得到了如图的散点图及一些统计量的值.
表中ui=,=ui.
(1)根据散点图判断:y=a+bx与y=c+哪一个模型更适合作为该图书每册的成本费y与印刷数量x的回归方程?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程(结果精确到0.01);
(3)若该图书每册的定价为9.22元,则至少应该印刷多少册才能使销售利润不低于80 000元?(假设能够全部售出,结果精确到1)
附:对于一组数据(ω1,ν1),(ω2,ν2),…,(ωn,νn),其回归直线=+ω的斜率和截距的最小二乘估计分别为=,=+.
21.已知函数,其中.
(1)记,求的单调区间;
(2)是否存在,使得对任意恒成立?若存在,请求出的最大值;若不存在,请说明理由.
请考生在22, 23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号。
22.在平面直角坐标系xOy中,曲线C1的参数方程为θ为参数),曲线C1在的变换作用下得到曲线C2.以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系(ρ>0,θ∈[0,2π)).设直线y=kx(k>0)分别与曲线C1,C2交于异于原点的P,Q两点.
(1)求曲线C1、C2的极坐标方程;
(2)设点A的坐标为(1,0),求△APQ面积的最大值.
23.已知函数
(1)求不等式的解集;
(2)当取最小值时,求使得成立的正实数的取值范围.
2020-2021学年度第二学期期末考试数学参考答案
1.B 2.B 3.B,
,
因为推不出,能推出,
所以“”是“”成立的必要不充分条件.
4.D
令,则,故为奇函数,排除A、B;
在上,有,,即,故只有D符合要求.
5.C
化简函数,得到,构造新函数,得出函数为奇函数,求得最大值与最小值之和为0,进而根据和的值域相同,即可求解.
6.C
解:由题意,设,,
即,解得,,所以,
所以,可得,当时,,
所以,又,所以,
7.C
解:对于A,若,则m,n可能平行,异面或相交,所以A错误;
对于B,若,则,可能平行,相交,所以B错误;
对于C,若,则由面面垂直的判定定理可得,所以C正确;
对于D,若,则m,n可能平行或异面。所以D错误
故选:C
8.A
设,则,
当时,,单调递增,当时,,单调递减,
,即,
所以,所以,即,
又,所以,由,所以,
所以,即,所以,所以.
9.A
解:,,
令,则
由题意得在上恰有5个根,
即,在上恰有5个根,
由的性质可得:,解得:.
10.D
,
,可得是奇函数,
又,所以在上单调递增,
由得,
即对恒成立.
当时显然成立;当时,需,得,
综上可得,
11.A
解:由条件可得,又函数在上单调递增,所以,
故,
又在上单调递增,所以,即,所以①④正确.
12.B
由题意,,
令可得,则,解得,
所以当时,,函数单调递增;
当时,,函数单调递减;
又,且,所以,
因为,,,
①若,则只需使,
即,解得;
②若,则需使,
即,解得;
综上,.
13.4
14.
当时,是增函数,此时;
当时, 是增函数,此时,所以函数是单调递增函数,
,解得:,
所以不等式的解集是.故答案为:
15.
由题意可知,,且明显地,分别在分段函数的两段上
设,且
, ,即:
方程为:;方程为:
,
联立可得点横坐标为:
且在上单调递减
,即的面积的取值范围为:
本题正确结果:
.
17.(1);(2)当时,四边形ABCD的面积取得最大值.
(1)在△ABC中,由正弦定理得,
所以,
所以.因为,所以.
又,故.
(2)由(1)知,且,所以△ABC为等边三角形.
设,则在△ACD中,由余弦定理得,
所以,
四边形ABCD的面积.
因为,所以.当,即时,.
所以当时,四边形ABCD的面积取得最大值.
18(1)证明见解析;(2)存在,.
(1)在梯形中,取的中点,连接,,如图所示
所以,,
又因为,所以,即.
在图2中,
因为平面平面,,
所以平面.
又因为平面,所以.
(2)在上取一点的,满足,
在上取一点的,满足,连接,如图所示:
因为,,所以四边形为平行四边形,
所以.
又因为平面,平面,所以平面,
因为,所以.
又因为平面,平面,所以平面,
又因为平面,平面,,
所以平面平面.
又因为平面,所以平面.
所以.
19.(1) ;(2)
解:(1)因为椭圆的离心率为,则,
此时椭圆,代得
当直线过点垂直y轴时,
则,得,
所以椭圆方程为:.
(2)设,,的中点,
由消去得:,显然,
所以,,
是以为底边的等腰三角形,则
当时,显然不成立,与题意不符.
当时,直线的斜率显然存在,所以,即
化简得,解得,
综上所述,所求的值为.
20.解 (1)由散点图判断,y=c+更适合.
(2)令u=,先建立y关于u的线性回归方程,由于=≈8.957≈8.96,
所以=-·=3.63-8.957×0.269≈1.22,所以y关于u的线性回归方程为=1.22+8.96u,所以y关于x的回归方程为=1.22+.
(3)假设印刷x千册,依题意得,
9.22x-x≥80,
解得x≥11.12,所以至少印刷11 120册才能使销售利润不低于80 000元.
21.(1)答案见解析;(2)不存在,理由见解析.
(1)(),
则
设,∵
①即时,在单调递增;
②即或,
时,,,∵在恒成立,在单调递增;
时,,,,,在和单调递增,单调递减,
综上① 时,在单调递增;
② 时,在和单调递增,在单调递减.
(2)由已知得,即为,
即(),
令(),则,
当时,,所以在上单调递增,,即,矛盾,故舍去;
当时,由,得,由,得,所以在上单调递减,单调递增,
所以(),
即当()恒成立,求的最大值.
令,则,
当,即时,单调递增,
当,即时,单调递减,
所以,
因为,又,,
所以不存在整数使成立,
综上所述,不存在满足条件的整数.
22.(1)ρ=2cosθ,ρ=4cosθ;(2).
解:(1)曲线C1的参数方程为(θ为参数),
转换为直角坐标方程为,
根据,转换为极坐标方程为ρ=2cosθ,
曲线C1在的变换作用下得到曲线C2,
即,
根据,转化为极坐标方程为ρ=4cosθ.
(2)直线y=kx(k>0)转换为极坐标方程为θ=α(0),
所以.
当时,的最大值为.
23.(1);(2).
(1)由不等式,可得,
可化为或或,
解,得或或,
综上知不等式的解集为.
(2)因为,
当且仅当,即时,等号成立.
故当时,,
法一:当取最小值时,,即,
所以,即,解得,
故所求m的取值范围.
法二:
因为,所以,所以,
所以,即,所以,
故所求m的取值范围
同课章节目录
