科学命题同步练习之21.2.1.2配方法(含解析)
文档属性
| 名称 | 科学命题同步练习之21.2.1.2配方法(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
科学命题同步练习之21.2.1配方法
一、选择题
用配方法解下列方程,其中应在方程的左右两边同时加上
的是
A.
B.
C.
D.
用配方法解方程
时,原方程应变形为
A.
B.
C.
D.
用配方法解下列方程时,配方有错误的是
A.
化为
B.
化为
C.
化为
D.
化为
已知方程
可以配方成
的形式,那么
可以配成的是
A.
B.
C.
D.
已知实数
,
满足
,则
的值为
A.
B.
C.
或
D.
或
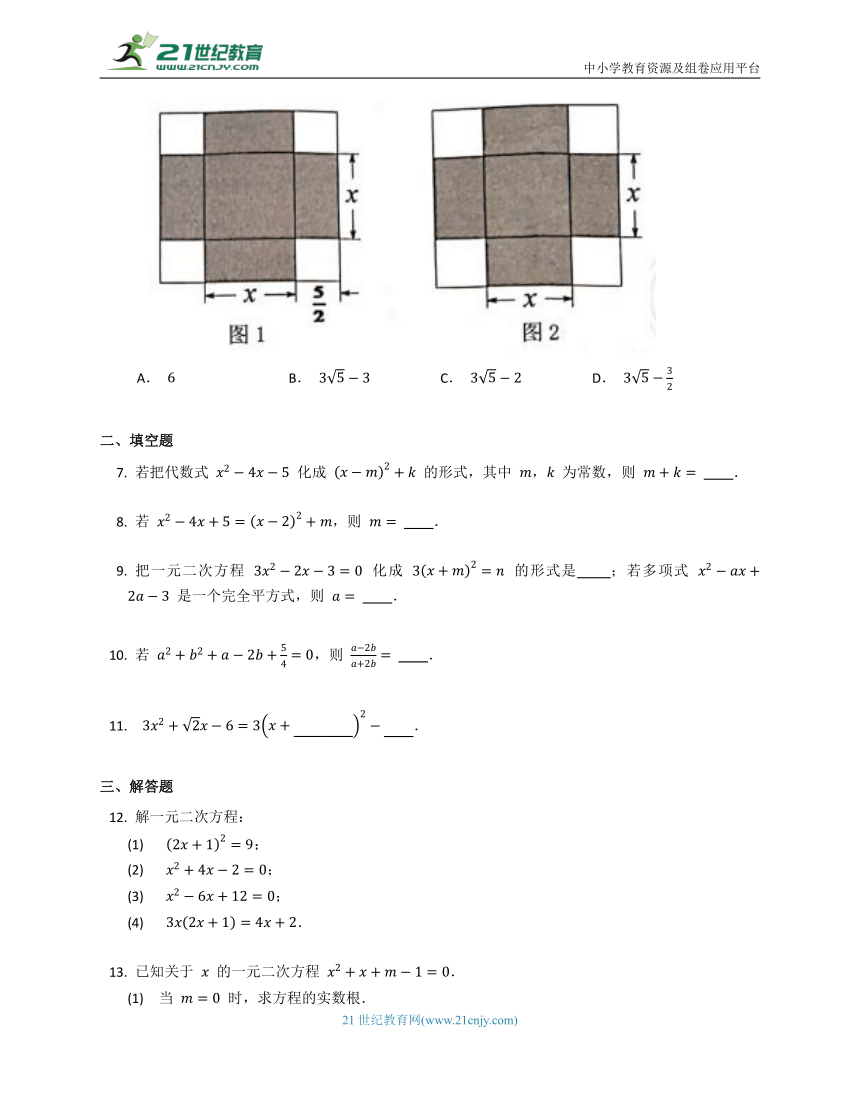
《代数学》中记载,形如
的方程,求正数解的几何方法是:“如图
,先构造一个面积为
的正方形,再以正方形的边长为一边向外构造四个面积为
的矩形,得到大正方形的面积为
,则该方程的正数解为
”,小聪按此方法解关于
的方程
时,构造出如图
所示的图形,己知阴影部分的面积为
,则该方程的正数解为
A.
B.
C.
D.
二、填空题
若把代数式
化成
的形式,其中
,
为常数,则
.
若
,则
.
把一元二次方程
化成
的形式是
;若多项式
是一个完全平方式,则
.
若
,则
.
.
三、解答题
解一元二次方程:
(1)
;
(2)
;
(3)
;
(4)
.
已知关于
的一元二次方程
.
(1)
当
时,求方程的实数根.
(2)
若方程有两个不相等的实数根,求实数
的取值范围.
实际问题:
某商场为鼓励消费,设计了投资活动.方案如下:根据不同的消费金额,每次抽奖时可以从
张面值分别为
元、
元、
元、
、
元的奖券中(面值为整数),一次任意抽取
张、
张、
张、
等若干张奖券,奖券的面值金额之和即为优惠金额.某顾客获得了一次抽取
张奖券的机会,小明想知道该顾客共有多少种不同的优惠金额?
问题建模:
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有多少种不同的结果?
模型探究:
我们采取一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
(1)
探究一:
()从
,,
这
个整数中任取
个整数,这
个整数之和共有多少种不同的结果?
表①
如表①,所取的
个整数之和可以为
,,,也就是从
到
的连续整数,其中最小是
,最大是
,所以共有
种不同的结果.
()从
,,,
这
个整数中任取
个整数,这
个整数之和共有多少种不同的结果?
表②
如表②,所取的
个整数之和可以为
,,,,,也就是从
到
的连续整数,其中最小是
,最大是
,所以共有
种不同的结果.
()从
,,,,
这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
()从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(2)
探究二:
()从
,,,
这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
()从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(3)
探究三:
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(4)
归纳结论:
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(5)
问题解决:
从
张面值分别为
元、
元、
元、
、
元的奖券中(面值为整数),一次任意抽取
张奖券,共有
种不同的优惠金额.
(6)
拓展延伸:
()从
,,,,
这
个整数中任取多少个整数,使得取出的这些整数之和共有
种不同的结果?(写出解答过程)
()从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
答案
一、选择题
1.
【答案】B
【解析】A选项中,
本方程的一次项系数是
,
等式两边同时加上一次项系数一半的平方
,故本选项错误;
B选项中,
本方程的一次项系数是
,
等式两边同时加上一次项系数一半的平方
,故本选项正确;
C选项中,
本方程的一次项系数是
,
等式两边同时加上一次项系数一半的平方
,故本选项错误;
D选项中,
将该方程的二次项系数化为
得:,
本方程的一次项系数是
,
等式两边同时加上一次项系数一半的平方
,故本选项错误.
【知识点】配方法
2.
【答案】B
【解析】方程移项得:,
配方得:,
即
.
【知识点】配方法
3.
【答案】A
【知识点】配方法
4.
【答案】D
【解析】
可化为
,由题意可知
,
可化为
,即
,
可以配成
.
【知识点】配方法
5.
【答案】A
【解析】
,
,
,
即:,
,
又
,
.
【知识点】配方法
6.
【答案】B
【解析】由题意得:,
解方程得:,
,
或
,
或
,
该方程的正数解为:,
故答案为:B.
【知识点】配方法
二、填空题
7.
【答案】
【解析】
,
,,
.
【知识点】配方法
8.
【答案】
【知识点】配方法
9.
【答案】
;
或
【解析】根据题意,一元二次方程
化成
,
括号里面配方得,,即
;
多项式
是一个完全平方式,
,
解得
.
【知识点】配方法
10.
【答案】
【知识点】配方法
11.
【答案】
;
【知识点】配方法
三、解答题
12.
【答案】
(1)
所以
(2)
所以
(3)
,
所以方程没有实数解.
(4)
所以
【知识点】公式法、直接开平方法、配方法、因式分解法
13.
【答案】
(1)
当
时,原方程为
,
则
,
,
,
解得:,.
(2)
若方程有两个不相等的实数根,则
,
即
,解得:.
【知识点】配方法、一元二次方程根的判别式
14.
【答案】
(1)
;
(2)
;
(3)
(4)
(5)
(6)
()
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
当
,有
,
,
,
或
,
或
.
从
,,,,
这
个整数中任取
个或
个整数,使得取出的这些整数之和共有
种不同的结果.
()
【解析】
(1)
()如下表:所取的
个整数之和可以为
,,,,,,
也就是从
到
的连续整数,其中最小是
,最大是
,所以共有
种不同的结果.
()从
,,,,(
为整数,且
)这个整数中任取
个整数,这
个整数之和的最小值是
,和的最大值是
,所以一共有
种.
(2)
()从
,,,
这
个整数中任取
个整数,如下表:从
,,,
这
个整数中任取
个整数,这
个整数之和共有
种,
()从
,,,,
这
个整数中任取
个整数,
这
个整数之和的最小值是
,和的最大值是
,
从
,,,,
这
个整数中任取
个整数,这
个整数之和共有
种,
从而从
,,,,(
为整数,且
)这
个整数中任取
个整数,
这
个整数之和的最小值是
,和的最大值是
,
所以一共有
种.
(3)
从
,,,,
这
个整数中任取
个整数,这
个整数之和最小是
,最大是
,
这
个整数之和一共有
种,
从
,,,,,
这
个整数中任取
个整数,这
个整数之和最小是
,最大是
,
这
个整数之和一共有
种,
从
,,,,(
为整数,且
)这
个整数中任取
个整数,
这
个整数之和的最小值是
,和的最大值是
,
一共有
种不同的结果.
(4)
由探究一,从
,,,,(
为整数,且
)这个
整数中任取
个整数,这
个整数之和共有
种.
探究二,从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种,
探究三,从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
从而可得:
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(5)
从
张面值分别为
元、
元、
元、
、
元的奖券中(面值为整数),
一次任意抽取
张奖券,这
张奖券和的最小值是
,和的最大值是
,
共有
种不同的优惠金额.
(6)
()由探究可知:从
,,,,(
为整数,且
)这
个整数中任取
个整数,等同于从
,,,,(
为整数,且
)这
个整数中任取
个整数,
所以:从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
【知识点】逻辑推理、用代数式表示规律、简单的代数式求值、配方法
21世纪教育网(www.21cnjy.com)
科学命题同步练习之21.2.1配方法
一、选择题
用配方法解下列方程,其中应在方程的左右两边同时加上
的是
A.
B.
C.
D.
用配方法解方程
时,原方程应变形为
A.
B.
C.
D.
用配方法解下列方程时,配方有错误的是
A.
化为
B.
化为
C.
化为
D.
化为
已知方程
可以配方成
的形式,那么
可以配成的是
A.
B.
C.
D.
已知实数
,
满足
,则
的值为
A.
B.
C.
或
D.
或
《代数学》中记载,形如
的方程,求正数解的几何方法是:“如图
,先构造一个面积为
的正方形,再以正方形的边长为一边向外构造四个面积为
的矩形,得到大正方形的面积为
,则该方程的正数解为
”,小聪按此方法解关于
的方程
时,构造出如图
所示的图形,己知阴影部分的面积为
,则该方程的正数解为
A.
B.
C.
D.
二、填空题
若把代数式
化成
的形式,其中
,
为常数,则
.
若
,则
.
把一元二次方程
化成
的形式是
;若多项式
是一个完全平方式,则
.
若
,则
.
.
三、解答题
解一元二次方程:
(1)
;
(2)
;
(3)
;
(4)
.
已知关于
的一元二次方程
.
(1)
当
时,求方程的实数根.
(2)
若方程有两个不相等的实数根,求实数
的取值范围.
实际问题:
某商场为鼓励消费,设计了投资活动.方案如下:根据不同的消费金额,每次抽奖时可以从
张面值分别为
元、
元、
元、
、
元的奖券中(面值为整数),一次任意抽取
张、
张、
张、
等若干张奖券,奖券的面值金额之和即为优惠金额.某顾客获得了一次抽取
张奖券的机会,小明想知道该顾客共有多少种不同的优惠金额?
问题建模:
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有多少种不同的结果?
模型探究:
我们采取一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
(1)
探究一:
()从
,,
这
个整数中任取
个整数,这
个整数之和共有多少种不同的结果?
表①
如表①,所取的
个整数之和可以为
,,,也就是从
到
的连续整数,其中最小是
,最大是
,所以共有
种不同的结果.
()从
,,,
这
个整数中任取
个整数,这
个整数之和共有多少种不同的结果?
表②
如表②,所取的
个整数之和可以为
,,,,,也就是从
到
的连续整数,其中最小是
,最大是
,所以共有
种不同的结果.
()从
,,,,
这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
()从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(2)
探究二:
()从
,,,
这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
()从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(3)
探究三:
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(4)
归纳结论:
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(5)
问题解决:
从
张面值分别为
元、
元、
元、
、
元的奖券中(面值为整数),一次任意抽取
张奖券,共有
种不同的优惠金额.
(6)
拓展延伸:
()从
,,,,
这
个整数中任取多少个整数,使得取出的这些整数之和共有
种不同的结果?(写出解答过程)
()从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
答案
一、选择题
1.
【答案】B
【解析】A选项中,
本方程的一次项系数是
,
等式两边同时加上一次项系数一半的平方
,故本选项错误;
B选项中,
本方程的一次项系数是
,
等式两边同时加上一次项系数一半的平方
,故本选项正确;
C选项中,
本方程的一次项系数是
,
等式两边同时加上一次项系数一半的平方
,故本选项错误;
D选项中,
将该方程的二次项系数化为
得:,
本方程的一次项系数是
,
等式两边同时加上一次项系数一半的平方
,故本选项错误.
【知识点】配方法
2.
【答案】B
【解析】方程移项得:,
配方得:,
即
.
【知识点】配方法
3.
【答案】A
【知识点】配方法
4.
【答案】D
【解析】
可化为
,由题意可知
,
可化为
,即
,
可以配成
.
【知识点】配方法
5.
【答案】A
【解析】
,
,
,
即:,
,
又
,
.
【知识点】配方法
6.
【答案】B
【解析】由题意得:,
解方程得:,
,
或
,
或
,
该方程的正数解为:,
故答案为:B.
【知识点】配方法
二、填空题
7.
【答案】
【解析】
,
,,
.
【知识点】配方法
8.
【答案】
【知识点】配方法
9.
【答案】
;
或
【解析】根据题意,一元二次方程
化成
,
括号里面配方得,,即
;
多项式
是一个完全平方式,
,
解得
.
【知识点】配方法
10.
【答案】
【知识点】配方法
11.
【答案】
;
【知识点】配方法
三、解答题
12.
【答案】
(1)
所以
(2)
所以
(3)
,
所以方程没有实数解.
(4)
所以
【知识点】公式法、直接开平方法、配方法、因式分解法
13.
【答案】
(1)
当
时,原方程为
,
则
,
,
,
解得:,.
(2)
若方程有两个不相等的实数根,则
,
即
,解得:.
【知识点】配方法、一元二次方程根的判别式
14.
【答案】
(1)
;
(2)
;
(3)
(4)
(5)
(6)
()
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
当
,有
,
,
,
或
,
或
.
从
,,,,
这
个整数中任取
个或
个整数,使得取出的这些整数之和共有
种不同的结果.
()
【解析】
(1)
()如下表:所取的
个整数之和可以为
,,,,,,
也就是从
到
的连续整数,其中最小是
,最大是
,所以共有
种不同的结果.
()从
,,,,(
为整数,且
)这个整数中任取
个整数,这
个整数之和的最小值是
,和的最大值是
,所以一共有
种.
(2)
()从
,,,
这
个整数中任取
个整数,如下表:从
,,,
这
个整数中任取
个整数,这
个整数之和共有
种,
()从
,,,,
这
个整数中任取
个整数,
这
个整数之和的最小值是
,和的最大值是
,
从
,,,,
这
个整数中任取
个整数,这
个整数之和共有
种,
从而从
,,,,(
为整数,且
)这
个整数中任取
个整数,
这
个整数之和的最小值是
,和的最大值是
,
所以一共有
种.
(3)
从
,,,,
这
个整数中任取
个整数,这
个整数之和最小是
,最大是
,
这
个整数之和一共有
种,
从
,,,,,
这
个整数中任取
个整数,这
个整数之和最小是
,最大是
,
这
个整数之和一共有
种,
从
,,,,(
为整数,且
)这
个整数中任取
个整数,
这
个整数之和的最小值是
,和的最大值是
,
一共有
种不同的结果.
(4)
由探究一,从
,,,,(
为整数,且
)这个
整数中任取
个整数,这
个整数之和共有
种.
探究二,从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种,
探究三,从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
从而可得:
从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
(5)
从
张面值分别为
元、
元、
元、
、
元的奖券中(面值为整数),
一次任意抽取
张奖券,这
张奖券和的最小值是
,和的最大值是
,
共有
种不同的优惠金额.
(6)
()由探究可知:从
,,,,(
为整数,且
)这
个整数中任取
个整数,等同于从
,,,,(
为整数,且
)这
个整数中任取
个整数,
所以:从
,,,,(
为整数,且
)这
个整数中任取
个整数,这
个整数之和共有
种不同的结果.
【知识点】逻辑推理、用代数式表示规律、简单的代数式求值、配方法
21世纪教育网(www.21cnjy.com)
同课章节目录
