2020-2021学年人教版数学九年级上册22.2.2二次函数与一元二次方程课件(16张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学九年级上册22.2.2二次函数与一元二次方程课件(16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 664.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 21:35:14 | ||
图片预览



文档简介
§22.2二次函数与一元二次方程
(1)一次函数y=x+2的图象与x轴的交点为( , )
一元一次方程x+2=0的根为_______
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为________
回忆: 一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根
求一次函数的交点问题可以转化为一元一次方程去解决
-2 0
-2
2 0
2
1、一次函数与一元一次方程的关系
2、一元二次方程ax2+bx+c=0的根的情况可由_____ 确定。
> 0
= 0
< 0
有两个不相等的实数根
有两个相等的实数根
没有实数根
b2- 4ac
y=x2-2x-3
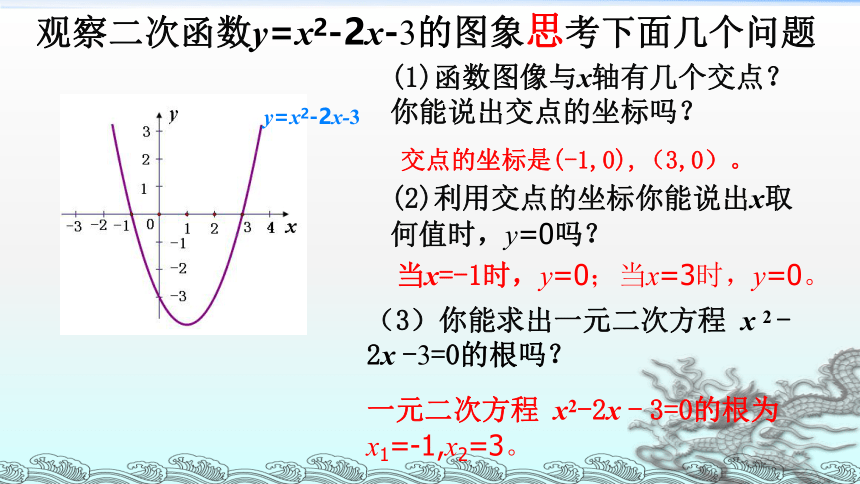
观察二次函数y=x2-2x-3的图象思考下面几个问题
一元二次方程 x2-2x - 3=0的根为x1=-1,x2=3。
交点的坐标是(-1,0),(3,0)。
(3)你能求出一元二次方程 x 2 -2x -3=0的根吗?
当x=-1时,y=0;当x=3时,y=0。
(2)利用交点的坐标你能说出x取何值时,y=0吗?
(1)函数图像与x轴有几个交点?你能说出交点的坐标吗?
y=x2-2x-3
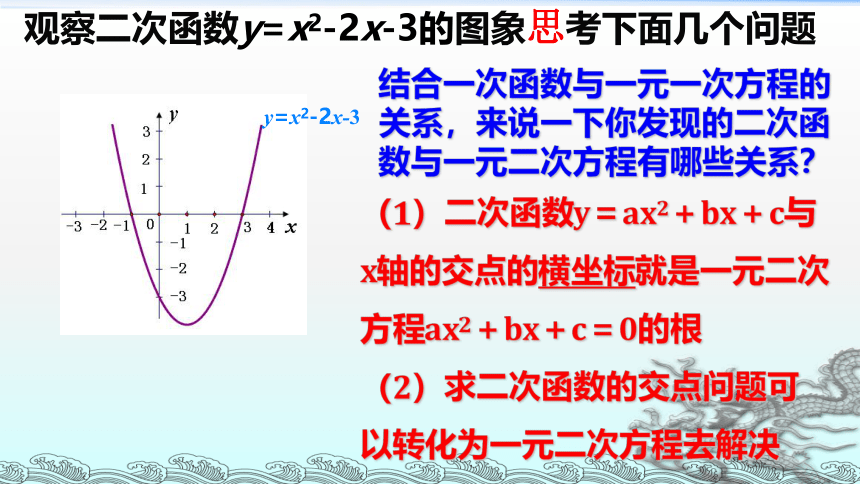
观察二次函数y=x2-2x-3的图象思考下面几个问题
(1)二次函数y=ax2+bx+c与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根
(2)求二次函数的交点问题可以转化为一元二次方程去解决
结合一次函数与一元一次方程的关系,来说一下你发现的二次函数与一元二次方程有哪些关系?
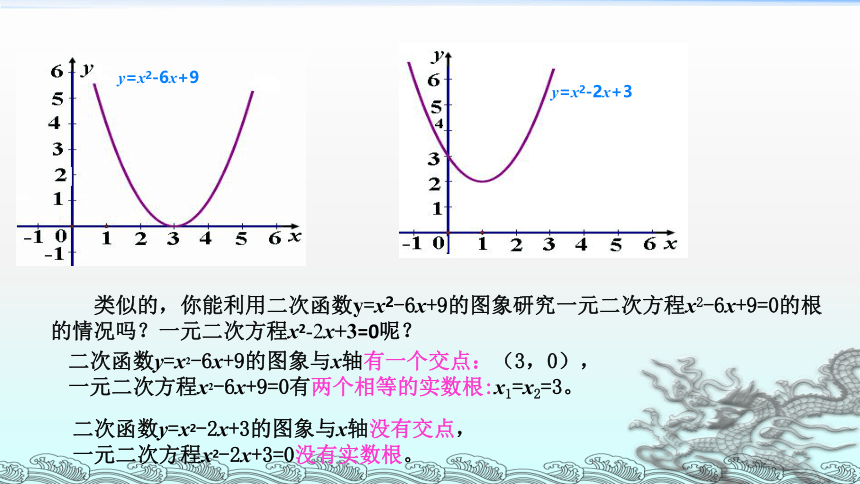
二次函数y=x2-6x+9的图象与x轴有一个交点:(3,0),
一元二次方程x2-6x+9=0有两个相等的实数根:x1=x2=3。
二次函数y=x2-2x+3的图象与x轴没有交点,
一元二次方程x2-2x+3=0没有实数根。
类似的,你能利用二次函数y=x2-6x+9的图象研究一元二次方程x2-6x+9=0的根的情况吗?一元二次方程x2-2x+3=0呢?
y=x2-6x+9
y=x2-2x+3
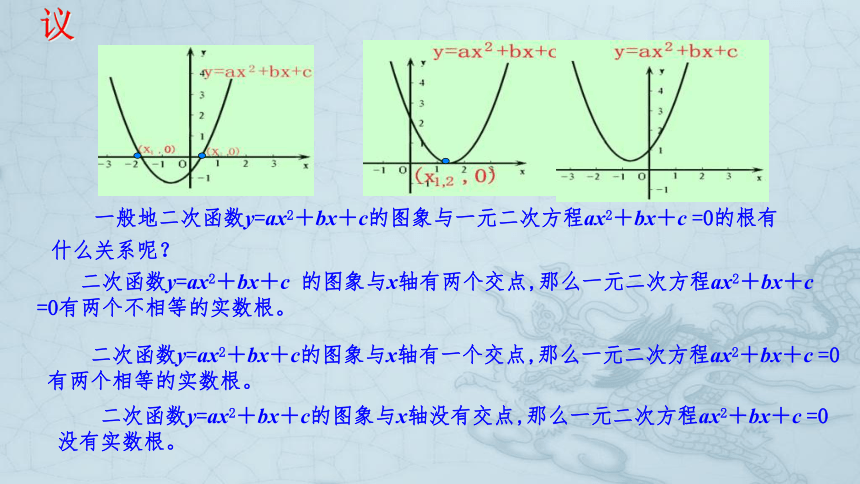
一般地二次函数y=ax2+bx+c的图象与一元二次方程ax2+bx+c =0的根有什么关系呢?
二次函数y=ax2+bx+c 的图象与x轴有两个交点,那么一元二次方程ax2+bx+c =0有两个不相等的实数根。
二次函数y=ax2+bx+c的图象与x轴有一个交点,那么一元二次方程ax2+bx+c =0有两个相等的实数根。
二次函数y=ax2+bx+c的图象与x轴没有交点,那么一元二次方程ax2+bx+c =0没有实数根。
议
一元二次方程ax2+bx+c =0有两个不相等的实数根,你又能得到什么呢?
一元二次方程ax2+bx+c=0有两个相等的实数根,那么二次函数y=ax2+bx+c的图象与x轴有一个交点。
一元二次方程ax2+bx+c没有实数根,那么二次函数y=ax2+bx+c的图象与x轴没有交点。
议
可以知道:二次函数y=ax2+bx+c的图象与x轴有两个交点。
例1. 求二次函数y=x2+4x-5与x轴的交点坐标
解:令y=0
则x2+4x-5 =0
解得,x1= -5 ,x2 = 1
∴交点坐标为:(-5,0),(1,0)
若知道一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是
A( ), B( )
X1,0
X2,0
例2. 判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y=x2-4x+4;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
1.不与x轴相交的抛物线是( )
A.y=2x2 – 3 B.y= - 2 x2 + 3
C.y= - x2 – 2x D.y=-2(x+1)2 - 3
2.不论x为何值时,函数y=ax2+bx+c(a≠0)
的值永远为正的条件是____
3.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定
D
a>0且Δ <0
C
.
;
.
4
对于任意实数m ,该二次函数的图象与x轴总有公共点
求证:
已知二次函数y=2x2-mx-m2
.
,
0
2
4
0
2
,
0
:
9
)
(
2
2
2
2
2
轴总有公共点
抛物线与
取何值
不论
得
令
证明
x
m
mx
y
m
m
m
m
x
\
?
=
?
+
=
D
=
-
-
=
-
Q
本节课都学了哪些内容?
(1)二次函数y=ax2+bx+c与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象和x轴交点
有两个交点
有两个相异的实数根
有一个交点
有两个相等的实数根
没有交点
没有实数根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
b2-4ac > 0
b2-4ac = 0
b2-4ac < 0
(2)
拓展:二次函数与x轴的交点个数可以借助判别式解决,那么二次函数与一次函数的交点个数又该怎么解决呢?
例如,二次函数y=x2-2x-3和一次函数y=x+2有交点吗?有几个?
分析:两个函数的交点是这两个函数的公共解,先列出方程组,消去y后,再利用判别式判断即可.
3.二次函数y=x2-x-3和一次函数y=x+b有一个公共点(即相切),求出b的值.
课后作业
P22 练习1、2
(1)一次函数y=x+2的图象与x轴的交点为( , )
一元一次方程x+2=0的根为_______
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为________
回忆: 一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根
求一次函数的交点问题可以转化为一元一次方程去解决
-2 0
-2
2 0
2
1、一次函数与一元一次方程的关系
2、一元二次方程ax2+bx+c=0的根的情况可由_____ 确定。
> 0
= 0
< 0
有两个不相等的实数根
有两个相等的实数根
没有实数根
b2- 4ac
y=x2-2x-3
观察二次函数y=x2-2x-3的图象思考下面几个问题
一元二次方程 x2-2x - 3=0的根为x1=-1,x2=3。
交点的坐标是(-1,0),(3,0)。
(3)你能求出一元二次方程 x 2 -2x -3=0的根吗?
当x=-1时,y=0;当x=3时,y=0。
(2)利用交点的坐标你能说出x取何值时,y=0吗?
(1)函数图像与x轴有几个交点?你能说出交点的坐标吗?
y=x2-2x-3
观察二次函数y=x2-2x-3的图象思考下面几个问题
(1)二次函数y=ax2+bx+c与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根
(2)求二次函数的交点问题可以转化为一元二次方程去解决
结合一次函数与一元一次方程的关系,来说一下你发现的二次函数与一元二次方程有哪些关系?
二次函数y=x2-6x+9的图象与x轴有一个交点:(3,0),
一元二次方程x2-6x+9=0有两个相等的实数根:x1=x2=3。
二次函数y=x2-2x+3的图象与x轴没有交点,
一元二次方程x2-2x+3=0没有实数根。
类似的,你能利用二次函数y=x2-6x+9的图象研究一元二次方程x2-6x+9=0的根的情况吗?一元二次方程x2-2x+3=0呢?
y=x2-6x+9
y=x2-2x+3
一般地二次函数y=ax2+bx+c的图象与一元二次方程ax2+bx+c =0的根有什么关系呢?
二次函数y=ax2+bx+c 的图象与x轴有两个交点,那么一元二次方程ax2+bx+c =0有两个不相等的实数根。
二次函数y=ax2+bx+c的图象与x轴有一个交点,那么一元二次方程ax2+bx+c =0有两个相等的实数根。
二次函数y=ax2+bx+c的图象与x轴没有交点,那么一元二次方程ax2+bx+c =0没有实数根。
议
一元二次方程ax2+bx+c =0有两个不相等的实数根,你又能得到什么呢?
一元二次方程ax2+bx+c=0有两个相等的实数根,那么二次函数y=ax2+bx+c的图象与x轴有一个交点。
一元二次方程ax2+bx+c没有实数根,那么二次函数y=ax2+bx+c的图象与x轴没有交点。
议
可以知道:二次函数y=ax2+bx+c的图象与x轴有两个交点。
例1. 求二次函数y=x2+4x-5与x轴的交点坐标
解:令y=0
则x2+4x-5 =0
解得,x1= -5 ,x2 = 1
∴交点坐标为:(-5,0),(1,0)
若知道一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是
A( ), B( )
X1,0
X2,0
例2. 判断下列二次函数图象与x轴的交点情况
(1)y=x2-1;
(2)y=-2x2+3x-9;
(3)y=x2-4x+4;
(4)y=-ax2+(a+b)x-b(a、b为常数,a≠0)
1.不与x轴相交的抛物线是( )
A.y=2x2 – 3 B.y= - 2 x2 + 3
C.y= - x2 – 2x D.y=-2(x+1)2 - 3
2.不论x为何值时,函数y=ax2+bx+c(a≠0)
的值永远为正的条件是____
3.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴交点情况是( )
A.无交点 B.只有一个交点
C.有两个交点 D.不能确定
D
a>0且Δ <0
C
.
;
.
4
对于任意实数m ,该二次函数的图象与x轴总有公共点
求证:
已知二次函数y=2x2-mx-m2
.
,
0
2
4
0
2
,
0
:
9
)
(
2
2
2
2
2
轴总有公共点
抛物线与
取何值
不论
得
令
证明
x
m
mx
y
m
m
m
m
x
\
?
=
?
+
=
D
=
-
-
=
-
Q
本节课都学了哪些内容?
(1)二次函数y=ax2+bx+c与x轴的交点的横坐标就是一元二次方程ax2+bx+c=0的根
一元二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象和x轴交点
有两个交点
有两个相异的实数根
有一个交点
有两个相等的实数根
没有交点
没有实数根
一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac
b2-4ac > 0
b2-4ac = 0
b2-4ac < 0
(2)
拓展:二次函数与x轴的交点个数可以借助判别式解决,那么二次函数与一次函数的交点个数又该怎么解决呢?
例如,二次函数y=x2-2x-3和一次函数y=x+2有交点吗?有几个?
分析:两个函数的交点是这两个函数的公共解,先列出方程组,消去y后,再利用判别式判断即可.
3.二次函数y=x2-x-3和一次函数y=x+b有一个公共点(即相切),求出b的值.
课后作业
P22 练习1、2
同课章节目录
