2020-2021学年人教版数学九年级上册22.2二次函数与一元二次方程(19张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学九年级上册22.2二次函数与一元二次方程(19张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 21:39:52 | ||
图片预览




文档简介
(第二课时)
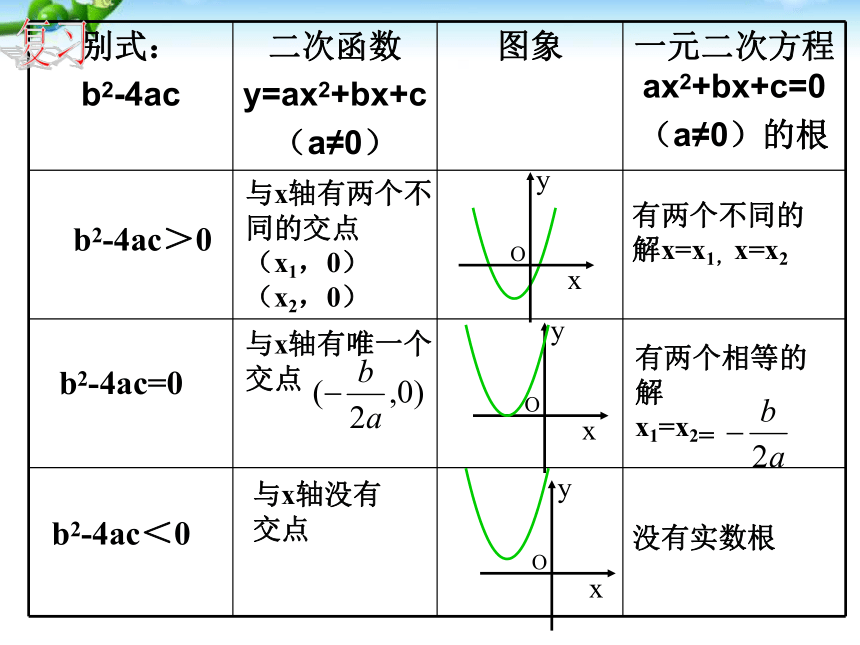
别式:
b2-4ac
二次函数
y=ax2+bx+c
(a≠0)
图象
一元二次方程ax2+bx+c=0
(a≠0)的根
x
y
O
与x轴有两个不
同的交点
(x1,0)
(x2,0)
有两个不同的解x=x1,x=x2
b2-4ac>0
x
y
O
与x轴有唯一个
交点
有两个相等的解
x1=x2=
b2-4ac=0
x
y
O
与x轴没有
交点
没有实数根
b2-4ac<0
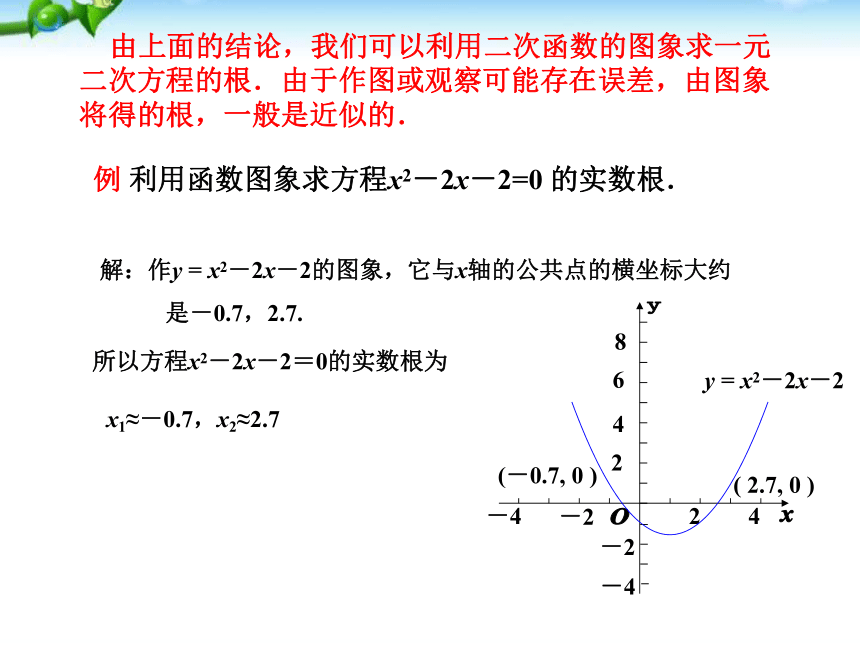
由上面的结论,我们可以利用二次函数的图象求一元二次方程的根.由于作图或观察可能存在误差,由图象将得的根,一般是近似的.
例 利用函数图象求方程x2-2x-2=0 的实数根.
解:作y = x2-2x-2的图象,它与x轴的公共点的横坐标大约
是-0.7,2.7.
所以方程x2-2x-2=0的实数根为
x1≈-0.7,x2≈2.7
-2
2
2
4
6
4
-4
8
-2
-4
y = x2-2x-2
( 2.7, 0 )
(-0.7, 0 )
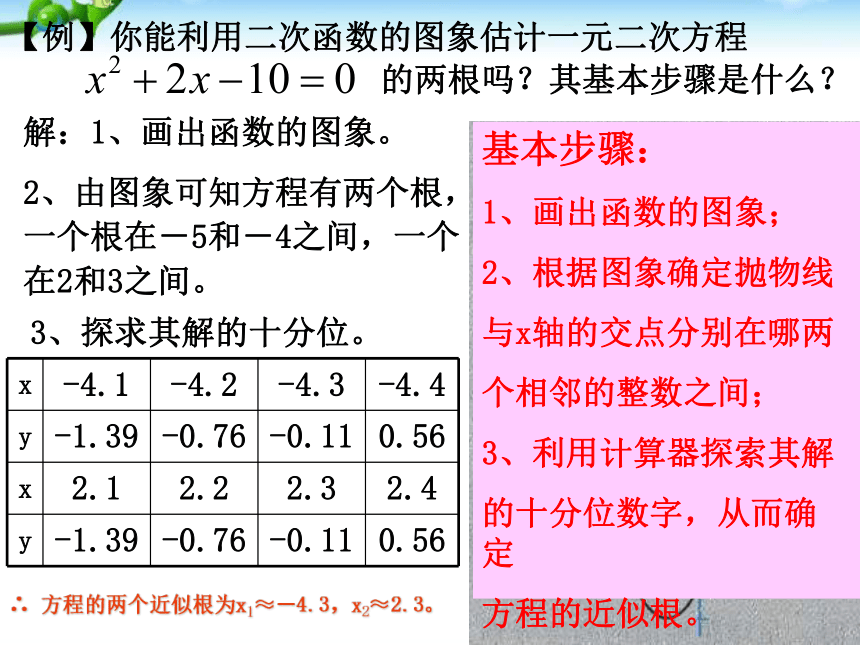
【例】你能利用二次函数的图象估计一元二次方程
的两根吗?其基本步骤是什么?
解:1、画出函数的图象。
2、由图象可知方程有两个根,一个根在-5和-4之间,一个在2和3之间。
3、探求其解的十分位。
x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
x
2.1
2.2
2.3
2.4
y
-1.39
-0.76
-0.11
0.56
∴ 方程的两个近似根为x1≈-4.3,x2≈2.3。
基本步骤:
1、画出函数的图象;
2、根据图象确定抛物线
与x轴的交点分别在哪两
个相邻的整数之间;
3、利用计算器探索其解
的十分位数字,从而确定
方程的近似根。
1. 汽车刹车后的距离S(单位:m)与行驶时间t(单位为:s)的函数关系式S=15t-6t2,汽车刹车后停下来行驶5米,求汽车刹车后停下来的时间是多少?
解:由函数关系可得:
5 =15t-6t2
解方程得
x1≈0.98
x2≈28.75(不符合实际舍去)
所以汽车刹车后停下来的时间为0.98s.
2. 一个滑雪者从85m长的山坡滑下,滑行的距离为S(单位:m)与滑行的时间t(单位:s)的函数关系式是S=1.8t+0.064t2,他通过这段山坡需要多长时间?
解:由函数关系可得:
85 =1.8t+0.064t2
解方程得
t1=25
t2 = -53.125(不符合实际舍去)
他通过这段山坡需要25秒的时间
向上
向下
同号
<
=
异号
>
问题1. 如何由二次函数
y=ax2 +bx+c的图象确定a、b、c及△的符号?
(1)a的符号由抛物线___________确定;
(2)c的符号由抛物线___________确定;
(3)b的符号由抛物线___________确定;
(4)b2 -4ac的符号由抛物线______确定.
知识点一 二次函数y=ax2+bx+c与字母系数之间的关系
C
D
D
知识点一 二次函数y=ax2+bx+c与字母系数之间的关系
B
知识点一 二次函数y=ax2+bx+c与字母系数之间的关系
例1:已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )
A. ac<0 B. a﹣b+c>0
C. b=﹣4a
D.关于x的方程ax2+bx+c=0的
根是x1=﹣1,x2=5
解析:
B
解析:
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
A.该二次函数开口向下,则a<0;抛物线交y轴于正半轴,则c>0;所以ac<0,正确;;
解:
B.由于抛物线过(﹣1,0),则有:a﹣b+c=0,错误;
C.由图象知:抛物线的对称轴为x=2,即b=﹣4a,正确;
D.抛物线与x轴的交点为(﹣1,0),(5,0);故方程ax2+bx+c=0的根是x1=﹣1,x2=5,正确;故选B.
例2:抛物线y=ax2+bx+c在x轴的下方,则所要满足的条件是( )
A、a<0,b2﹣4ac<0 B、a<0,b2﹣4ac>0
C、a>0,b2﹣4ac<0 D、a>0,b2﹣4ac>0
解析:
抛物线在x轴下方,即可知开口向下,a<0,且与x轴没有交点,△<0.
解:
∵抛物线y=ax2+bx+c在x轴的下方,
∴由二次函数图象与系数关系知a<0,且与x轴没有交点,
即所对应二次方程没有解,
∴△=b2﹣4ac<0,
故选A.
A
例3:如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,
x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①abc>0; ②4a﹣2b+c<0;
③2a﹣b<0; ④b2+8a>4ac.
其中正确的有( )
解析:
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:
②当x=-2时,y=4a-2b+c<0,正确;
D
④∵y原点>2,a<0,∴4ac﹣b2<8a,即b2+8a>4ac,正确.选D。
①由图象可知a<0,c>0,- <0,∴b<0,∴abc>0,正确;
③根据题意得,对称轴-1<- <0,∴2a-b<0,正确;
例4:根据下列表格的对应值:
解析:
根据表格知道8<x<12,y随x的增大而增大,而﹣0.38<0<1.2,由此即可推出方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围.
解:
依题意得当8<x<12,y随x的增大而增大,
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A、8<x<9 B、9<x<10
C、10<x<11 D、11<x<12
而﹣0.38<0<1.2,
∴方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是10<x<11.故选C.
C
C
答案不唯一如:y=-x2+5等.
解:
(1)c=1.
(2)由图象过(0,1),A(1,0),得a+b+1=0,
故b=-a-1,由b2-4ac>0,
得(-a-1)2-4a>0即(a-1)2>0,
故a≠1又a>0所以a的取值范围是a>0且a≠1.
二次函数y=ax2 +bx+c的图象与字母系数a,b,c之间的关系:
1.当a>0时开口向上,当a<0时开口向下.
2.若对称轴在y轴的左边,则a,b同号.
若对称轴在y轴的右边,则a,b异号.
3.若抛物线与y轴的正半轴相交,则c>0,若抛物线与y轴的负半轴相交,则c<0,若抛物线经过原点则c=0 .
别式:
b2-4ac
二次函数
y=ax2+bx+c
(a≠0)
图象
一元二次方程ax2+bx+c=0
(a≠0)的根
x
y
O
与x轴有两个不
同的交点
(x1,0)
(x2,0)
有两个不同的解x=x1,x=x2
b2-4ac>0
x
y
O
与x轴有唯一个
交点
有两个相等的解
x1=x2=
b2-4ac=0
x
y
O
与x轴没有
交点
没有实数根
b2-4ac<0
由上面的结论,我们可以利用二次函数的图象求一元二次方程的根.由于作图或观察可能存在误差,由图象将得的根,一般是近似的.
例 利用函数图象求方程x2-2x-2=0 的实数根.
解:作y = x2-2x-2的图象,它与x轴的公共点的横坐标大约
是-0.7,2.7.
所以方程x2-2x-2=0的实数根为
x1≈-0.7,x2≈2.7
-2
2
2
4
6
4
-4
8
-2
-4
y = x2-2x-2
( 2.7, 0 )
(-0.7, 0 )
【例】你能利用二次函数的图象估计一元二次方程
的两根吗?其基本步骤是什么?
解:1、画出函数的图象。
2、由图象可知方程有两个根,一个根在-5和-4之间,一个在2和3之间。
3、探求其解的十分位。
x
-4.1
-4.2
-4.3
-4.4
y
-1.39
-0.76
-0.11
0.56
x
2.1
2.2
2.3
2.4
y
-1.39
-0.76
-0.11
0.56
∴ 方程的两个近似根为x1≈-4.3,x2≈2.3。
基本步骤:
1、画出函数的图象;
2、根据图象确定抛物线
与x轴的交点分别在哪两
个相邻的整数之间;
3、利用计算器探索其解
的十分位数字,从而确定
方程的近似根。
1. 汽车刹车后的距离S(单位:m)与行驶时间t(单位为:s)的函数关系式S=15t-6t2,汽车刹车后停下来行驶5米,求汽车刹车后停下来的时间是多少?
解:由函数关系可得:
5 =15t-6t2
解方程得
x1≈0.98
x2≈28.75(不符合实际舍去)
所以汽车刹车后停下来的时间为0.98s.
2. 一个滑雪者从85m长的山坡滑下,滑行的距离为S(单位:m)与滑行的时间t(单位:s)的函数关系式是S=1.8t+0.064t2,他通过这段山坡需要多长时间?
解:由函数关系可得:
85 =1.8t+0.064t2
解方程得
t1=25
t2 = -53.125(不符合实际舍去)
他通过这段山坡需要25秒的时间
向上
向下
同号
<
=
异号
>
问题1. 如何由二次函数
y=ax2 +bx+c的图象确定a、b、c及△的符号?
(1)a的符号由抛物线___________确定;
(2)c的符号由抛物线___________确定;
(3)b的符号由抛物线___________确定;
(4)b2 -4ac的符号由抛物线______确定.
知识点一 二次函数y=ax2+bx+c与字母系数之间的关系
C
D
D
知识点一 二次函数y=ax2+bx+c与字母系数之间的关系
B
知识点一 二次函数y=ax2+bx+c与字母系数之间的关系
例1:已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )
A. ac<0 B. a﹣b+c>0
C. b=﹣4a
D.关于x的方程ax2+bx+c=0的
根是x1=﹣1,x2=5
解析:
B
解析:
由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
A.该二次函数开口向下,则a<0;抛物线交y轴于正半轴,则c>0;所以ac<0,正确;;
解:
B.由于抛物线过(﹣1,0),则有:a﹣b+c=0,错误;
C.由图象知:抛物线的对称轴为x=2,即b=﹣4a,正确;
D.抛物线与x轴的交点为(﹣1,0),(5,0);故方程ax2+bx+c=0的根是x1=﹣1,x2=5,正确;故选B.
例2:抛物线y=ax2+bx+c在x轴的下方,则所要满足的条件是( )
A、a<0,b2﹣4ac<0 B、a<0,b2﹣4ac>0
C、a>0,b2﹣4ac<0 D、a>0,b2﹣4ac>0
解析:
抛物线在x轴下方,即可知开口向下,a<0,且与x轴没有交点,△<0.
解:
∵抛物线y=ax2+bx+c在x轴的下方,
∴由二次函数图象与系数关系知a<0,且与x轴没有交点,
即所对应二次方程没有解,
∴△=b2﹣4ac<0,
故选A.
A
例3:如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1,
x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①abc>0; ②4a﹣2b+c<0;
③2a﹣b<0; ④b2+8a>4ac.
其中正确的有( )
解析:
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:
②当x=-2时,y=4a-2b+c<0,正确;
D
④∵y原点>2,a<0,∴4ac﹣b2<8a,即b2+8a>4ac,正确.选D。
①由图象可知a<0,c>0,- <0,∴b<0,∴abc>0,正确;
③根据题意得,对称轴-1<- <0,∴2a-b<0,正确;
例4:根据下列表格的对应值:
解析:
根据表格知道8<x<12,y随x的增大而增大,而﹣0.38<0<1.2,由此即可推出方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围.
解:
依题意得当8<x<12,y随x的增大而增大,
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A、8<x<9 B、9<x<10
C、10<x<11 D、11<x<12
而﹣0.38<0<1.2,
∴方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是10<x<11.故选C.
C
C
答案不唯一如:y=-x2+5等.
解:
(1)c=1.
(2)由图象过(0,1),A(1,0),得a+b+1=0,
故b=-a-1,由b2-4ac>0,
得(-a-1)2-4a>0即(a-1)2>0,
故a≠1又a>0所以a的取值范围是a>0且a≠1.
二次函数y=ax2 +bx+c的图象与字母系数a,b,c之间的关系:
1.当a>0时开口向上,当a<0时开口向下.
2.若对称轴在y轴的左边,则a,b同号.
若对称轴在y轴的右边,则a,b异号.
3.若抛物线与y轴的正半轴相交,则c>0,若抛物线与y轴的负半轴相交,则c<0,若抛物线经过原点则c=0 .
同课章节目录
