2020-2021学年人教版数学九年级上册22.2二次函数与一元二次方程课件(19张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学九年级上册22.2二次函数与一元二次方程课件(19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 21:42:53 | ||
图片预览


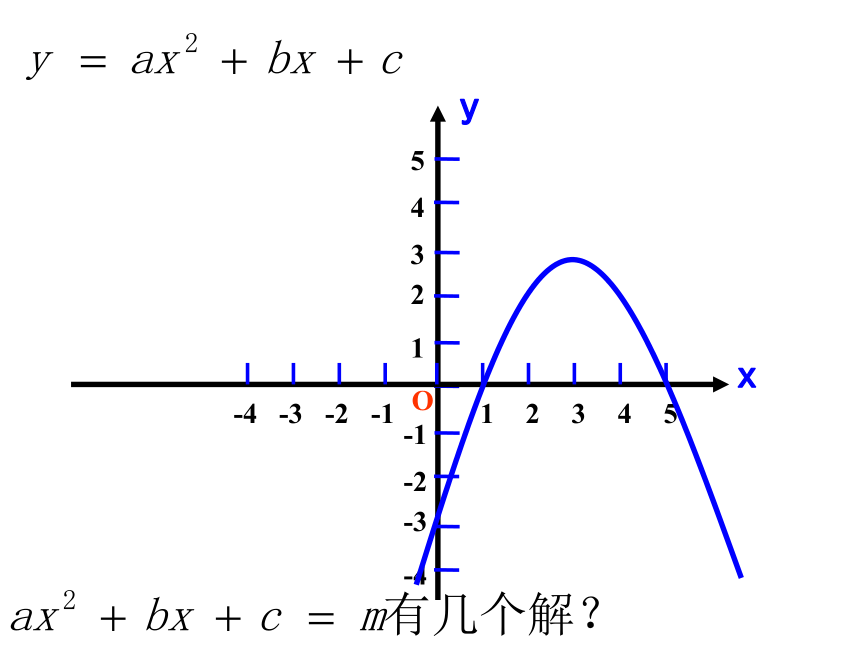


文档简介
22.2 二次函数与一元二次方程
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
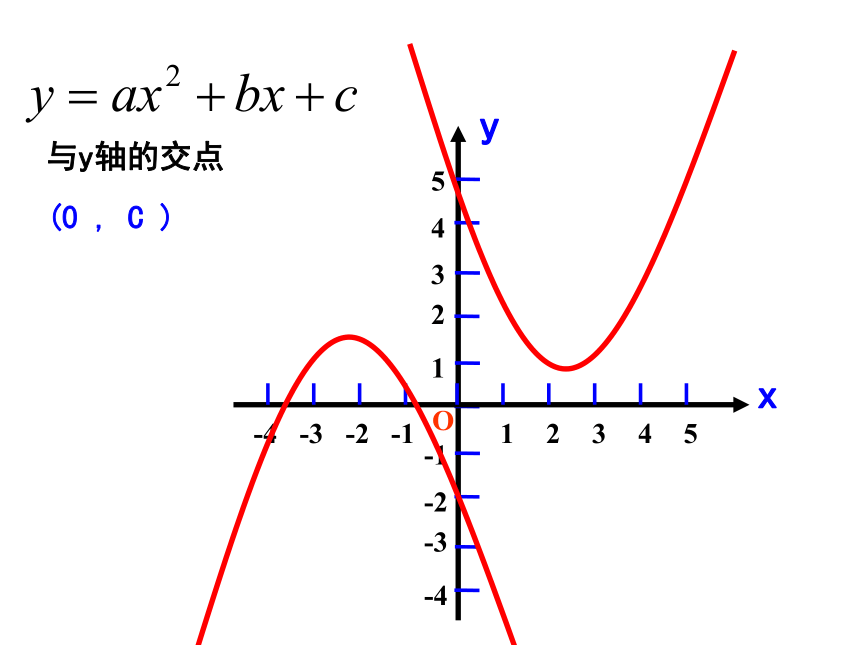
与y轴的交点
(0 , C )
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
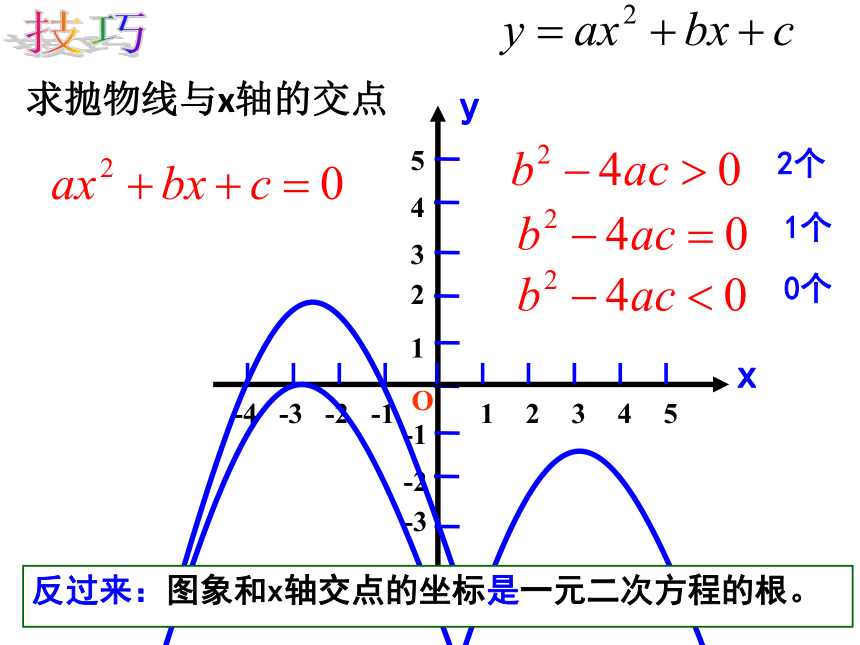
求抛物线与x轴的交点
2个
1个
0个
反过来:图象和x轴交点的坐标是一元二次方程的根。
y=ax2+bx+c和x轴交点
ax2+bx+c=0
b2-4ac
有两个交点
有两个不相等实数根
b2-4ac > 0
有一个交点
有两个相等实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
一元二次方程ax2+bx+c=0的根 就是
二次函数y=ax2+bx+c图象与x轴交点的横坐标
六、二次函数与一元二次方程的关系
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
1.抛物线y=-3x2-x+2与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
2.如图,已知抛物线与x轴的一个交点A(2,0),对称轴是x=-1,则该抛物线与x轴的另一个交点的坐标是( )
A.(-2,0) B.(-3,0)
C.(-4,0) D.(-5,0)
3.抛物线y=x2+6x+m与x轴只有一个公共点,则m的值为______.
是____
1 .
2.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=__.
16
且k≠0
二次函数与一元二次方程关系
例如,已知二次函数y = -x2+4x的值为3,求自变量x的值,可以解一元二次方程-x2+4x=3
反过来,解方程x2-4x+3=0 又可以看作已知二次函数 y = x2-4x+3 的值为0,求自变量x的值.
图象法解一元二次方程
三
例 利用函数图象求方程x2-2x-2=0的实数根(精确到0.1).
-2
2
2
4
6
4
-4
8
-2
-4
y = x2-2x-2
解:作y=x2-2x-2的图象(如右图所示),它与x轴的公共点的横坐标大约是-0.7,2.7.
所以方程x2-2x-2=0的实数根为
x1≈-0.7,x2≈2.7.
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x的范围是( )
A. 3< x < 3.23 B. 3.23 < x < 3.24
C. 3.24 x
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
2.根据下列表格的对应值:
3.二次函数y=x2-x-2的图象如图所示,则函数值y<0时x的取值范围是_______
y>4
x2-x-2>4
5. 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:h=20t-5t2,考虑以下问题:
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
O
h
t
15
1
3
∴当球飞行1s或3s时,它的高度为15m.
解析:解方程 15=20t-5t2,
t2-4t+3=0,
t1=1,t2=3.
你能结合上图,指出为什么在两个时间求的高度为15m吗?
h=20t-5t2
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
你能结合图形指出为什么只在一个时间球的高度为20m?
O
h
t
20
4
解方程:
20=20t-5t2,
t2-4t+4=0,
t1=t2=2.
当球飞行2秒时,它的高度为20米.
h=20t-5t2
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
O
h
t
你能结合图形指出为什么球不能达到20.5m的高度?
20.5
解方程:
20.5=20t-5t2,
t2-4t+4.1=0,
因为(-4)2-4 ×4.1<0,所以方程无解.
即球的飞行高度达不到20.5米.
h=20t-5t2
(4)球从飞出到落地要用多少时间?
O
h
t
0=20t-5t2,
t2-4t=0,
t1=0,t2=4.
当球飞行0秒和4秒时,它的高度为0米.
即0秒时球地面飞出,4秒时球落回地面.
h=20t-5t2
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
与y轴的交点
(0 , C )
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
求抛物线与x轴的交点
2个
1个
0个
反过来:图象和x轴交点的坐标是一元二次方程的根。
y=ax2+bx+c和x轴交点
ax2+bx+c=0
b2-4ac
有两个交点
有两个不相等实数根
b2-4ac > 0
有一个交点
有两个相等实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
一元二次方程ax2+bx+c=0的根 就是
二次函数y=ax2+bx+c图象与x轴交点的横坐标
六、二次函数与一元二次方程的关系
3
1
4
2
5
-2
-4
-1
-3
O
1
2
3
4
5
-4
-3
-2
-1
y
x
1.抛物线y=-3x2-x+2与坐标轴的交点个数是( )
A.3 B.2 C.1 D.0
2.如图,已知抛物线与x轴的一个交点A(2,0),对称轴是x=-1,则该抛物线与x轴的另一个交点的坐标是( )
A.(-2,0) B.(-3,0)
C.(-4,0) D.(-5,0)
3.抛物线y=x2+6x+m与x轴只有一个公共点,则m的值为______.
是____
1 .
2.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,则c=__.
16
且k≠0
二次函数与一元二次方程关系
例如,已知二次函数y = -x2+4x的值为3,求自变量x的值,可以解一元二次方程-x2+4x=3
反过来,解方程x2-4x+3=0 又可以看作已知二次函数 y = x2-4x+3 的值为0,求自变量x的值.
图象法解一元二次方程
三
例 利用函数图象求方程x2-2x-2=0的实数根(精确到0.1).
-2
2
2
4
6
4
-4
8
-2
-4
y = x2-2x-2
解:作y=x2-2x-2的图象(如右图所示),它与x轴的公共点的横坐标大约是-0.7,2.7.
所以方程x2-2x-2=0的实数根为
x1≈-0.7,x2≈2.7.
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x的范围是( )
A. 3< x < 3.23 B. 3.23 < x < 3.24
C. 3.24
3.23
3.24
3.25
3.26
y=ax2+bx+c
-0.06
-0.02
0.03
0.09
C
2.根据下列表格的对应值:
3.二次函数y=x2-x-2的图象如图所示,则函数值y<0时x的取值范围是_______
y>4
x2-x-2>4
5. 如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系:h=20t-5t2,考虑以下问题:
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
O
h
t
15
1
3
∴当球飞行1s或3s时,它的高度为15m.
解析:解方程 15=20t-5t2,
t2-4t+3=0,
t1=1,t2=3.
你能结合上图,指出为什么在两个时间求的高度为15m吗?
h=20t-5t2
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
你能结合图形指出为什么只在一个时间球的高度为20m?
O
h
t
20
4
解方程:
20=20t-5t2,
t2-4t+4=0,
t1=t2=2.
当球飞行2秒时,它的高度为20米.
h=20t-5t2
(3)球的飞行高度能否达到20.5m?如果能,需要多少飞行时间?
O
h
t
你能结合图形指出为什么球不能达到20.5m的高度?
20.5
解方程:
20.5=20t-5t2,
t2-4t+4.1=0,
因为(-4)2-4 ×4.1<0,所以方程无解.
即球的飞行高度达不到20.5米.
h=20t-5t2
(4)球从飞出到落地要用多少时间?
O
h
t
0=20t-5t2,
t2-4t=0,
t1=0,t2=4.
当球飞行0秒和4秒时,它的高度为0米.
即0秒时球地面飞出,4秒时球落回地面.
h=20t-5t2
同课章节目录
