人教版数学九年级上册第二十二章 二次函数22.2二次函数与一元二次方程课件PPT
文档属性
| 名称 | 人教版数学九年级上册第二十二章 二次函数22.2二次函数与一元二次方程课件PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览





文档简介
1、ax2+bx+c=0的根的情况可由___________确定。
b2-4ac>0 ______________
b2-4ac=0 ____________
b2-4ac<0 _____________
2、回顾一次函数与一元一次方程的关系如右图,因为直线y=x-2
与x轴的交点坐标为(__,0),所以方程x-2=0的解是____
3、二次函数y=x2-2x-3图像如图所示,你能根据图像
回答下列问题吗?
(1)x为何时,y=0?
(2)你能从图像上求出方程x2-2x-3=0的根吗?
(3)二次函数y=x2-2x-3与方程x2-2x-3=0之间有何关系?
y
0
x
15
y=15
1
3
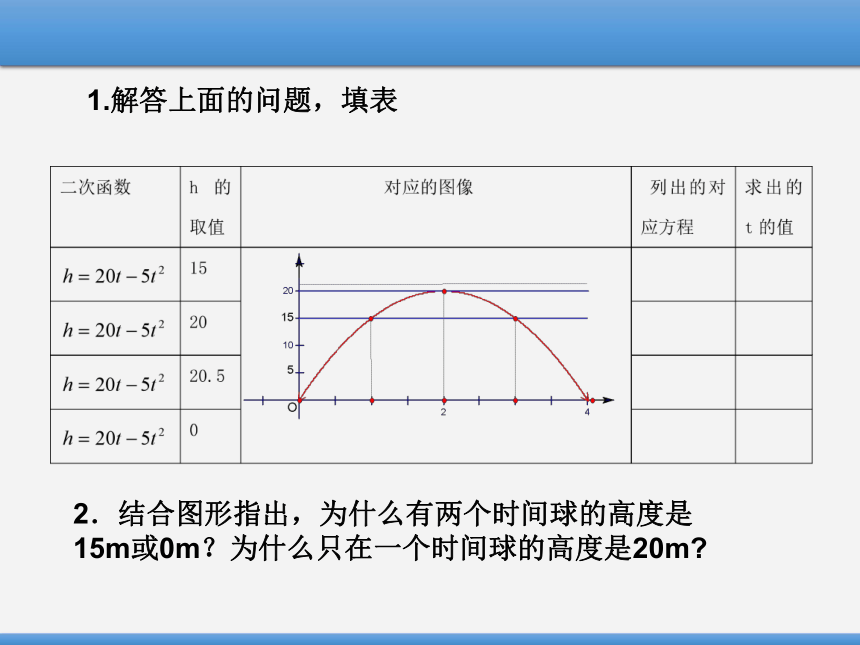
1.解答上面的问题,填表
2.结合图形指出,为什么有两个时间球的高度是15m或0m?为什么只在一个时间球的高度是20m?
当二次函数 y=ax2+bx+c(a≠0),给定y的值
时,则二次函数可转化为一元二次方程。
二次函数与一元二次方程有如下关系:
(1)二次函数y=ax2+bx+c当函数值y为某一确定值m时,对应自变量x的值,就是方程ax2+bx+c=m________;
(2)特别的当y=0时,对应自变量x的值就是方程ax2+bx+c=0的_______。
以上关系,反之也成立。
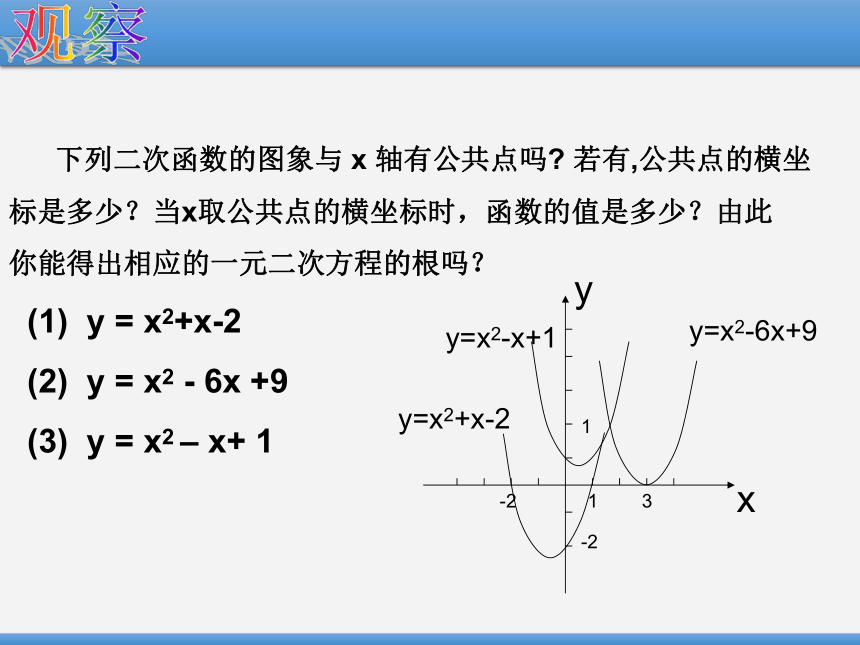
下列二次函数的图象与 x 轴有公共点吗? 若有,公共点的横坐
标是多少?当x取公共点的横坐标时,函数的值是多少?由此
你能得出相应的一元二次方程的根吗?
(1) y = x2+x-2
(2) y = x2 - 6x +9
(3) y = x2 – x+ 1
y
x
y=x2-6x+9
y=x2-x+1
y=x2+x-2
1
3
-2
-2
1
二次函数y=ax2+bx+c的图象和x轴公共点的横坐
标与一元二次方程ax2+bx+c=0的根有什么关系?
如果抛物线y=ax2+bx+c与x轴有公共点,公
共点的横坐标是x0,那么当x=x0时,函数的值
是0,因此x=x0就是方程ax2+bx+c=0的一个根。
二次函数y=ax2+bx+c的图象和x轴的位置
关系有三种情况:
(1)有两个公共点
(2)有一个公共点
(3)没有公共点
b2 – 4ac > 0
b2 – 4ac= 0
b2 – 4ac< 0
若抛物线y=ax2+bx+c与x轴有公共点,
则b2 – 4ac
≥0
同时也对应着一元二次方程根的三种情况:有两个不等的实数根,有两个相等的实数根,没有实数根
△>0
△=0
△<0
O
X
Y
二次函数y=ax2+bx+c的图象和x轴公共点
例1.已知抛物线y=x2- 2 x-3.
(1) 利用图像回答:
(Ⅰ)方程x2- 2 x-3=0的解是什么?
(Ⅱ)x取何值时y>0
(Ⅲ)x取何值时y<0
(2)在同一坐标系中作出y=x2-2x和y=3的图像,
(3)求出这两个图像交点的横坐标;
(4)比较(1)中(Ⅰ)和(3)的结果,能得到什么结论?
1.不与x轴相交的抛物线是( )
A y=2x2 – 3 B y= - 2 x2 + 3
C y= - x2 – 3x D y=-2(x+1)2 - 3
2.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴公共点情况是( )
A 无交点 B 只有一个交点
C 有两个交点 D不能确定
D
C
3.抛物线y=x2-3x-10 与y轴交于点 ,与x轴交
于点 .
归纳:一元二次方程ax2+bx+c=0的两个根为x1,x2 ,
则抛物线 y=ax2+bx+c与x轴的公共点坐标是
(x1,0),(x2,0)
(0,-10)
4.一元二次方程 x2+5x-14 = 0 的两个根是 x1= 2 ,
x2= -7 , 那么二次函数 y= x2+5x-14与x轴的交点坐
标是 .
(-2 ,0)和(5,0)
(2,0)和( -7,0)
5.如果关于x的一元二次方程 x2-2x+m=0有两个相
等的实数根,则m=__,此时抛物线 y=x2-2x+m
与x轴有__个公共点.
6.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,
则c=__.
1
1
16
7.如图,抛物线y=ax2+bx+c的对称轴是直线 x=-1,由图象知,关于x的方程ax2+bx+c=0的两个根分别是x1=1.3 ,x2=___
-3.3
x
o
y
X=-1
3
-1
1.3
.
点拨:抛物线与x轴的两个公共点关于x轴对称。
通过本节课的学习,你有哪些收获?
还有什么疑惑?
b2-4ac>0 ______________
b2-4ac=0 ____________
b2-4ac<0 _____________
2、回顾一次函数与一元一次方程的关系如右图,因为直线y=x-2
与x轴的交点坐标为(__,0),所以方程x-2=0的解是____
3、二次函数y=x2-2x-3图像如图所示,你能根据图像
回答下列问题吗?
(1)x为何时,y=0?
(2)你能从图像上求出方程x2-2x-3=0的根吗?
(3)二次函数y=x2-2x-3与方程x2-2x-3=0之间有何关系?
y
0
x
15
y=15
1
3
1.解答上面的问题,填表
2.结合图形指出,为什么有两个时间球的高度是15m或0m?为什么只在一个时间球的高度是20m?
当二次函数 y=ax2+bx+c(a≠0),给定y的值
时,则二次函数可转化为一元二次方程。
二次函数与一元二次方程有如下关系:
(1)二次函数y=ax2+bx+c当函数值y为某一确定值m时,对应自变量x的值,就是方程ax2+bx+c=m________;
(2)特别的当y=0时,对应自变量x的值就是方程ax2+bx+c=0的_______。
以上关系,反之也成立。
下列二次函数的图象与 x 轴有公共点吗? 若有,公共点的横坐
标是多少?当x取公共点的横坐标时,函数的值是多少?由此
你能得出相应的一元二次方程的根吗?
(1) y = x2+x-2
(2) y = x2 - 6x +9
(3) y = x2 – x+ 1
y
x
y=x2-6x+9
y=x2-x+1
y=x2+x-2
1
3
-2
-2
1
二次函数y=ax2+bx+c的图象和x轴公共点的横坐
标与一元二次方程ax2+bx+c=0的根有什么关系?
如果抛物线y=ax2+bx+c与x轴有公共点,公
共点的横坐标是x0,那么当x=x0时,函数的值
是0,因此x=x0就是方程ax2+bx+c=0的一个根。
二次函数y=ax2+bx+c的图象和x轴的位置
关系有三种情况:
(1)有两个公共点
(2)有一个公共点
(3)没有公共点
b2 – 4ac > 0
b2 – 4ac= 0
b2 – 4ac< 0
若抛物线y=ax2+bx+c与x轴有公共点,
则b2 – 4ac
≥0
同时也对应着一元二次方程根的三种情况:有两个不等的实数根,有两个相等的实数根,没有实数根
△>0
△=0
△<0
O
X
Y
二次函数y=ax2+bx+c的图象和x轴公共点
例1.已知抛物线y=x2- 2 x-3.
(1) 利用图像回答:
(Ⅰ)方程x2- 2 x-3=0的解是什么?
(Ⅱ)x取何值时y>0
(Ⅲ)x取何值时y<0
(2)在同一坐标系中作出y=x2-2x和y=3的图像,
(3)求出这两个图像交点的横坐标;
(4)比较(1)中(Ⅰ)和(3)的结果,能得到什么结论?
1.不与x轴相交的抛物线是( )
A y=2x2 – 3 B y= - 2 x2 + 3
C y= - x2 – 3x D y=-2(x+1)2 - 3
2.若抛物线y=ax2+bx+c,当 a>0,c<0时,图象与x轴公共点情况是( )
A 无交点 B 只有一个交点
C 有两个交点 D不能确定
D
C
3.抛物线y=x2-3x-10 与y轴交于点 ,与x轴交
于点 .
归纳:一元二次方程ax2+bx+c=0的两个根为x1,x2 ,
则抛物线 y=ax2+bx+c与x轴的公共点坐标是
(x1,0),(x2,0)
(0,-10)
4.一元二次方程 x2+5x-14 = 0 的两个根是 x1= 2 ,
x2= -7 , 那么二次函数 y= x2+5x-14与x轴的交点坐
标是 .
(-2 ,0)和(5,0)
(2,0)和( -7,0)
5.如果关于x的一元二次方程 x2-2x+m=0有两个相
等的实数根,则m=__,此时抛物线 y=x2-2x+m
与x轴有__个公共点.
6.已知抛物线 y=x2 – 8x +c的顶点在 x轴上,
则c=__.
1
1
16
7.如图,抛物线y=ax2+bx+c的对称轴是直线 x=-1,由图象知,关于x的方程ax2+bx+c=0的两个根分别是x1=1.3 ,x2=___
-3.3
x
o
y
X=-1
3
-1
1.3
.
点拨:抛物线与x轴的两个公共点关于x轴对称。
通过本节课的学习,你有哪些收获?
还有什么疑惑?
同课章节目录
