2020-2021学年人教版数学九年级上册22.2二次函数中的符号问题与求解析式课件(共24张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学九年级上册22.2二次函数中的符号问题与求解析式课件(共24张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览





文档简介
学习目标
1、能根据函数图像确定a、b、c以及△的符号。
2、经历探索二次函数 y=ax2+bx+cy=a的a、b、c的符号过程,培
养学生观察能力和类比的数学思想。
3、培养学生勇于探索的精神,树立学习的自信心。
共23张
*
1、抛物线y=2x2-3x+5 的开口方向____,与y轴的交点坐标是___.
2、抛物线y=-2(x-3)2-6 的开口方向____,对称轴是( ),顶点坐标是( ),y随x的变化情况( )。
3、二次函数y=ax2+bx+c的对称轴( )。
向上
(0,5)
向下
x=3
3,-6)
当x<3时,y随x的增大而增大,当x>3时,y随x的增大而减小
x= -
4、抛物线y=ax2+bx+c的开口方向与什么有关?
5、抛物线y=ax2+bx+c与y轴的交点是 .
a>0时,开口向上;a<0时,开口向下。
(0, c)
共23张
*
4
-2
2
2
4
6
-4
8
10
-2
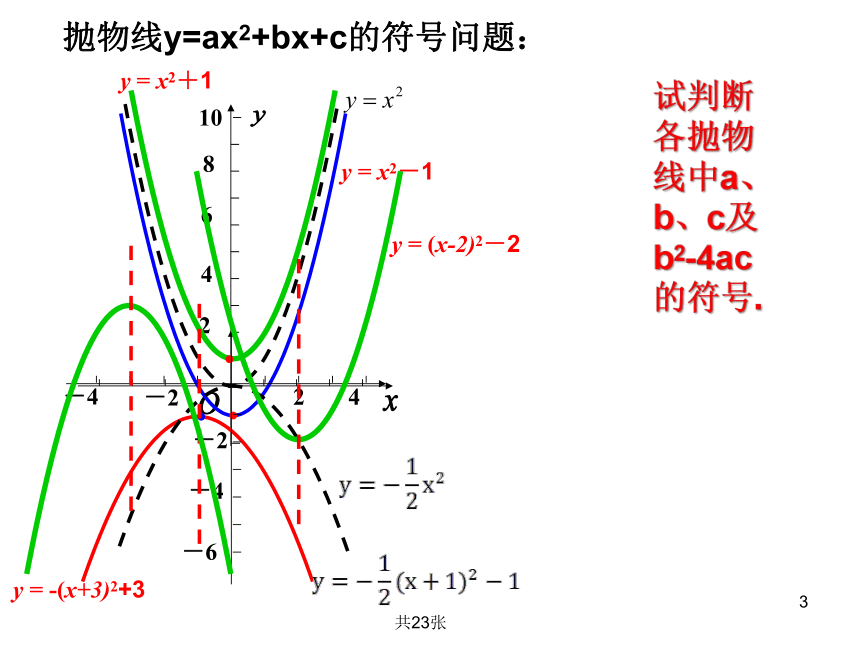
y = x2+1
y = x2-1
-4
-6
y = (x-2)2-2
y = -(x+3)2+3
抛物线y=ax2+bx+c的符号问题:
试判断各抛物线中a、b、c及b2-4ac的符号.
共23张
*
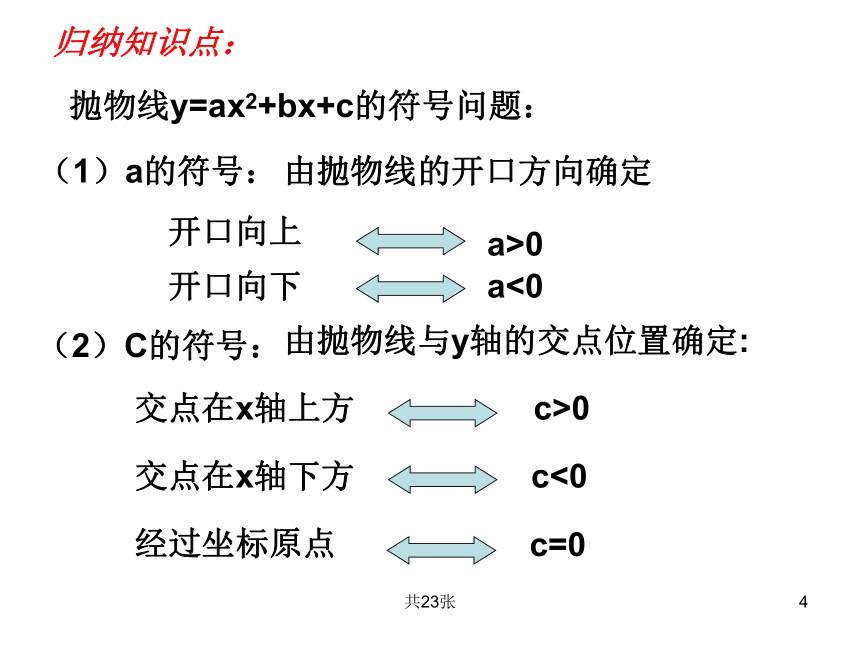
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定:
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
共23张
*
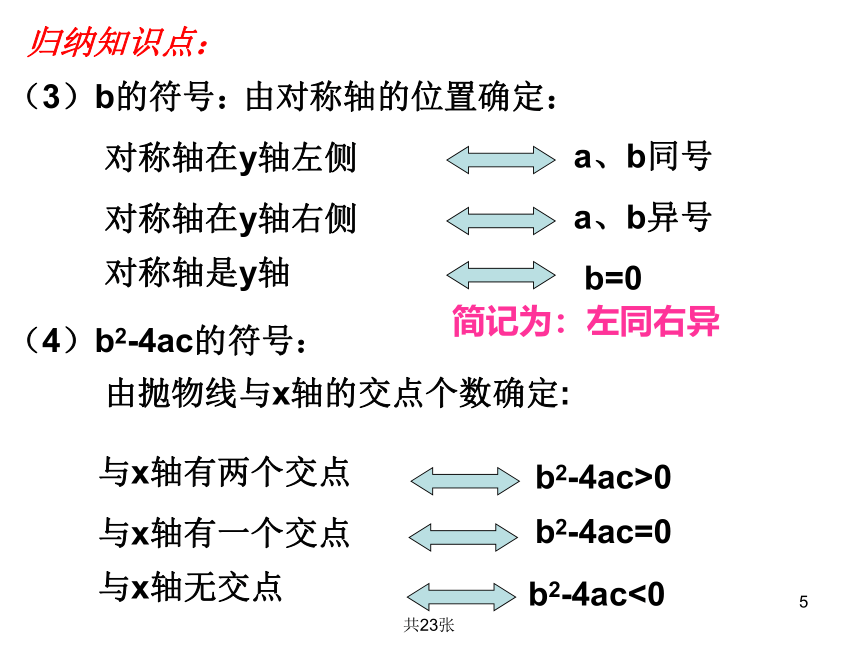
(3)b的符号:
由对称轴的位置确定:
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定:
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
归纳知识点:
简记为:左同右异
共23张
*
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(5)a+b+c的符号:
由x=1时抛物线上的点的位置确定
(6)a-b+c的符号:
由x=-1时抛物线上的点的位置确定
共23张
*
二次函数y=ax2+bx+c(a≠0)的系数a,b,c,△与
抛物线的关系
a
a,b
c
△
a决定开口方向:a>0时开口向上,
a<0时开口向下 ︳a︱越大开口越小。
a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴
c决定抛物线与y轴的交点:c>0时抛物线交于y轴的正半轴
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴
△决定抛物线与x轴的交点:△>0时抛物线与x轴有两个交点
△=0时抛物线与x轴有一个交点
△<0时抛物线于x轴没有交点
共23张
*
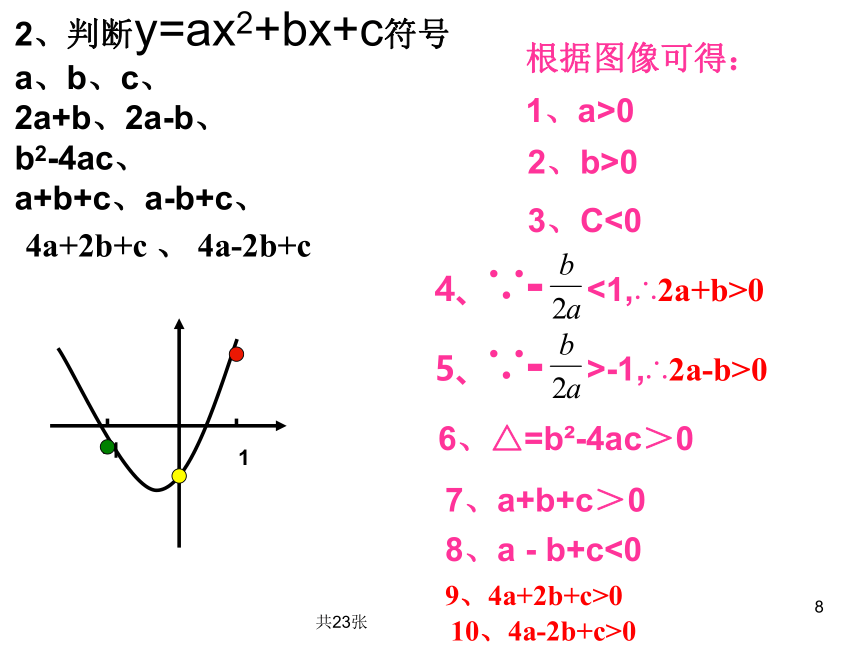
2、判断y=ax2+bx+c符号
a、b、c、
2a+b、2a-b、
b2-4ac、
a+b+c、a-b+c、
1
-1
根据图像可得:
1、a>0
2、b>0
3、C<0
4、∵- <1,∴2a+b>0
5、∵- >-1,∴2a-b>0
6、△=b?-4ac>0
7、a+b+c>0
8、a - b+c<0
4a+2b+c 、 4a-2b+c
9、4a+2b+c>0
10、4a-2b+c>0
共23张
*
a
b
c
2a+b
2a-b
b2-4ac
a+b+c
a-b+c
4a+2b+c
4a-2b+c
开口方向大小 向上a>0 向下a对称轴与y轴比较 左侧ab同号 右侧ab异号
与y轴交点 交于上半轴c>o 下半轴c<0
- 与1比较
- 与-1比较
与x轴交点个数
令x=1,看纵坐标
令x=-1,看纵坐标
令x=2,看纵坐标
令x=-2,看纵坐标
共23张
*
3、判断
y=ax2+bx+c符号
a 、 b 、 c
2a+b,2a-b,
b2-4ac
a+b+c
a-b+c
4a-2b+c
1
-1
根据图像可得:
1、a<0
2、b>0
3、C>0
4、∵- <1,∴2a+b<0
5、∵- >-1,∴2a-b<0
6、△=b?-4ac>0
7、a+b+c>0
8、a - b+c<0
9、4a-2b+c<0
共23张
*
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
根据图像可得:
1、a>0
2、b<0
3、- >0
4、△=b?-4ac>0
5、C>0
共23张
*
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
根据图像可得:
1、a>0,b>0
2、- <0
3、△=b?-4ac>0
4、C=0
共23张
*
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
根据图像可得:
1、a>0,b<0
4、C>0
2、- >0
3、△=b?-4ac=0
共23张
*
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
根据图像可得:
1、a>0,b=0
4、C=0
2、- =0
3、△=b?-4ac=0
共23张
*
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
根据图像可得:
1、a<0,b>0
4、C<0
2、- >0
3、△=b?-4ac<0
共23张
*
练一练:
1.已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )
A、第一象限 B、第二象限
C、第三象限 D、第四象限
x
o
y
D
根据图像可得:
1、a<0
2、- >0
3、△=b?-4ac>0
4、C>0
共23张
*
练一练:
2、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个
x
o
y
x=1
B
根据图像可得:
1、a<0
2、- =1
3、△=b?-4ac>0
4、C<0
5、当x=2时y<0,故4a+2b+c < 0
6、(a+c)2-b2=(a+b+c)(a-b+c),而a+b+c>0,a-b+c<0,故(a+c)2-b2<0
共23张
*
练一练:
3、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
C
根据图像可得:
1、a<0
2、- =-1
3、△=b?-4ac>0
4、C>0
共23张
*
4.(06.芜湖市)如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是 .
再想一想:
-2
设正方形的对角线长为2n,
根据图像可得:
∵A(0、2n)、B(-n、n)、
C(n、n)
∴n=a(±n)?+2n、c=2n,
∴a=- ,∴ac=2n*(- )
=-2
共23张
*
5.(06.浙江省)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.
(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答, 则只以第(2)问计分)
第(1)问:给出四个结论:
①a>0;② b>0;③c>0;④ a+b+c=0.其中正确结论的序号是 (答对得3分,少选、错选均不得分).
第(2)问:给出四个结论:
① abc<0;②2a+b>0;③a+c=1;④a>1.其中正确结论的序号是 (答对得5分,少选、错选均不得分).
x
y
O
1
-1
2
仔细想一想:
①④
② ③ ④
提示:
③
共23张
*
课堂小结
本节课你有哪些收获?
1、能根据函数图像确定a、b、c以及△的符号;
2、能确定对称轴的取值范围;
3、会判断特殊的式子的取值范围,如a+b+c、
a-b+c、2a+b、2a-b、4a+2b+c、4a-2b+c
等
共23张
*
2.若关于x的函数y=(a-2)x2-(2a-1)x+a的图象与坐标轴有两个交点,则a可取的值为 ;
1.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2 ≥y1时,x的取值范围是________;
4.已知抛物线y=ax2+bx+c (a<0)经过点(-1,0),
且满足4a+2b+c>0.以下结论:①a+b>0;②a+c>0;③-a+b+c>0;④b2-2ac>5a2.其中正确的个数有( )
(A)1个 (B)2个 (C)3个 (D)4个
布置作业
3、请你写出一个二次函数y=ax2+bx+c,使它同时具有如下性质:①图象关于直线x=1对称; ②当x=2时,y>0;③当x=-2时,y<0。 答:____________
共23张
*
5、二次函数y=ax2+bx+c的图象如图所示,那abc,b2-4ac,2a+b,a+b+c,a-b+c 这五个代数式中,值为正数的有( )
A.4个 B.3个
C.2个 D.1个
y
x
-1
1
6、根据下列表格中二次函数y=ax2+bx+c的自变量与函数值的对应值,判断方程ax2+bx+c =0
(a≠0, a, b, c为常数)的一个解的范围是( )
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
-0.03
-0.01
0.02
0.04
A.6.17< X <6.18 B.6.18< X <6.19
C.-0.01< X <0.02 D.6.19< X <6.20
共23张
*
1)因为抛物线y=ax2+bx+c(a<0)经过点(-1,0),
所以原式可化为a-b+c=0----①,
又因为4a+2b+c>0----②,
所以②-①得:3a+3b>0,
即a+b>0
(2)②+①×2得,6a+3c>0,
即2a+c>0,∴a+c>-a,∵a<0,∴-a>0 故a+c>0;
(4)∵过(-1,0),代入得a-b+c=0,
∴b2-2ac-5a2=(a+c)2-2ac-5a2=c2-4a2=(c+2a)(c-2a)
又∵4a+2b+c>0 4a+2(a+c)+c>0 即2a+c>0①
∵a<0 ∴c>0 则c-2a>0②
由①②知(c+2a)(c-2a)>0, 所以b2-2ac-5a2>0,即b2-2ac>5a2
综上可知正确的个数有4个
(3)因为4a+2b+c>0,可以看作y=ax2+bx+c(a<0)当x=2时的值大于0,草图为:
可见c>0,
∵a-b+c=0,
∴-a+b-c=0,
两边同时加2c得-a+b-c+2c=2c,
整理得-a+b+c=2c>0,
即-a+b+c>0;
故a+c>0;
共23张
*
1、能根据函数图像确定a、b、c以及△的符号。
2、经历探索二次函数 y=ax2+bx+cy=a的a、b、c的符号过程,培
养学生观察能力和类比的数学思想。
3、培养学生勇于探索的精神,树立学习的自信心。
共23张
*
1、抛物线y=2x2-3x+5 的开口方向____,与y轴的交点坐标是___.
2、抛物线y=-2(x-3)2-6 的开口方向____,对称轴是( ),顶点坐标是( ),y随x的变化情况( )。
3、二次函数y=ax2+bx+c的对称轴( )。
向上
(0,5)
向下
x=3
3,-6)
当x<3时,y随x的增大而增大,当x>3时,y随x的增大而减小
x= -
4、抛物线y=ax2+bx+c的开口方向与什么有关?
5、抛物线y=ax2+bx+c与y轴的交点是 .
a>0时,开口向上;a<0时,开口向下。
(0, c)
共23张
*
4
-2
2
2
4
6
-4
8
10
-2
y = x2+1
y = x2-1
-4
-6
y = (x-2)2-2
y = -(x+3)2+3
抛物线y=ax2+bx+c的符号问题:
试判断各抛物线中a、b、c及b2-4ac的符号.
共23张
*
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(1)a的符号:
由抛物线的开口方向确定
开口向上
a>0
开口向下
a<0
(2)C的符号:
由抛物线与y轴的交点位置确定:
交点在x轴上方
c>0
交点在x轴下方
c<0
经过坐标原点
c=0
共23张
*
(3)b的符号:
由对称轴的位置确定:
对称轴在y轴左侧
a、b同号
对称轴在y轴右侧
a、b异号
对称轴是y轴
b=0
(4)b2-4ac的符号:
由抛物线与x轴的交点个数确定:
与x轴有两个交点
b2-4ac>0
与x轴有一个交点
b2-4ac=0
与x轴无交点
b2-4ac<0
归纳知识点:
简记为:左同右异
共23张
*
归纳知识点:
抛物线y=ax2+bx+c的符号问题:
(5)a+b+c的符号:
由x=1时抛物线上的点的位置确定
(6)a-b+c的符号:
由x=-1时抛物线上的点的位置确定
共23张
*
二次函数y=ax2+bx+c(a≠0)的系数a,b,c,△与
抛物线的关系
a
a,b
c
△
a决定开口方向:a>0时开口向上,
a<0时开口向下 ︳a︱越大开口越小。
a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴
c决定抛物线与y轴的交点:c>0时抛物线交于y轴的正半轴
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴
△决定抛物线与x轴的交点:△>0时抛物线与x轴有两个交点
△=0时抛物线与x轴有一个交点
△<0时抛物线于x轴没有交点
共23张
*
2、判断y=ax2+bx+c符号
a、b、c、
2a+b、2a-b、
b2-4ac、
a+b+c、a-b+c、
1
-1
根据图像可得:
1、a>0
2、b>0
3、C<0
4、∵- <1,∴2a+b>0
5、∵- >-1,∴2a-b>0
6、△=b?-4ac>0
7、a+b+c>0
8、a - b+c<0
4a+2b+c 、 4a-2b+c
9、4a+2b+c>0
10、4a-2b+c>0
共23张
*
a
b
c
2a+b
2a-b
b2-4ac
a+b+c
a-b+c
4a+2b+c
4a-2b+c
开口方向大小 向上a>0 向下a
与y轴交点 交于上半轴c>o 下半轴c<0
- 与1比较
- 与-1比较
与x轴交点个数
令x=1,看纵坐标
令x=-1,看纵坐标
令x=2,看纵坐标
令x=-2,看纵坐标
共23张
*
3、判断
y=ax2+bx+c符号
a 、 b 、 c
2a+b,2a-b,
b2-4ac
a+b+c
a-b+c
4a-2b+c
1
-1
根据图像可得:
1、a<0
2、b>0
3、C>0
4、∵- <1,∴2a+b<0
5、∵- >-1,∴2a-b<0
6、△=b?-4ac>0
7、a+b+c>0
8、a - b+c<0
9、4a-2b+c<0
共23张
*
快速回答:
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
o
y
根据图像可得:
1、a>0
2、b<0
3、- >0
4、△=b?-4ac>0
5、C>0
共23张
*
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
根据图像可得:
1、a>0,b>0
2、- <0
3、△=b?-4ac>0
4、C=0
共23张
*
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
根据图像可得:
1、a>0,b<0
4、C>0
2、- >0
3、△=b?-4ac=0
共23张
*
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
根据图像可得:
1、a>0,b=0
4、C=0
2、- =0
3、△=b?-4ac=0
共23张
*
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
快速回答:
根据图像可得:
1、a<0,b>0
4、C<0
2、- >0
3、△=b?-4ac<0
共23张
*
练一练:
1.已知:二次函数y=ax2+bx+c的图象如图所示,则点M( ,a)在( )
A、第一象限 B、第二象限
C、第三象限 D、第四象限
x
o
y
D
根据图像可得:
1、a<0
2、- >0
3、△=b?-4ac>0
4、C>0
共23张
*
练一练:
2、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个
x
o
y
x=1
B
根据图像可得:
1、a<0
2、- =1
3、△=b?-4ac>0
4、C<0
5、当x=2时y<0,故4a+2b+c < 0
6、(a+c)2-b2=(a+b+c)(a-b+c),而a+b+c>0,a-b+c<0,故(a+c)2-b2<0
共23张
*
练一练:
3、已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
C
根据图像可得:
1、a<0
2、- =-1
3、△=b?-4ac>0
4、C>0
共23张
*
4.(06.芜湖市)如图,在平面直角坐标系中,二次函数y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C,则ac的值是 .
再想一想:
-2
设正方形的对角线长为2n,
根据图像可得:
∵A(0、2n)、B(-n、n)、
C(n、n)
∴n=a(±n)?+2n、c=2n,
∴a=- ,∴ac=2n*(- )
=-2
共23张
*
5.(06.浙江省)如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和(1,0),且与y轴相交于负半轴.
(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答, 则只以第(2)问计分)
第(1)问:给出四个结论:
①a>0;② b>0;③c>0;④ a+b+c=0.其中正确结论的序号是 (答对得3分,少选、错选均不得分).
第(2)问:给出四个结论:
① abc<0;②2a+b>0;③a+c=1;④a>1.其中正确结论的序号是 (答对得5分,少选、错选均不得分).
x
y
O
1
-1
2
仔细想一想:
①④
② ③ ④
提示:
③
共23张
*
课堂小结
本节课你有哪些收获?
1、能根据函数图像确定a、b、c以及△的符号;
2、能确定对称轴的取值范围;
3、会判断特殊的式子的取值范围,如a+b+c、
a-b+c、2a+b、2a-b、4a+2b+c、4a-2b+c
等
共23张
*
2.若关于x的函数y=(a-2)x2-(2a-1)x+a的图象与坐标轴有两个交点,则a可取的值为 ;
1.如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2 ≥y1时,x的取值范围是________;
4.已知抛物线y=ax2+bx+c (a<0)经过点(-1,0),
且满足4a+2b+c>0.以下结论:①a+b>0;②a+c>0;③-a+b+c>0;④b2-2ac>5a2.其中正确的个数有( )
(A)1个 (B)2个 (C)3个 (D)4个
布置作业
3、请你写出一个二次函数y=ax2+bx+c,使它同时具有如下性质:①图象关于直线x=1对称; ②当x=2时,y>0;③当x=-2时,y<0。 答:____________
共23张
*
5、二次函数y=ax2+bx+c的图象如图所示,那abc,b2-4ac,2a+b,a+b+c,a-b+c 这五个代数式中,值为正数的有( )
A.4个 B.3个
C.2个 D.1个
y
x
-1
1
6、根据下列表格中二次函数y=ax2+bx+c的自变量与函数值的对应值,判断方程ax2+bx+c =0
(a≠0, a, b, c为常数)的一个解的范围是( )
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
-0.03
-0.01
0.02
0.04
A.6.17< X <6.18 B.6.18< X <6.19
C.-0.01< X <0.02 D.6.19< X <6.20
共23张
*
1)因为抛物线y=ax2+bx+c(a<0)经过点(-1,0),
所以原式可化为a-b+c=0----①,
又因为4a+2b+c>0----②,
所以②-①得:3a+3b>0,
即a+b>0
(2)②+①×2得,6a+3c>0,
即2a+c>0,∴a+c>-a,∵a<0,∴-a>0 故a+c>0;
(4)∵过(-1,0),代入得a-b+c=0,
∴b2-2ac-5a2=(a+c)2-2ac-5a2=c2-4a2=(c+2a)(c-2a)
又∵4a+2b+c>0 4a+2(a+c)+c>0 即2a+c>0①
∵a<0 ∴c>0 则c-2a>0②
由①②知(c+2a)(c-2a)>0, 所以b2-2ac-5a2>0,即b2-2ac>5a2
综上可知正确的个数有4个
(3)因为4a+2b+c>0,可以看作y=ax2+bx+c(a<0)当x=2时的值大于0,草图为:
可见c>0,
∵a-b+c=0,
∴-a+b-c=0,
两边同时加2c得-a+b-c+2c=2c,
整理得-a+b+c=2c>0,
即-a+b+c>0;
故a+c>0;
共23张
*
同课章节目录
