2020-2021学年人教版数学九年级上册二次函数与一元二次方程-abc意义课件(共27张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学九年级上册二次函数与一元二次方程-abc意义课件(共27张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 843.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 19:38:05 | ||
图片预览




文档简介
二次函数与一元二次方程
a,b,c的符号意义
对于二次函数y=ax2+bx+c(a≠0):
1.求与y轴交点坐标,令 ,得
所以与y轴交点坐标 ;
若交于原点,则
2.求与x轴交点坐标,令
得方程ax2+bx+c=0,
它根的情况决定抛物线与x轴交点的个数。
对于二次函数y=ax2+bx+c(a≠0),Δ=b2-4ac。
当Δ>0时,抛物线与x轴有 个交点,这两个交点的横坐标是方程ax2+bx+c=0的两个不相等的根。
当Δ=0时,抛物线与x轴有 个交点。这时方程ax2+bx+c=0有两个 的根,此时这一个交点即为抛物线的顶点。
当Δ<0时,抛物线与x轴 交点。这时方程ax2+bx+c=0根的情况 。
两
一
无
没有实数根
相等
已知二次函数 y=kx2-7x-7的图象与x轴有交点,
则k的取值范围是 ( )
A、k≥
B、k≥
C、k>
D、k>
B
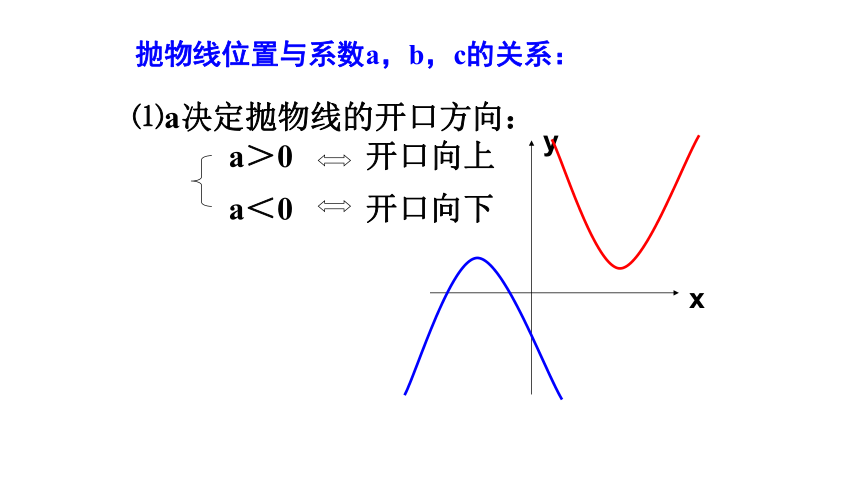
抛物线位置与系数a,b,c的关系:
⑴a决定抛物线的开口方向:
a>0 开口向上
a<0 开口向下
x
y
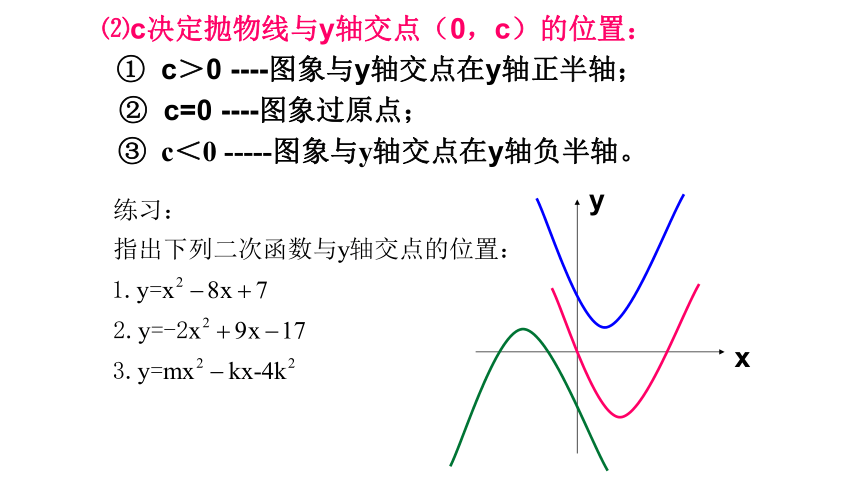
③??c<0 -----图象与y轴交点在y轴负半轴。
⑵c决定抛物线与y轴交点(0,c)的位置:
①??c>0 ----图象与y轴交点在y轴正半轴;
②??c=0 ----图象过原点;
x
y
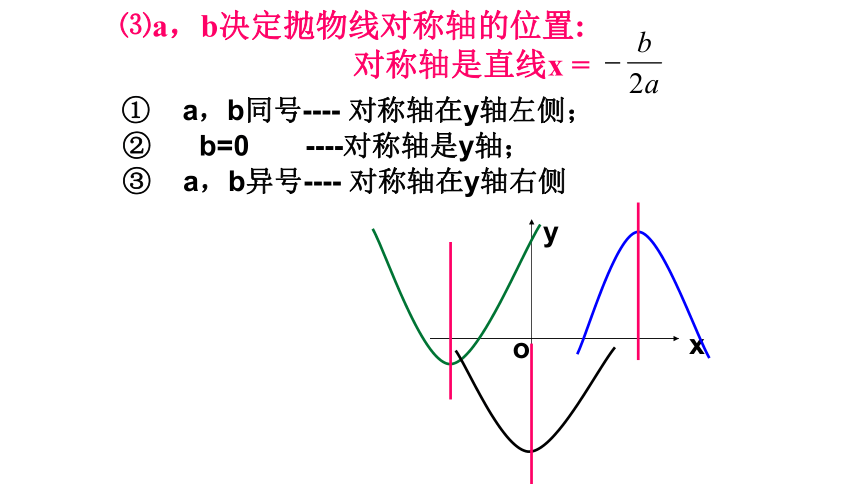
⑶a,b决定抛物线对称轴的位置:
对称轴是直线x =
①??? a,b同号---- 对称轴在y轴左侧;
②??? b=0 ----对称轴是y轴;
③ a,b异号---- 对称轴在y轴右侧
o
x
y
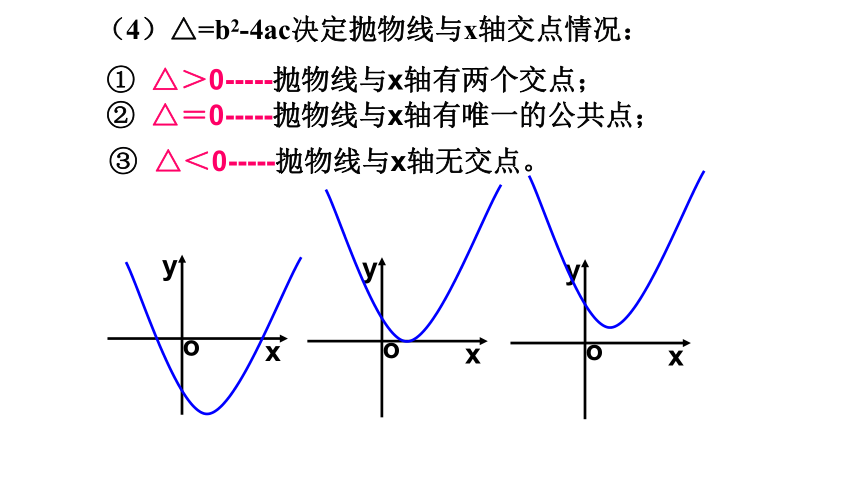
(4)△=b2-4ac决定抛物线与x轴交点情况:
y
o
x
y
o
x
y
o
x
①??△>0-----抛物线与x轴有两个交点;
②??△=0-----抛物线与x轴有唯一的公共点;
③? △<0-----抛物线与x轴无交点。
△=0--y≤0恒成立
△<0--y<0恒成立
△>0--y>0,<0,=0
y
o
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
x
△=0--y≥0恒成立
△<0--y>0恒成立
△>0--y>0,<0,=0
若抛物线
位于x轴上方,求m的取值范围.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
0
a>0,
b<0,
c>0,
△>0.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
0
△>0.
c=0,
a>0
b>0
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
a<0,
b<0,
c>0,
△>0.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
a>0,
b<0,
c>0,
△=0.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
a>0,
b=0,
c=0,
△=0.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
a<0,
b>0,
c<0,
△<0.
y
o
x
y
o
x
图1
图2
o
x
y
X=1
当x=1时,对应的纵坐标y的值
o
x
y
X=-1
当x=-1时,对应的纵坐标y的值
(5)已知y=ax2+bx+c的图象如图所示,
2a-b的符合 与对称轴x=-1有关
2a+b的符合 与对称轴x=1有关
0
-1
1
-2
y
o
x
-1
1
<
<
>
<
>
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;
③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
C
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中下不正确的是 ( )
A、abc>0
B、b2-4ac>0
C、2a+b>0
D、4a-2b+c<0
x
o
y
-1
1
D
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个
x
o
y
x=1
B
8、已知:一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系中的大致图象是图中的( )
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
C
练习
a,b,c的符号意义
对于二次函数y=ax2+bx+c(a≠0):
1.求与y轴交点坐标,令 ,得
所以与y轴交点坐标 ;
若交于原点,则
2.求与x轴交点坐标,令
得方程ax2+bx+c=0,
它根的情况决定抛物线与x轴交点的个数。
对于二次函数y=ax2+bx+c(a≠0),Δ=b2-4ac。
当Δ>0时,抛物线与x轴有 个交点,这两个交点的横坐标是方程ax2+bx+c=0的两个不相等的根。
当Δ=0时,抛物线与x轴有 个交点。这时方程ax2+bx+c=0有两个 的根,此时这一个交点即为抛物线的顶点。
当Δ<0时,抛物线与x轴 交点。这时方程ax2+bx+c=0根的情况 。
两
一
无
没有实数根
相等
已知二次函数 y=kx2-7x-7的图象与x轴有交点,
则k的取值范围是 ( )
A、k≥
B、k≥
C、k>
D、k>
B
抛物线位置与系数a,b,c的关系:
⑴a决定抛物线的开口方向:
a>0 开口向上
a<0 开口向下
x
y
③??c<0 -----图象与y轴交点在y轴负半轴。
⑵c决定抛物线与y轴交点(0,c)的位置:
①??c>0 ----图象与y轴交点在y轴正半轴;
②??c=0 ----图象过原点;
x
y
⑶a,b决定抛物线对称轴的位置:
对称轴是直线x =
①??? a,b同号---- 对称轴在y轴左侧;
②??? b=0 ----对称轴是y轴;
③ a,b异号---- 对称轴在y轴右侧
o
x
y
(4)△=b2-4ac决定抛物线与x轴交点情况:
y
o
x
y
o
x
y
o
x
①??△>0-----抛物线与x轴有两个交点;
②??△=0-----抛物线与x轴有唯一的公共点;
③? △<0-----抛物线与x轴无交点。
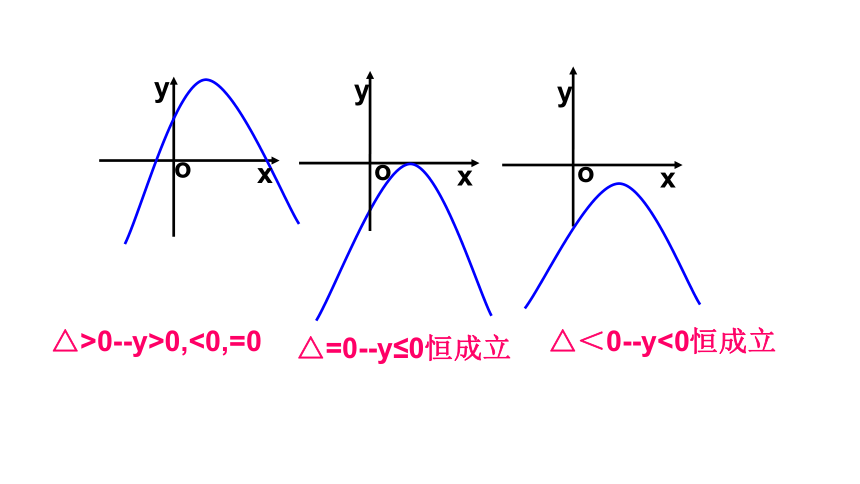
△=0--y≤0恒成立
△<0--y<0恒成立
△>0--y>0,<0,=0
y
o
x
y
o
x
y
o
x
y
o
x
y
o
x
y
o
x
△=0--y≥0恒成立
△<0--y>0恒成立
△>0--y>0,<0,=0
若抛物线
位于x轴上方,求m的取值范围.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
0
a>0,
b<0,
c>0,
△>0.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
0
△>0.
c=0,
a>0
b>0
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
a<0,
b<0,
c>0,
△>0.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
a>0,
b<0,
c>0,
△=0.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
a>0,
b=0,
c=0,
△=0.
抛物线y=ax2+bx+c如图所示,试确定a、b、c、△的符号:
x
y
o
a<0,
b>0,
c<0,
△<0.
y
o
x
y
o
x
图1
图2
o
x
y
X=1
当x=1时,对应的纵坐标y的值
o
x
y
X=-1
当x=-1时,对应的纵坐标y的值
(5)已知y=ax2+bx+c的图象如图所示,
2a-b的符合 与对称轴x=-1有关
2a+b的符合 与对称轴x=1有关
0
-1
1
-2
y
o
x
-1
1
<
<
>
<
>
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①abc>0;②b=2a;
③a+b+c<0;④a+b-c>0; ⑤a-b+c>0正确的个数是 ( )
A、2个 B、3个
C、4个 D、5个
x
o
y
-1
1
C
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中下不正确的是 ( )
A、abc>0
B、b2-4ac>0
C、2a+b>0
D、4a-2b+c<0
x
o
y
-1
1
D
已知:二次函数y=ax2+bx+c的图象如图所示,下列结论中:①b>0;②c<0;③4a+2b+c > 0;④(a+c)2<b2,其中正确的个数是 ( )
A、4个 B、3个
C、2个 D、1个
x
o
y
x=1
B
8、已知:一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系中的大致图象是图中的( )
x
y
o
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
(D)
C
练习
同课章节目录
