2020-2021学年人教版数学九年级上册二次函数与一元二次方程PPT课件 (2)(共25张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学九年级上册二次函数与一元二次方程PPT课件 (2)(共25张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 337.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览


文档简介
21.2 用函数观点看一元 二次方程(复习课)
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
驶向胜利的彼岸
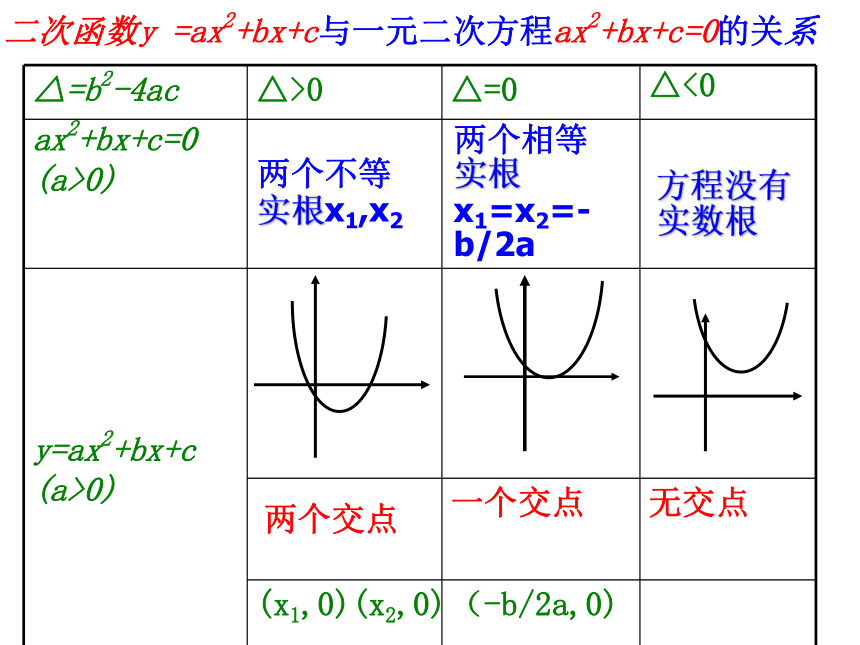
思考:二次函数与一元二次方程有什么联系?
知识回顾:
(-b/2a,0)
(x1,0)(x2,0)
无交点
一个交点
y=ax2+bx+c
(a>0)
ax2+bx+c=0
(a>0)
△<0
△=0
△>0
△=b2-4ac
方程没有实数根
两个不等实根x1,x2
两个相等实根x1=x2=-b/2a
二次函数y =ax2+bx+c与一元二次方程ax2+bx+c=0的关系
两个交点
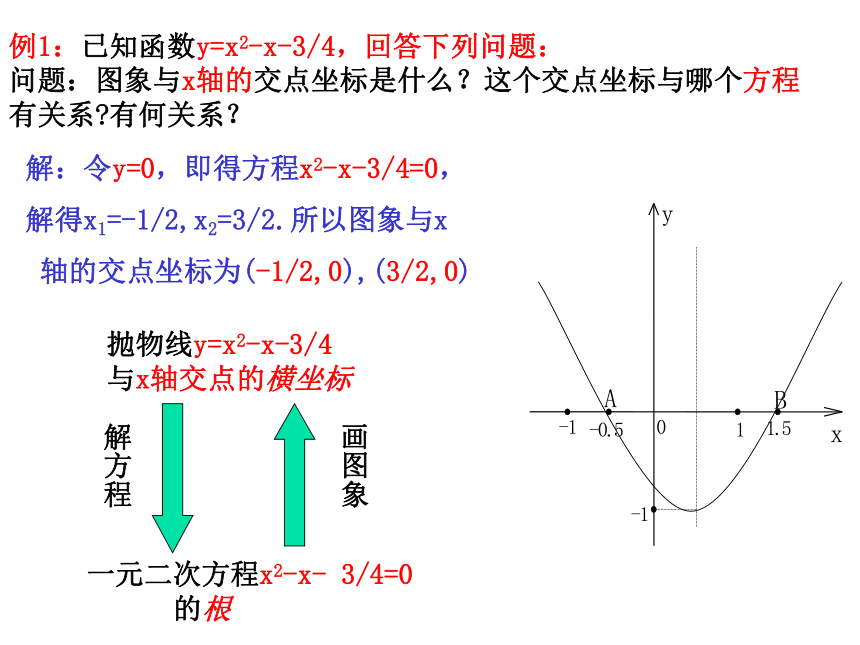
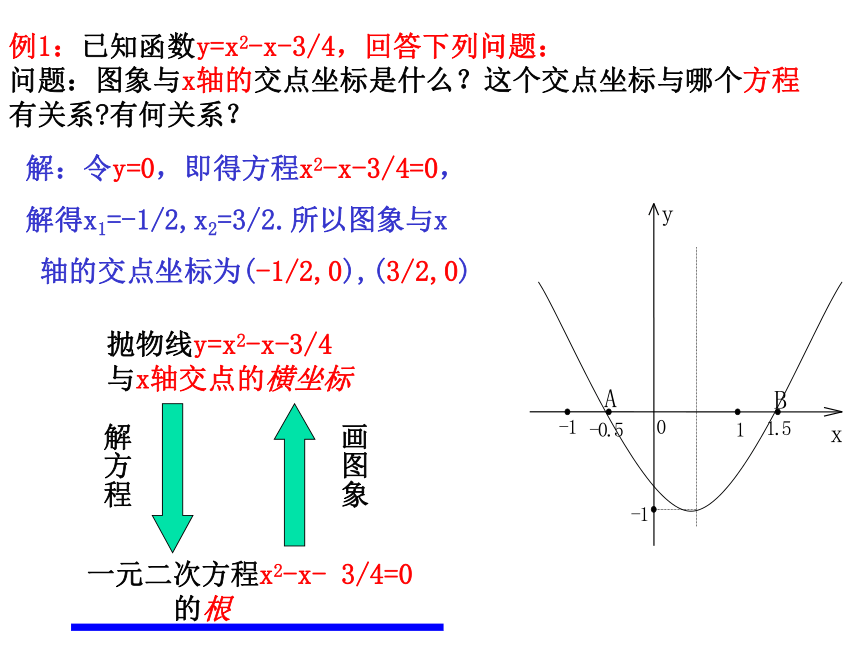
例1:已知函数y=x2-x-3/4,回答下列问题:
问题:图象与x轴的交点坐标是什么?这个交点坐标与哪个方程 有关系?有何关系?
解:令y=0,即得方程x2-x-3/4=0,
解得x1=-1/2,x2=3/2.所以图象与x
轴的交点坐标为(-1/2,0),(3/2,0)
一元二次方程x2-x- 3/4=0
的根
抛物线y=x2-x-3/4
与x轴交点的横坐标
1
.
5
y
x
-
0
.
5
-
1
-
1
1
B
A
0
解方程
画图象
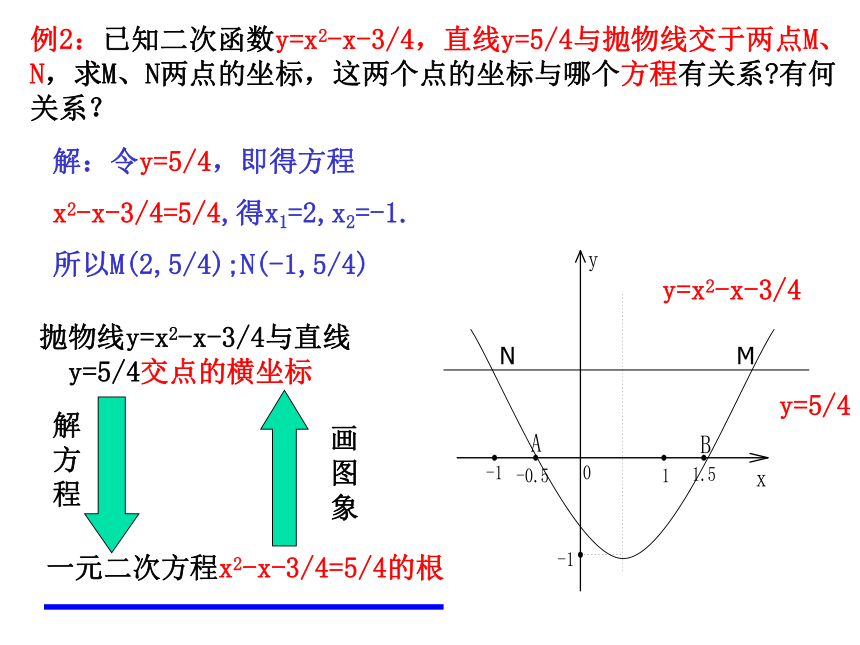
解:令y=5/4,即得方程
x2-x-3/4=5/4,得x1=2,x2=-1.
所以M(2,5/4);N(-1,5/4)
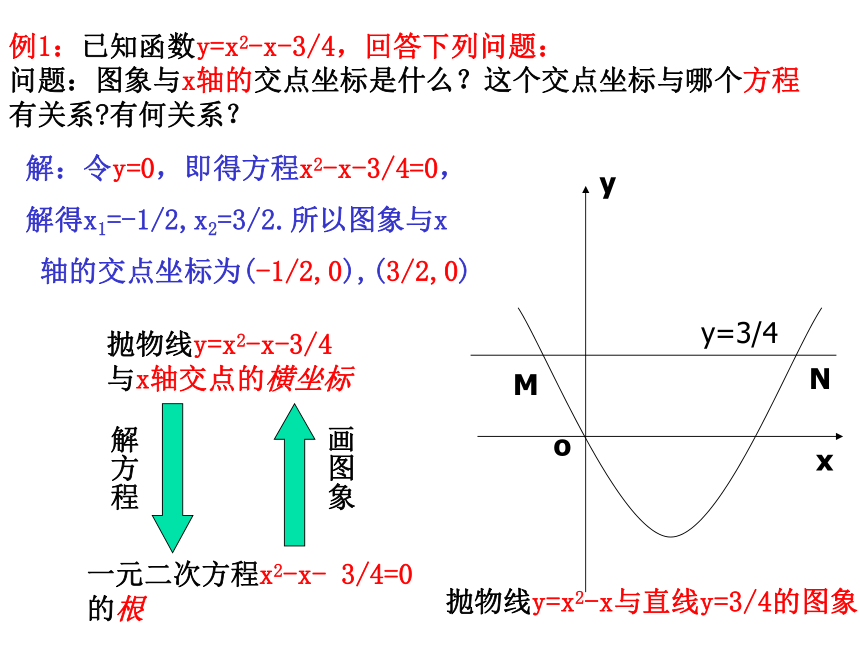
例2:已知二次函数y=x2-x-3/4,直线y=5/4与抛物线交于两点M、N,求M、N两点的坐标,这两个点的坐标与哪个方程有关系?有何关系?
N
M
抛物线y=x2-x-3/4与直线
y=5/4交点的横坐标
一元二次方程x2-x-3/4=5/4的根
y=x2-x-3/4
y=5/4
解方程
画图象
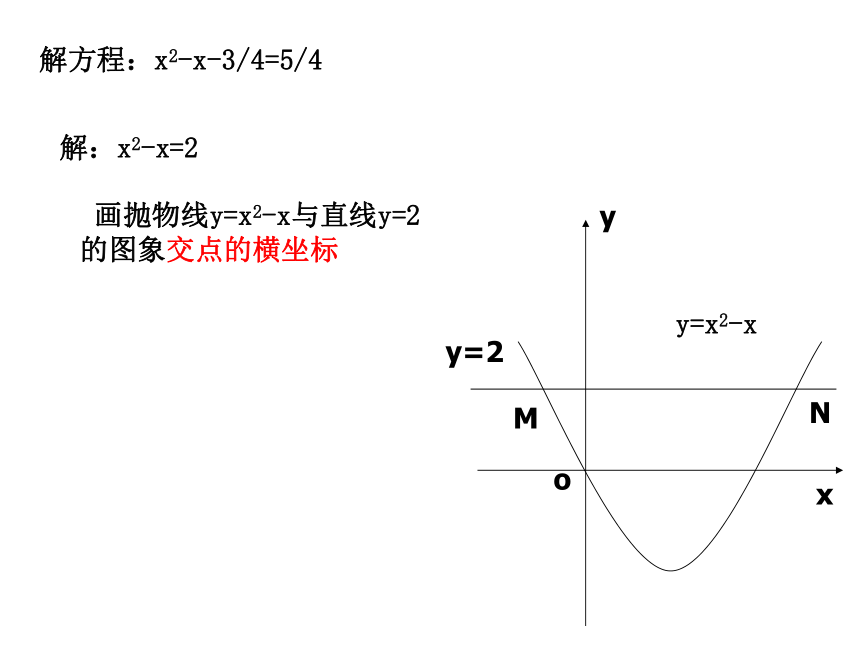
画抛物线y=x2-x与直线y=2 的图象交点的横坐标
解方程:x2-x-3/4=5/4
解:x2-x=2
o
y=x2-x
y=2
y
x
M
N
例1:已知函数y=x2-x-3/4,回答下列问题:
问题:图象与x轴的交点坐标是什么?这个交点坐标与哪个方程 有关系?有何关系?
解:令y=0,即得方程x2-x-3/4=0,
解得x1=-1/2,x2=3/2.所以图象与x
轴的交点坐标为(-1/2,0),(3/2,0)
一元二次方程x2-x- 3/4=0
的根
抛物线y=x2-x-3/4
与x轴交点的横坐标
1
.
5
y
x
-
0
.
5
-
1
-
1
1
B
A
0
解方程
画图象
例1:已知函数y=x2-x-3/4,回答下列问题:
问题:图象与x轴的交点坐标是什么?这个交点坐标与哪个方程 有关系?有何关系?
解:令y=0,即得方程x2-x-3/4=0,
解得x1=-1/2,x2=3/2.所以图象与x
轴的交点坐标为(-1/2,0),(3/2,0)
一元二次方程x2-x- 3/4=0
的根
抛物线y=x2-x-3/4
与x轴交点的横坐标
解方程
画图象
抛物线y=x2-x与直线y=3/4的图象
y
x
o
M
N
y=3/4
巩固与练习:
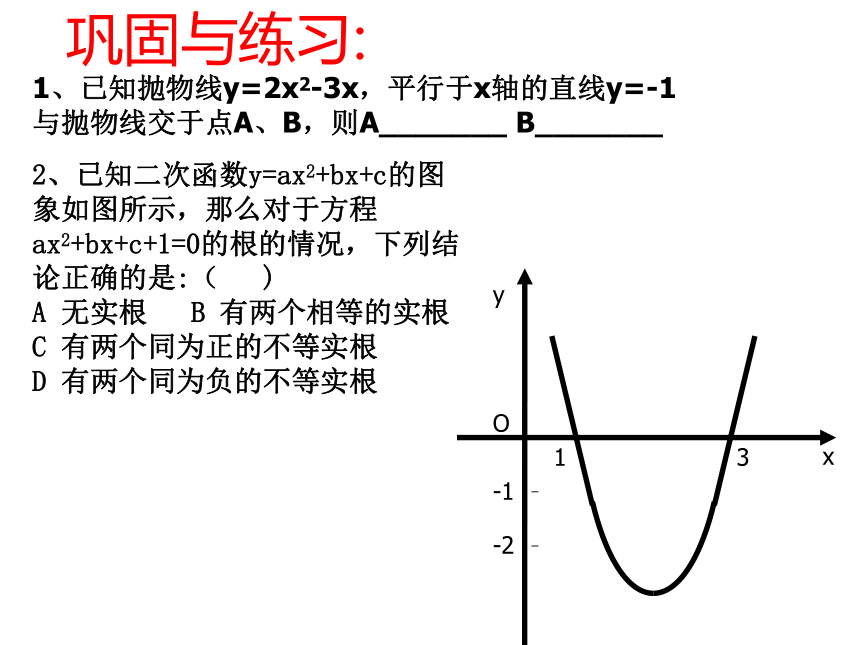
2、已知二次函数y=ax2+bx+c的图象如图所示,那么对于方程ax2+bx+c+1=0的根的情况,下列结论正确的是:( )
A 无实根 B 有两个相等的实根
C 有两个同为正的不等实根
D 有两个同为负的不等实根
x
y
1
3
O
-1
-2
1、已知抛物线y=2x2-3x,平行于x轴的直线y=-1
与抛物线交于点A、B,则A_______ B_______
巩固与练习:
2、已知二次函数y=ax2+bx+c的图象如图所示,那么对于方程
ax2+bx+c+1=0的根的情况,下列结论正确的是:( )
A 无实根 B 有两个相等的实根
C 有两个同为正的不等实根
D 有两个同为负的不等实根
x
y
1
3
O
-1
-2
1、已知抛物线y=2x2-3x,平行于x轴的直线y=-1
与抛物线线交于点A、B,则A(1,-1) B(1/2,-1)
巩固与练习:
2、已知二次函数y=ax2+bx+c的图象如图所示,那么对于方程ax2+bx+c+1=0的根的情况,下列结论正确的是:( C )
A 无实根 B 有两个相等的实根
C 有两个同为正的不等实根
D 有两个同为负的不等实根
x
y
1
3
O
-1
-2
1、已知抛物线y=2x2-3x,平行于x轴的直线y=-1
与抛物线线交于点A、B,则A(1,-1) B(1/2,-1)
巩固与练习:
3、已知方程x2 - 3x/2 = k
(1)若方程有实数根,求实数k的取值围。
巩固与练习:
3、已知方程x2 - 3x/2 = k
(1)若方程有实数根,求实数k的取值围。
解:依题意,X2 - 3x/2 -k=0,整理得
2x2-3x-2k=0,△≥0,
则9+16k ≥0,解得k ≥ - 9/16
巩固与练习:
3、已知方程x2 - 3x/2 = k
(1)若方程有实数根,求实数k的取值围。
解:如图,抛物线
y=x2-3x/2与直线y=k的交点
的横坐标即为方程x2-3x/2=k
的根,因为抛物线最低点
纵坐标为-9/16,所以k ≥
-9/16
-9/16
O
x
y
巩固与练习:
y
O
x
3、已知方程x2 - 3x/2 = k
(2)若方程当0≤x≤1时有两个不等实数根,求实数k的
取值范围。
3/2
x=3/4
1
巩固与练习:
解:如图:抛物线y=x2 - 3x/2
与直线y=k的交点的横坐标即
为方程x2 - 3x/2 = k的根,∵抛
物线最低点的纵坐标为-9/16,
当x=-1时,可求它对应的y=-1/2,
而当x=0时y=0, ∴k的取值范围为
-9/16<k≤-1/2
-9/16
y
O
x
3、已知方程x2 - 3x/2 = k
(2)若方程当0≤x≤1时有两个不等实数根,求实数k的
取值范围。
3/2
x=3/4
1
-1/2
例3:已知二次函数y1=x2 – x - 3/4,直线y2=x + 9/4与抛物线交于两点M、N,求M、N两点的坐标,这两个点的坐标与哪个方程有关系?有何关系?
y
O
x
M
N
则M(-1,5/4),N(3,21/4)
方程x2-x-3/4=5/4的根
x2 -x-3/4 = x + 9/4
解: 令 y1=y2
解得x1=3,x2=-1
y1=21/4 y2=5/4
y
O
x
方程x2-x-3/4=5/4的根
解方程:x2 -x-3/4 = x + 9/4
解:移项得 x2 -2x=3
画抛物线y=x2 -2x和直线
y=3的图象
M
N
巩固与练习:
4、已知抛物线y=x2 - 5x - 6 ,若直线y=x+m与此抛
物线只有一个公共点P,求P点的坐标。
巩固与练习:
4、已知抛物线y=x2 - 5x - 6 ,若直线y=x+m与此抛
物线只有一个公共点P,求P点的坐标。
解:依题意x2 - 5x – 6=x+m
整理得 x2 - 6x – 6 - m=0
依题意可知 △=0
36+4(6+m)=0
解得 m=-15
(1 )
把m=-15代入(1)式得 x2 - 6x + 9 = 0
解得 x=3
把x=3 代入y=x2 - 5x - 6 ,得y=-12 ∴点P(3,-12)
巩固与练习:
4、已知抛物线y=x2 - 5x - 6,若直线y=x+m与此抛
物线只有一个公共点P,求P点的坐标。
解:依题意得x2 - 5x - 6 =x+m
移项得x2 - 6x =m+6
画抛物线y=x2 - 6x和直线
y=m+6的图象
y
O
x
巩固与练习:
4、已知抛物线y=x2 - 5x - 6,若直线y=x+m与此抛
物线只有一个公共点P,求P点的坐标。
解:依题意得x2 - 5x - 6 =x+m
移项得x2 - 6x =m+6
画抛物线y=x2 - 6x和直线
y=m+6的图象
y
O
x
顶 点
抛物线y=x2 - 6x的顶点
坐标为(3,-12)
∴点P(3,-12)
P
X
y=ax2+bx+c
求抛物线与直线 的交点
y
o
解一元二次方程
归纳小结
y=mx+n
y=n
ax2+bx+c=0
ax2+bx+c=n
ax2+bx+c=mx+n
知识提升:
求函数图象
的交点坐标
解方程
解方程
画函数的图象
数形结合思想
课后思考:
已知抛物线y=-x2+bx+c的顶点P在双曲线y=k/x上,
对称轴是直线x=1,且抛物线经过点A(3,2)
(1)求抛物线和双曲线的解析式
(2)设抛物线和双曲线另外两个交点为B、C
(B点在第一象限),求经过B,C两点的直线的解析式
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
驶向胜利的彼岸
思考:二次函数与一元二次方程有什么联系?
知识回顾:
(-b/2a,0)
(x1,0)(x2,0)
无交点
一个交点
y=ax2+bx+c
(a>0)
ax2+bx+c=0
(a>0)
△<0
△=0
△>0
△=b2-4ac
方程没有实数根
两个不等实根x1,x2
两个相等实根x1=x2=-b/2a
二次函数y =ax2+bx+c与一元二次方程ax2+bx+c=0的关系
两个交点
例1:已知函数y=x2-x-3/4,回答下列问题:
问题:图象与x轴的交点坐标是什么?这个交点坐标与哪个方程 有关系?有何关系?
解:令y=0,即得方程x2-x-3/4=0,
解得x1=-1/2,x2=3/2.所以图象与x
轴的交点坐标为(-1/2,0),(3/2,0)
一元二次方程x2-x- 3/4=0
的根
抛物线y=x2-x-3/4
与x轴交点的横坐标
1
.
5
y
x
-
0
.
5
-
1
-
1
1
B
A
0
解方程
画图象
解:令y=5/4,即得方程
x2-x-3/4=5/4,得x1=2,x2=-1.
所以M(2,5/4);N(-1,5/4)
例2:已知二次函数y=x2-x-3/4,直线y=5/4与抛物线交于两点M、N,求M、N两点的坐标,这两个点的坐标与哪个方程有关系?有何关系?
N
M
抛物线y=x2-x-3/4与直线
y=5/4交点的横坐标
一元二次方程x2-x-3/4=5/4的根
y=x2-x-3/4
y=5/4
解方程
画图象
画抛物线y=x2-x与直线y=2 的图象交点的横坐标
解方程:x2-x-3/4=5/4
解:x2-x=2
o
y=x2-x
y=2
y
x
M
N
例1:已知函数y=x2-x-3/4,回答下列问题:
问题:图象与x轴的交点坐标是什么?这个交点坐标与哪个方程 有关系?有何关系?
解:令y=0,即得方程x2-x-3/4=0,
解得x1=-1/2,x2=3/2.所以图象与x
轴的交点坐标为(-1/2,0),(3/2,0)
一元二次方程x2-x- 3/4=0
的根
抛物线y=x2-x-3/4
与x轴交点的横坐标
1
.
5
y
x
-
0
.
5
-
1
-
1
1
B
A
0
解方程
画图象
例1:已知函数y=x2-x-3/4,回答下列问题:
问题:图象与x轴的交点坐标是什么?这个交点坐标与哪个方程 有关系?有何关系?
解:令y=0,即得方程x2-x-3/4=0,
解得x1=-1/2,x2=3/2.所以图象与x
轴的交点坐标为(-1/2,0),(3/2,0)
一元二次方程x2-x- 3/4=0
的根
抛物线y=x2-x-3/4
与x轴交点的横坐标
解方程
画图象
抛物线y=x2-x与直线y=3/4的图象
y
x
o
M
N
y=3/4
巩固与练习:
2、已知二次函数y=ax2+bx+c的图象如图所示,那么对于方程ax2+bx+c+1=0的根的情况,下列结论正确的是:( )
A 无实根 B 有两个相等的实根
C 有两个同为正的不等实根
D 有两个同为负的不等实根
x
y
1
3
O
-1
-2
1、已知抛物线y=2x2-3x,平行于x轴的直线y=-1
与抛物线交于点A、B,则A_______ B_______
巩固与练习:
2、已知二次函数y=ax2+bx+c的图象如图所示,那么对于方程
ax2+bx+c+1=0的根的情况,下列结论正确的是:( )
A 无实根 B 有两个相等的实根
C 有两个同为正的不等实根
D 有两个同为负的不等实根
x
y
1
3
O
-1
-2
1、已知抛物线y=2x2-3x,平行于x轴的直线y=-1
与抛物线线交于点A、B,则A(1,-1) B(1/2,-1)
巩固与练习:
2、已知二次函数y=ax2+bx+c的图象如图所示,那么对于方程ax2+bx+c+1=0的根的情况,下列结论正确的是:( C )
A 无实根 B 有两个相等的实根
C 有两个同为正的不等实根
D 有两个同为负的不等实根
x
y
1
3
O
-1
-2
1、已知抛物线y=2x2-3x,平行于x轴的直线y=-1
与抛物线线交于点A、B,则A(1,-1) B(1/2,-1)
巩固与练习:
3、已知方程x2 - 3x/2 = k
(1)若方程有实数根,求实数k的取值围。
巩固与练习:
3、已知方程x2 - 3x/2 = k
(1)若方程有实数根,求实数k的取值围。
解:依题意,X2 - 3x/2 -k=0,整理得
2x2-3x-2k=0,△≥0,
则9+16k ≥0,解得k ≥ - 9/16
巩固与练习:
3、已知方程x2 - 3x/2 = k
(1)若方程有实数根,求实数k的取值围。
解:如图,抛物线
y=x2-3x/2与直线y=k的交点
的横坐标即为方程x2-3x/2=k
的根,因为抛物线最低点
纵坐标为-9/16,所以k ≥
-9/16
-9/16
O
x
y
巩固与练习:
y
O
x
3、已知方程x2 - 3x/2 = k
(2)若方程当0≤x≤1时有两个不等实数根,求实数k的
取值范围。
3/2
x=3/4
1
巩固与练习:
解:如图:抛物线y=x2 - 3x/2
与直线y=k的交点的横坐标即
为方程x2 - 3x/2 = k的根,∵抛
物线最低点的纵坐标为-9/16,
当x=-1时,可求它对应的y=-1/2,
而当x=0时y=0, ∴k的取值范围为
-9/16<k≤-1/2
-9/16
y
O
x
3、已知方程x2 - 3x/2 = k
(2)若方程当0≤x≤1时有两个不等实数根,求实数k的
取值范围。
3/2
x=3/4
1
-1/2
例3:已知二次函数y1=x2 – x - 3/4,直线y2=x + 9/4与抛物线交于两点M、N,求M、N两点的坐标,这两个点的坐标与哪个方程有关系?有何关系?
y
O
x
M
N
则M(-1,5/4),N(3,21/4)
方程x2-x-3/4=5/4的根
x2 -x-3/4 = x + 9/4
解: 令 y1=y2
解得x1=3,x2=-1
y1=21/4 y2=5/4
y
O
x
方程x2-x-3/4=5/4的根
解方程:x2 -x-3/4 = x + 9/4
解:移项得 x2 -2x=3
画抛物线y=x2 -2x和直线
y=3的图象
M
N
巩固与练习:
4、已知抛物线y=x2 - 5x - 6 ,若直线y=x+m与此抛
物线只有一个公共点P,求P点的坐标。
巩固与练习:
4、已知抛物线y=x2 - 5x - 6 ,若直线y=x+m与此抛
物线只有一个公共点P,求P点的坐标。
解:依题意x2 - 5x – 6=x+m
整理得 x2 - 6x – 6 - m=0
依题意可知 △=0
36+4(6+m)=0
解得 m=-15
(1 )
把m=-15代入(1)式得 x2 - 6x + 9 = 0
解得 x=3
把x=3 代入y=x2 - 5x - 6 ,得y=-12 ∴点P(3,-12)
巩固与练习:
4、已知抛物线y=x2 - 5x - 6,若直线y=x+m与此抛
物线只有一个公共点P,求P点的坐标。
解:依题意得x2 - 5x - 6 =x+m
移项得x2 - 6x =m+6
画抛物线y=x2 - 6x和直线
y=m+6的图象
y
O
x
巩固与练习:
4、已知抛物线y=x2 - 5x - 6,若直线y=x+m与此抛
物线只有一个公共点P,求P点的坐标。
解:依题意得x2 - 5x - 6 =x+m
移项得x2 - 6x =m+6
画抛物线y=x2 - 6x和直线
y=m+6的图象
y
O
x
顶 点
抛物线y=x2 - 6x的顶点
坐标为(3,-12)
∴点P(3,-12)
P
X
y=ax2+bx+c
求抛物线与直线 的交点
y
o
解一元二次方程
归纳小结
y=mx+n
y=n
ax2+bx+c=0
ax2+bx+c=n
ax2+bx+c=mx+n
知识提升:
求函数图象
的交点坐标
解方程
解方程
画函数的图象
数形结合思想
课后思考:
已知抛物线y=-x2+bx+c的顶点P在双曲线y=k/x上,
对称轴是直线x=1,且抛物线经过点A(3,2)
(1)求抛物线和双曲线的解析式
(2)设抛物线和双曲线另外两个交点为B、C
(B点在第一象限),求经过B,C两点的直线的解析式
同课章节目录
