2020-2021学年人教版数学九年级上册二次函数与一元二次方程(共20张ppt)
文档属性
| 名称 | 2020-2021学年人教版数学九年级上册二次函数与一元二次方程(共20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 19:40:26 | ||
图片预览







文档简介
二次函数与一元二次方程
一、探究
探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标.
解:∵A、B在x轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0)
,
B(2,0)
你发现方程
的解x1、x2与A、B的坐标有什么联系?
x2-3x+2=0
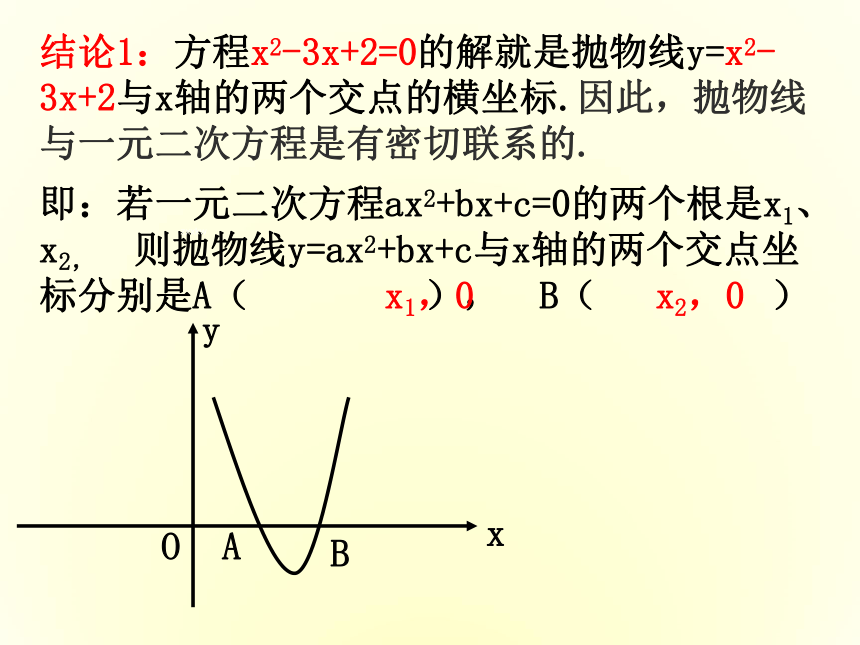
结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标.因此,抛物线与一元二次方程是有密切联系的.
即:若一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(
),
B(
)
x1,0
x2,0
x
O
A
B
y
w
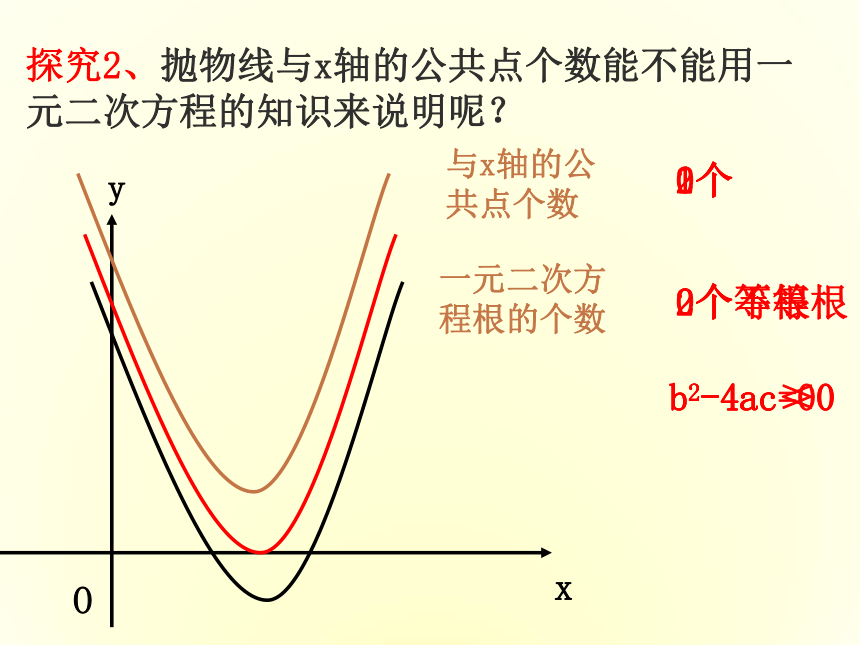
探究2、抛物线与x轴的公共点个数能不能用一元二次方程的知识来说明呢?
O
x
y
与x轴的公共点个数
一元二次方程根的个数
2个
2个不等根
b2-4ac>0
1个
2个等根
0个
0个
b2-4ac<0
b2-4ac=0
一元二次方程ax2+bx+c=0有两个不等的实数根
结论2:
抛物线y=ax2+bx+c与x轴有两个公共点
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
抛物线y=ax2+bx+c与x轴有唯一公共点
一元二次方程ax2+bx+c=0有两个相等的实数根
抛物线y=ax2+bx+c与x轴没有公共点
一元二次方程ax2+bx+c=0没有实数根
1、b2-4ac>0
2、
b2-4ac
=0
3、
b2-4ac
<0
1、下列各抛物线与x轴是否有公共点,如果有,求出公共点的坐标.
(1)y=6x2-2x+1
(2)y=-15x2+14x+8
(3)y=x2-4x+4
关键:令y=0时,看b2-4ac.
二、基础训练
2、判断下列各抛物线与坐标轴的交点个数.
(1)y=6x2-2x+1
(2)y=2x2-6x
基础训练
3、已知抛物线y=x2-6x+a的顶点在x轴上,则a=
;若抛物线与x轴有两个交点,则a的范围是
;若抛物线与坐标轴有两个公共点,则a=
;
顶点在x轴上
b2-4ac=0
与x轴有两个交点
方程有两个不等实根
x
y
o
9
a<9
9或0
基础训练
4、已知抛物线y=x2-3x+a+1与x轴最多只有
一个公共点,则a的范围是
.
5、关于x的方程x2-x-n=0没有实数根,则抛物
线y=x2-x-n的顶点在
象限.
第一
基础训练
w
1、已知抛物线y=x2+2x+m+1与x轴只有一个公共点,求m的值.
三、例题分析:
2、求证:不论k取何值时,抛物线y=x2-kx-2+k与x轴总有两个不同的交点.
例题分析:
同学们:再见!
知识就象一艘船
让它载着你
驶向你理想的彼岸
3、抛物线y=-x2-x+12如图所示
o
y
x
A(-4,0)
B(3,0)
y=-x2-x+12
x
时,y>0.
x
时,
y<0.
-4x<-4或x>3
x
时,y=0.
=-4或3
例题分析:
4、(1)抛物线y=ax2+bx+c在x轴上方的条件是什么?
(2)抛物线y=ax2+bx+c
在x轴下方的条件是什么?
x
x
例题分析:
(3)不论x取何值时,函数y=ax2+bx+c(a≠0)的值永远是正值的条件是什么?
(4)已知:抛物线y=mx2-2(3m-1)x+9m-1,无
论x取何值时,函数y的值都是非负数.
求:m的取值范围.
x
例题分析:
w
5、
已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.
x
y
o
A
B
D
C
-1
5
-2.5
y=
(x+1)(x-5)
=
(x-2)2-
例题分析:
x
y
o
A
B
D
C
-1
5
-2.5
5、
已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.
例题分析:
y=
(x+1)(x-5)
=
(x-2)2-
x
y
o
A
B
D
C
-1
5
-2.5
5、
已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.
例题分析:
y=
(x+1)(x-5)
=
(x-2)2-
x
y
o
A
B
D
C
-1
5
-2.5
5、
已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.
例题分析:
y=
(x+1)(x-5)
=
(x-2)2-
w
四、小结
1、若一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0
),
B(
x2,0
)
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系.体现了数形结合的思想.
w
w
一、探究
探究1、求二次函数图象y=x2-3x+2与x轴的交点A、B的坐标.
解:∵A、B在x轴上,
∴它们的纵坐标为0,
∴令y=0,则x2-3x+2=0
解得:x1=1,x2=2;
∴A(1,0)
,
B(2,0)
你发现方程
的解x1、x2与A、B的坐标有什么联系?
x2-3x+2=0
结论1:方程x2-3x+2=0的解就是抛物线y=x2-3x+2与x轴的两个交点的横坐标.因此,抛物线与一元二次方程是有密切联系的.
即:若一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(
),
B(
)
x1,0
x2,0
x
O
A
B
y
w
探究2、抛物线与x轴的公共点个数能不能用一元二次方程的知识来说明呢?
O
x
y
与x轴的公共点个数
一元二次方程根的个数
2个
2个不等根
b2-4ac>0
1个
2个等根
0个
0个
b2-4ac<0
b2-4ac=0
一元二次方程ax2+bx+c=0有两个不等的实数根
结论2:
抛物线y=ax2+bx+c与x轴有两个公共点
抛物线y=ax2+bx+c与x轴的交点个数可由
一元二次方程ax2+bx+c=0的根的情况说明:
抛物线y=ax2+bx+c与x轴有唯一公共点
一元二次方程ax2+bx+c=0有两个相等的实数根
抛物线y=ax2+bx+c与x轴没有公共点
一元二次方程ax2+bx+c=0没有实数根
1、b2-4ac>0
2、
b2-4ac
=0
3、
b2-4ac
<0
1、下列各抛物线与x轴是否有公共点,如果有,求出公共点的坐标.
(1)y=6x2-2x+1
(2)y=-15x2+14x+8
(3)y=x2-4x+4
关键:令y=0时,看b2-4ac.
二、基础训练
2、判断下列各抛物线与坐标轴的交点个数.
(1)y=6x2-2x+1
(2)y=2x2-6x
基础训练
3、已知抛物线y=x2-6x+a的顶点在x轴上,则a=
;若抛物线与x轴有两个交点,则a的范围是
;若抛物线与坐标轴有两个公共点,则a=
;
顶点在x轴上
b2-4ac=0
与x轴有两个交点
方程有两个不等实根
x
y
o
9
a<9
9或0
基础训练
4、已知抛物线y=x2-3x+a+1与x轴最多只有
一个公共点,则a的范围是
.
5、关于x的方程x2-x-n=0没有实数根,则抛物
线y=x2-x-n的顶点在
象限.
第一
基础训练
w
1、已知抛物线y=x2+2x+m+1与x轴只有一个公共点,求m的值.
三、例题分析:
2、求证:不论k取何值时,抛物线y=x2-kx-2+k与x轴总有两个不同的交点.
例题分析:
同学们:再见!
知识就象一艘船
让它载着你
驶向你理想的彼岸
3、抛物线y=-x2-x+12如图所示
o
y
x
A(-4,0)
B(3,0)
y=-x2-x+12
x
时,y>0.
x
时,
y<0.
-4
x
时,y=0.
=-4或3
例题分析:
4、(1)抛物线y=ax2+bx+c在x轴上方的条件是什么?
(2)抛物线y=ax2+bx+c
在x轴下方的条件是什么?
x
x
例题分析:
(3)不论x取何值时,函数y=ax2+bx+c(a≠0)的值永远是正值的条件是什么?
(4)已知:抛物线y=mx2-2(3m-1)x+9m-1,无
论x取何值时,函数y的值都是非负数.
求:m的取值范围.
x
例题分析:
w
5、
已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.
x
y
o
A
B
D
C
-1
5
-2.5
y=
(x+1)(x-5)
=
(x-2)2-
例题分析:
x
y
o
A
B
D
C
-1
5
-2.5
5、
已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.
例题分析:
y=
(x+1)(x-5)
=
(x-2)2-
x
y
o
A
B
D
C
-1
5
-2.5
5、
已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.
例题分析:
y=
(x+1)(x-5)
=
(x-2)2-
x
y
o
A
B
D
C
-1
5
-2.5
5、
已知:抛物线y=ax2+bx+c的图象如图所示:
(1)求此抛物线的解析式;
(2)当x取何值时,y>0?
(3)将抛物线作怎样的一次
平移,才能使它与坐标轴仅有
两个交点,并写出此时抛物线
的解析式.
例题分析:
y=
(x+1)(x-5)
=
(x-2)2-
w
四、小结
1、若一元二次方程ax2+bx+c=0的两个根是x1、x2,
则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A(x1,0
),
B(
x2,0
)
2、若一元二次方程ax2+bx+c=0与二次三项式ax2+bx+c及二次函数y=ax2+bx+c这三个“二次”之间互相转化的关系.体现了数形结合的思想.
w
w
同课章节目录
