吉林省长春市名校2020-2021学年高二下学期期末考试数学(理)试题 Word版含答案
文档属性
| 名称 | 吉林省长春市名校2020-2021学年高二下学期期末考试数学(理)试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 711.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览


文档简介
长春市名校2020-2021学年高二下学期期末考试
理科数学试卷
考试时间:120分钟 分值:150分
选择题(本大题共12小题,共60分)
1.若复数的共辄复数为且满足,则复数的虚部为( )
A. B. C. D.
2. 展开式中,的系数为( )
A.126 B.-84 C.84 D.-126
3.下列说法中正确的是( )
A.若一组数据1,,3的平均数是2,则该组数据的方差是
B.线性回归直线不一定过样本中心点
C.若两个随机变量的线性相关越强,则相关系数的值越接近于1
D.先把高三年级的2000名学生编号:1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为,然后抽取编号为+50,+100,+150,……的学生,这样的抽样方法是分层抽样
4.甲、乙、丙三个同学在看,,三位运动员进行“乒乓球冠军争夺赛”赛前,对于谁会得冠军进行预测,甲说:不是,是;乙说:不是,是;丙说:不是,是.比赛结果表明,他们的话有一人全对,有一人对一半错一半,有一人全错,则冠军是( )
A. B. C. D.不能预测
5.若曲线在点处的切线与直线平行,则实数的值为( )
A. B. C.1 D.2
6. 用数学归纳法证明:1+++时,在第二步证明从n=k到n=k+1成立时,左边增加的项数是
A. B. C. D.
7.某班有60名学生,一次考试后数学成绩,若,则估计该班学生数学成绩在120分以上的人数为
A.10 B.9 C.8 D.7
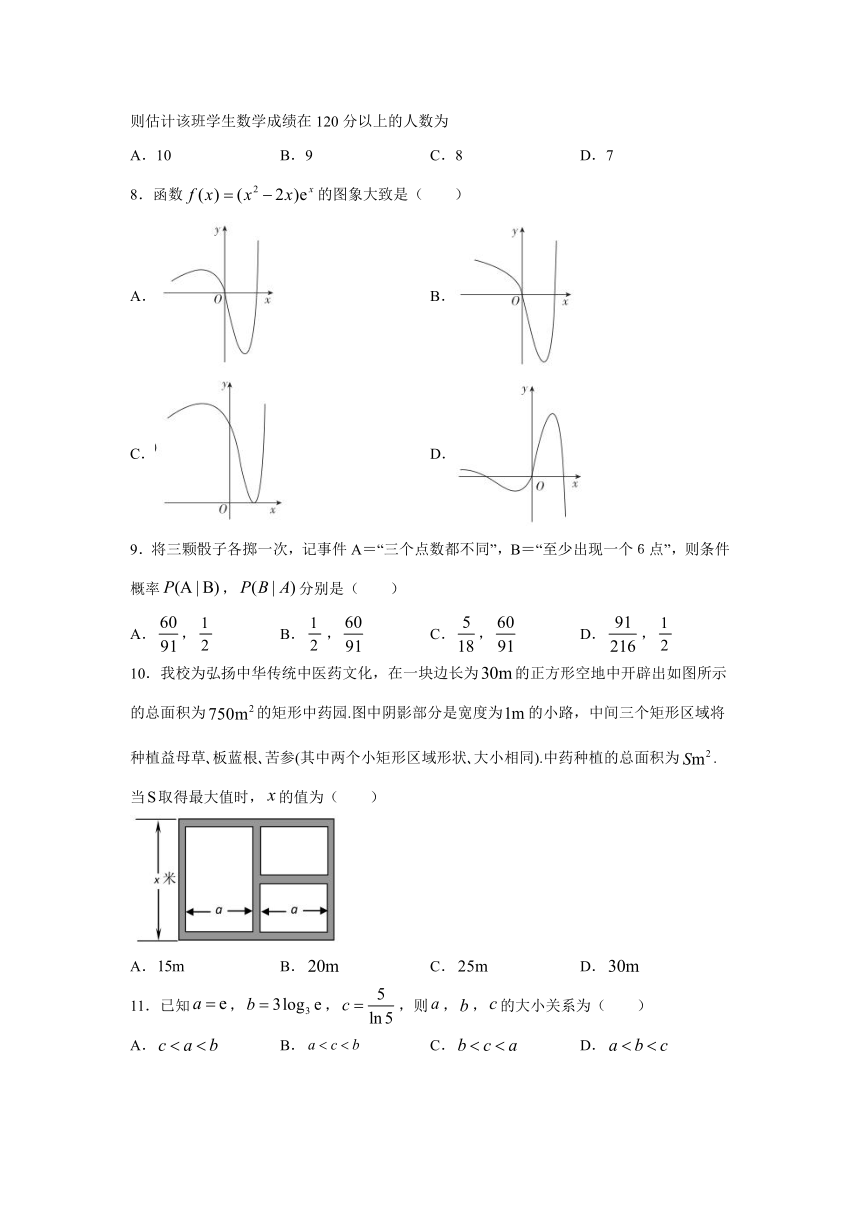
8.函数的图象大致是( )
A. B.
C. D.
9.将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率,分别是( )
A., B., C., D.,
10.我校为弘扬中华传统中医药文化,在一块边长为的正方形空地中开辟出如图所示的总面积为的矩形中药园.图中阴影部分是宽度为的小路,中间三个矩形区域将种植益母草?板蓝根?苦参(其中两个小矩形区域形状?大小相同).中药种植的总面积为.当取得最大值时,的值为( )
A. B. C. D.
11.已知,,,则,,的大小关系为( )
A. B. C. D.
12.已知,函数,若函数恰有三个零点,则( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
13.平面内一点到直线:的距离为:.由此类比,空间中一点到平面:的距离为______.
14.如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为_____.
15.为庆祝中国共产党成立100周年,某校以班级为单位组织开展“走进革命老区,学习党史文化”研学游活动.该校高一年级部10个班级分别去3个革命老区开展研学游,每个班级只去1个革命老区,每个革命老区至少安排3个班级,则不同的安排方法共有_____种(用数字作答).
16.已知函数与的图象上存在关于轴对称的点,则的取值范围为_____.
三、解答题(本大题共6小题,共70分)
17.(10分)已知函数.
(1)解不等式;
(2)若的定义域为,求实数的取值范围.
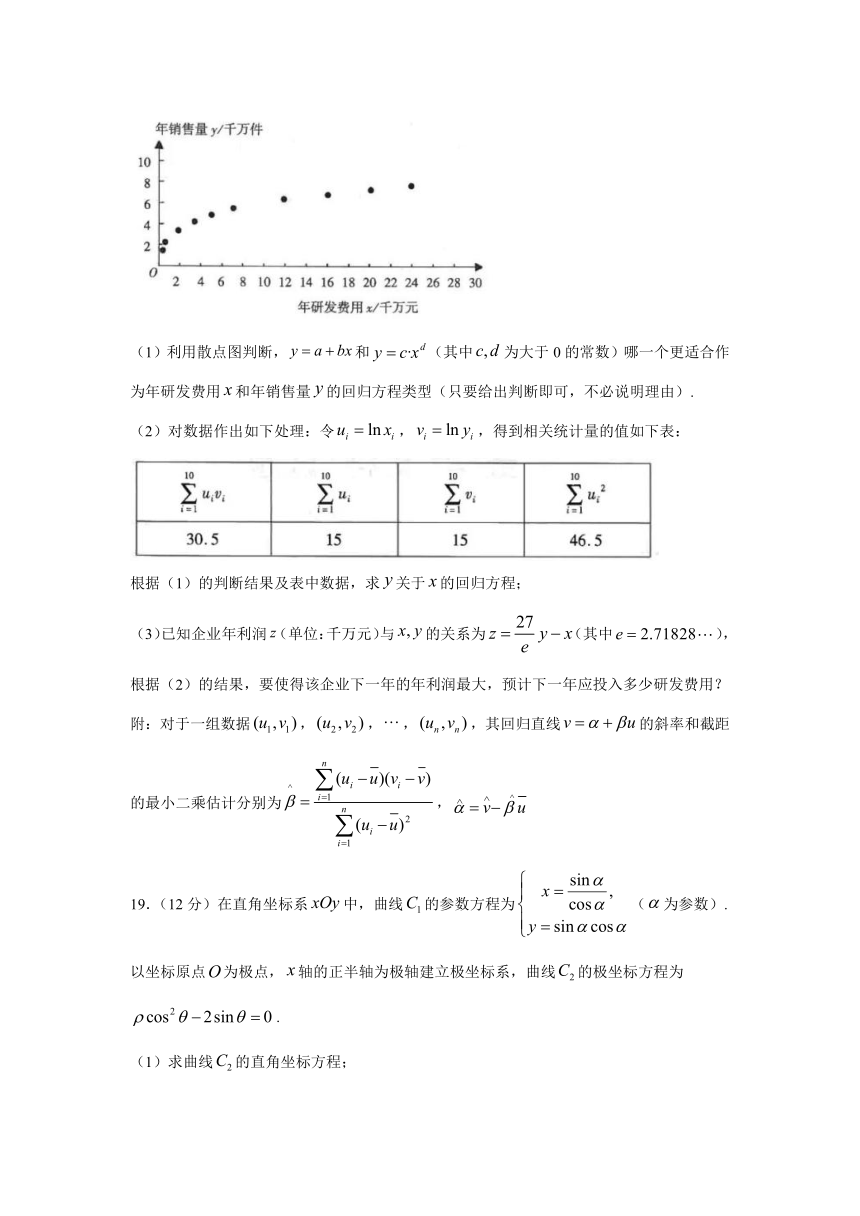
18.(12分)某企业为确定下一年投入某种产品的研发费用,需了解年研发费用(单位:千万元)对年销售量(单位:千万件)的影响,统计了近10年投入的年研发费用与年销售量的数据,得到散点图如图所示:
(1)利用散点图判断,和(其中为大于0的常数)哪一个更适合作为年研发费用和年销售量的回归方程类型(只要给出判断即可,不必说明理由).
(2)对数据作出如下处理:令,,得到相关统计量的值如下表:
根据(1)的判断结果及表中数据,求关于的回归方程;
(3)已知企业年利润(单位:千万元)与的关系为(其中),根据(2)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
附:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为,
19.(12分)在直角坐标系中,曲线的参数方程为(为参数).以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线的直角坐标方程;
(2)求曲线,公共点的直角坐标.
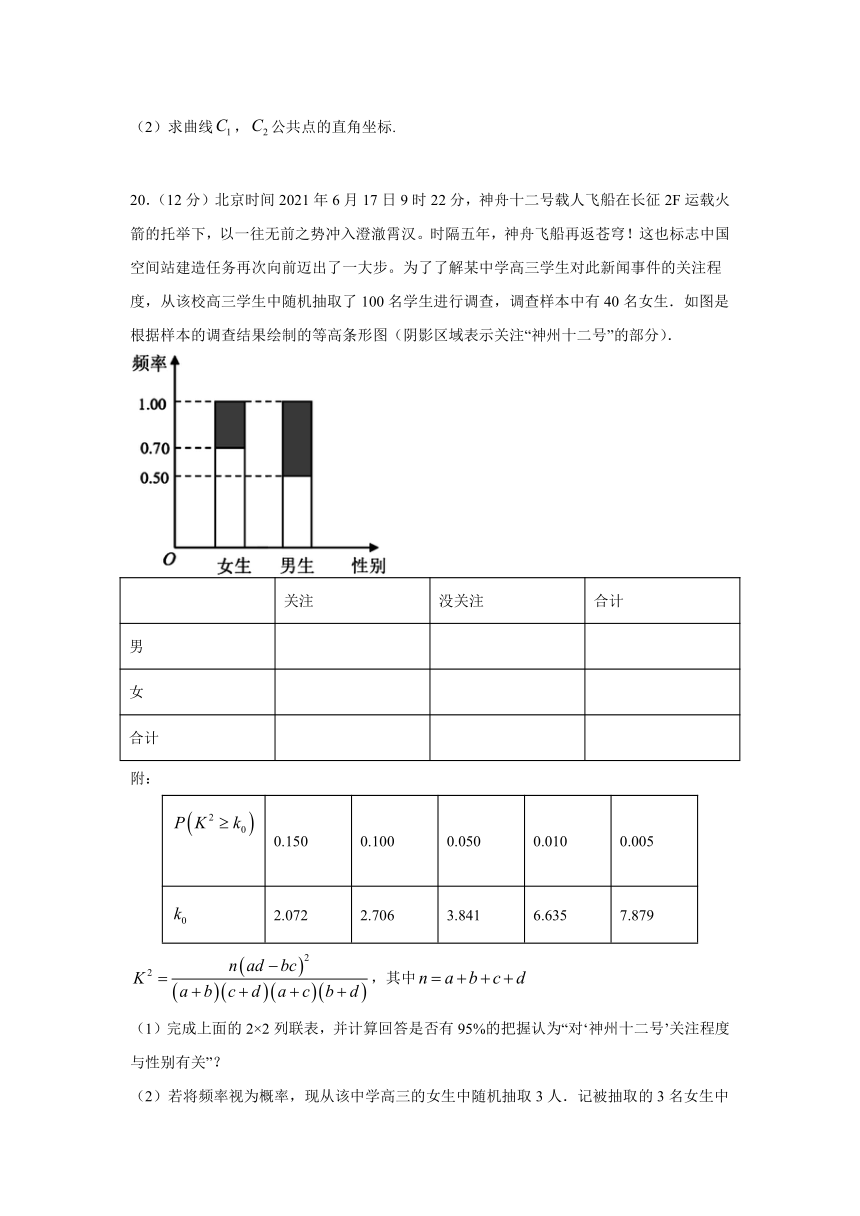
20.(12分)北京时间2021年6月17日9时22分,神舟十二号载人飞船在长征2F运载火箭的托举下,以一往无前之势冲入澄澈霄汉。时隔五年,神舟飞船再返苍穹!这也标志中国空间站建造任务再次向前迈出了一大步。为了了解某中学高三学生对此新闻事件的关注程度,从该校高三学生中随机抽取了100名学生进行调查,调查样本中有40名女生.如图是根据样本的调查结果绘制的等高条形图(阴影区域表示关注“神州十二号”的部分).
关注 没关注 合计
男
女
合计
附:
0.150 0.100 0.050 0.010 0.005
2.072 2.706 3.841 6.635 7.879
,其中
(1)完成上面的2×2列联表,并计算回答是否有95%的把握认为“对‘神州十二号’关注程度与性别有关”?
(2)若将频率视为概率,现从该中学高三的女生中随机抽取3人.记被抽取的3名女生中对“神州十二号”新闻关注的人数为随机变量,求的分布列及数学期望.
21.(12分)在平面直角坐标系中,直线的参数方程为:(为参数,),以为极点,轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为.
(1)当时,写出直线的普通方程和曲线的直角坐标方程;
(2)若点,设曲线与直线交于点,求的最小值.
22.(12分)已知函数(是自然对数的底数).
(1)求函数的单调区间;
(2)当,时,证明:.
长春市名校2020-2021学年高二下学期期末考试
理科数学答案
一、选择题
1.A 2.B 3.A 4.C 5.A 6.A
7. B 8.A 9.A 10.C 11.D 12.C
二、填空题
13. 14. 15.12600 16.
三、解答题
17.(Ⅰ)(Ⅱ)
(1)或或……………………………………………………3分
不等式的解集为 …………………………………………………………5分
(2)若的定义域为,则恒成立,即在上无解
又,的最小值为2, ……………9分
所以…………………………………………………………………………………10分
18.(1)选择回归类型;(2);(3)2.7亿元.
(1)由散点图知,选择回归类型更适合.………………………………1分
(2)对两边取对数,得,即…………………2分
由表中数据得:,
∴………4分
∴,
∴,…………………………………………………………………………………6分
∴年研发费用与年销售量的回归方程为.…………………………………7分
(3)由(2)知,,…………………………………8分
∴,
令,得,…………………………………10分
且当时,单调递增;当时,单调递减.
所以当千万元时,年利润取得最大值,且最大值为亿元.………………………………………………………………12分
答:要使年利润取最大值,预计下一年度投入2.7亿元.
19.(1);(2).
(1)由题意知,曲线的极坐标方程为,
即, ………………………………………2分
所以曲线的直角坐标方程为. ……………………………………4分
(2)曲线的参数方程为 …………………6分
所以曲线的直角坐标方程为. ………………………………………8分
由解得或
所以曲线公共点的直角坐标为.…………………………………12分
20.(1)填表见解析;有;(2)分布列见解析;期望为.
(1)列联表如下:………………………………………4分
关注 没关注 合计
男 30 30 60
女 12 28 40
合计 42 58 100
所以,
所以有95%的把握认为“对‘神州十二号’关注程度与性别有关”;…………………………6分
(2)因为随机选一个高三的女生,对此事关注的概率为,
又因为,所以随机变量的分布列为:………………………………8分
0 1 2 3
故.………………………………………12分
21.(1);;(2)
【详解】
(1)当时,直线的参数方程为:,
直线的普通方程为.………………………………2分
曲线的极坐标方程为,
,
曲线的直角坐标方程为,
即. …………………………………………………4分
(2)将直线的参数方程代入圆的直角坐标方程,
得,…………………………………………………6分
,
设是方程的两个根,
则,…………………………………………………8分
又直线过点,结合的几何意义得:
……………………………………10分
,
…………………………12分
22.(1)函数的单调增区间为,单调减区间为,;(2)证明见解析.
(1)由得,………………………2分
令得:,令得:,
所以函数的单调增区间为,单调减区间为,. ……4分
(2)由(1)知,当时,;当时,,
则在为减函数,在为增函数,……………………6分
若,,则必有,不妨设,.
若证,即证,只需证:
即需证:,设,,………………8分
即在上恒成立,即
设,
,………………………………………10分
∴是上的增函数,故
∴是上是减函数,故,所以原命题成立.…………12分
理科数学试卷
考试时间:120分钟 分值:150分
选择题(本大题共12小题,共60分)
1.若复数的共辄复数为且满足,则复数的虚部为( )
A. B. C. D.
2. 展开式中,的系数为( )
A.126 B.-84 C.84 D.-126
3.下列说法中正确的是( )
A.若一组数据1,,3的平均数是2,则该组数据的方差是
B.线性回归直线不一定过样本中心点
C.若两个随机变量的线性相关越强,则相关系数的值越接近于1
D.先把高三年级的2000名学生编号:1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为,然后抽取编号为+50,+100,+150,……的学生,这样的抽样方法是分层抽样
4.甲、乙、丙三个同学在看,,三位运动员进行“乒乓球冠军争夺赛”赛前,对于谁会得冠军进行预测,甲说:不是,是;乙说:不是,是;丙说:不是,是.比赛结果表明,他们的话有一人全对,有一人对一半错一半,有一人全错,则冠军是( )
A. B. C. D.不能预测
5.若曲线在点处的切线与直线平行,则实数的值为( )
A. B. C.1 D.2
6. 用数学归纳法证明:1+++时,在第二步证明从n=k到n=k+1成立时,左边增加的项数是
A. B. C. D.
7.某班有60名学生,一次考试后数学成绩,若,则估计该班学生数学成绩在120分以上的人数为
A.10 B.9 C.8 D.7
8.函数的图象大致是( )
A. B.
C. D.
9.将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率,分别是( )
A., B., C., D.,
10.我校为弘扬中华传统中医药文化,在一块边长为的正方形空地中开辟出如图所示的总面积为的矩形中药园.图中阴影部分是宽度为的小路,中间三个矩形区域将种植益母草?板蓝根?苦参(其中两个小矩形区域形状?大小相同).中药种植的总面积为.当取得最大值时,的值为( )
A. B. C. D.
11.已知,,,则,,的大小关系为( )
A. B. C. D.
12.已知,函数,若函数恰有三个零点,则( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
13.平面内一点到直线:的距离为:.由此类比,空间中一点到平面:的距离为______.
14.如图,在边长为e(e为自然对数的底数)的正方形中随机撒一粒黄豆,则它落到阴影部分的概率为_____.
15.为庆祝中国共产党成立100周年,某校以班级为单位组织开展“走进革命老区,学习党史文化”研学游活动.该校高一年级部10个班级分别去3个革命老区开展研学游,每个班级只去1个革命老区,每个革命老区至少安排3个班级,则不同的安排方法共有_____种(用数字作答).
16.已知函数与的图象上存在关于轴对称的点,则的取值范围为_____.
三、解答题(本大题共6小题,共70分)
17.(10分)已知函数.
(1)解不等式;
(2)若的定义域为,求实数的取值范围.
18.(12分)某企业为确定下一年投入某种产品的研发费用,需了解年研发费用(单位:千万元)对年销售量(单位:千万件)的影响,统计了近10年投入的年研发费用与年销售量的数据,得到散点图如图所示:
(1)利用散点图判断,和(其中为大于0的常数)哪一个更适合作为年研发费用和年销售量的回归方程类型(只要给出判断即可,不必说明理由).
(2)对数据作出如下处理:令,,得到相关统计量的值如下表:
根据(1)的判断结果及表中数据,求关于的回归方程;
(3)已知企业年利润(单位:千万元)与的关系为(其中),根据(2)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
附:对于一组数据,,,,其回归直线的斜率和截距的最小二乘估计分别为,
19.(12分)在直角坐标系中,曲线的参数方程为(为参数).以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线的直角坐标方程;
(2)求曲线,公共点的直角坐标.
20.(12分)北京时间2021年6月17日9时22分,神舟十二号载人飞船在长征2F运载火箭的托举下,以一往无前之势冲入澄澈霄汉。时隔五年,神舟飞船再返苍穹!这也标志中国空间站建造任务再次向前迈出了一大步。为了了解某中学高三学生对此新闻事件的关注程度,从该校高三学生中随机抽取了100名学生进行调查,调查样本中有40名女生.如图是根据样本的调查结果绘制的等高条形图(阴影区域表示关注“神州十二号”的部分).
关注 没关注 合计
男
女
合计
附:
0.150 0.100 0.050 0.010 0.005
2.072 2.706 3.841 6.635 7.879
,其中
(1)完成上面的2×2列联表,并计算回答是否有95%的把握认为“对‘神州十二号’关注程度与性别有关”?
(2)若将频率视为概率,现从该中学高三的女生中随机抽取3人.记被抽取的3名女生中对“神州十二号”新闻关注的人数为随机变量,求的分布列及数学期望.
21.(12分)在平面直角坐标系中,直线的参数方程为:(为参数,),以为极点,轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为.
(1)当时,写出直线的普通方程和曲线的直角坐标方程;
(2)若点,设曲线与直线交于点,求的最小值.
22.(12分)已知函数(是自然对数的底数).
(1)求函数的单调区间;
(2)当,时,证明:.
长春市名校2020-2021学年高二下学期期末考试
理科数学答案
一、选择题
1.A 2.B 3.A 4.C 5.A 6.A
7. B 8.A 9.A 10.C 11.D 12.C
二、填空题
13. 14. 15.12600 16.
三、解答题
17.(Ⅰ)(Ⅱ)
(1)或或……………………………………………………3分
不等式的解集为 …………………………………………………………5分
(2)若的定义域为,则恒成立,即在上无解
又,的最小值为2, ……………9分
所以…………………………………………………………………………………10分
18.(1)选择回归类型;(2);(3)2.7亿元.
(1)由散点图知,选择回归类型更适合.………………………………1分
(2)对两边取对数,得,即…………………2分
由表中数据得:,
∴………4分
∴,
∴,…………………………………………………………………………………6分
∴年研发费用与年销售量的回归方程为.…………………………………7分
(3)由(2)知,,…………………………………8分
∴,
令,得,…………………………………10分
且当时,单调递增;当时,单调递减.
所以当千万元时,年利润取得最大值,且最大值为亿元.………………………………………………………………12分
答:要使年利润取最大值,预计下一年度投入2.7亿元.
19.(1);(2).
(1)由题意知,曲线的极坐标方程为,
即, ………………………………………2分
所以曲线的直角坐标方程为. ……………………………………4分
(2)曲线的参数方程为 …………………6分
所以曲线的直角坐标方程为. ………………………………………8分
由解得或
所以曲线公共点的直角坐标为.…………………………………12分
20.(1)填表见解析;有;(2)分布列见解析;期望为.
(1)列联表如下:………………………………………4分
关注 没关注 合计
男 30 30 60
女 12 28 40
合计 42 58 100
所以,
所以有95%的把握认为“对‘神州十二号’关注程度与性别有关”;…………………………6分
(2)因为随机选一个高三的女生,对此事关注的概率为,
又因为,所以随机变量的分布列为:………………………………8分
0 1 2 3
故.………………………………………12分
21.(1);;(2)
【详解】
(1)当时,直线的参数方程为:,
直线的普通方程为.………………………………2分
曲线的极坐标方程为,
,
曲线的直角坐标方程为,
即. …………………………………………………4分
(2)将直线的参数方程代入圆的直角坐标方程,
得,…………………………………………………6分
,
设是方程的两个根,
则,…………………………………………………8分
又直线过点,结合的几何意义得:
……………………………………10分
,
…………………………12分
22.(1)函数的单调增区间为,单调减区间为,;(2)证明见解析.
(1)由得,………………………2分
令得:,令得:,
所以函数的单调增区间为,单调减区间为,. ……4分
(2)由(1)知,当时,;当时,,
则在为减函数,在为增函数,……………………6分
若,,则必有,不妨设,.
若证,即证,只需证:
即需证:,设,,………………8分
即在上恒成立,即
设,
,………………………………………10分
∴是上的增函数,故
∴是上是减函数,故,所以原命题成立.…………12分
同课章节目录
