2020-2021学年黑龙江龙凤区九年级上册数学期末考试试题(word版含答案)
文档属性
| 名称 | 2020-2021学年黑龙江龙凤区九年级上册数学期末考试试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 520.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览



文档简介
2020年秋龙凤区九年级数学期末考试试题
(考试总分:120
分)
一、
单选题
(本题共计10小题,总分30分)
1.(3分)抛物线y=(x﹣2)2﹣1的顶点坐标是(
)
A.(﹣2,1)
B.(﹣2,﹣1)
C.(﹣2,1)
D.(2,﹣1)
2.(3分)抛物线y=2x2﹣1的图象经过点A(﹣3,y1),B(1,y2),C(4,y3),则y1,y2,y3大小关系是(
)
A.y1<y2<y3
B.y1<y3<y2
C.y2<y1<y3
D.y3<y2<y1
3.(3分)下列说法正确的是(
)
A.相等的圆心角所对的弧相等
B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等
D.等弧所对的弦相等
4.(3分)如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为(
)
A.3
B.4
C.5
D.6
5.(3分)在同一平面直角坐标中,直线y=ax+b与抛物线y=ax2+b的图象可能是(
)
A.
B.
C.
D.
6.(3分)在中,A,B为锐角,且有
,则这个三角形是(
)
A.
等腰三角形
B.
直角三角形
C.
钝角三角形
D.
锐角三角形
7.(3分)已知关于x的二次函数的图象与
轴交于A,B两点,且满足
.m的值(
)
A.-3或6
B.10或-6
C.-6或6
D.-6
8.(3分)如下图,在⊙O中,AB是⊙O的直径,AB=8cm,,M是AB上一动点,CM+DM的最小值是(
)
A.6cm
B.8cm
C.10cm
D.12cm
9.(3分)如上图,已知圆锥的母线长为,底面半径为,则此圆锥侧面展开图的圆心角的度数是(
)
A.
B.
C.
D.
10.(3分)如图,有一圆形纸片圆心为O,直径AB的长为2,弦BC//AD,将纸片沿BC、AD折叠,交于点O,那么阴影部分面积为(
)
A.
B.
C.
D.
二、
填空题
(本题共计10小题,总分30分)
11.(3分)若y=(m﹣1)x|m|+1﹣2x是二次函数,则m=_________.
12.(3分)把抛物线y=﹣x2+1向左平移3个单位,然后向上平移2个单位,平移后抛物线的顶点坐标为_________.
13.(3分)函数y=kx2﹣6x+3的图象与x轴有交点,则k的取值范围是_________.
14.(3分)已知⊙O的半径为5,直线AB与⊙O相交,则圆心O到直线AB距离d的取值范围是_________.
15.(3分)如图,四边形ABCD是⊙O的外切四边形,且AB=9,CD=15,则四边形ABCD的周长为_________.
16.(3分)如上图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2﹣mx+c<n的解集是_________.
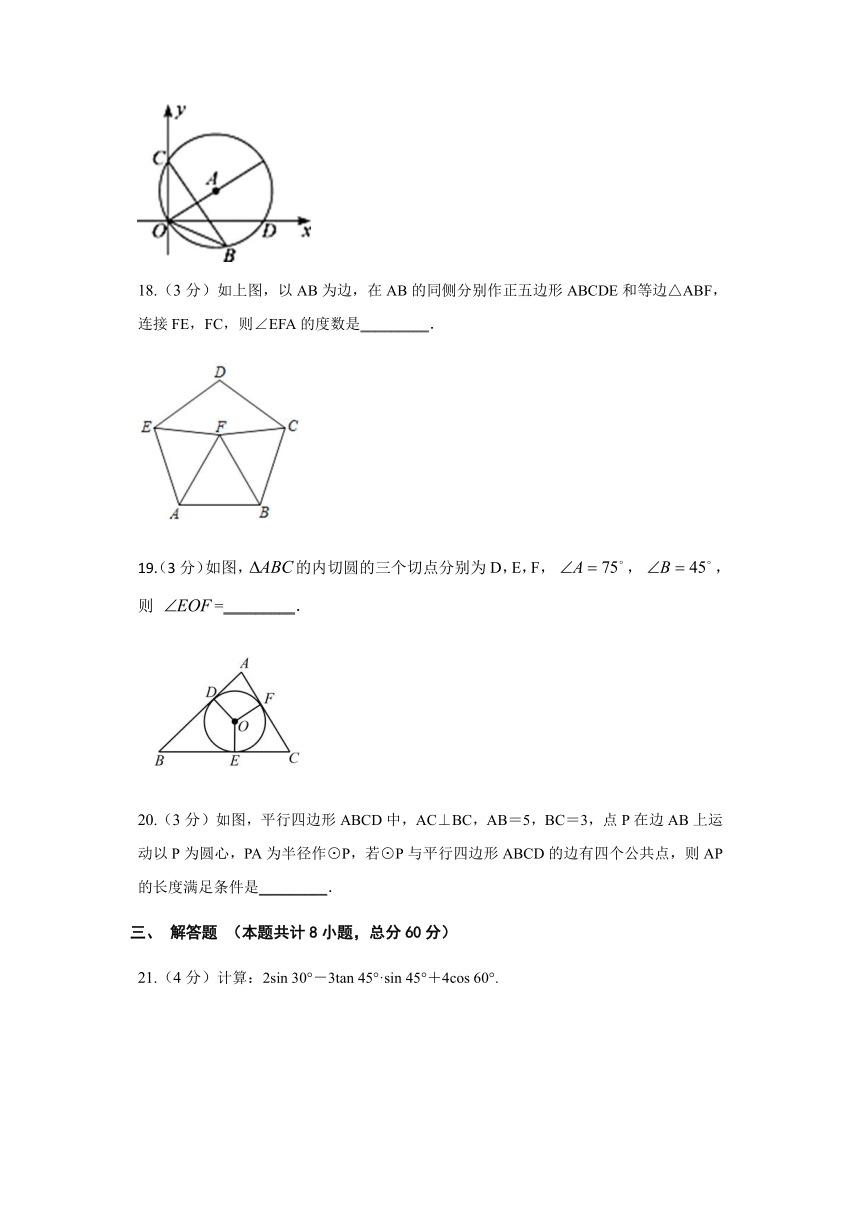
17.(3分)如下图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为_____.
18.(3分)如上图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是_________.
19.(3分)如图,的内切圆的三个切点分别为D,E,F,
,
,则
=_________.
20.(3分)如图,平行四边形ABCD中,AC⊥BC,AB=5,BC=3,点P在边AB上运动以P为圆心,PA为半径作⊙P,若⊙P与平行四边形ABCD的边有四个公共点,则AP的长度满足条件是_________.
三、
解答题
(本题共计8小题,总分60分)
21.(4分)计算:2sin
30°-3tan
45°·sin
45°+4cos
60°.
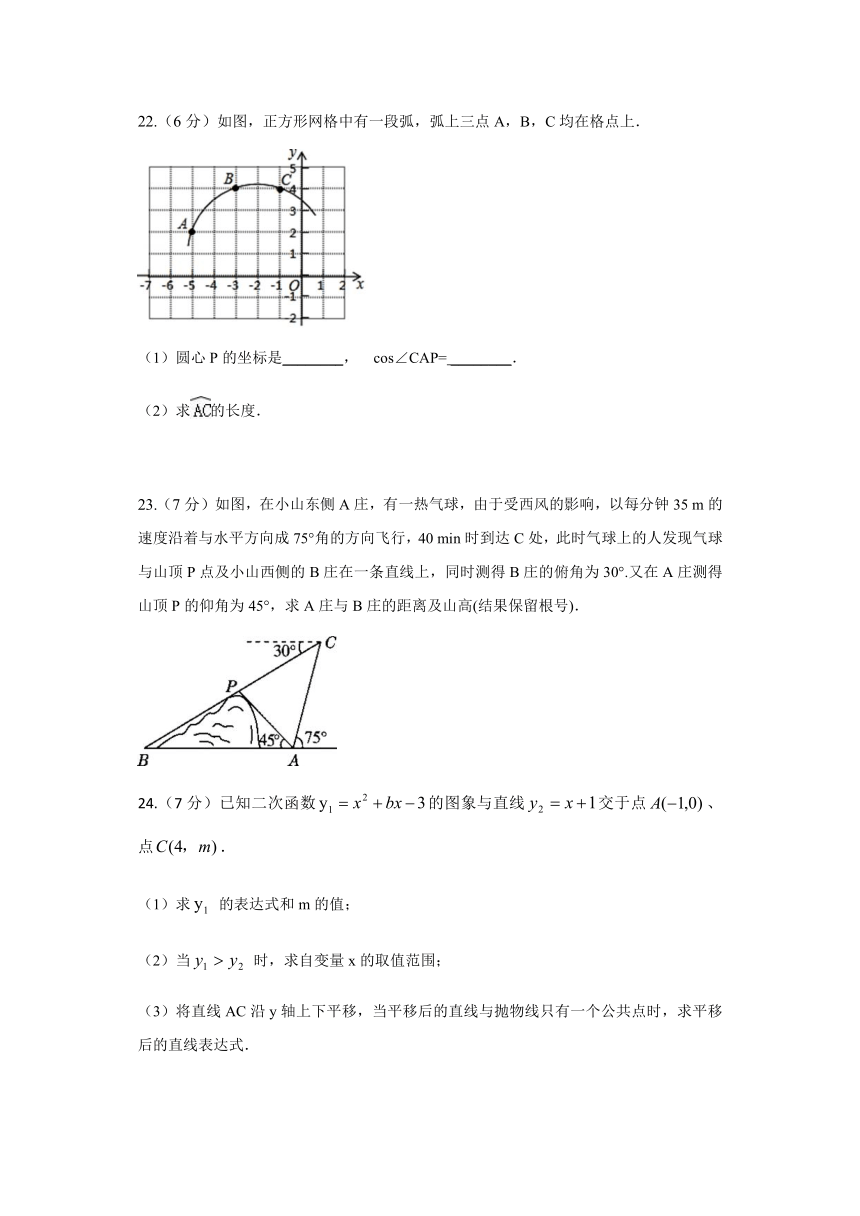
22.(6分)如图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.
(1)圆心P的坐标是________,
cos∠CAP=
________.
(2)求的长度.
23.(7分)如图,在小山东侧A庄,有一热气球,由于受西风的影响,以每分钟35
m的速度沿着与水平方向成75°角的方向飞行,40
min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(结果保留根号).
24.(7分)已知二次函数的图象与直线交于点、点.
(1)求
的表达式和m的值;
(2)当
时,求自变量x的取值范围;
(3)将直线AC沿y轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后的直线表达式.
25.(9分)新冠疫情期间,某网店销售的消毒用紫外线灯很畅销,该网店店主结合店铺数据发现,日销量y(件)是售价x(元/件)的一次函数,其售价、日销售量、日销售纯利润W(元)的四组对应值如表:
售价x(元/件)
150
160
170
180
日销售量y(件)
200
180
160
140
日销售纯利润W(元)
8000
8800
9200
9200
另外,该网店每日的固定成本折算下来为2000元.
注:日销售纯利润=日销售量×(售价﹣进价)﹣每日固定成本
(1)该商品进价是
元/件;
(2)求y关于x的函数解析式(不要求写出自变量的取值范围);
(3)当售价x(元/件)定为多少时,日销售纯利润W(元)最大,求出最大纯利润.
26.(9分)如图,在Rt△ABC中,∠C=90°,AC、BC的长恰好为方程
x2﹣14x+a=0的两根,且AC﹣BC=2.
(1)求a的值.
(2)动点P从点A出发,沿A→B的路线向点B运动(不包括端点);点Q从点B出发,沿B→C的路线向点C运动(不包括端点).若点P、Q同时出发,速度都为每秒2个单位。当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.在整个运动过程中,设△PCQ的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围和S的范围。
27.(8分)如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于点D,连接BD.
(1)求证:BD平分∠PBC;
(2)若⊙O的半径为1,PD=3DE,求OE及AB的长。
28.(10分)如图,抛物线y=﹣x2+bx+c与x轴交于点A,点B(点A在点B左侧),与y轴交于点C;直线y=x﹣3与抛物线y=﹣x2+bx+c交x轴于点B,与y轴交于点D,点D与点C关于x轴对称,点P是抛物线上的一个动点.
(1)b=___________,c=___________;
(2)当点P在第一象限时,求四边形BOCP面积的最大值,并求出此时P点的坐标;
(3)在点P的运动过程中,是否存在点P,使△BDP是以BD为直角边的直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(备用图)
答案
一、
单选题
(本题共计10小题,总分30分)
1.(3分)【答案】D
2.(3分)【答案】C
3.(3分)【答案】D
4.(3分)【答案】C
5.(3分)【答案】A
6.(3分)【答案】B
7.(3分)【答案】B
8.(3分)【答案】B
9.(3分)【答案】C
10.(3分)【答案】D
二、
填空题
(本题共计10小题,总分30分)
11.(3分)【答案】-1
12.(3分)【答案】(-3,3)
13.(3分)【答案】k≤3
14.(3分)【答案】0≤d<5
15.(3分)【答案】48
16.(3分)【答案】-117.(3分)【答案】
18.(3分)【答案】66°
19.(3分)【答案】
20.(3分)【答案】<AP<或AP=
三、
解答题
(本题共计8小题,总分60分)
21.(4分)【答案】3-
22.(6分)【答案】(1)P(﹣2,1),
cos∠CAP=;
(2)的长度为:=.
23.(7分)【答案】解:过点A作AD⊥BC,垂足为D.
在Rt△ADC中,∠ACD=75°-30°=45°,AC=35×40=1
400(m).
∴AD=AC·sin
45°=1
400×=700
(m).
在Rt△ABD中,∠B=30°,
∴AB=2AD=1
400m.-----------4分
又过点P作PE⊥AB,垂足为E,
则AE=PE,BE==PE.
∴(+1)PE=1
400.
解得PE=700(-)m.---------3分
答:A庄与B庄的距离是1
400
m,山高是700(-)m.
24.(7分)【答案】(1)
将
代入
,得到
,解得
.
故二次函数解析式为
.
代入
,得到
.
(2)
由()可得二次函数解析式
,
一次函数解析式为
,
在直角坐标系中画出两个函数图象如图:
结合图象可知当
时,
或
.
(3)
设直线
沿
轴平移
个单位,平移后的直线解析式为
,
与二次函数
只有一个交点,
故
有且只有一个解,
将方程变形得到
,
,解得
.
平移后的直线为
.
25.(9分)【答案】解:(1)100
(2)设一次函数的表达式为y=kx+b,
将点(150,200)、(160,180)代入上式得
,
解得,
故y关于x的函数解析式为y=﹣2x+500;
由题意得:
W
=y(x﹣100)﹣2000
=(﹣2x+500)(x﹣100)﹣2000
=﹣2x2+700x﹣52000,
∵﹣2<0,故W有最大值,
当x=﹣=175(元/件)时,W的最大值为9250(元);
26.(9分)【答案】解:(1)∵AC、BC的长为方程x2﹣14x+a=0的两根,
∴AC+BC=14,
又∵AC﹣BC=2,
∴AC=8,BC=6,
∴a=8×6=48;
(2)作PH⊥BC,垂足为H,
∵∠ACB=90°,
∴AB==10.
由PH∥AC得,∽
=,即=,
解得PH=(10﹣2t),
S=×CQ×PH=(6﹣2t)×(10﹣2t)=1.6t2﹣12.8t+24,
当时,
27.(8分)【答案】
28.(10分)【答案】
解:(1)b=2,
c=3
(2)连接BC,过点P作y轴的平行线交BC于点H,
由点B、C的坐标,同理可得,直线BC的表达式为y=﹣x+3,
设点P(x,﹣x2+2x+3),则点H(x,﹣x+3),
则四边形BOCP面积=S△OBC+S△PHC+S△PHB=×OB?OC+×PH×OB=3×3×3×(﹣x2+2x+3+x﹣3)=﹣x2+x+,
∵<0,故四边形BOCP面积存在最大值,
当x=时,四边形BOCP面积最大值为,此时点P(,);
(3)存在,理由:
①当∠PBD为直角时,如上图所示,
此时点P与点C重合,过点P的坐标为(0,3);
②当∠PDB为直角时,
由BD的表达式知,直线BD与x轴的倾斜角为45°,
当∠PDB为直角时,即PD⊥BD,则直线PD与x轴负半轴的夹角为45°,
故设直线PD的表达式为y=﹣x+t,
将点D的坐标代入上式得,﹣3=0+t,解得t=﹣3,
故直线PD的表达式为y=﹣x﹣3②,
联立①②并解得:x=,
故点P的坐标为(,﹣)或(,﹣),
综上,点P的坐标为(,﹣)或(,﹣)或(0,3).
(考试总分:120
分)
一、
单选题
(本题共计10小题,总分30分)
1.(3分)抛物线y=(x﹣2)2﹣1的顶点坐标是(
)
A.(﹣2,1)
B.(﹣2,﹣1)
C.(﹣2,1)
D.(2,﹣1)
2.(3分)抛物线y=2x2﹣1的图象经过点A(﹣3,y1),B(1,y2),C(4,y3),则y1,y2,y3大小关系是(
)
A.y1<y2<y3
B.y1<y3<y2
C.y2<y1<y3
D.y3<y2<y1
3.(3分)下列说法正确的是(
)
A.相等的圆心角所对的弧相等
B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等
D.等弧所对的弦相等
4.(3分)如图,⊙O中,OD⊥AB于点C,OB=13,AB=24,则OC的长为(
)
A.3
B.4
C.5
D.6
5.(3分)在同一平面直角坐标中,直线y=ax+b与抛物线y=ax2+b的图象可能是(
)
A.
B.
C.
D.
6.(3分)在中,A,B为锐角,且有
,则这个三角形是(
)
A.
等腰三角形
B.
直角三角形
C.
钝角三角形
D.
锐角三角形
7.(3分)已知关于x的二次函数的图象与
轴交于A,B两点,且满足
.m的值(
)
A.-3或6
B.10或-6
C.-6或6
D.-6
8.(3分)如下图,在⊙O中,AB是⊙O的直径,AB=8cm,,M是AB上一动点,CM+DM的最小值是(
)
A.6cm
B.8cm
C.10cm
D.12cm
9.(3分)如上图,已知圆锥的母线长为,底面半径为,则此圆锥侧面展开图的圆心角的度数是(
)
A.
B.
C.
D.
10.(3分)如图,有一圆形纸片圆心为O,直径AB的长为2,弦BC//AD,将纸片沿BC、AD折叠,交于点O,那么阴影部分面积为(
)
A.
B.
C.
D.
二、
填空题
(本题共计10小题,总分30分)
11.(3分)若y=(m﹣1)x|m|+1﹣2x是二次函数,则m=_________.
12.(3分)把抛物线y=﹣x2+1向左平移3个单位,然后向上平移2个单位,平移后抛物线的顶点坐标为_________.
13.(3分)函数y=kx2﹣6x+3的图象与x轴有交点,则k的取值范围是_________.
14.(3分)已知⊙O的半径为5,直线AB与⊙O相交,则圆心O到直线AB距离d的取值范围是_________.
15.(3分)如图,四边形ABCD是⊙O的外切四边形,且AB=9,CD=15,则四边形ABCD的周长为_________.
16.(3分)如上图,抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),B(3,q)两点,则不等式ax2﹣mx+c<n的解集是_________.
17.(3分)如下图,直径为10的⊙A经过点C(0,6)和点O(0,0),与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos∠OBC的值为_____.
18.(3分)如上图,以AB为边,在AB的同侧分别作正五边形ABCDE和等边△ABF,连接FE,FC,则∠EFA的度数是_________.
19.(3分)如图,的内切圆的三个切点分别为D,E,F,
,
,则
=_________.
20.(3分)如图,平行四边形ABCD中,AC⊥BC,AB=5,BC=3,点P在边AB上运动以P为圆心,PA为半径作⊙P,若⊙P与平行四边形ABCD的边有四个公共点,则AP的长度满足条件是_________.
三、
解答题
(本题共计8小题,总分60分)
21.(4分)计算:2sin
30°-3tan
45°·sin
45°+4cos
60°.
22.(6分)如图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.
(1)圆心P的坐标是________,
cos∠CAP=
________.
(2)求的长度.
23.(7分)如图,在小山东侧A庄,有一热气球,由于受西风的影响,以每分钟35
m的速度沿着与水平方向成75°角的方向飞行,40
min时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30°.又在A庄测得山顶P的仰角为45°,求A庄与B庄的距离及山高(结果保留根号).
24.(7分)已知二次函数的图象与直线交于点、点.
(1)求
的表达式和m的值;
(2)当
时,求自变量x的取值范围;
(3)将直线AC沿y轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后的直线表达式.
25.(9分)新冠疫情期间,某网店销售的消毒用紫外线灯很畅销,该网店店主结合店铺数据发现,日销量y(件)是售价x(元/件)的一次函数,其售价、日销售量、日销售纯利润W(元)的四组对应值如表:
售价x(元/件)
150
160
170
180
日销售量y(件)
200
180
160
140
日销售纯利润W(元)
8000
8800
9200
9200
另外,该网店每日的固定成本折算下来为2000元.
注:日销售纯利润=日销售量×(售价﹣进价)﹣每日固定成本
(1)该商品进价是
元/件;
(2)求y关于x的函数解析式(不要求写出自变量的取值范围);
(3)当售价x(元/件)定为多少时,日销售纯利润W(元)最大,求出最大纯利润.
26.(9分)如图,在Rt△ABC中,∠C=90°,AC、BC的长恰好为方程
x2﹣14x+a=0的两根,且AC﹣BC=2.
(1)求a的值.
(2)动点P从点A出发,沿A→B的路线向点B运动(不包括端点);点Q从点B出发,沿B→C的路线向点C运动(不包括端点).若点P、Q同时出发,速度都为每秒2个单位。当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.在整个运动过程中,设△PCQ的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围和S的范围。
27.(8分)如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于点D,连接BD.
(1)求证:BD平分∠PBC;
(2)若⊙O的半径为1,PD=3DE,求OE及AB的长。
28.(10分)如图,抛物线y=﹣x2+bx+c与x轴交于点A,点B(点A在点B左侧),与y轴交于点C;直线y=x﹣3与抛物线y=﹣x2+bx+c交x轴于点B,与y轴交于点D,点D与点C关于x轴对称,点P是抛物线上的一个动点.
(1)b=___________,c=___________;
(2)当点P在第一象限时,求四边形BOCP面积的最大值,并求出此时P点的坐标;
(3)在点P的运动过程中,是否存在点P,使△BDP是以BD为直角边的直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(备用图)
答案
一、
单选题
(本题共计10小题,总分30分)
1.(3分)【答案】D
2.(3分)【答案】C
3.(3分)【答案】D
4.(3分)【答案】C
5.(3分)【答案】A
6.(3分)【答案】B
7.(3分)【答案】B
8.(3分)【答案】B
9.(3分)【答案】C
10.(3分)【答案】D
二、
填空题
(本题共计10小题,总分30分)
11.(3分)【答案】-1
12.(3分)【答案】(-3,3)
13.(3分)【答案】k≤3
14.(3分)【答案】0≤d<5
15.(3分)【答案】48
16.(3分)【答案】-1
18.(3分)【答案】66°
19.(3分)【答案】
20.(3分)【答案】<AP<或AP=
三、
解答题
(本题共计8小题,总分60分)
21.(4分)【答案】3-
22.(6分)【答案】(1)P(﹣2,1),
cos∠CAP=;
(2)的长度为:=.
23.(7分)【答案】解:过点A作AD⊥BC,垂足为D.
在Rt△ADC中,∠ACD=75°-30°=45°,AC=35×40=1
400(m).
∴AD=AC·sin
45°=1
400×=700
(m).
在Rt△ABD中,∠B=30°,
∴AB=2AD=1
400m.-----------4分
又过点P作PE⊥AB,垂足为E,
则AE=PE,BE==PE.
∴(+1)PE=1
400.
解得PE=700(-)m.---------3分
答:A庄与B庄的距离是1
400
m,山高是700(-)m.
24.(7分)【答案】(1)
将
代入
,得到
,解得
.
故二次函数解析式为
.
代入
,得到
.
(2)
由()可得二次函数解析式
,
一次函数解析式为
,
在直角坐标系中画出两个函数图象如图:
结合图象可知当
时,
或
.
(3)
设直线
沿
轴平移
个单位,平移后的直线解析式为
,
与二次函数
只有一个交点,
故
有且只有一个解,
将方程变形得到
,
,解得
.
平移后的直线为
.
25.(9分)【答案】解:(1)100
(2)设一次函数的表达式为y=kx+b,
将点(150,200)、(160,180)代入上式得
,
解得,
故y关于x的函数解析式为y=﹣2x+500;
由题意得:
W
=y(x﹣100)﹣2000
=(﹣2x+500)(x﹣100)﹣2000
=﹣2x2+700x﹣52000,
∵﹣2<0,故W有最大值,
当x=﹣=175(元/件)时,W的最大值为9250(元);
26.(9分)【答案】解:(1)∵AC、BC的长为方程x2﹣14x+a=0的两根,
∴AC+BC=14,
又∵AC﹣BC=2,
∴AC=8,BC=6,
∴a=8×6=48;
(2)作PH⊥BC,垂足为H,
∵∠ACB=90°,
∴AB==10.
由PH∥AC得,∽
=,即=,
解得PH=(10﹣2t),
S=×CQ×PH=(6﹣2t)×(10﹣2t)=1.6t2﹣12.8t+24,
当时,
27.(8分)【答案】
28.(10分)【答案】
解:(1)b=2,
c=3
(2)连接BC,过点P作y轴的平行线交BC于点H,
由点B、C的坐标,同理可得,直线BC的表达式为y=﹣x+3,
设点P(x,﹣x2+2x+3),则点H(x,﹣x+3),
则四边形BOCP面积=S△OBC+S△PHC+S△PHB=×OB?OC+×PH×OB=3×3×3×(﹣x2+2x+3+x﹣3)=﹣x2+x+,
∵<0,故四边形BOCP面积存在最大值,
当x=时,四边形BOCP面积最大值为,此时点P(,);
(3)存在,理由:
①当∠PBD为直角时,如上图所示,
此时点P与点C重合,过点P的坐标为(0,3);
②当∠PDB为直角时,
由BD的表达式知,直线BD与x轴的倾斜角为45°,
当∠PDB为直角时,即PD⊥BD,则直线PD与x轴负半轴的夹角为45°,
故设直线PD的表达式为y=﹣x+t,
将点D的坐标代入上式得,﹣3=0+t,解得t=﹣3,
故直线PD的表达式为y=﹣x﹣3②,
联立①②并解得:x=,
故点P的坐标为(,﹣)或(,﹣),
综上,点P的坐标为(,﹣)或(,﹣)或(0,3).
同课章节目录
