4.5.3函数模型的应用-【新教材】人教A版(2019)高中数学必修第一册练习(Word含解析)
文档属性
| 名称 | 4.5.3函数模型的应用-【新教材】人教A版(2019)高中数学必修第一册练习(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 69.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 15:43:53 | ||
图片预览



文档简介
函数模型的应用同步练习
一、选择题
尽管目前人类还无法准确预报地震,但科学家通过研究发现地震释放出的能量E(单位:焦耳)与地震里氏震级M之间的关系为lgE=4.8+1.5M,1976年7月28日我国唐山发生的里氏7.8级地震与2008年5月12日我国汶川发生的里氏8.0级地震所释放出来的能量的比值为( )
A. 100.3 B. 0.3 C. lg1.3 D. 10?0.3
设光线通过一块玻璃,强度损失10%、如果光线原来的强度为k(k>0),通过x块这样的玻璃以后强度为y,则y=k?0.9x(x∈N?),那么光线强度减弱到原来的13以下时,至少通过这样的玻璃块数为( )参考数据:1g3≈0.477)
A. 9 B. 10 C. 11 D. 12
某数学小组进行社会实践调查,了解到鑫鑫桶装水经营部在为定价发愁.进一步调研了解到如下信息;该经营部每天的房租,人工工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表:
销售单价/元
6
7
8
9
10
11
12
日均销售量/桶
480
440
400
360
320
280
240
根据以上信息,你认为该经营部的定价为多少才能获得最大利润?( )
A. 每桶8.5元 B. 每桶9.5元 C. 每桶10.5元 D. 每桶11.5元
某市生产总值连续两年持续增加,第一年的增长率为p,第二年的增长率为q,则该市这两年生产总值的年平均增长率为( )
A. p+q2 B. 1+p1+q?12
C. pq D. 1+p1+q?1
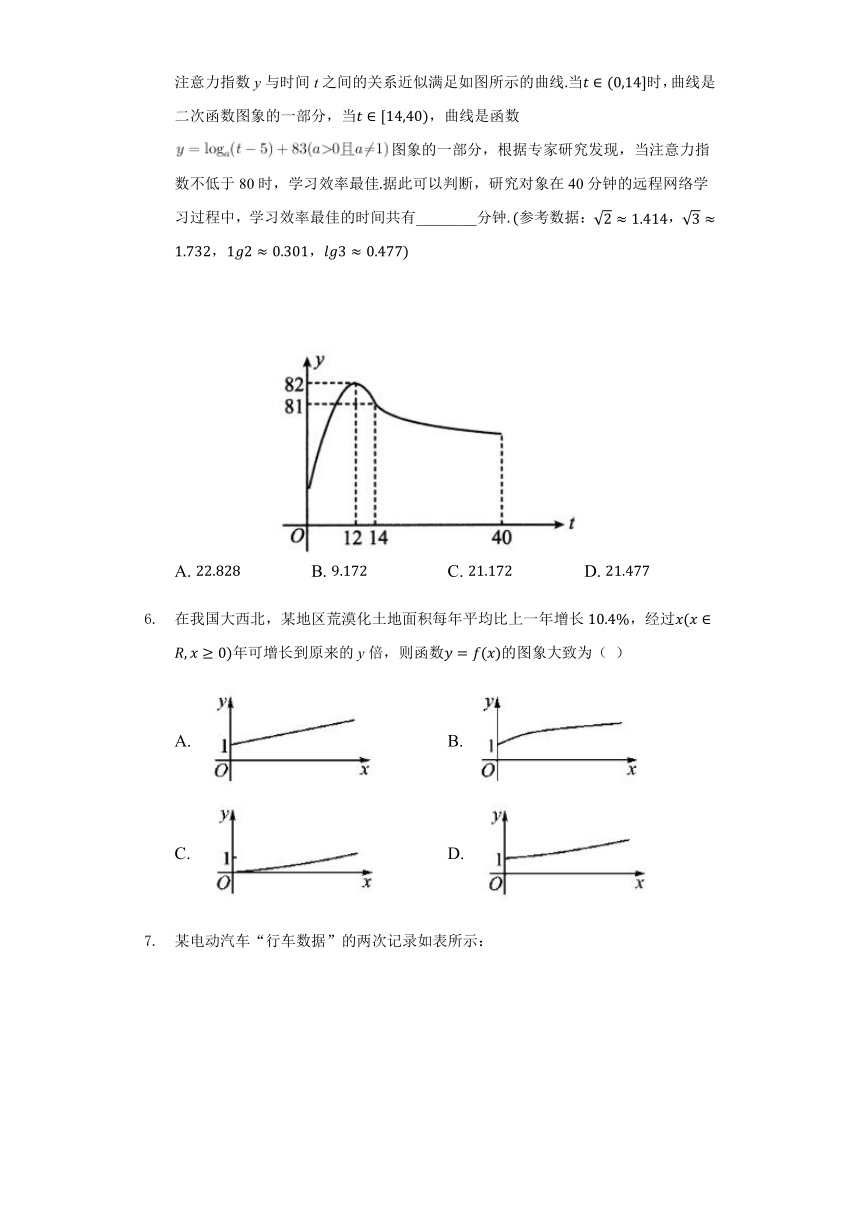
为了研究中学生远程网络学习的学习效率,某研究小组将学习注意力的集中情况用注意力指数进行量化,通过调查研究发现研究对象在40分钟的远程网络学习中,注意力指数y与时间t之间的关系近似满足如图所示的曲线.当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈[14,40),曲线是函数图象的一部分,根据专家研究发现,当注意力指数不低于80时,学习效率最佳.据此可以判断,研究对象在40分钟的远程网络学习过程中,学习效率最佳的时间共有________分钟.(参考数据:2≈1.414,3≈1.732,1g2≈0.301,lg3≈0.477)
A. 22.828 B. 9.172 C. 21.172 D. 21.477
在我国大西北,某地区荒漠化土地面积每年平均比上一年增长10.4%,经过x(x∈R,x≥0)年可增长到原来的y倍,则函数y=f(x)的图象大致为( )
A. B.
C. D.
某电动汽车“行车数据”的两次记录如表所示:
记录时间
累计里程
(单位:千米)
平均耗电量(单
位:kW·?/千米)
剩余续航里程
(单位:千米)
2019年1月1日
4?000
0.125
280
2019年1月2日
4?100
0.126
146
注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,平均耗电量=累计耗电量累计里程,剩余续航里程=剩余电量平均耗电量)
下面是该车在两次记录时间段内行驶100千米的耗电量估计正确的是( )
A. 等于12.5 B. 在12.5到12.6之间
C. 等于12.6 D. 大于12.6
“里氏震级”反映的地震释放出来的能量大小的一种度量.里氏震级M地震释放的能量E(单位:焦耳)之间的关系为:M=23lgE?165.1988年云南澜沧发生地震为里氏7.6级,2008年四川汶川发生的地震为里氏8级.若云南澜沧地震与四川地震释放的能量分别为E1,E2,则E1E2的值为( )
A. 10?0.6 B. 10?0.4 C. 100.4 D. 100.6
某企业拟建造一个容器(不计厚度,长度单位:米),该容器的底部为圆柱形,高为1,底面半径为r,上部为半径为r的半球形,按照设计要求容器的体积为283π立方米.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3万元,半球形部分每平方米建造费用为4万元,则该容器的建造费用最小时,半径r的值为( )
A. 1 B. 32 C. 34 D. 2
某城市对一种售价为每件160元的电子产品征收附加税,税率为R%(即每销售100元征税R元),若年销售量为(30?52R)万件,要使附加税不少于128万元,则R的取值范围是( )
A. [4,8] B. [6,10] C. [4%,8%] D. [6%,10%]
一服装厂生产某种风衣,日产量为xx∈N件时,售价为p元/件,每天的总成本为R元,且p=160?2x,R=500+30x,要使获得的日利润不少于1300元,则x的取值范围为(??? )
A. x∈N0C. x∈N0 二、填空题
某小区有居民1000户,去年12月份总用水量为8000吨.今年开展节约用水活动,有800户安装了节水龙头,这些用户每户每月节约用水x吨,使得今年1月份该小区居民用水总量低于6000吨.则x满足的关系式为______.
某商场已按每件80元的成本购进某商品1?000件,根据市场预测,售价为每件100元时可全部售完,售价每提高1元销量就减少5件,若要获得最大利润,售价应定为每件________元.
要制作一个容积为4?m3,高为1?m的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则当底面矩形边长为_______m时,该容器的最低总造价是________(单位:元).
三、解答题
目前,我国一些高耗能低效产业(煤炭、钢铁、有色金属、炼化等)的产能过剩将严重影响生态文明建设,“去产能”将是一项重大任务.某企业从2018年开始,每年的产能比上一年减少的百分比为x(0(1)设n年后(2018年记为第1年)年产能为2017年的a倍,请用a,n表示x;
(2)若x=10%,则至少要到哪一年才能使年产能不超过2017年的25%?(参考数据:0.913≈0.254,0.914≈0.228)
汽车保险公司每年向顾客收500元的保险费,公司通过调查历史档案知道,每年约8%的顾客要求索赔,而平均赔款额为1200元.公司每年从每位顾客那里得到的平均收益是多少?
某市自来水厂向全市生产与生活供水,蓄水池(蓄量足够大)在每天凌晨0点时将会有水15千吨,水厂每小时向池中注水2千吨,同时从池中向全市供水,若已知x(0≤x≤24)小时内供水总量为10x千吨,且当蓄水量少于3千吨时,供水就会出现紧张现象.
(Ⅰ)一天内将在哪个时间段内出现供水紧张现象?
(Ⅱ)若将每小时向池内注水2千吨改为每小时向池内注水a(a>2)千吨,求a的最小值,使得供水紧张现象消除.
答案和解析
1.D
解:设汶川地震所释放出的能量是E1,唐山地震所释放出的能量是E2,
则lgE1=4.8+1.5×7.8=16.5,lgE2=4.8+1.5×8=16.8,
∴E1=1016.5,E2=1016.8;
∴E1E2═10?0.3.
2.C
解:设通过这样的玻璃x块,则由题意得k?0.9x0),化得0.9x<13,
两边同时取常用对数,可得xlg0.9因为lg0.9<0,所以x>lg13lg0.9=?lg32lg3?1≈?0.477?0.046≈10.37,
则至少通过11块玻璃,
3.D
解:根据表格可知:销售单价每增加1元,日均销售就减少40桶.
设每桶水的价格为(6+x)元,公司日利润y元,
则:y=(6+x?5)(480?40x)?200,
=?40x2+440x+280,
∵?40<0,
∴当x=5.5时函数y有最大值,
因此,每桶水的价格为11.5元,公司日利润最大,
4.D
解:设年平均增长率为x,
则有1+p1+q=1+x2,
解得x=1+p1+q?1.
5.A
解:当t∈(0,14]时,设y=m(x?12)2+82,
将点(14,81)代入函数解析式得到4m+82=81,解得m=?14,
所以y=?14(x?12)2+82,令?14(x?12)2+82≥80,
解得:12?22≤m≤12+22,
又t∈(0,14],所以12?22≤t≤14.
将(14,81)代入函数解得a=13,
所以,令,解得:t≤32,即14所以12?22≤t≤32,
所以学习效率最佳的时间共有32?(12?22)=20+22≈22.828?.
故选A.
6.D
解:由题意可得y=(1+10.4%)x.
7.D
解:4?100×0.126?4?000×0.125=516.6?500=16.6.
8.A
解:∵云南澜沧发生地震为里氏7.6级,∴7.6=23lgE1?165,即23lgE1=7.6+165=545;①
∵四川汶川发生的地震为里氏8级,∴8=23lgE2?165,即23lgE2=8+165=565.②
①?②得:23(lgE1?lgE2)=545?565=?25,即lgE1E2=?35,
∴E1E2=10?0.6.
9.C
解:由题意知V=πr2l+12×43πr3=πr2l+23πr3=283π,
故l=V?23πr3πr2=283π?23πr3πr2=283r2?23r=28?2r33r2,
由l>0可知r<314.
∴建造费用y=(2πrl+πr2)×3+12×4πr2×4=6πr×28?2r33r2+11πr2=56πr+7πr2,(0则y′=14πr?56πr2=14π(r3?4)r2.
当r∈(0,34)时,y′<0,r∈(34,314)时,y′>0.
当r=34时,该容器的建造费用最小.
10.A解:根据题意,要使附加税不少于128万元,需30?52R×160×R%≥128,
整理得R2?12R+32≤0,解得4≤R≤8,
因此,实数R的取值范围是4,8.
11.D
解:设日利润为y元,则y=160?2x?x?500+30x=?2x2+130x?500,
由y?1300,解得20?x?45,即x的取值范围为x∈N20?x?45.
x>52
解:1000户居民去年12月份总用水量为8000吨,
则1户居民去年12月份的用水量为80001000=8吨.
1户居民安装了节水龙头后一个月的用水量为(8?x)吨,
则今年1月份该小区居民用水总量为(8?x)×800+8×200.
∴(8?x)×800+8×200<6000,解得x>52.
∴x满足的关系式为x>52.
解:设售价提高x元,获得的利润为y元,
则依题意y=(1000?5x)×(20+x)
=?5x2+900x+20000
=?5(x?90)2+60?500.
∵0<1000?5x≤1000,∴0≤x<200,
故当x=90时,ymax=60500,
此时售价为每件190元.
14.2;160
解:设底面矩形的一边长为x,由容器的容积为4?m3,高为1?m得,另一边长为4x?m.
记容器的总造价为y元,则
y=4×20+2x+4x×1×10=80+20x+4x≥80+20×2x·4x=160(元),
当且仅当x=4x,即x=2时,等号成立.
因此,当x=2时,y取得最小值160元,
即容器的最低总造价为160元.
故答案为2;160.
15.解:(1)设2017年的产能为1.
依题意得(1?x)n=a,1?x=na,x=1?nan∈N+.
(2)设m年后年产能不超过2017年的25%,则(1?10%)m≤25%,即910m≤14,
因为(910)13>14,(910)14<14,且m∈N?,
所以m的最小值为14,即至少要到2031年才能使年产能不超过2017年的25%.
16.解:设顾客人数为x,总额为500x,
索赔人数为8%?x,索赔金额为8%?x?1200=96x元,
则公司每年从每位顾客那里得到的平均收益是500x?96xx=404元.
17.解:(I)设x小时后的蓄水池水量为y千吨,则y=15+2x?10x(0≤x≤24),
当供水出现紧张现象时,y<3,即15+2x?10x<3,
解得:2∴一天内将在4点到9点时间段内出现供水紧张现象.
(II)设x小时后的水池蓄水量关于x的函数为f(x),则f(x)=15+ax?10x(0≤x≤24),
若无供水紧张现象,则f(x)≥3在[0,24]上恒成立,
∴a≥10x?12x在(0,24]上恒成立,
设g(x)=10x?12x(0∴当00,当14425∴g(x)在(0,14425)上单调递增,在(14425,24]上单调递减,
∴当x=14425时,g(x)取得最大值g(14425)=2512.
∴a的最小值为2512.
一、选择题
尽管目前人类还无法准确预报地震,但科学家通过研究发现地震释放出的能量E(单位:焦耳)与地震里氏震级M之间的关系为lgE=4.8+1.5M,1976年7月28日我国唐山发生的里氏7.8级地震与2008年5月12日我国汶川发生的里氏8.0级地震所释放出来的能量的比值为( )
A. 100.3 B. 0.3 C. lg1.3 D. 10?0.3
设光线通过一块玻璃,强度损失10%、如果光线原来的强度为k(k>0),通过x块这样的玻璃以后强度为y,则y=k?0.9x(x∈N?),那么光线强度减弱到原来的13以下时,至少通过这样的玻璃块数为( )参考数据:1g3≈0.477)
A. 9 B. 10 C. 11 D. 12
某数学小组进行社会实践调查,了解到鑫鑫桶装水经营部在为定价发愁.进一步调研了解到如下信息;该经营部每天的房租,人工工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如表:
销售单价/元
6
7
8
9
10
11
12
日均销售量/桶
480
440
400
360
320
280
240
根据以上信息,你认为该经营部的定价为多少才能获得最大利润?( )
A. 每桶8.5元 B. 每桶9.5元 C. 每桶10.5元 D. 每桶11.5元
某市生产总值连续两年持续增加,第一年的增长率为p,第二年的增长率为q,则该市这两年生产总值的年平均增长率为( )
A. p+q2 B. 1+p1+q?12
C. pq D. 1+p1+q?1
为了研究中学生远程网络学习的学习效率,某研究小组将学习注意力的集中情况用注意力指数进行量化,通过调查研究发现研究对象在40分钟的远程网络学习中,注意力指数y与时间t之间的关系近似满足如图所示的曲线.当t∈(0,14]时,曲线是二次函数图象的一部分,当t∈[14,40),曲线是函数图象的一部分,根据专家研究发现,当注意力指数不低于80时,学习效率最佳.据此可以判断,研究对象在40分钟的远程网络学习过程中,学习效率最佳的时间共有________分钟.(参考数据:2≈1.414,3≈1.732,1g2≈0.301,lg3≈0.477)
A. 22.828 B. 9.172 C. 21.172 D. 21.477
在我国大西北,某地区荒漠化土地面积每年平均比上一年增长10.4%,经过x(x∈R,x≥0)年可增长到原来的y倍,则函数y=f(x)的图象大致为( )
A. B.
C. D.
某电动汽车“行车数据”的两次记录如表所示:
记录时间
累计里程
(单位:千米)
平均耗电量(单
位:kW·?/千米)
剩余续航里程
(单位:千米)
2019年1月1日
4?000
0.125
280
2019年1月2日
4?100
0.126
146
注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,平均耗电量=累计耗电量累计里程,剩余续航里程=剩余电量平均耗电量)
下面是该车在两次记录时间段内行驶100千米的耗电量估计正确的是( )
A. 等于12.5 B. 在12.5到12.6之间
C. 等于12.6 D. 大于12.6
“里氏震级”反映的地震释放出来的能量大小的一种度量.里氏震级M地震释放的能量E(单位:焦耳)之间的关系为:M=23lgE?165.1988年云南澜沧发生地震为里氏7.6级,2008年四川汶川发生的地震为里氏8级.若云南澜沧地震与四川地震释放的能量分别为E1,E2,则E1E2的值为( )
A. 10?0.6 B. 10?0.4 C. 100.4 D. 100.6
某企业拟建造一个容器(不计厚度,长度单位:米),该容器的底部为圆柱形,高为1,底面半径为r,上部为半径为r的半球形,按照设计要求容器的体积为283π立方米.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3万元,半球形部分每平方米建造费用为4万元,则该容器的建造费用最小时,半径r的值为( )
A. 1 B. 32 C. 34 D. 2
某城市对一种售价为每件160元的电子产品征收附加税,税率为R%(即每销售100元征税R元),若年销售量为(30?52R)万件,要使附加税不少于128万元,则R的取值范围是( )
A. [4,8] B. [6,10] C. [4%,8%] D. [6%,10%]
一服装厂生产某种风衣,日产量为xx∈N件时,售价为p元/件,每天的总成本为R元,且p=160?2x,R=500+30x,要使获得的日利润不少于1300元,则x的取值范围为(??? )
A. x∈N0
某小区有居民1000户,去年12月份总用水量为8000吨.今年开展节约用水活动,有800户安装了节水龙头,这些用户每户每月节约用水x吨,使得今年1月份该小区居民用水总量低于6000吨.则x满足的关系式为______.
某商场已按每件80元的成本购进某商品1?000件,根据市场预测,售价为每件100元时可全部售完,售价每提高1元销量就减少5件,若要获得最大利润,售价应定为每件________元.
要制作一个容积为4?m3,高为1?m的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则当底面矩形边长为_______m时,该容器的最低总造价是________(单位:元).
三、解答题
目前,我国一些高耗能低效产业(煤炭、钢铁、有色金属、炼化等)的产能过剩将严重影响生态文明建设,“去产能”将是一项重大任务.某企业从2018年开始,每年的产能比上一年减少的百分比为x(0
(2)若x=10%,则至少要到哪一年才能使年产能不超过2017年的25%?(参考数据:0.913≈0.254,0.914≈0.228)
汽车保险公司每年向顾客收500元的保险费,公司通过调查历史档案知道,每年约8%的顾客要求索赔,而平均赔款额为1200元.公司每年从每位顾客那里得到的平均收益是多少?
某市自来水厂向全市生产与生活供水,蓄水池(蓄量足够大)在每天凌晨0点时将会有水15千吨,水厂每小时向池中注水2千吨,同时从池中向全市供水,若已知x(0≤x≤24)小时内供水总量为10x千吨,且当蓄水量少于3千吨时,供水就会出现紧张现象.
(Ⅰ)一天内将在哪个时间段内出现供水紧张现象?
(Ⅱ)若将每小时向池内注水2千吨改为每小时向池内注水a(a>2)千吨,求a的最小值,使得供水紧张现象消除.
答案和解析
1.D
解:设汶川地震所释放出的能量是E1,唐山地震所释放出的能量是E2,
则lgE1=4.8+1.5×7.8=16.5,lgE2=4.8+1.5×8=16.8,
∴E1=1016.5,E2=1016.8;
∴E1E2═10?0.3.
2.C
解:设通过这样的玻璃x块,则由题意得k?0.9x
两边同时取常用对数,可得xlg0.9
则至少通过11块玻璃,
3.D
解:根据表格可知:销售单价每增加1元,日均销售就减少40桶.
设每桶水的价格为(6+x)元,公司日利润y元,
则:y=(6+x?5)(480?40x)?200,
=?40x2+440x+280,
∵?40<0,
∴当x=5.5时函数y有最大值,
因此,每桶水的价格为11.5元,公司日利润最大,
4.D
解:设年平均增长率为x,
则有1+p1+q=1+x2,
解得x=1+p1+q?1.
5.A
解:当t∈(0,14]时,设y=m(x?12)2+82,
将点(14,81)代入函数解析式得到4m+82=81,解得m=?14,
所以y=?14(x?12)2+82,令?14(x?12)2+82≥80,
解得:12?22≤m≤12+22,
又t∈(0,14],所以12?22≤t≤14.
将(14,81)代入函数解得a=13,
所以,令,解得:t≤32,即14
所以学习效率最佳的时间共有32?(12?22)=20+22≈22.828?.
故选A.
6.D
解:由题意可得y=(1+10.4%)x.
7.D
解:4?100×0.126?4?000×0.125=516.6?500=16.6.
8.A
解:∵云南澜沧发生地震为里氏7.6级,∴7.6=23lgE1?165,即23lgE1=7.6+165=545;①
∵四川汶川发生的地震为里氏8级,∴8=23lgE2?165,即23lgE2=8+165=565.②
①?②得:23(lgE1?lgE2)=545?565=?25,即lgE1E2=?35,
∴E1E2=10?0.6.
9.C
解:由题意知V=πr2l+12×43πr3=πr2l+23πr3=283π,
故l=V?23πr3πr2=283π?23πr3πr2=283r2?23r=28?2r33r2,
由l>0可知r<314.
∴建造费用y=(2πrl+πr2)×3+12×4πr2×4=6πr×28?2r33r2+11πr2=56πr+7πr2,(0
当r∈(0,34)时,y′<0,r∈(34,314)时,y′>0.
当r=34时,该容器的建造费用最小.
10.A解:根据题意,要使附加税不少于128万元,需30?52R×160×R%≥128,
整理得R2?12R+32≤0,解得4≤R≤8,
因此,实数R的取值范围是4,8.
11.D
解:设日利润为y元,则y=160?2x?x?500+30x=?2x2+130x?500,
由y?1300,解得20?x?45,即x的取值范围为x∈N20?x?45.
x>52
解:1000户居民去年12月份总用水量为8000吨,
则1户居民去年12月份的用水量为80001000=8吨.
1户居民安装了节水龙头后一个月的用水量为(8?x)吨,
则今年1月份该小区居民用水总量为(8?x)×800+8×200.
∴(8?x)×800+8×200<6000,解得x>52.
∴x满足的关系式为x>52.
解:设售价提高x元,获得的利润为y元,
则依题意y=(1000?5x)×(20+x)
=?5x2+900x+20000
=?5(x?90)2+60?500.
∵0<1000?5x≤1000,∴0≤x<200,
故当x=90时,ymax=60500,
此时售价为每件190元.
14.2;160
解:设底面矩形的一边长为x,由容器的容积为4?m3,高为1?m得,另一边长为4x?m.
记容器的总造价为y元,则
y=4×20+2x+4x×1×10=80+20x+4x≥80+20×2x·4x=160(元),
当且仅当x=4x,即x=2时,等号成立.
因此,当x=2时,y取得最小值160元,
即容器的最低总造价为160元.
故答案为2;160.
15.解:(1)设2017年的产能为1.
依题意得(1?x)n=a,1?x=na,x=1?nan∈N+.
(2)设m年后年产能不超过2017年的25%,则(1?10%)m≤25%,即910m≤14,
因为(910)13>14,(910)14<14,且m∈N?,
所以m的最小值为14,即至少要到2031年才能使年产能不超过2017年的25%.
16.解:设顾客人数为x,总额为500x,
索赔人数为8%?x,索赔金额为8%?x?1200=96x元,
则公司每年从每位顾客那里得到的平均收益是500x?96xx=404元.
17.解:(I)设x小时后的蓄水池水量为y千吨,则y=15+2x?10x(0≤x≤24),
当供水出现紧张现象时,y<3,即15+2x?10x<3,
解得:2
(II)设x小时后的水池蓄水量关于x的函数为f(x),则f(x)=15+ax?10x(0≤x≤24),
若无供水紧张现象,则f(x)≥3在[0,24]上恒成立,
∴a≥10x?12x在(0,24]上恒成立,
设g(x)=10x?12x(0
∴当x=14425时,g(x)取得最大值g(14425)=2512.
∴a的最小值为2512.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
