广西桂林市2020-2021学年高一下学期期末质量检测数学试题 Word版含答案
文档属性
| 名称 | 广西桂林市2020-2021学年高一下学期期末质量检测数学试题 Word版含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 450.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览



文档简介
桂林市2020~2021学年度下学期期末质量检测
高一年级 数学
(考试时间120分钟,满分150分)
说明:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.请在答题卷上答题(在本试卷上答题无效)
第Ⅰ卷 选择题
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.
1.false的值等于( )
A.false B.false C.false D.false
2.已知点false,false,则向量false( )
A.false B.false C.false D.false
3.已知圆false,则其圆心的坐标为( )
A.false B.false C.false D.false
4.在空间直角坐标系中,已知false,false,那么线段false中点的坐标为( )
A.false B.false C.false D.false
5.函数false的最小正周期是( )
A.false B.false C.false D.false
6.如图,正方形false内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自正方形内白色部分的概率是( )
A.false B.false C.false D.false
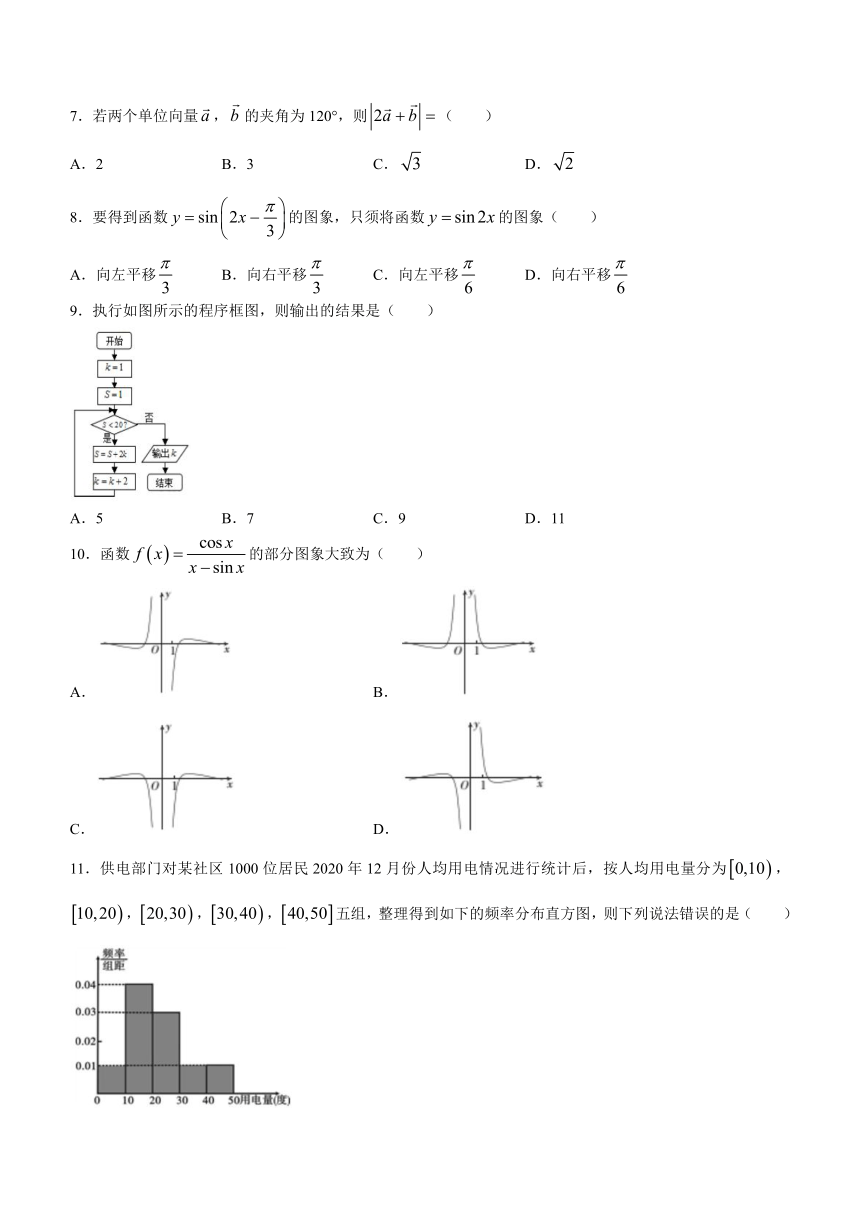
7.若两个单位向量false,false的夹角为120°,则false( )
A.2 B.3 C.false D.false
8.要得到函数false的图象,只须将函数false的图象( )
A.向左平移false B.向右平移false C.向左平移false D.向右平移false
9.执行如图所示的程序框图,则输出的结果是( )
A.5 B.7 C.9 D.11
10.函数false的部分图象大致为( )
A. B.
C. D.
11.供电部门对某社区1000位居民2020年12月份人均用电情况进行统计后,按人均用电量分为false,false,false,false,false五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
A.12月份人均用电量人数最多的一组有400人.
B.12月份人均用电量不低于20度的有500人.
C.12月份人均用电量为25度.
D.在这1000位居民中任选1位协助收费,选到的居民用电量在false一组的概率为false.
12.由直线false上的点向圆false引切线,则切线长的最小值为( )
A.false B.3 C.false D.false
第Ⅱ卷 非选择题
二、填空题:本大题共4小题,每小题5分,共20分.
13.若向量false,false,则false______.
14.若角false是第二象限的角,且false,则false______.
15.在false中,false,false,false,false为false边上的高,false为false的中点,若false,其中false,false,则false等于______.
16.已知函数false,false,且false,对不同的false,若false,有false,则false______.
三、解答题:本大题共6小题,共70分.解答应给出文字说明、证明过程及演算步骤.
17.(本小题满分10分)
已知向量false,false.
(1)若false,求false的值;
(2)若false,求false.
18.(本小题满分12分)
已知false,false,false,false.
(1)求false的值;
(2)求false的值.
19.(本小题满分12分)
新型冠状病毒肺炎疫情期间,某医院随着医疗工作的有序开展,治愈新冠肺炎的人数逐日增加.从3月1日至5日,5天内该医院每日治愈的新型冠状病毒肺炎人数false(人)与天数false(天)之间的关系如下表:
第false天
1
2
3
4
5
人数false(人)
2
4
8
false
18
若在3月1日起的一段时间内,该医院每日治愈的新型冠状病毒肺炎病人数false与天数false具有线性相关关系,且其线性回归方程false过定点false,false,false.
(1)求false的值和线性回归方程false;
(2)预测该医院3月11日能否可以实现“单日治愈人数突破40人”的目标?
参考公式:false,false,false,false为样本平均值.
20.(本小题满分12分)
长时间使用手机上网,会严重影响学生的身体健康.某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长(小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
(1)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(2)从A班的样本数据中随机抽取一个小于21的数据记为false,从B班的样本数据中随机抽取一个小于21的数据记为false,求false的概率.
21.(本小题满分12分)
已知false.
(1)求函数false的递增区间;
(2)是否存在实数false,使得不等式false对任意false恒成立?若存在,求出false的取值范围;若不存在,说明理由.
22.(本小题满分12分)
平面直角坐标系false中,已知点false,圆false与false轴的正半轴的交于点为false.
(1)若过点false的直线false与圆false交于不同的两点false,false.线段false的中点为false,求点false的轨迹方程;
(2)设直线false,false的斜率分别是false,false,证明:false为定值.
桂林市2020~2021学年度下学期期末质量检测
高一年级数学参考答案及评分标准
一、选择题:每小题5分,本题满分共60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
A
C
B
C
D
C
D
C
A
二、填空题:每小题5分,满分20分.
13.false 14.false 15.false 16.false
三、解答题:本大题共6小题,共70分.解答应给出文字说明、证明过程或演算步骤.
17.(本题满分10分)
解:(1)false,false.
解得false.
(2)false,false.
所以false,解得false.
false.从而false.
18.(本题满分12分)
解:(1)因为false,false,所以false.
所以false,
false,
所以false.
(2)又因为false,false,
所以false.
所以false.
19.(本题满分12分)
解:(1)由题意,false,false,false,
解得false
false,false,
所以,false.
false,
所以线性回归方程为false.
(2)在false中,3月11日即false,
取false,false
false,
∴该医院3月11日能实现“单日治愈人数突破40人”的目标.
20.(本题满分12分)
解:(1)A班样本数据的平均值为false,
B班样本数据的平均值为false,
据此估计B班学生平均每周上网时间较长.
(2)依题意,从A班的样本数据中随机抽取一个小于21的数据记为false,从B班的样本数据中随机抽取一个小于21的数据记为false,则共有8种,分别为false,false,false,false,false,false,false,false.
其中满足条件“false”的共有4种,分别为false,false,false,false
设“false”为事件false,则false.
所以false的概率为false.
21.(本题满分12分)
解:(1)false,
false,
由false,
解得false,false.
所以函数false的递增区间为false.
(2)假设存在实数false满足题意,则不等式即为false,
令false,则false
则原不等式false.
又false,
由false,false.
所以false,故false
令函数false,
即false,false恒成立.
由一元二次方程根的分布,只需false.
22.(本题满分12分)
解:(1)设点false,因为false为弦false中点,所以false,
false,false,
∴由false,得false化简得false.
∴false的轨迹方程是false.
(2)由题意点false,联立false得false
设false,false,则false
false
false
false
∴false是定值.
高一年级 数学
(考试时间120分钟,满分150分)
说明:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.
2.请在答题卷上答题(在本试卷上答题无效)
第Ⅰ卷 选择题
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.
1.false的值等于( )
A.false B.false C.false D.false
2.已知点false,false,则向量false( )
A.false B.false C.false D.false
3.已知圆false,则其圆心的坐标为( )
A.false B.false C.false D.false
4.在空间直角坐标系中,已知false,false,那么线段false中点的坐标为( )
A.false B.false C.false D.false
5.函数false的最小正周期是( )
A.false B.false C.false D.false
6.如图,正方形false内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自正方形内白色部分的概率是( )
A.false B.false C.false D.false
7.若两个单位向量false,false的夹角为120°,则false( )
A.2 B.3 C.false D.false
8.要得到函数false的图象,只须将函数false的图象( )
A.向左平移false B.向右平移false C.向左平移false D.向右平移false
9.执行如图所示的程序框图,则输出的结果是( )
A.5 B.7 C.9 D.11
10.函数false的部分图象大致为( )
A. B.
C. D.
11.供电部门对某社区1000位居民2020年12月份人均用电情况进行统计后,按人均用电量分为false,false,false,false,false五组,整理得到如下的频率分布直方图,则下列说法错误的是( )
A.12月份人均用电量人数最多的一组有400人.
B.12月份人均用电量不低于20度的有500人.
C.12月份人均用电量为25度.
D.在这1000位居民中任选1位协助收费,选到的居民用电量在false一组的概率为false.
12.由直线false上的点向圆false引切线,则切线长的最小值为( )
A.false B.3 C.false D.false
第Ⅱ卷 非选择题
二、填空题:本大题共4小题,每小题5分,共20分.
13.若向量false,false,则false______.
14.若角false是第二象限的角,且false,则false______.
15.在false中,false,false,false,false为false边上的高,false为false的中点,若false,其中false,false,则false等于______.
16.已知函数false,false,且false,对不同的false,若false,有false,则false______.
三、解答题:本大题共6小题,共70分.解答应给出文字说明、证明过程及演算步骤.
17.(本小题满分10分)
已知向量false,false.
(1)若false,求false的值;
(2)若false,求false.
18.(本小题满分12分)
已知false,false,false,false.
(1)求false的值;
(2)求false的值.
19.(本小题满分12分)
新型冠状病毒肺炎疫情期间,某医院随着医疗工作的有序开展,治愈新冠肺炎的人数逐日增加.从3月1日至5日,5天内该医院每日治愈的新型冠状病毒肺炎人数false(人)与天数false(天)之间的关系如下表:
第false天
1
2
3
4
5
人数false(人)
2
4
8
false
18
若在3月1日起的一段时间内,该医院每日治愈的新型冠状病毒肺炎病人数false与天数false具有线性相关关系,且其线性回归方程false过定点false,false,false.
(1)求false的值和线性回归方程false;
(2)预测该医院3月11日能否可以实现“单日治愈人数突破40人”的目标?
参考公式:false,false,false,false为样本平均值.
20.(本小题满分12分)
长时间使用手机上网,会严重影响学生的身体健康.某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长(小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
(1)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(2)从A班的样本数据中随机抽取一个小于21的数据记为false,从B班的样本数据中随机抽取一个小于21的数据记为false,求false的概率.
21.(本小题满分12分)
已知false.
(1)求函数false的递增区间;
(2)是否存在实数false,使得不等式false对任意false恒成立?若存在,求出false的取值范围;若不存在,说明理由.
22.(本小题满分12分)
平面直角坐标系false中,已知点false,圆false与false轴的正半轴的交于点为false.
(1)若过点false的直线false与圆false交于不同的两点false,false.线段false的中点为false,求点false的轨迹方程;
(2)设直线false,false的斜率分别是false,false,证明:false为定值.
桂林市2020~2021学年度下学期期末质量检测
高一年级数学参考答案及评分标准
一、选择题:每小题5分,本题满分共60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
A
C
B
C
D
C
D
C
A
二、填空题:每小题5分,满分20分.
13.false 14.false 15.false 16.false
三、解答题:本大题共6小题,共70分.解答应给出文字说明、证明过程或演算步骤.
17.(本题满分10分)
解:(1)false,false.
解得false.
(2)false,false.
所以false,解得false.
false.从而false.
18.(本题满分12分)
解:(1)因为false,false,所以false.
所以false,
false,
所以false.
(2)又因为false,false,
所以false.
所以false.
19.(本题满分12分)
解:(1)由题意,false,false,false,
解得false
false,false,
所以,false.
false,
所以线性回归方程为false.
(2)在false中,3月11日即false,
取false,false
false,
∴该医院3月11日能实现“单日治愈人数突破40人”的目标.
20.(本题满分12分)
解:(1)A班样本数据的平均值为false,
B班样本数据的平均值为false,
据此估计B班学生平均每周上网时间较长.
(2)依题意,从A班的样本数据中随机抽取一个小于21的数据记为false,从B班的样本数据中随机抽取一个小于21的数据记为false,则共有8种,分别为false,false,false,false,false,false,false,false.
其中满足条件“false”的共有4种,分别为false,false,false,false
设“false”为事件false,则false.
所以false的概率为false.
21.(本题满分12分)
解:(1)false,
false,
由false,
解得false,false.
所以函数false的递增区间为false.
(2)假设存在实数false满足题意,则不等式即为false,
令false,则false
则原不等式false.
又false,
由false,false.
所以false,故false
令函数false,
即false,false恒成立.
由一元二次方程根的分布,只需false.
22.(本题满分12分)
解:(1)设点false,因为false为弦false中点,所以false,
false,false,
∴由false,得false化简得false.
∴false的轨迹方程是false.
(2)由题意点false,联立false得false
设false,false,则false
false
false
false
∴false是定值.
同课章节目录
