吉林省长春市二道区重点高中2020-2021学年高二下学期期末考数学(文)试题 Word版含答案
文档属性
| 名称 | 吉林省长春市二道区重点高中2020-2021学年高二下学期期末考数学(文)试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 803.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 17:58:50 | ||
图片预览


文档简介
长春市二道区重点高中2020-2021学年高二下学期期末考试
数学试卷(文)
答题时间:100 分钟 满分:150 分
一、选择题(本大题共12小题,每小题5分,共60分)
1. 设,则
A. B. C. D.
2. 已知向量,则AA
A. B. C. D.
3. 已知直线,直线,若,则
A.1 B. 0 C. D. 2
4.已知,,,大小关系正确的是
A. B. C. D.
5. 若,则
A. B. C. D.
6.已知m,n表示两条不同直线,α表示平面,下列说法正确的是
A.若m∥α,n∥α,则m∥n B.若m⊥α,n?α,则m⊥n
C.若m⊥α,m⊥n,则n∥α D.若m∥α,m⊥n,则n⊥α
7.已知数列{an}满足a1=1,an+1=2an,则a4=( )
A. 4 B. 8 C. 16 D. 32
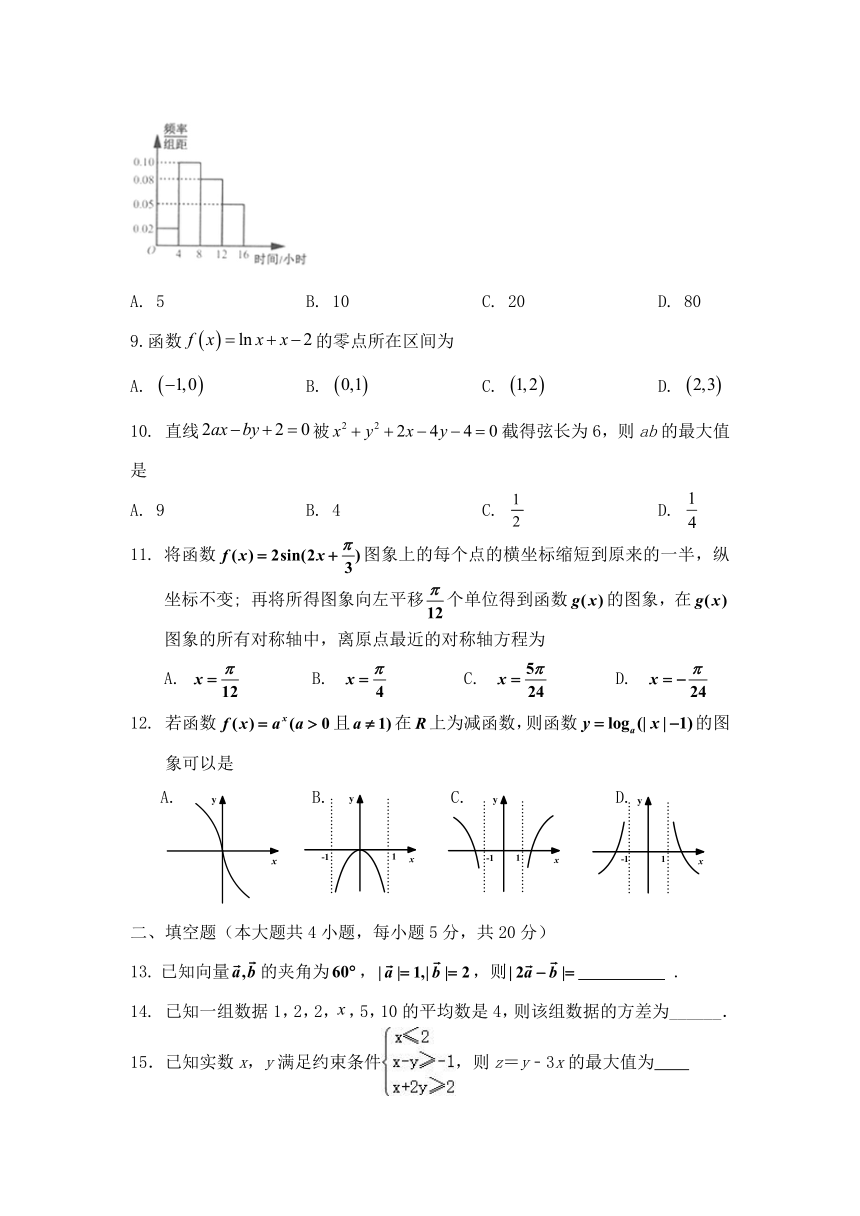
8.某学校随机抽取100名学生,调查其平均一周使用互联网的时间(单位:小时),根据调查结果制成了如图所示的频率分布直方图,其中使用时间的范围是,样本数据分组区间为.根据直方图,这100名学生中平均一周使用互联网的时间不少于12小时的人数为
A. 5 B. 10 C. 20 D. 80
9.函数的零点所在区间为
A. B. C. D.
10. 直线被截得弦长为6,则ab的最大值是
A. 9 B. 4 C. D.
11. 将函数图象上的每个点的横坐标缩短到原来的一半,纵坐标不变; 再将所得图象向左平移个单位得到函数的图象,在图象的所有对称轴中,离原点最近的对称轴方程为
A. B. C. D.
12. 若函数且在上为减函数,则函数的图象可以是
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13. 已知向量的夹角为,,则 .
14. 已知一组数据1,2,2,,5,10的平均数是4,则该组数据的方差为______.
15.已知实数x,y满足约束条件,则z=y﹣3x的最大值为
16. 三棱柱的侧棱垂直于底面,且 ,若该三棱柱的所有顶点都在同一球面上,则该球的表面积为
三、解答题(本大题共6小题,17~21题每小题13分,22题5分共70分)
17.(13分)在中,、、分别为内角、、的对边,且,
(1)求的值;
(2)若,且,求的面积。
18.(13分)已知向量a=(cosx,sinx),, .
(1)若a∥b,求x的值;
(2)记,求的最大值和最小值以及对应的x的值
19.(13分)已知数列{an}是一个公差为d(d≠0)的等差数列,前n项和为Sn,a2、a4、a5成等比数列,且S5=﹣15.
(1)求数列{an}的通项公式;
(2)求数列{}的前10项和.
20.(13分)如图,四棱锥中,侧面为等边三角形且垂直于底面,
(1)证明:直线平面;
(2)若△的面积为,求四棱锥的体积.
21.(13分)新冠肺炎疫情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从高中三个年级的学生中抽取一个容量为的样本进行关于线上教学实施情况的问卷调查. 已知该校高一年级共有学生人,高三年级共有人,抽取的样本中高二年级有人. 下表是根据抽样调查情况得到的高二学生日睡眠时间(单位:)的频率分布表.
分组 频数 频率
合计
(1)求该校高二学生的总数;
(2)求频率分布表中实数的值
(3)已知日睡眠时间在区间内的名高二学生中,有名女生,名男生,若从中任选人进行面谈,求选中的人恰好为两男一女的概率.
22.延展题(5分)
在平面直角坐标系中,以点为圆心且与直线相切的所有圆中,半径最大的圆的标准方程为______.
高二数学试卷 文科(答案)
一、选择题:
1 2 3 4 5 6 7 8 9 10 11 12
D A A C C B B C C D D D
二、填空题:
13. 2 14. 9 15. 1 16.
三、解答题:
17. 解:(1)在中,,
由正弦定理得,
即,∴,
又∵,∴,
∵,∴,;
(2)在中,由余弦定理可得,又,
∴有,即,∴。
18. 解:(1)因为,,a∥b,
所以.
若,则,与矛盾,故.
于是.
又,所以.
(2).
因为,所以,
从而.
于是,当,即时,取到最大值3;
当,即时,取到最小值.
19. 解:(1)由a2、a4、a5成等比数列得:,
即5d2=﹣a1d,
又∵d≠0,∴a1=﹣5d;
而,∴d=1;
∴an=a1+(n﹣1)d=n﹣6,∴{an}的通项公式为an=n﹣6.
(2)∵,∴,
令,则为常数,∴{cn}是首项为﹣5,公差为的等差数列,∴的前10项和为.
20. 解:(1)在平面ABCD内,因为∠BAD=∠ABC=90°,所以BC∥AD.又,,故BC∥平面PAD.
(2)去AD的中点M,学 科&网连结PM,CM,由及BC∥AD,∠ABC=90°得四边形ABCM为正方形,则CM⊥AD.
因为侧面PAD为等边三角形且垂直于底面ABCD,平面PAD∩平面ABCD=AD,所以PM⊥AD,PM⊥底面ABCD,因为,所以PM⊥CM.
设BC=x,则CM=x,CD=,PM=,PC=PD=2x.取CD的中点N,连结PN,则PN⊥CD,所以因为△PCD的面积为,所以,
解得x=-2(舍去),x=2,于是AB=BC=2,AD=4,PM=,
所以四棱锥P-ABCD的体积.
21. 解:(1)设该校高二学生的总数为,由题意,解得,所以该校高二学生总数为人.
(2)由题意,解得,
,
.
(3)记“选中的人恰好为两男一女”为事件,记名高二学生中女生为,,男生为,,,从中任选人有以下情况: ;;;;;;;;;,共种情况,基本事件共有个,它们是等可能的,
事件包含的基本事件有个,分别为:;;;;;,
故,所以选中的人恰好为两男一女的概率为.
22. 【答案】
【解析】
试题分析:因为直线恒过定点,所以圆心到直线的最大距离为,所以半径最大时的半径,所以半径最大的圆的标准方程为.
数学试卷(文)
答题时间:100 分钟 满分:150 分
一、选择题(本大题共12小题,每小题5分,共60分)
1. 设,则
A. B. C. D.
2. 已知向量,则AA
A. B. C. D.
3. 已知直线,直线,若,则
A.1 B. 0 C. D. 2
4.已知,,,大小关系正确的是
A. B. C. D.
5. 若,则
A. B. C. D.
6.已知m,n表示两条不同直线,α表示平面,下列说法正确的是
A.若m∥α,n∥α,则m∥n B.若m⊥α,n?α,则m⊥n
C.若m⊥α,m⊥n,则n∥α D.若m∥α,m⊥n,则n⊥α
7.已知数列{an}满足a1=1,an+1=2an,则a4=( )
A. 4 B. 8 C. 16 D. 32
8.某学校随机抽取100名学生,调查其平均一周使用互联网的时间(单位:小时),根据调查结果制成了如图所示的频率分布直方图,其中使用时间的范围是,样本数据分组区间为.根据直方图,这100名学生中平均一周使用互联网的时间不少于12小时的人数为
A. 5 B. 10 C. 20 D. 80
9.函数的零点所在区间为
A. B. C. D.
10. 直线被截得弦长为6,则ab的最大值是
A. 9 B. 4 C. D.
11. 将函数图象上的每个点的横坐标缩短到原来的一半,纵坐标不变; 再将所得图象向左平移个单位得到函数的图象,在图象的所有对称轴中,离原点最近的对称轴方程为
A. B. C. D.
12. 若函数且在上为减函数,则函数的图象可以是
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13. 已知向量的夹角为,,则 .
14. 已知一组数据1,2,2,,5,10的平均数是4,则该组数据的方差为______.
15.已知实数x,y满足约束条件,则z=y﹣3x的最大值为
16. 三棱柱的侧棱垂直于底面,且 ,若该三棱柱的所有顶点都在同一球面上,则该球的表面积为
三、解答题(本大题共6小题,17~21题每小题13分,22题5分共70分)
17.(13分)在中,、、分别为内角、、的对边,且,
(1)求的值;
(2)若,且,求的面积。
18.(13分)已知向量a=(cosx,sinx),, .
(1)若a∥b,求x的值;
(2)记,求的最大值和最小值以及对应的x的值
19.(13分)已知数列{an}是一个公差为d(d≠0)的等差数列,前n项和为Sn,a2、a4、a5成等比数列,且S5=﹣15.
(1)求数列{an}的通项公式;
(2)求数列{}的前10项和.
20.(13分)如图,四棱锥中,侧面为等边三角形且垂直于底面,
(1)证明:直线平面;
(2)若△的面积为,求四棱锥的体积.
21.(13分)新冠肺炎疫情期间,为确保“停课不停学”,各校精心组织了线上教学活动.开学后,某校采用分层抽样的方法从高中三个年级的学生中抽取一个容量为的样本进行关于线上教学实施情况的问卷调查. 已知该校高一年级共有学生人,高三年级共有人,抽取的样本中高二年级有人. 下表是根据抽样调查情况得到的高二学生日睡眠时间(单位:)的频率分布表.
分组 频数 频率
合计
(1)求该校高二学生的总数;
(2)求频率分布表中实数的值
(3)已知日睡眠时间在区间内的名高二学生中,有名女生,名男生,若从中任选人进行面谈,求选中的人恰好为两男一女的概率.
22.延展题(5分)
在平面直角坐标系中,以点为圆心且与直线相切的所有圆中,半径最大的圆的标准方程为______.
高二数学试卷 文科(答案)
一、选择题:
1 2 3 4 5 6 7 8 9 10 11 12
D A A C C B B C C D D D
二、填空题:
13. 2 14. 9 15. 1 16.
三、解答题:
17. 解:(1)在中,,
由正弦定理得,
即,∴,
又∵,∴,
∵,∴,;
(2)在中,由余弦定理可得,又,
∴有,即,∴。
18. 解:(1)因为,,a∥b,
所以.
若,则,与矛盾,故.
于是.
又,所以.
(2).
因为,所以,
从而.
于是,当,即时,取到最大值3;
当,即时,取到最小值.
19. 解:(1)由a2、a4、a5成等比数列得:,
即5d2=﹣a1d,
又∵d≠0,∴a1=﹣5d;
而,∴d=1;
∴an=a1+(n﹣1)d=n﹣6,∴{an}的通项公式为an=n﹣6.
(2)∵,∴,
令,则为常数,∴{cn}是首项为﹣5,公差为的等差数列,∴的前10项和为.
20. 解:(1)在平面ABCD内,因为∠BAD=∠ABC=90°,所以BC∥AD.又,,故BC∥平面PAD.
(2)去AD的中点M,学 科&网连结PM,CM,由及BC∥AD,∠ABC=90°得四边形ABCM为正方形,则CM⊥AD.
因为侧面PAD为等边三角形且垂直于底面ABCD,平面PAD∩平面ABCD=AD,所以PM⊥AD,PM⊥底面ABCD,因为,所以PM⊥CM.
设BC=x,则CM=x,CD=,PM=,PC=PD=2x.取CD的中点N,连结PN,则PN⊥CD,所以因为△PCD的面积为,所以,
解得x=-2(舍去),x=2,于是AB=BC=2,AD=4,PM=,
所以四棱锥P-ABCD的体积.
21. 解:(1)设该校高二学生的总数为,由题意,解得,所以该校高二学生总数为人.
(2)由题意,解得,
,
.
(3)记“选中的人恰好为两男一女”为事件,记名高二学生中女生为,,男生为,,,从中任选人有以下情况: ;;;;;;;;;,共种情况,基本事件共有个,它们是等可能的,
事件包含的基本事件有个,分别为:;;;;;,
故,所以选中的人恰好为两男一女的概率为.
22. 【答案】
【解析】
试题分析:因为直线恒过定点,所以圆心到直线的最大距离为,所以半径最大时的半径,所以半径最大的圆的标准方程为.
同课章节目录
