勾股定理
图片预览


文档简介
(共21张PPT)
雷州市白沙中学
何海兰
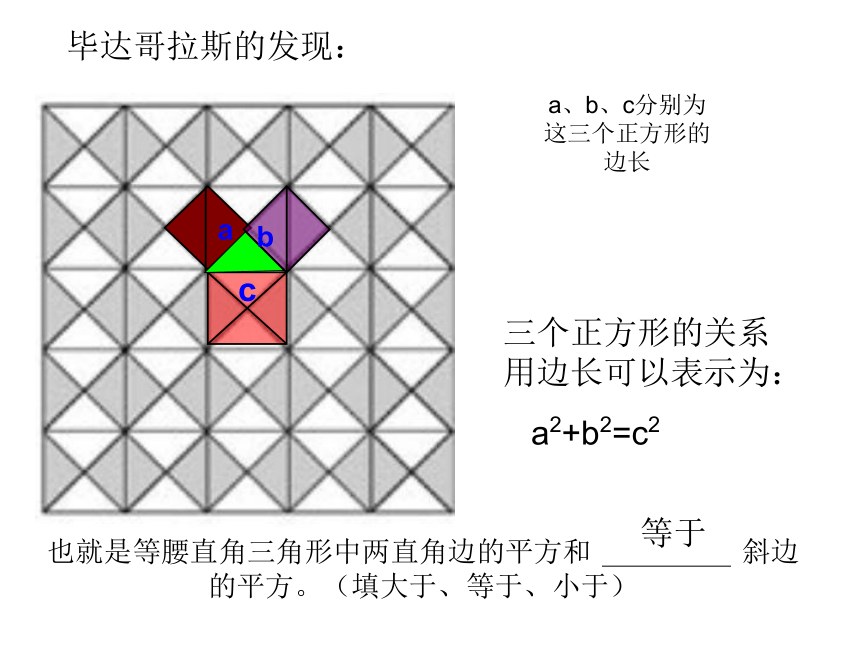
相传2500年前,古希腊著名的数学家毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。
毕达哥拉斯的发现:
三个正方形的关系用边长可以表示为:
a2+b2=c2
a
b
c
也就是等腰直角三角形中两直角边的平方和 斜边的平方。(填大于、等于、小于)
等于
a、b、c分别为这三个正方形的边长
P
O
Q
图1
P
O
Q
图2
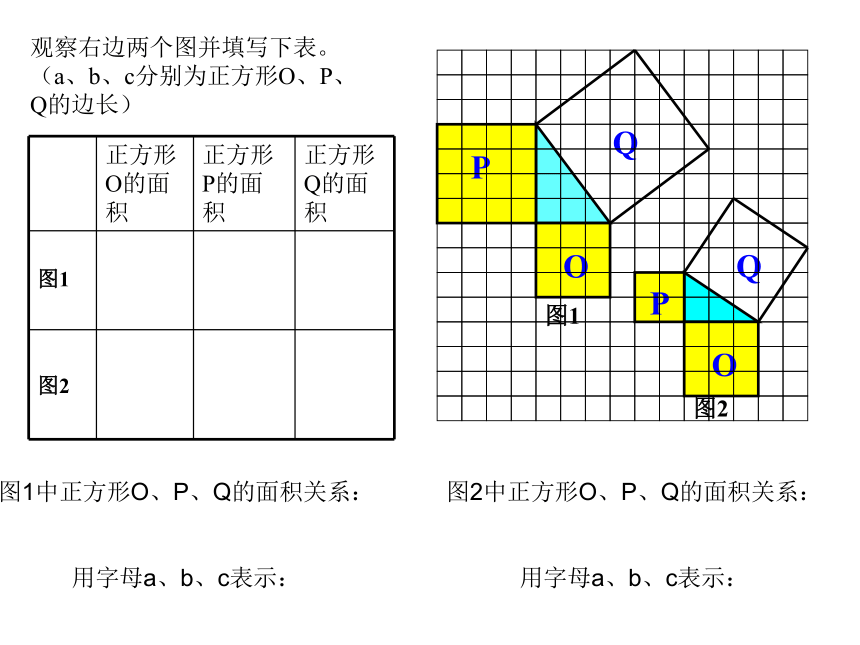
观察右边两个图并填写下表。(a、b、c分别为正方形O、P、Q的边长)
正方形O的面积 正方形P的面积 正方形Q的面积
图1
图2
图1中正方形O、P、Q的面积关系:
用字母a、b、c表示:
图2中正方形O、P、Q的面积关系:
用字母a、b、c表示:
P
O
Q
图1
P
O
Q
图2
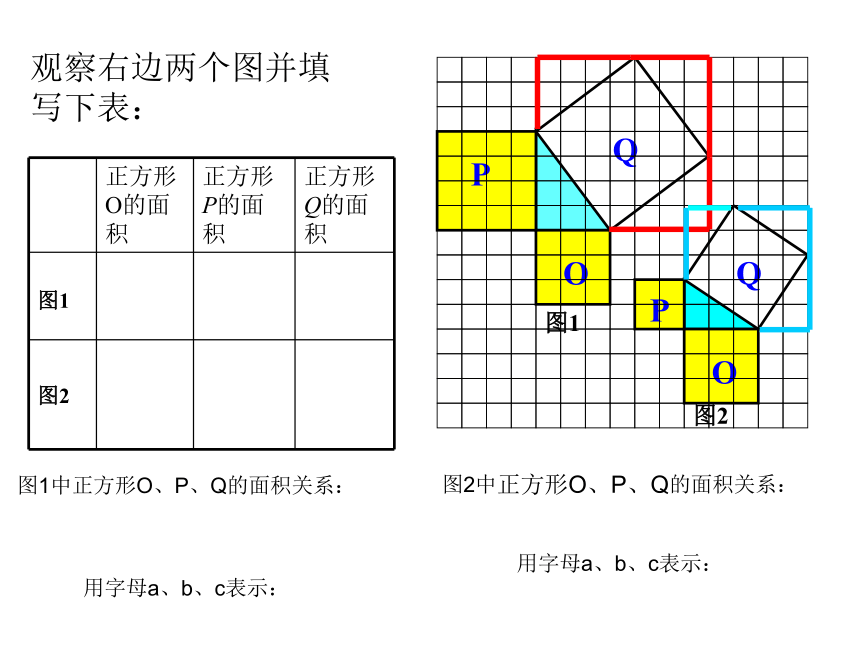
观察右边两个图并填写下表:
正方形O的面积 正方形P的面积 正方形Q的面积
图1
图2
图1中正方形O、P、Q的面积关系:
用字母a、b、c表示:
图2中正方形O、P、Q的面积关系:
用字母a、b、c表示:
P
O
Q
图1
P
O
Q
图2
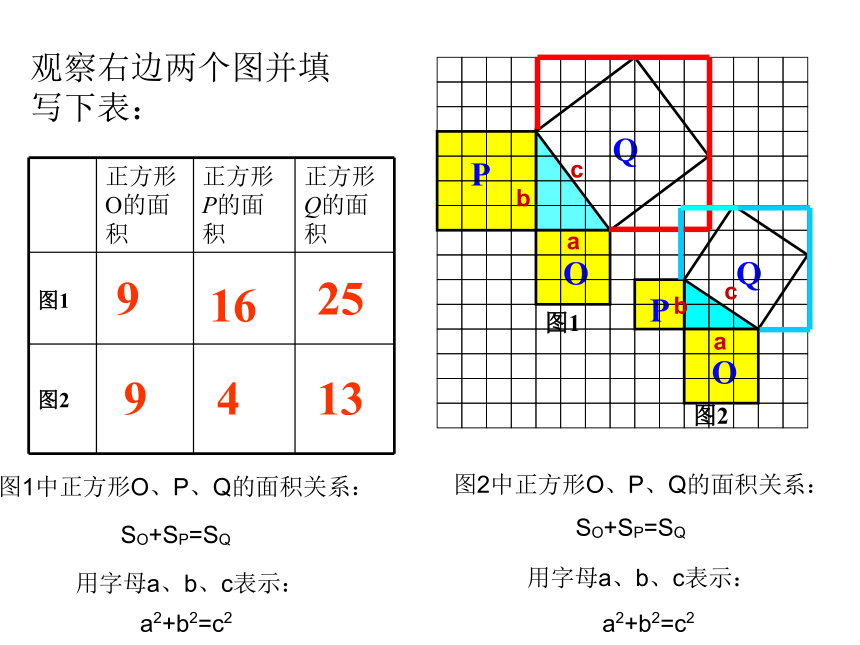
观察右边两个图并填写下表:
正方形O的面积 正方形P的面积 正方形Q的面积
图1
图2
16
9
25
4
9
13
a
b
c
b
a
c
图1中正方形O、P、Q的面积关系:
用字母a、b、c表示:
用字母a、b、c表示:
图2中正方形O、P、Q的面积关系:
SO+SP=SQ
a2+b2=c2
SO+SP=SQ
a2+b2=c2
┏
a
c
b
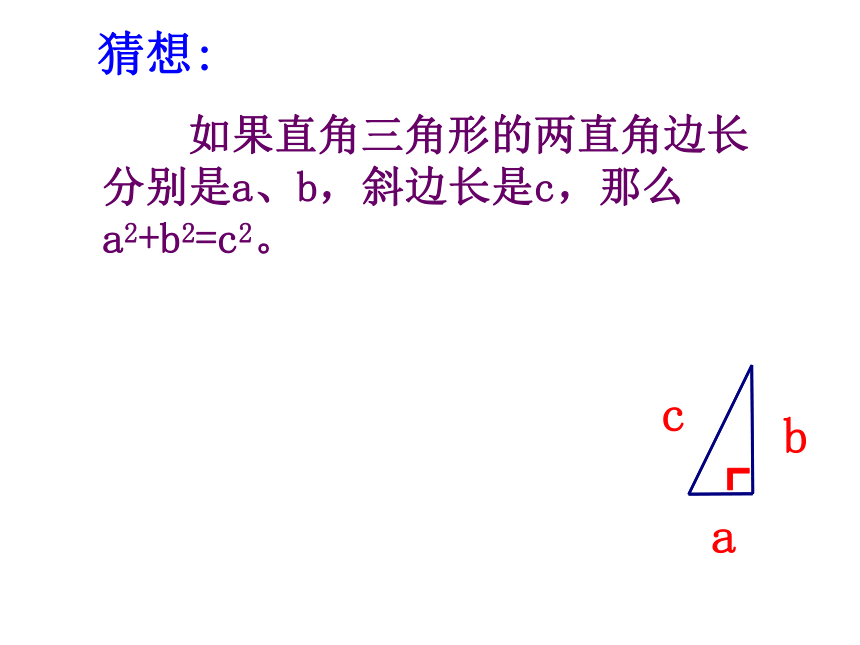
如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。
猜想:
可得:
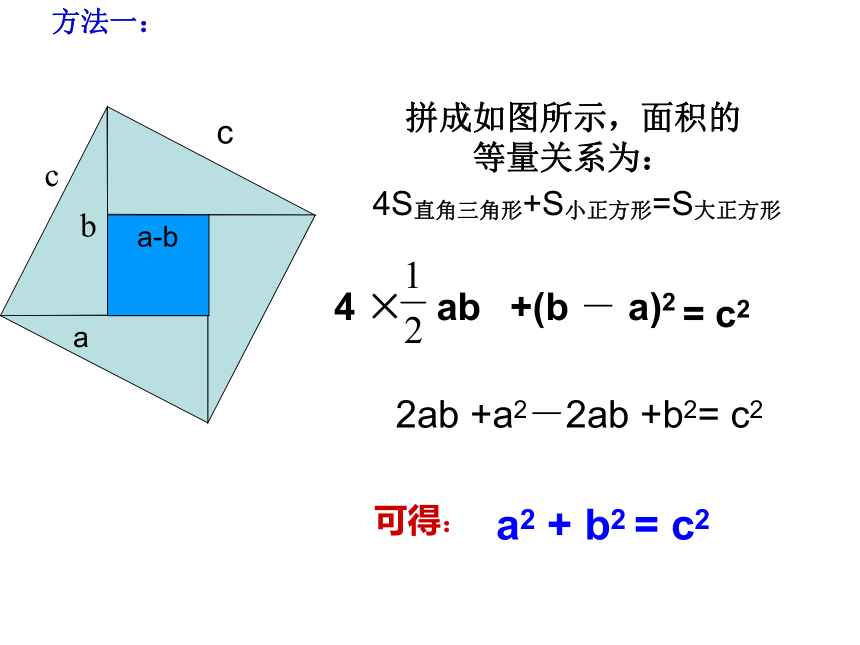
2ab +a2-2ab +b2= c2
b
c
方法一:
c
a
a2 + b2 = c2
4S直角三角形+S小正方形=S大正方形
拼成如图所示,面积的等量关系为:
+(b - a)2
4 ×
ab
= c2
a-b
a
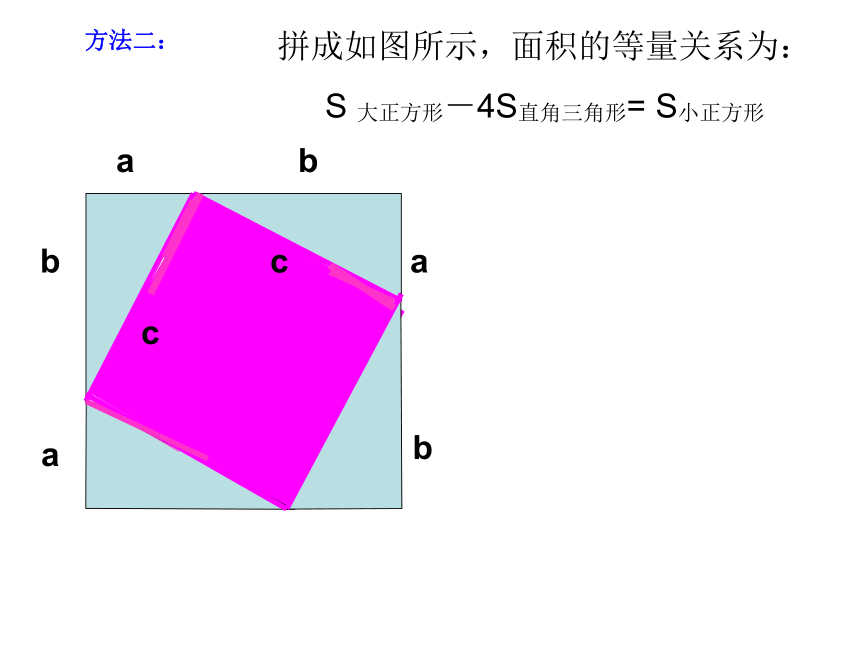
方法二:
b
a
b
b
拼成如图所示,面积的等量关系为:
S 大正方形-4S直角三角形= S小正方形
c
c
a
勾股定理
a
b
c
直角三角形两直角边的平方和等于斜边的平方。
a2+b2=c2
注意:
(1)勾股定理是研究直角三角形三边 关系的定理。如果一个直角三角形知道任意两边的长,就可以求出第三边的长。
(2)勾股定理的变形公式:
c2=a2+b2 a2=c2-b2 b2=c2-a2
1、我国古代的数学家把直角三角形短的直角边叫做“勾”,长的直角边叫做“股”,斜边叫做“弦”。当 “勾”等于3,“股”等于4时,“弦”就必定等于5,也就是勾3、股4、弦5,并且满足勾2+股2=弦2。我国称这个定理为勾股定理,又叫商高定理。
2、勾股定理在外国称为毕达哥拉斯定理、百牛定理。相传是古希腊数学家毕达哥拉斯发现的。比我国的发现时间要晚几百年。
勾股定理的由来
例1、 在△ABC中,∠C=900。
(1)若a=5,b=12,则c=
(2)若a=6,c=10,则b=
(3)若b=24,c=25,则a=
c
b
a
B
C
A
定理应用
13
8
7
例 2、在Rt△ABC中,若a=5,b=12,求出c边的长。
a
b
c
A
B
C
c
a
b
A
C
B
情况一:
情况二:
解:在Rt△ABC中,若c为斜边,根据勾股定理得: a2+b2=c2
所以:c=13
若b为斜边,根据勾股定理得:
c2=b2-a2
所以:c=
1、比一比:谁能最快算出下列的x、y的值
8
y
17
12
x
y = 15
x = 13
z = 12
17
8
x
13
12
y
X=
Y=
15
5
2、在平面直角坐标系中,已知点P的坐标为
(6,8),则OP的长是( )
A、9 B、8 C、14 D、10
x
y
O
P(6,8)
D
3、如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步(假设2步是1m)路却踩伤了花草。
4
4、已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C. D.5或
D
课堂小结
这一节课我们学习了哪些知识?你掌握了哪些?
总结:1、勾股定理的内容。
2、证明勾股定理的方法。
3、利用勾股定理,在直角三角形中已知其中两边的长,我们可以求出第三边的长。
1、完成课本习题1、2、3题。
2、课后探索、查询有关勾股定理的证明方法。
雷州市白沙中学
何海兰
相传2500年前,古希腊著名的数学家毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。
毕达哥拉斯的发现:
三个正方形的关系用边长可以表示为:
a2+b2=c2
a
b
c
也就是等腰直角三角形中两直角边的平方和 斜边的平方。(填大于、等于、小于)
等于
a、b、c分别为这三个正方形的边长
P
O
Q
图1
P
O
Q
图2
观察右边两个图并填写下表。(a、b、c分别为正方形O、P、Q的边长)
正方形O的面积 正方形P的面积 正方形Q的面积
图1
图2
图1中正方形O、P、Q的面积关系:
用字母a、b、c表示:
图2中正方形O、P、Q的面积关系:
用字母a、b、c表示:
P
O
Q
图1
P
O
Q
图2
观察右边两个图并填写下表:
正方形O的面积 正方形P的面积 正方形Q的面积
图1
图2
图1中正方形O、P、Q的面积关系:
用字母a、b、c表示:
图2中正方形O、P、Q的面积关系:
用字母a、b、c表示:
P
O
Q
图1
P
O
Q
图2
观察右边两个图并填写下表:
正方形O的面积 正方形P的面积 正方形Q的面积
图1
图2
16
9
25
4
9
13
a
b
c
b
a
c
图1中正方形O、P、Q的面积关系:
用字母a、b、c表示:
用字母a、b、c表示:
图2中正方形O、P、Q的面积关系:
SO+SP=SQ
a2+b2=c2
SO+SP=SQ
a2+b2=c2
┏
a
c
b
如果直角三角形的两直角边长分别是a、b,斜边长是c,那么a2+b2=c2。
猜想:
可得:
2ab +a2-2ab +b2= c2
b
c
方法一:
c
a
a2 + b2 = c2
4S直角三角形+S小正方形=S大正方形
拼成如图所示,面积的等量关系为:
+(b - a)2
4 ×
ab
= c2
a-b
a
方法二:
b
a
b
b
拼成如图所示,面积的等量关系为:
S 大正方形-4S直角三角形= S小正方形
c
c
a
勾股定理
a
b
c
直角三角形两直角边的平方和等于斜边的平方。
a2+b2=c2
注意:
(1)勾股定理是研究直角三角形三边 关系的定理。如果一个直角三角形知道任意两边的长,就可以求出第三边的长。
(2)勾股定理的变形公式:
c2=a2+b2 a2=c2-b2 b2=c2-a2
1、我国古代的数学家把直角三角形短的直角边叫做“勾”,长的直角边叫做“股”,斜边叫做“弦”。当 “勾”等于3,“股”等于4时,“弦”就必定等于5,也就是勾3、股4、弦5,并且满足勾2+股2=弦2。我国称这个定理为勾股定理,又叫商高定理。
2、勾股定理在外国称为毕达哥拉斯定理、百牛定理。相传是古希腊数学家毕达哥拉斯发现的。比我国的发现时间要晚几百年。
勾股定理的由来
例1、 在△ABC中,∠C=900。
(1)若a=5,b=12,则c=
(2)若a=6,c=10,则b=
(3)若b=24,c=25,则a=
c
b
a
B
C
A
定理应用
13
8
7
例 2、在Rt△ABC中,若a=5,b=12,求出c边的长。
a
b
c
A
B
C
c
a
b
A
C
B
情况一:
情况二:
解:在Rt△ABC中,若c为斜边,根据勾股定理得: a2+b2=c2
所以:c=13
若b为斜边,根据勾股定理得:
c2=b2-a2
所以:c=
1、比一比:谁能最快算出下列的x、y的值
8
y
17
12
x
y = 15
x = 13
z = 12
17
8
x
13
12
y
X=
Y=
15
5
2、在平面直角坐标系中,已知点P的坐标为
(6,8),则OP的长是( )
A、9 B、8 C、14 D、10
x
y
O
P(6,8)
D
3、如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步(假设2步是1m)路却踩伤了花草。
4
4、已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C. D.5或
D
课堂小结
这一节课我们学习了哪些知识?你掌握了哪些?
总结:1、勾股定理的内容。
2、证明勾股定理的方法。
3、利用勾股定理,在直角三角形中已知其中两边的长,我们可以求出第三边的长。
1、完成课本习题1、2、3题。
2、课后探索、查询有关勾股定理的证明方法。
