13.2画轴对称图形 过关训练2021-2022学年八年级数学人教版上册(Word版 含答案)
文档属性
| 名称 | 13.2画轴对称图形 过关训练2021-2022学年八年级数学人教版上册(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 863.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 14:54:12 | ||
图片预览



文档简介
2021人教版八年级上轴对称13.2过关训练
一、 选择题
?1. 点(2,??3)关于y轴对称的点的坐标是( )
A.(?2,?3) B.(?2,??3) C.(2,?3) D.(2,??3)
?2. 平面内点A(?1,?2)和点B(?1,?6)的对称轴是( )
A.x轴 B.y轴 C.直线y=4 D.直线x=?1
?3. 若点A(1,?2),B(?1,?2),则点A与点B的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于直线x=1对称 D.关于直线y=1对称
4. 在平面直角坐标系中,点A2,a与点Bb,3关于y轴对称,则(? ? ? ? )
A.a=3,b=?2 B.a=?3,b=2 C.a=2,b=3 D.a=?3,b=?2
?5. 在平面直角坐标系中,点A(m,?2)与点B(3,?n)关于x轴对称,则(m,?n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
?6. 作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
?7. 用刻度尺分别画下列图形的对称轴,可以不用刻度尺上的刻度画的是( )
A.①②③④ B.②③ C.③④ D.①②
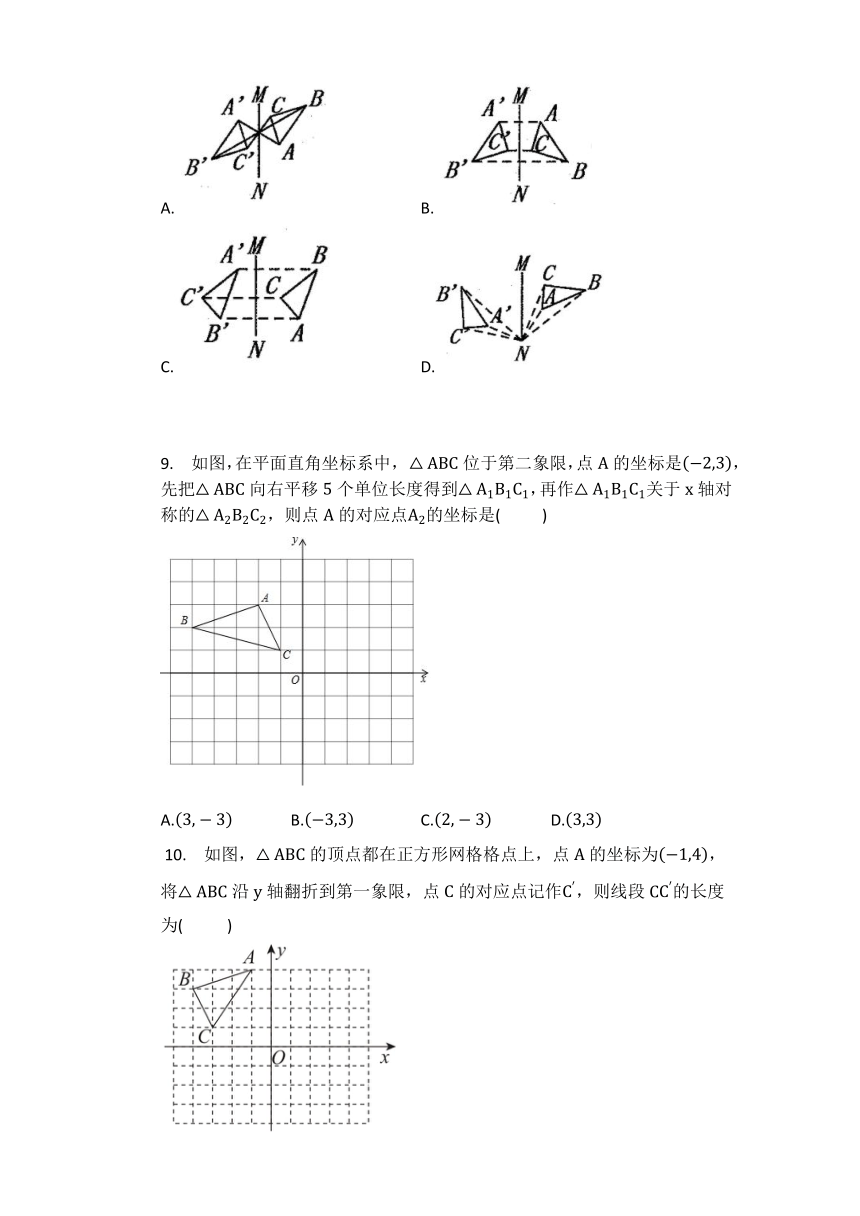
?8. 下列图形中, △A′B′C′ 与△ABC关于直线MN成轴对称的是(????????)
A. B.
C. D.
?
9. 如图,在平面直角坐标系中, △ABC位于第二象限,点A的坐标是?2,3,先把△ABC向右平移5个单位长度得到△A1B1C1,再作△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是(? ? ? ?)
A.3,?3 B.?3,3 C.2,?3 D.3,3
?10. 如图,△ABC的顶点都在正方形网格格点上,点A的坐标为?1,4,将△ABC沿y轴翻折到第一象限,点C的对应点记作C′,则线段CC′的长度为(????????? )
A.2 B.6 C.8 D.9
?11. 坐标平面内,点A和B关于x轴对称,若点A到x轴的距离是3cm,则点B到x轴的距离是( )cm.
A.6 B.3 C.2.5 D.4
?12. 如果点P(?m,?3)与点P1(?5,?n)关于y轴对称,则m,n的值分别为( )
A.m=?5,n=3 B.m=5,n=3 C.m=?5,n=?3 D.m=?3,n=5
?13. 已知点P1(a?1,?5)和P2(2,?b?1)关于x轴对称,则(a+b)2009的值为( )
A.(?3)2009 B.?1 C.0 D.1
?14. 在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(?2,3),先把△ABC右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是(? ? ? ? )
A.(?3,2) B.(2,?3) C.(1,?2) D.(?1,2)
二、 填空题
?15. 已知点A(3,?n)关于y轴对称的点的坐标为(?3,?2),那么n的值为________.
?16. 如果点A(2m?n,?5+m)和点B(2n?1,??m+n)关于y轴对称,则m=________,n=________.
?17. 点M(?3,?2)关于直线x=?1对称的点N的坐标是________,直线MN与x轴的位置关系是________.
18. 已知点A(6a+1,?5)与点B(4?a,?b)关于y轴对称,则aba+b=________.
?19. 如图,△ABC关于α轴对称,点B的坐标是2,?3,则点C的坐标是________.
三、 解答题 ?
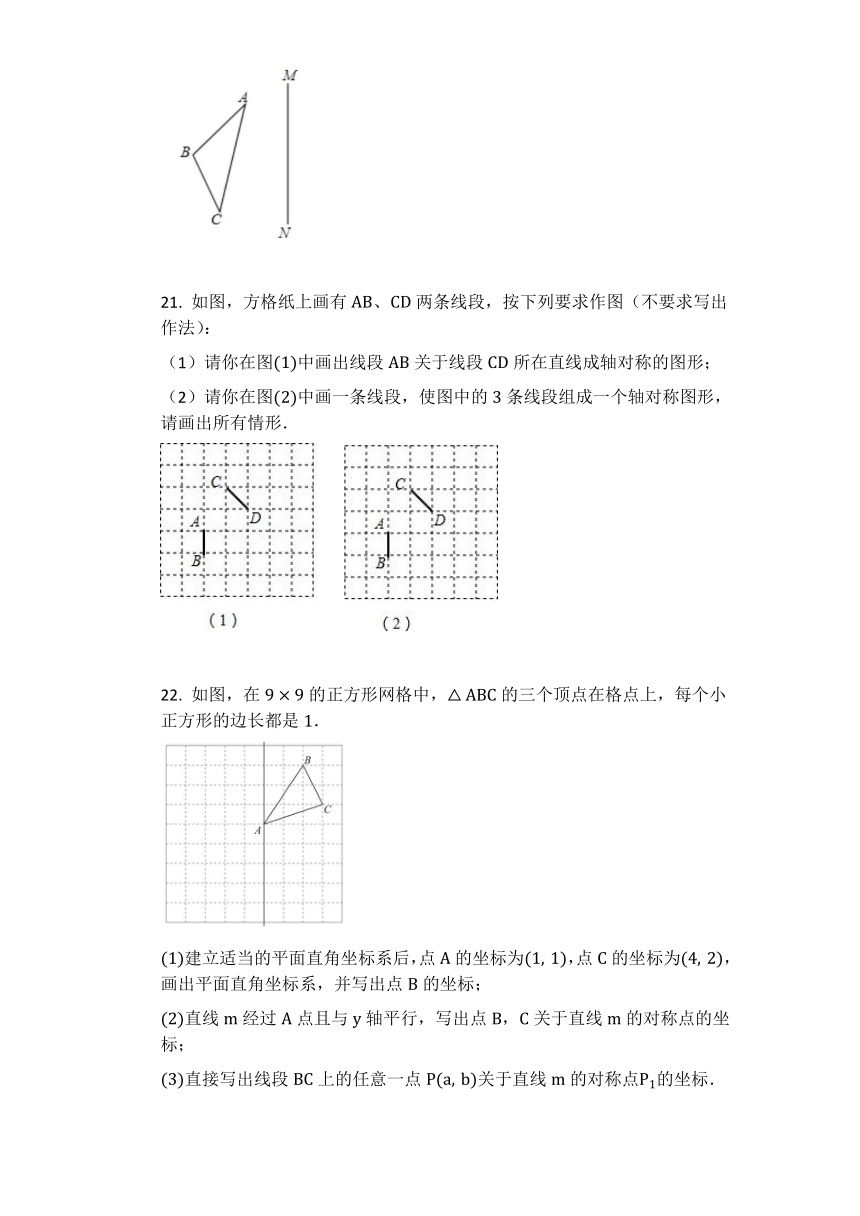
20. 如图:△ABC和直线MN,求作△A1B1C1,使它与△ABC关于直线MN对称(不写作法).
?
21. 如图,方格纸上画有AB、CD两条线段,按下列要求作图(不要求写出作法):
(1)请你在图(1)中画出线段AB关于线段CD所在直线成轴对称的图形;
(2)请你在图(2)中画一条线段,使图中的3条线段组成一个轴对称图形,请画出所有情形.
?
22. 如图,在9×9的正方形网格中,△ABC的三个顶点在格点上,每个小正方形的边长都是1.
(1)建立适当的平面直角坐标系后,点A的坐标为(1,?1),点C的坐标为(4,?2),画出平面直角坐标系,并写出点B的坐标;
(2)直线m经过A点且与y轴平行,写出点B,C关于直线m的对称点的坐标;
(3)直接写出线段BC上的任意一点P(a,?b)关于直线m的对称点P1的坐标.
?
23. 如图是由边长为1的小正方形组成的12×12网格,格点△ABC(顶点是网格线的交点的三角形)的顶点A,B,C的坐标分别为(4,?0),(3,?5),(1,?2).
(1)在如图所示网格中,根据上述点的坐标建立适当的平面直角坐标系,标出原点O;
(2)在(1)建立的平面直角坐标系中,
①画出△ABC关于y轴对称的图形△A1B1C1,点A,B,C的对应点分别为A1,B1,C1,直接写出点B1的坐标;
②若点Px,y是△ABC内部任意一点,直?接?写出点P关于y轴对称的对应点P1的坐标.
?
24. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,?Rt△ABC
顶点均在格点上,在建立平面直角坐标系后,点左的坐标为?(?6,1)
(1)若 Rt△ABC 以γ轴为对称轴的图形为 Rt△A1B1C1 ,试在图上画出 Rt△A1B1C1
若?Rt△A2B2C2?与(1)中的?Rt△A1B1C1?关于x轴为对称轴,试在图上画出
Rt△A2B2C2
(3)试在y轴上找一点P,使?PA+PC?的值最小;
(4)归纳与发现:?Rt△ABC?上的点?Q(m,n)?通过(1)、(2)的两次连续轴对称变换后的对应点?Qn?钓坐标为?Q′
?
25. 图①、图②、图③都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB的端点都在格点上,在图①、图②、图③中,分别以AB为边画一个面积为152的三角形,在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
(1)在图①中画△ABC,使∠BAC=45?.
(2)在图②中画△ABD,使△ABD是轴对称图形.
(3)在图③中画△ABE,使AB边上的高将△ABE分成面积比为1:2的两部分.
参考答案与试题解析
一、 选择题
1.
【答案】
B
【解答】
此题暂无解答
2.
【答案】
C
【解答】
解:∵ 点A(?1,?2)和点B(?1,?6)对称,
且AB平行与y轴,
∴ 对称轴是直线y=12(6+2)=4.
故选C.
3.
【答案】
B
【解答】
∵ 点A(1,?2),B(?1,?2),
∴ 点A与点B关于y轴对称,
4.
【答案】
A
【解答】
解:∵ 点A2,a与点Bb,3关于y轴对称,
∴ a=3,b=?2.
故选A.
5.
【答案】
D
【解答】
∵ 点A(m,?2)与点B(3,?n)关于x轴对称,
∴ m=3,n=?2,
∴ (3,??2)在第四象限.
6.
【答案】
B
【解答】
作已知点关于某直线的对称点的第一步是过已知点作一条直线与已知直线垂直,
7.
【答案】
A
【解答】
①②③④均可以不用刻度尺上的刻度画对称轴.
8.
【答案】
B
【解答】
解:根据轴对称的性质,结合四个选项,
只有B选项中对应点的连线被对称轴MN垂直平分,
所以B是符合要求的.
故选B.
9.
【答案】
A
【解答】
解:如图所示:点A的对应点A2的坐标是:3,?3.
故选A.
10.
【答案】
B
【解答】
解:如图:
∵点A的坐标为(?1,4),
∴ 点C的坐标为(?3,1),
∵ 将△ABC沿y轴翻折到第一象限,
∴ 点C的对应点C′的坐标是(3,1),
∴CC′=3?(?3)=6.
故选B.
11.
【答案】
B
【解答】
解:∵ 点A和B关于x轴对称,
∴ A、B两点到x轴的距离相等,
∵ 若点A到x轴的距离是3cm,
∴ 点B到x轴的距离是3cm,
故选:B.
12.
【答案】
A
【解答】
解:点P和点P1关于y轴对称,
根据题意,有n=3,?m=5;
即m=?5,n=3;
故选A.
13.
【答案】
B
【解答】
解:∵ 点P1(a?1,?5)和P2(2,?b?1)关于x轴对称,
∴ a?1=2,b?1=?5,
解得:a=3,b=?4,
∴ (a+b)2009=?1.
故选:B.
14.
【答案】
B
【解答】
解:如图所示:点A的对应点A2的坐标是:(2,?3).
故选B.
二、 填空题
15.
【答案】
2
【解答】
解:∵ 点A(3,?n)关于y轴对称点的坐标为(?3,?2)
根据关于y轴对称的点的坐标的特点,
∴ n=2.
故答案为2.
16.
【答案】
m=,n=3(答对一个给2分)
【解答】
此题暂无解答
17.
【答案】
(1,?2),平行
【解答】
解:∵ 点M(?3,?2)与点N关于直线x=?1对称,
而?1×2?(?3)=1,
∴ 点M(?3,?2)关于直线x=?1对称的点N的坐标是(1,?2),
∵ 点M与点N的纵坐标相同,
∴ 直线MN与x轴的位置关系是平行.
18.
【答案】
?54
【解答】
解:由点A(6a+1,?5)与点B(4?a,?b)关于y轴对称,得
6a+1+4?a=0,b=5.
解得a=?1,b=5.
则aba+b=?54,
故答案为:?54.
19.
【答案】
(2,3)
【解答】
解:
已知点B的坐标为(2,?3),并且△ABC关于x轴对称,
∴ 点B和C的横坐标不变,纵坐标为相反数.
∴ 点C的坐标为(2,3).
故答案为:(2,3).
三、 解答题
20.
【答案】
解:如图所示:
.
【解答】
解:如图所示:
.
21.
【答案】
解:(1)如图(1)所示:
(2)如图(2)所示.
【解答】
解:(1)如图(1)所示:
(2)如图(2)所示.
22.
【答案】
解:(1)由题意建立平面直角坐标系如图所示,B(3,?4).
(2)由(1)中图可知,
点B关于直线m的对称点的坐标为B′(?1,?4);
点C关于直线m的对称点的坐标为C′(?2,?2).
(3)点P(a,?b)关于直线m的对称点P1的坐标为P1(2?a,?b).
【解答】
解:(1)由题意建立平面直角坐标系如图所示,B(3,?4).
(2)由(1)中图可知,
点B关于直线m的对称点的坐标为B′(?1,?4);
点C关于直线m的对称点的坐标为C′(?2,?2).
(3)点P(a,?b)关于直线m的对称点P1的坐标为P1(2?a,?b).
23.
【答案】
解:建立如图所示的平面直角坐标系;
解:①如图所示△A1B1C1为所求,点B关于y轴对称的点B1的坐标为?3,5;
②点Px,y关于y轴对称的点横坐标是相反数,纵坐标不变,
∴ P1?x,y.
【解答】
此题暂无解答
24.
【答案】
解:(1)如图所示,△A1B1C1就是所要求画的.
(2)如图所示,△A2B2C2就是所要求画的.
(3)如图所示,点P就是所要求画的点.
(4)Q′(?m,?n)
【解答】
解:(1)如图所示,△A1B1C1就是所要求画的.
(2)如图所示,△A2B2C2就是所要求画的.
(3)如图所示,点P就是所要求画的点.
(4)点Q(m,n)关于y轴对称点Q1(?m,n),Q1(?m,n)关于x轴对称点Q′(?m,?n),
∴???Rt△ABC?上的点?Q(m,n)?通过(1)、(2)的两次连续轴对称变换后的对应点??Q′(?m,?n).
故答案为Q′(?m,?n).
25.
【答案】
如图①中,△ABC即为所求.
如图②中,△ABD即为所求(答案不唯一).
如图③中,△ABE即为所求(答案不唯一).
【解答】
如图①中,△ABC即为所求.
如图②中,△ABD即为所求(答案不唯一).
如图③中,△ABE即为所求(答案不唯一).
一、 选择题
?1. 点(2,??3)关于y轴对称的点的坐标是( )
A.(?2,?3) B.(?2,??3) C.(2,?3) D.(2,??3)
?2. 平面内点A(?1,?2)和点B(?1,?6)的对称轴是( )
A.x轴 B.y轴 C.直线y=4 D.直线x=?1
?3. 若点A(1,?2),B(?1,?2),则点A与点B的关系是( )
A.关于x轴对称 B.关于y轴对称
C.关于直线x=1对称 D.关于直线y=1对称
4. 在平面直角坐标系中,点A2,a与点Bb,3关于y轴对称,则(? ? ? ? )
A.a=3,b=?2 B.a=?3,b=2 C.a=2,b=3 D.a=?3,b=?2
?5. 在平面直角坐标系中,点A(m,?2)与点B(3,?n)关于x轴对称,则(m,?n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
?6. 作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
?7. 用刻度尺分别画下列图形的对称轴,可以不用刻度尺上的刻度画的是( )
A.①②③④ B.②③ C.③④ D.①②
?8. 下列图形中, △A′B′C′ 与△ABC关于直线MN成轴对称的是(????????)
A. B.
C. D.
?
9. 如图,在平面直角坐标系中, △ABC位于第二象限,点A的坐标是?2,3,先把△ABC向右平移5个单位长度得到△A1B1C1,再作△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是(? ? ? ?)
A.3,?3 B.?3,3 C.2,?3 D.3,3
?10. 如图,△ABC的顶点都在正方形网格格点上,点A的坐标为?1,4,将△ABC沿y轴翻折到第一象限,点C的对应点记作C′,则线段CC′的长度为(????????? )
A.2 B.6 C.8 D.9
?11. 坐标平面内,点A和B关于x轴对称,若点A到x轴的距离是3cm,则点B到x轴的距离是( )cm.
A.6 B.3 C.2.5 D.4
?12. 如果点P(?m,?3)与点P1(?5,?n)关于y轴对称,则m,n的值分别为( )
A.m=?5,n=3 B.m=5,n=3 C.m=?5,n=?3 D.m=?3,n=5
?13. 已知点P1(a?1,?5)和P2(2,?b?1)关于x轴对称,则(a+b)2009的值为( )
A.(?3)2009 B.?1 C.0 D.1
?14. 在平面直角坐标系中,△ABC位于第二象限,点A的坐标是(?2,3),先把△ABC右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x轴对称的△A2B2C2,则点A的对应点A2的坐标是(? ? ? ? )
A.(?3,2) B.(2,?3) C.(1,?2) D.(?1,2)
二、 填空题
?15. 已知点A(3,?n)关于y轴对称的点的坐标为(?3,?2),那么n的值为________.
?16. 如果点A(2m?n,?5+m)和点B(2n?1,??m+n)关于y轴对称,则m=________,n=________.
?17. 点M(?3,?2)关于直线x=?1对称的点N的坐标是________,直线MN与x轴的位置关系是________.
18. 已知点A(6a+1,?5)与点B(4?a,?b)关于y轴对称,则aba+b=________.
?19. 如图,△ABC关于α轴对称,点B的坐标是2,?3,则点C的坐标是________.
三、 解答题 ?
20. 如图:△ABC和直线MN,求作△A1B1C1,使它与△ABC关于直线MN对称(不写作法).
?
21. 如图,方格纸上画有AB、CD两条线段,按下列要求作图(不要求写出作法):
(1)请你在图(1)中画出线段AB关于线段CD所在直线成轴对称的图形;
(2)请你在图(2)中画一条线段,使图中的3条线段组成一个轴对称图形,请画出所有情形.
?
22. 如图,在9×9的正方形网格中,△ABC的三个顶点在格点上,每个小正方形的边长都是1.
(1)建立适当的平面直角坐标系后,点A的坐标为(1,?1),点C的坐标为(4,?2),画出平面直角坐标系,并写出点B的坐标;
(2)直线m经过A点且与y轴平行,写出点B,C关于直线m的对称点的坐标;
(3)直接写出线段BC上的任意一点P(a,?b)关于直线m的对称点P1的坐标.
?
23. 如图是由边长为1的小正方形组成的12×12网格,格点△ABC(顶点是网格线的交点的三角形)的顶点A,B,C的坐标分别为(4,?0),(3,?5),(1,?2).
(1)在如图所示网格中,根据上述点的坐标建立适当的平面直角坐标系,标出原点O;
(2)在(1)建立的平面直角坐标系中,
①画出△ABC关于y轴对称的图形△A1B1C1,点A,B,C的对应点分别为A1,B1,C1,直接写出点B1的坐标;
②若点Px,y是△ABC内部任意一点,直?接?写出点P关于y轴对称的对应点P1的坐标.
?
24. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,?Rt△ABC
顶点均在格点上,在建立平面直角坐标系后,点左的坐标为?(?6,1)
(1)若 Rt△ABC 以γ轴为对称轴的图形为 Rt△A1B1C1 ,试在图上画出 Rt△A1B1C1
若?Rt△A2B2C2?与(1)中的?Rt△A1B1C1?关于x轴为对称轴,试在图上画出
Rt△A2B2C2
(3)试在y轴上找一点P,使?PA+PC?的值最小;
(4)归纳与发现:?Rt△ABC?上的点?Q(m,n)?通过(1)、(2)的两次连续轴对称变换后的对应点?Qn?钓坐标为?Q′
?
25. 图①、图②、图③都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB的端点都在格点上,在图①、图②、图③中,分别以AB为边画一个面积为152的三角形,在给定的网格中,只用无刻度的直尺,按下列要求画图,只保留作图痕迹,不要求写画法.
(1)在图①中画△ABC,使∠BAC=45?.
(2)在图②中画△ABD,使△ABD是轴对称图形.
(3)在图③中画△ABE,使AB边上的高将△ABE分成面积比为1:2的两部分.
参考答案与试题解析
一、 选择题
1.
【答案】
B
【解答】
此题暂无解答
2.
【答案】
C
【解答】
解:∵ 点A(?1,?2)和点B(?1,?6)对称,
且AB平行与y轴,
∴ 对称轴是直线y=12(6+2)=4.
故选C.
3.
【答案】
B
【解答】
∵ 点A(1,?2),B(?1,?2),
∴ 点A与点B关于y轴对称,
4.
【答案】
A
【解答】
解:∵ 点A2,a与点Bb,3关于y轴对称,
∴ a=3,b=?2.
故选A.
5.
【答案】
D
【解答】
∵ 点A(m,?2)与点B(3,?n)关于x轴对称,
∴ m=3,n=?2,
∴ (3,??2)在第四象限.
6.
【答案】
B
【解答】
作已知点关于某直线的对称点的第一步是过已知点作一条直线与已知直线垂直,
7.
【答案】
A
【解答】
①②③④均可以不用刻度尺上的刻度画对称轴.
8.
【答案】
B
【解答】
解:根据轴对称的性质,结合四个选项,
只有B选项中对应点的连线被对称轴MN垂直平分,
所以B是符合要求的.
故选B.
9.
【答案】
A
【解答】
解:如图所示:点A的对应点A2的坐标是:3,?3.
故选A.
10.
【答案】
B
【解答】
解:如图:
∵点A的坐标为(?1,4),
∴ 点C的坐标为(?3,1),
∵ 将△ABC沿y轴翻折到第一象限,
∴ 点C的对应点C′的坐标是(3,1),
∴CC′=3?(?3)=6.
故选B.
11.
【答案】
B
【解答】
解:∵ 点A和B关于x轴对称,
∴ A、B两点到x轴的距离相等,
∵ 若点A到x轴的距离是3cm,
∴ 点B到x轴的距离是3cm,
故选:B.
12.
【答案】
A
【解答】
解:点P和点P1关于y轴对称,
根据题意,有n=3,?m=5;
即m=?5,n=3;
故选A.
13.
【答案】
B
【解答】
解:∵ 点P1(a?1,?5)和P2(2,?b?1)关于x轴对称,
∴ a?1=2,b?1=?5,
解得:a=3,b=?4,
∴ (a+b)2009=?1.
故选:B.
14.
【答案】
B
【解答】
解:如图所示:点A的对应点A2的坐标是:(2,?3).
故选B.
二、 填空题
15.
【答案】
2
【解答】
解:∵ 点A(3,?n)关于y轴对称点的坐标为(?3,?2)
根据关于y轴对称的点的坐标的特点,
∴ n=2.
故答案为2.
16.
【答案】
m=,n=3(答对一个给2分)
【解答】
此题暂无解答
17.
【答案】
(1,?2),平行
【解答】
解:∵ 点M(?3,?2)与点N关于直线x=?1对称,
而?1×2?(?3)=1,
∴ 点M(?3,?2)关于直线x=?1对称的点N的坐标是(1,?2),
∵ 点M与点N的纵坐标相同,
∴ 直线MN与x轴的位置关系是平行.
18.
【答案】
?54
【解答】
解:由点A(6a+1,?5)与点B(4?a,?b)关于y轴对称,得
6a+1+4?a=0,b=5.
解得a=?1,b=5.
则aba+b=?54,
故答案为:?54.
19.
【答案】
(2,3)
【解答】
解:
已知点B的坐标为(2,?3),并且△ABC关于x轴对称,
∴ 点B和C的横坐标不变,纵坐标为相反数.
∴ 点C的坐标为(2,3).
故答案为:(2,3).
三、 解答题
20.
【答案】
解:如图所示:
.
【解答】
解:如图所示:
.
21.
【答案】
解:(1)如图(1)所示:
(2)如图(2)所示.
【解答】
解:(1)如图(1)所示:
(2)如图(2)所示.
22.
【答案】
解:(1)由题意建立平面直角坐标系如图所示,B(3,?4).
(2)由(1)中图可知,
点B关于直线m的对称点的坐标为B′(?1,?4);
点C关于直线m的对称点的坐标为C′(?2,?2).
(3)点P(a,?b)关于直线m的对称点P1的坐标为P1(2?a,?b).
【解答】
解:(1)由题意建立平面直角坐标系如图所示,B(3,?4).
(2)由(1)中图可知,
点B关于直线m的对称点的坐标为B′(?1,?4);
点C关于直线m的对称点的坐标为C′(?2,?2).
(3)点P(a,?b)关于直线m的对称点P1的坐标为P1(2?a,?b).
23.
【答案】
解:建立如图所示的平面直角坐标系;
解:①如图所示△A1B1C1为所求,点B关于y轴对称的点B1的坐标为?3,5;
②点Px,y关于y轴对称的点横坐标是相反数,纵坐标不变,
∴ P1?x,y.
【解答】
此题暂无解答
24.
【答案】
解:(1)如图所示,△A1B1C1就是所要求画的.
(2)如图所示,△A2B2C2就是所要求画的.
(3)如图所示,点P就是所要求画的点.
(4)Q′(?m,?n)
【解答】
解:(1)如图所示,△A1B1C1就是所要求画的.
(2)如图所示,△A2B2C2就是所要求画的.
(3)如图所示,点P就是所要求画的点.
(4)点Q(m,n)关于y轴对称点Q1(?m,n),Q1(?m,n)关于x轴对称点Q′(?m,?n),
∴???Rt△ABC?上的点?Q(m,n)?通过(1)、(2)的两次连续轴对称变换后的对应点??Q′(?m,?n).
故答案为Q′(?m,?n).
25.
【答案】
如图①中,△ABC即为所求.
如图②中,△ABD即为所求(答案不唯一).
如图③中,△ABE即为所求(答案不唯一).
【解答】
如图①中,△ABC即为所求.
如图②中,△ABD即为所求(答案不唯一).
如图③中,△ABE即为所求(答案不唯一).
