第一章全等三角形提优单元测试2020-2021学年苏科版八年级上册(word版含答案)
文档属性
| 名称 | 第一章全等三角形提优单元测试2020-2021学年苏科版八年级上册(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览

文档简介
全等三角形单元测试(含答案)
考试时间:90分钟 满分:100分 成绩:_______
一、选择题(每题3分,共24分)
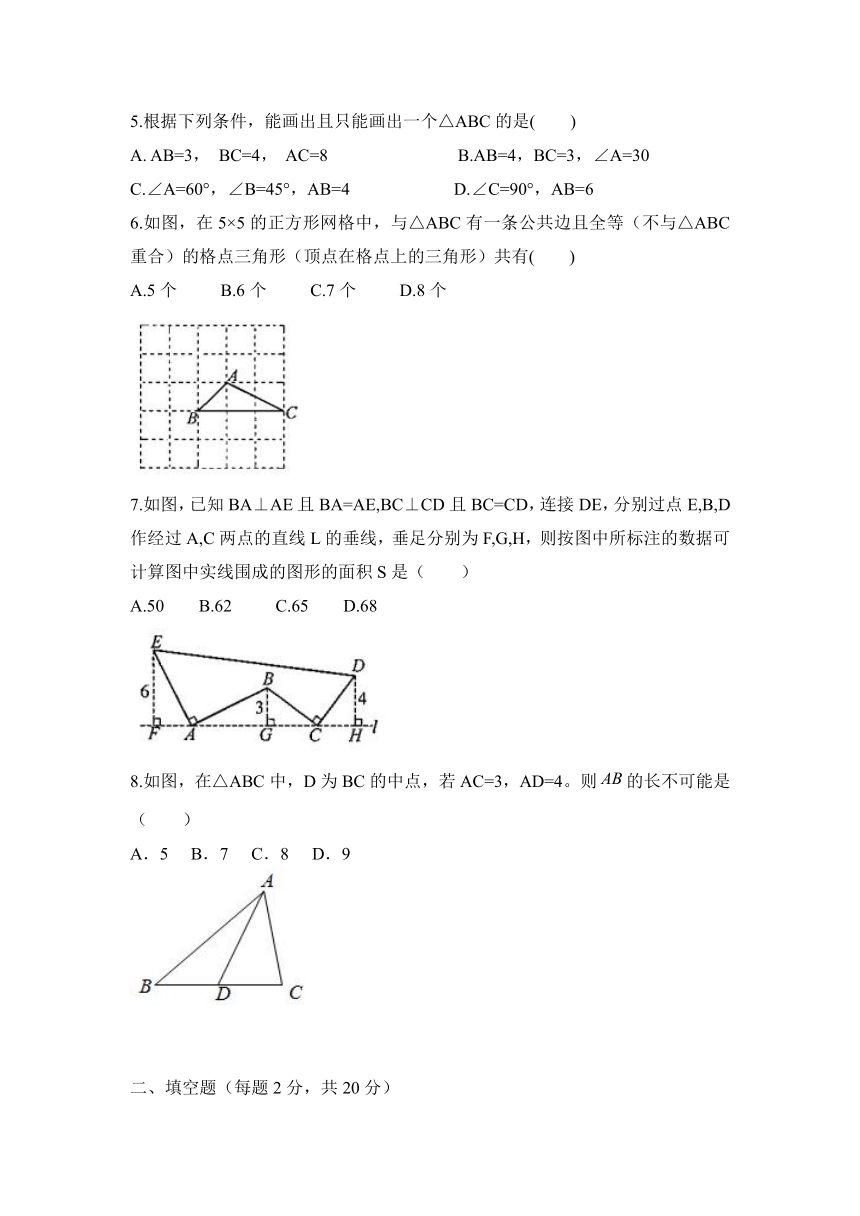
1.已知AB=DC,∠ABC=∠DCB,则能直接判定△ABC≌△DCB的方法是( )
A. SAS B.AAS C.SSS D. ASA
2.如图,已知OA=OB,OC=OD若∠O=50°,∠D=35°,则∠AEC的度数为( )
A.30° B.45° C.50° D.60°
3.如图,D是AB上的一点,DF交AC于点E,DE=FE,FC∥AB若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
4.已知△ABC的三个内角、三条边长如图所示,则甲、乙、丙三个三角形中,和△ABC全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
5.根据下列条件,能画出且只能画出一个△ABC的是( )
A. AB=3, BC=4, AC=8 B.AB=4,BC=3,∠A=30
C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=6
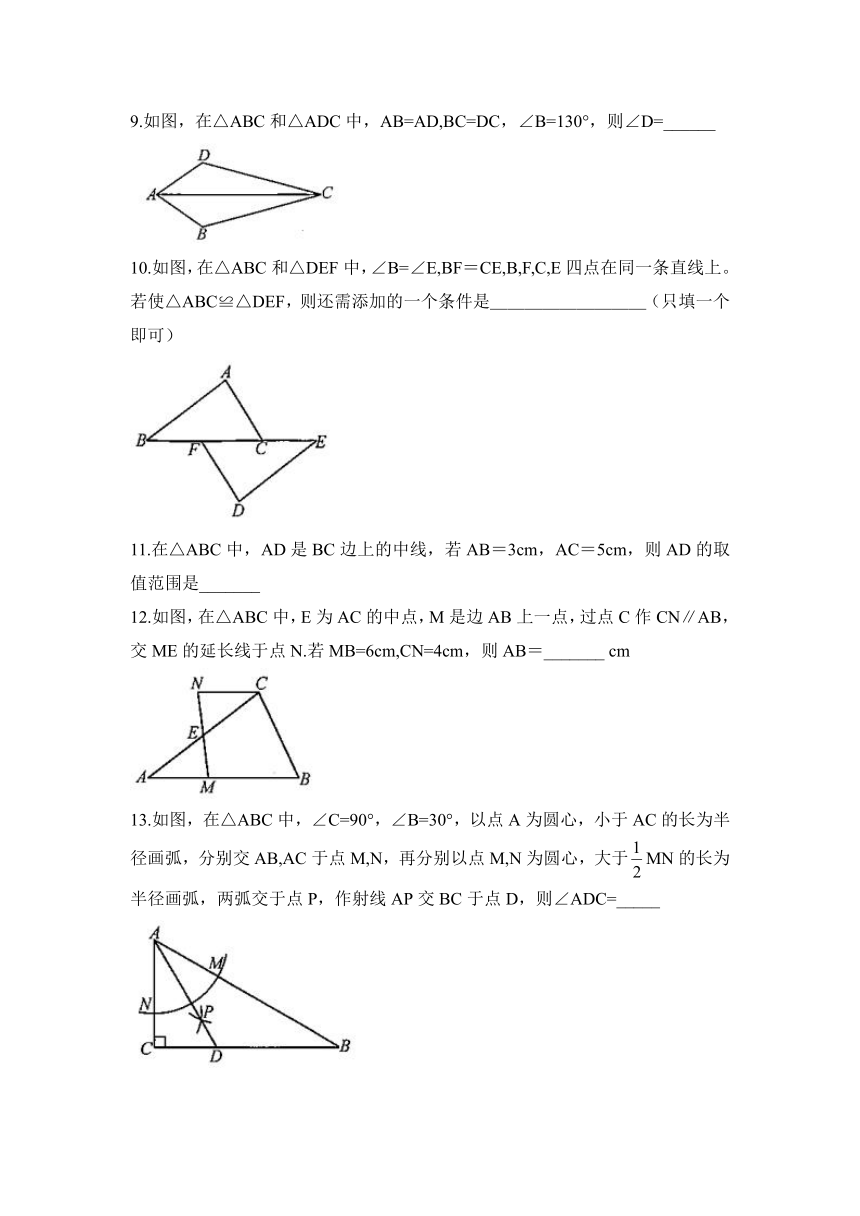
6.如图,在5×5的正方形网格中,与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点在格点上的三角形)共有( )
A.5个 B.6个 C.7个 D.8个
7.如图,已知BA⊥AE且BA=AE,BC⊥CD且BC=CD,连接DE,分别过点E,B,D作经过A,C两点的直线L的垂线,垂足分别为F,G,H,则按图中所标注的数据可计算图中实线围成的图形的面积S是( )
A.50 B.62 C.65 D.68
8.如图,在△ABC中,D为BC的中点,若AC=3,AD=4。则false的长不可能是( )
A.5 B.7 C.8 D.9
二、填空题(每题2分,共20分)
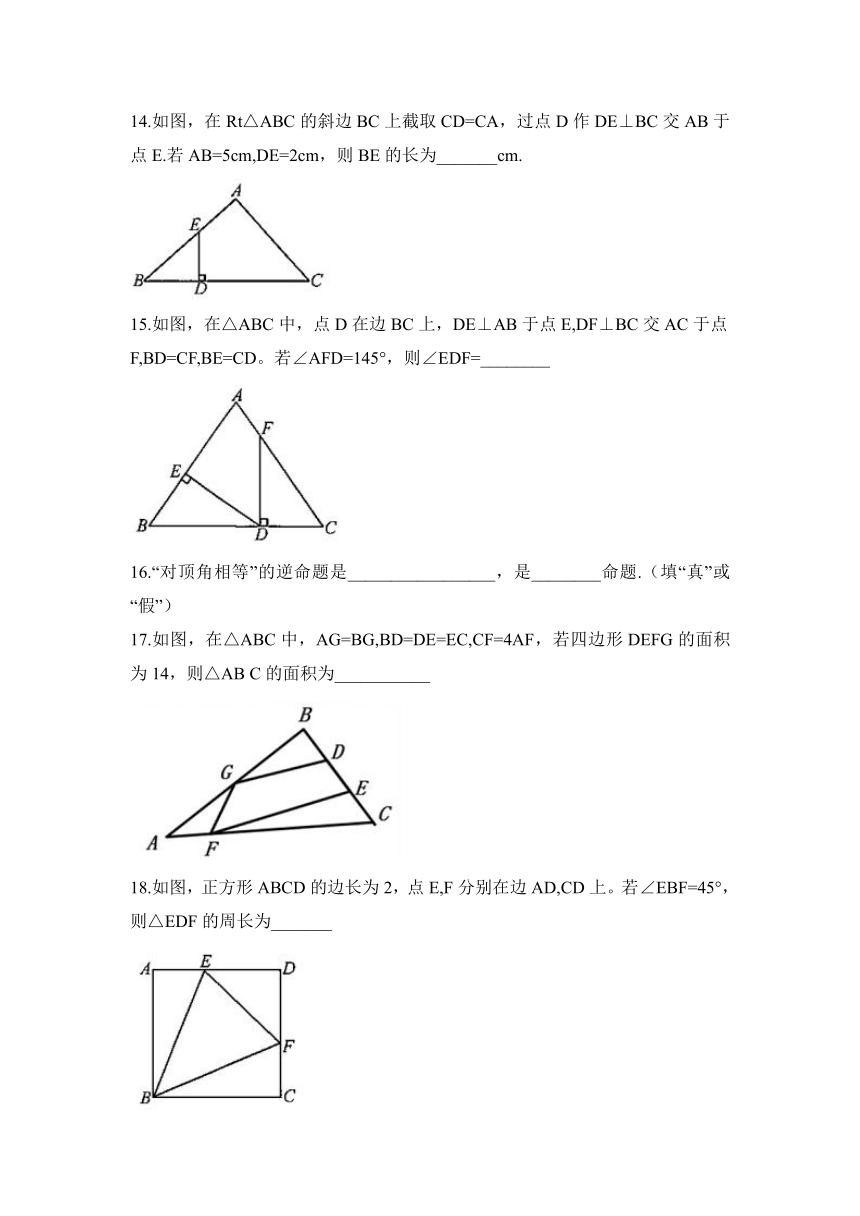
9.如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D=______
10.如图,在△ABC和△DEF中,∠B=∠E,BF=CE,B,F,C,E四点在同一条直线上。若使△ABC≌△DEF,则还需添加的一个条件是_________(只填一个即可)
11.在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是_______
12.如图,在△ABC中,E为AC的中点,M是边AB上一点,过点C作CN∥AB,交ME的延长线于点N.若MB=6cm,CN=4cm,则AB=_______ cm
13.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于falseMN的长为半径画弧,两弧交于点P,作射线AP交BC于点D,则∠ADC=_____
14.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E.若AB=5cm,DE=2cm,则BE的长为_______cm.
15.如图,在△ABC中,点D在边BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD。若∠AFD=145°,则∠EDF=________
16.“对顶角相等”的逆命题是_________________,是________命题.(填“真”或“假”)
17.如图,在△ABC中,AG=BG,BD=DE=EC,CF=4AF,若四边形DEFG的面积为14,则△AB C的面积为___________
18.如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上。若∠EBF=45°,则△EDF的周长为_______
三、解答题(共56分)
19.(6分)如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE。求证:BD=CE.
20.(6分)如图,点A,B,C,D在一条直线上,EA∥FB, EA=FB, AB=CD
(1)求证:∠E=∠F
(2)若∠A=40°,∠D=80°,求∠E的度数
21.(6分)如图,画出一个与△ABC全等的格点三角形(顶点都是小正方形的顶点的三角形称为格点三角形)。在图中共可以画出多少个符合题意的三角形(不包括△ABC)?
22.(6分)如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD
23.(8分)如图,C为直线l上的一点,A,B为直线l外两点,过A,B两点作直线l的垂线,垂足分别为D,E,连接BC,AB,且AB交直线l于点F。若AC=CB,AD=CE,求证:(1)CE=BE+DE (2)AC⊥BC.
24.(8分)如图,△ABC中,AD为中线,E为AB上一点,AD,CE交于点F,且AE=EF。求证:AB=CF
25.(8分)如图,已知△ABC中,点D在AB上,点E在AC的延长线上,且BD=CE,连接DE交BC于点G,若DG=GE,证明:△ABC为等腰三角形.
26.(8分)
(1)如图①,在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,E, F分别是边BC,CD上的点,且∠EAF=∠BAD。求证:EF=BE+DF;
(2)如图②,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?请说明理由;
(3)如图③,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明
参考答案
选择题
1~5 ADBBC 6~8 BAA
填空题
9、130° 10、∠A=∠D(答案不唯一) 11、1<AD<4 12、10
13、60° 14、3 15、55° 16、相等的角是对顶角 假
17、30 18、4
解答题
易证△ABD≌△ACE(ASA),即可得到BD=CE
(1)易证△ACE≌△BDF(SAS),即可得到∠E=∠F
(2)60°
21、图略,23个
22、(截长补短法)在AB上截取AE=AC,易证△CAD≌△EAD,再利用角相等证出CD=BE即可
23、(三垂直模型)(1)易证Rt△ACD≌Rt△CBE(HL),即可得到CE=BE+DE
(2)利用第一问全等得出对应角相等,再利用等量代换得出∠ACB=90°,即可证明
24、(倍长中线法)延长AD到H,使DH=AD,可得△ABD≌△HCD,即可转化AB,再根据条件证△CFH是等腰三角形即可
25、过D作DH∥AC交BC于H,易证△DGH≌△EGC,得出DH=CE,即可得到△BDH是等腰三角形,再利用平行证出△ABC为等腰三角形
26、(半角模型)(1)延长CB到H,使BH=DF,证出△AEH≌△AEF即可
(2)与第一问相同做法和思路
(3)在BC上截取BH=DF,证出△AEH≌△AEF即可证出:BE=EF+DF
考试时间:90分钟 满分:100分 成绩:_______
一、选择题(每题3分,共24分)
1.已知AB=DC,∠ABC=∠DCB,则能直接判定△ABC≌△DCB的方法是( )
A. SAS B.AAS C.SSS D. ASA
2.如图,已知OA=OB,OC=OD若∠O=50°,∠D=35°,则∠AEC的度数为( )
A.30° B.45° C.50° D.60°
3.如图,D是AB上的一点,DF交AC于点E,DE=FE,FC∥AB若AB=4,CF=3,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
4.已知△ABC的三个内角、三条边长如图所示,则甲、乙、丙三个三角形中,和△ABC全等的图形是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
5.根据下列条件,能画出且只能画出一个△ABC的是( )
A. AB=3, BC=4, AC=8 B.AB=4,BC=3,∠A=30
C.∠A=60°,∠B=45°,AB=4 D.∠C=90°,AB=6
6.如图,在5×5的正方形网格中,与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点在格点上的三角形)共有( )
A.5个 B.6个 C.7个 D.8个
7.如图,已知BA⊥AE且BA=AE,BC⊥CD且BC=CD,连接DE,分别过点E,B,D作经过A,C两点的直线L的垂线,垂足分别为F,G,H,则按图中所标注的数据可计算图中实线围成的图形的面积S是( )
A.50 B.62 C.65 D.68
8.如图,在△ABC中,D为BC的中点,若AC=3,AD=4。则false的长不可能是( )
A.5 B.7 C.8 D.9
二、填空题(每题2分,共20分)
9.如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=130°,则∠D=______
10.如图,在△ABC和△DEF中,∠B=∠E,BF=CE,B,F,C,E四点在同一条直线上。若使△ABC≌△DEF,则还需添加的一个条件是_________(只填一个即可)
11.在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是_______
12.如图,在△ABC中,E为AC的中点,M是边AB上一点,过点C作CN∥AB,交ME的延长线于点N.若MB=6cm,CN=4cm,则AB=_______ cm
13.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于falseMN的长为半径画弧,两弧交于点P,作射线AP交BC于点D,则∠ADC=_____
14.如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC交AB于点E.若AB=5cm,DE=2cm,则BE的长为_______cm.
15.如图,在△ABC中,点D在边BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD。若∠AFD=145°,则∠EDF=________
16.“对顶角相等”的逆命题是_________________,是________命题.(填“真”或“假”)
17.如图,在△ABC中,AG=BG,BD=DE=EC,CF=4AF,若四边形DEFG的面积为14,则△AB C的面积为___________
18.如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上。若∠EBF=45°,则△EDF的周长为_______
三、解答题(共56分)
19.(6分)如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE。求证:BD=CE.
20.(6分)如图,点A,B,C,D在一条直线上,EA∥FB, EA=FB, AB=CD
(1)求证:∠E=∠F
(2)若∠A=40°,∠D=80°,求∠E的度数
21.(6分)如图,画出一个与△ABC全等的格点三角形(顶点都是小正方形的顶点的三角形称为格点三角形)。在图中共可以画出多少个符合题意的三角形(不包括△ABC)?
22.(6分)如图,已知在△ABC中,∠C=2∠B,∠1=∠2,求证:AB=AC+CD
23.(8分)如图,C为直线l上的一点,A,B为直线l外两点,过A,B两点作直线l的垂线,垂足分别为D,E,连接BC,AB,且AB交直线l于点F。若AC=CB,AD=CE,求证:(1)CE=BE+DE (2)AC⊥BC.
24.(8分)如图,△ABC中,AD为中线,E为AB上一点,AD,CE交于点F,且AE=EF。求证:AB=CF
25.(8分)如图,已知△ABC中,点D在AB上,点E在AC的延长线上,且BD=CE,连接DE交BC于点G,若DG=GE,证明:△ABC为等腰三角形.
26.(8分)
(1)如图①,在四边形ABCD中,AB=AD,∠ABC=∠ADC=90°,E, F分别是边BC,CD上的点,且∠EAF=∠BAD。求证:EF=BE+DF;
(2)如图②,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?请说明理由;
(3)如图③,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E,F分别是边BC,CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明
参考答案
选择题
1~5 ADBBC 6~8 BAA
填空题
9、130° 10、∠A=∠D(答案不唯一) 11、1<AD<4 12、10
13、60° 14、3 15、55° 16、相等的角是对顶角 假
17、30 18、4
解答题
易证△ABD≌△ACE(ASA),即可得到BD=CE
(1)易证△ACE≌△BDF(SAS),即可得到∠E=∠F
(2)60°
21、图略,23个
22、(截长补短法)在AB上截取AE=AC,易证△CAD≌△EAD,再利用角相等证出CD=BE即可
23、(三垂直模型)(1)易证Rt△ACD≌Rt△CBE(HL),即可得到CE=BE+DE
(2)利用第一问全等得出对应角相等,再利用等量代换得出∠ACB=90°,即可证明
24、(倍长中线法)延长AD到H,使DH=AD,可得△ABD≌△HCD,即可转化AB,再根据条件证△CFH是等腰三角形即可
25、过D作DH∥AC交BC于H,易证△DGH≌△EGC,得出DH=CE,即可得到△BDH是等腰三角形,再利用平行证出△ABC为等腰三角形
26、(半角模型)(1)延长CB到H,使BH=DF,证出△AEH≌△AEF即可
(2)与第一问相同做法和思路
(3)在BC上截取BH=DF,证出△AEH≌△AEF即可证出:BE=EF+DF
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
