2021-2022学年沪科版数学七年级上册4.3线段的长短比较 同步课时作业 (word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版数学七年级上册4.3线段的长短比较 同步课时作业 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 127.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 21:38:03 | ||
图片预览




文档简介
4.3 线段的长短比较
知识点
1 线段的长短比较
1.如图1所示,已知点C,D在线段AB上,则下列线段长短关系中不正确的是
( )
图1
A.ACB.AD>CD
C.ACD.AB>CD
2.体育课上,小悦在点O处进行了四次铅球试投,铅球分别落在图2中的点M,N,P,Q处,则表示她最好成绩的落点是
( )
图2
A.点M
B.点N
C.点P
D.点Q
3.有不在同一条直线上的两条线段AB和CD,李明很难判断出它们的长短,因此他借助于圆规,操作如图3.由此可得出AB CD(填“>”“<”或“=”).?
图3
知识点
2 线段的和差
4.[教材练习第2题变式]
如图4,B,C是线段AD上不同的两点,那么:
图4
(1)BD=BC+ ,AD= + + ;?
(2)AB= -BC=AD- .?
5.如图5,已知AB=7,AP=4,OB=5,则OP的长是
( )
图5
A.1
B.2
C.3
D.4
知识点
3 线段的中点
6.如图6,C是线段AB的中点,则
图6
(1)AC= = ;?
(2)AB= +BC= AC=2BC.?
7.点M在线段AB上,给出下列四个条件,其中不能判定点M是线段AB中点的是
( )
A.AM=BM
B.AB=2AM
C.BM=AB
D.AM+BM=AB
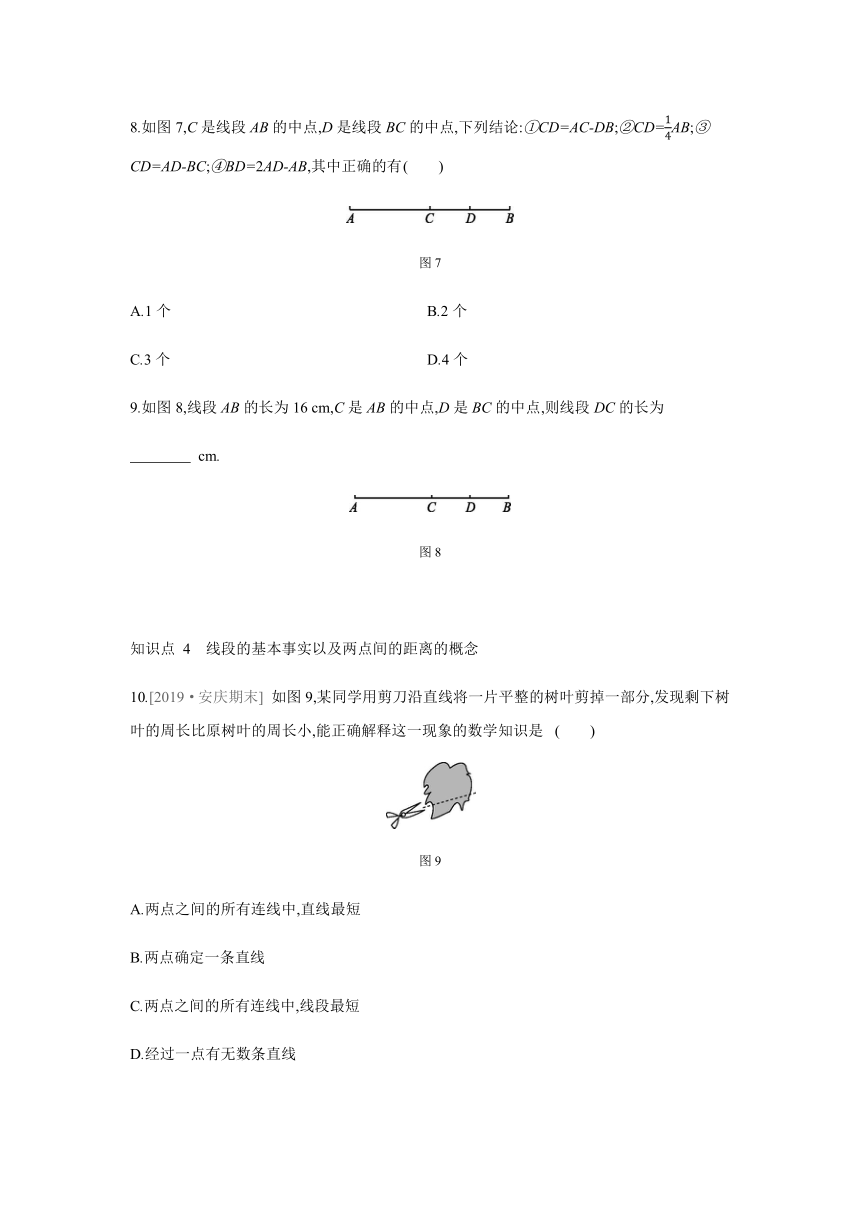
8.如图7,C是线段AB的中点,D是线段BC的中点,下列结论:①CD=AC-DB;②CD=AB;③CD=AD-BC;④BD=2AD-AB,其中正确的有
( )
图7
A.1个
B.2个
C.3个
D.4个
9.如图8,线段AB的长为16
cm,C是AB的中点,D是BC的中点,则线段DC的长为
cm.?
图8
知识点
4 线段的基本事实以及两点间的距离的概念
10.[2019·安庆期末]
如图9,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是
( )
图9
A.两点之间的所有连线中,直线最短
B.两点确定一条直线
C.两点之间的所有连线中,线段最短
D.经过一点有无数条直线
11.有下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用基本事实“两点之间的所有连线中,线段最短”来解释的是
( )
A.①②
B.①③
C.②④
D.③④
12.如图10,C,D是线段AB上的两点,E是AC的中点,F是BD的中点,若AB=10,CD=4,则EF的长为
( )
图10
A.6
B.7
C.5
D.8
13.[2019·潜山期末]
下列条件中,能判定A,B,C三点共线的是
( )
A.AB=6,AC=2,BC=5
B.AB=6,AC=2,BC=4
C.AB=6,AC=3,BC=4
D.AB=6,AC=5,BC=4
14.[2019·阜阳颍东区期末]
如图11,C,D为线段AB上两点,AC+BD=a,且AD+BC=AB,则CD等于
( )
图11
A.a
B.a
C.a
D.a
15.已知线段MN=10
cm,C是直线MN上一点,线段NC=4
cm.若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长是
.?
16.如图12,A,B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,则抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站P的位置,并说明你的理由.
图12
17.[2019·合肥包河区期末]
已知线段MN=2,Q是线段MN的中点,先按要求画出图形,再解决问题.
(1)反向延长线段MN至点A,使AM=3MN,延长线段MN至点B,使BN=BM;
(2)求线段BQ的长度;
(3)若P是线段AM的中点,求线段PQ的长.
18例:如图13,线段AB=2BC,AD=AB,M是AD的中点,N是AC的中点,试比较MN和AB+NB的大小.
图13
19变式:如图14,已知线段AB∶BC∶CD=2∶3∶4,E,F分别是AB和CD的中点,且EF=12
cm,求线段AD的长.
图14
答案
1.C [解析]
由图可知,点D在线段AC的延长线上,所以AD>AC;因为点C在线段AD上,所以AD>CD;观察图形无法判断AC与BC的大小关系;因为CD是线段AB的一部分,所以AB>CD.故选C.
2.C [解析]
如图所示,OP>ON>OQ>OM,
所以表示她最好成绩的落点是点P.故选C.
3.>
4.(1)CD AB BC CD (2)AC BD
5.B [解析]
OP=OB-PB=OB-(AB-AP)=5-(7-4)=2.
6.(1)BC AB (2)AC 2
7.D [解析]
A项,由AM=BM可以判定点M是线段AB的中点,所以此结论正确;
B项,由AB=2AM可以判定点M是线段AB的中点,所以此结论正确;
C项,由BM=AB可以判定点M是线段AB的中点,所以此结论正确;
D项,由AM+BM=AB不可以判定点M是线段AB的中点,所以此结论不正确.
故选D.
8.C [解析]
根据线段中点的定义即可判断①②③正确.
因为C是AB的中点,D是BC的中点,
所以AC=BC=AB,CD=BD=BC=AC,
所以①CD=BC-DB=AC-DB,正确;
②CD=BC=AB,正确;
③CD=AD-AC=AD-BC,正确;
④BD=AB-AD≠2AD-AB,错误.
所以正确的有①②③,共3个.
故选C.
9.4 [解析]
因为D是BC的中点,所以DC=BC.因为C是AB的中点,所以BC=AB,所以DC=AB.又因为AB=16
cm,所以DC=4
cm.
10.C [解析]
因为两点之间的所有连线中,线段最短,所以剩下树叶的周长比原树叶的周长小.
11.D
12.B [解析]
由线段的和差,得AC+DB=AB-CD=10-4=6.
因为E是AC的中点,
所以AE=AC.
因为F是BD的中点,
所以BF=BD,
所以AE+BF=(AC+DB)=3.
由线段的和差,得
EF=AB-(AE+BF)=10-3=7.
故选B.
13.B [解析]
A.因为2+5≠6,所以A,B,C三点不共线,故选项A错误;
B.因为2+4=6,所以A,B,C三点共线,故选项B正确;
C.因为3+4≠6,所以A,B,C三点不共线,故选项C错误;
D.因为5+4≠6,所以A,B,C三点不共线,故选项D错误.
14.B [解析]
因为AD+BC=AB=AC+CD+BD+CD,AC+BD=a,AB=AC+BD+CD,
所以(a+CD)=2CD+a,解得CD=a.
15.3
cm或7
cm [解析]
因为P是线段MN的中点,Q是线段NC的中点,
所以PN=MN=×10=5(cm),QN=NC=×4=2(cm).
(1)当点C在线段MN上时,如图①,
PQ=PN-QN=5-2=3(cm);
(2)当点C在MN的延长线上时,如图②,
PQ=PN+QN=5+2=7(cm).
综上,线段PQ的长为3
cm或7
cm.
故答案为3
cm或7
cm.
16.解:抽水站P的位置如图所示:
理由:两点之间的所有连线中,线段最短.
17.解:(1)如图①所示:
(2)因为Q是线段MN的中点,
所以NQ=MN=1.
因为BN=BM,所以BN=MN=2,
所以BQ=BN+NQ=2+1=3.
(3)如图②,因为Q是线段MN的中点,
所以MQ=MN=1.
因为AM=3MN,所以AM=6.
因为P是线段AM的中点,
所以PM=AM=3,
所以PQ=PM+MQ=3+1=4.
“串”题训练
例:解:设BC=x,
因为AB=2BC,AD=AB,
所以AB=2x,AD=×2x=3x,
所以AC=AB+BC=2x+x=3x.
因为M是AD的中点,N是AC的中点,
所以AM=AD=×3x=1.5x,
AN=AC=×3x=1.5x,
所以MN=AM+AN=1.5x+1.5x=3x,NB=AB-AN=2x-1.5x=0.5x,
所以AB+NB=2x+0.5x=2.5x,
所以MN>AB+NB.
变式:解:因为线段AB∶BC∶CD=2∶3∶4,所以设AB=2x
cm,BC=3x
cm,CD=4x
cm.
因为E,F分别是AB和CD的中点,
所以BE=AB=x
cm,CF=CD=2x
cm.
因为EF=12
cm,
所以EF=BE+BC+CF=12
cm,
即x+3x+2x=12,
解得x=2,
所以AD=AB+BC+CD=2x+3x+4x=9x=18(cm),
即线段AD的长为18
cm.
知识点
1 线段的长短比较
1.如图1所示,已知点C,D在线段AB上,则下列线段长短关系中不正确的是
( )
图1
A.AC
C.AC
2.体育课上,小悦在点O处进行了四次铅球试投,铅球分别落在图2中的点M,N,P,Q处,则表示她最好成绩的落点是
( )
图2
A.点M
B.点N
C.点P
D.点Q
3.有不在同一条直线上的两条线段AB和CD,李明很难判断出它们的长短,因此他借助于圆规,操作如图3.由此可得出AB CD(填“>”“<”或“=”).?
图3
知识点
2 线段的和差
4.[教材练习第2题变式]
如图4,B,C是线段AD上不同的两点,那么:
图4
(1)BD=BC+ ,AD= + + ;?
(2)AB= -BC=AD- .?
5.如图5,已知AB=7,AP=4,OB=5,则OP的长是
( )
图5
A.1
B.2
C.3
D.4
知识点
3 线段的中点
6.如图6,C是线段AB的中点,则
图6
(1)AC= = ;?
(2)AB= +BC= AC=2BC.?
7.点M在线段AB上,给出下列四个条件,其中不能判定点M是线段AB中点的是
( )
A.AM=BM
B.AB=2AM
C.BM=AB
D.AM+BM=AB
8.如图7,C是线段AB的中点,D是线段BC的中点,下列结论:①CD=AC-DB;②CD=AB;③CD=AD-BC;④BD=2AD-AB,其中正确的有
( )
图7
A.1个
B.2个
C.3个
D.4个
9.如图8,线段AB的长为16
cm,C是AB的中点,D是BC的中点,则线段DC的长为
cm.?
图8
知识点
4 线段的基本事实以及两点间的距离的概念
10.[2019·安庆期末]
如图9,某同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长小,能正确解释这一现象的数学知识是
( )
图9
A.两点之间的所有连线中,直线最短
B.两点确定一条直线
C.两点之间的所有连线中,线段最短
D.经过一点有无数条直线
11.有下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用基本事实“两点之间的所有连线中,线段最短”来解释的是
( )
A.①②
B.①③
C.②④
D.③④
12.如图10,C,D是线段AB上的两点,E是AC的中点,F是BD的中点,若AB=10,CD=4,则EF的长为
( )
图10
A.6
B.7
C.5
D.8
13.[2019·潜山期末]
下列条件中,能判定A,B,C三点共线的是
( )
A.AB=6,AC=2,BC=5
B.AB=6,AC=2,BC=4
C.AB=6,AC=3,BC=4
D.AB=6,AC=5,BC=4
14.[2019·阜阳颍东区期末]
如图11,C,D为线段AB上两点,AC+BD=a,且AD+BC=AB,则CD等于
( )
图11
A.a
B.a
C.a
D.a
15.已知线段MN=10
cm,C是直线MN上一点,线段NC=4
cm.若P是线段MN的中点,Q是线段NC的中点,则线段PQ的长是
.?
16.如图12,A,B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,则抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站P的位置,并说明你的理由.
图12
17.[2019·合肥包河区期末]
已知线段MN=2,Q是线段MN的中点,先按要求画出图形,再解决问题.
(1)反向延长线段MN至点A,使AM=3MN,延长线段MN至点B,使BN=BM;
(2)求线段BQ的长度;
(3)若P是线段AM的中点,求线段PQ的长.
18例:如图13,线段AB=2BC,AD=AB,M是AD的中点,N是AC的中点,试比较MN和AB+NB的大小.
图13
19变式:如图14,已知线段AB∶BC∶CD=2∶3∶4,E,F分别是AB和CD的中点,且EF=12
cm,求线段AD的长.
图14
答案
1.C [解析]
由图可知,点D在线段AC的延长线上,所以AD>AC;因为点C在线段AD上,所以AD>CD;观察图形无法判断AC与BC的大小关系;因为CD是线段AB的一部分,所以AB>CD.故选C.
2.C [解析]
如图所示,OP>ON>OQ>OM,
所以表示她最好成绩的落点是点P.故选C.
3.>
4.(1)CD AB BC CD (2)AC BD
5.B [解析]
OP=OB-PB=OB-(AB-AP)=5-(7-4)=2.
6.(1)BC AB (2)AC 2
7.D [解析]
A项,由AM=BM可以判定点M是线段AB的中点,所以此结论正确;
B项,由AB=2AM可以判定点M是线段AB的中点,所以此结论正确;
C项,由BM=AB可以判定点M是线段AB的中点,所以此结论正确;
D项,由AM+BM=AB不可以判定点M是线段AB的中点,所以此结论不正确.
故选D.
8.C [解析]
根据线段中点的定义即可判断①②③正确.
因为C是AB的中点,D是BC的中点,
所以AC=BC=AB,CD=BD=BC=AC,
所以①CD=BC-DB=AC-DB,正确;
②CD=BC=AB,正确;
③CD=AD-AC=AD-BC,正确;
④BD=AB-AD≠2AD-AB,错误.
所以正确的有①②③,共3个.
故选C.
9.4 [解析]
因为D是BC的中点,所以DC=BC.因为C是AB的中点,所以BC=AB,所以DC=AB.又因为AB=16
cm,所以DC=4
cm.
10.C [解析]
因为两点之间的所有连线中,线段最短,所以剩下树叶的周长比原树叶的周长小.
11.D
12.B [解析]
由线段的和差,得AC+DB=AB-CD=10-4=6.
因为E是AC的中点,
所以AE=AC.
因为F是BD的中点,
所以BF=BD,
所以AE+BF=(AC+DB)=3.
由线段的和差,得
EF=AB-(AE+BF)=10-3=7.
故选B.
13.B [解析]
A.因为2+5≠6,所以A,B,C三点不共线,故选项A错误;
B.因为2+4=6,所以A,B,C三点共线,故选项B正确;
C.因为3+4≠6,所以A,B,C三点不共线,故选项C错误;
D.因为5+4≠6,所以A,B,C三点不共线,故选项D错误.
14.B [解析]
因为AD+BC=AB=AC+CD+BD+CD,AC+BD=a,AB=AC+BD+CD,
所以(a+CD)=2CD+a,解得CD=a.
15.3
cm或7
cm [解析]
因为P是线段MN的中点,Q是线段NC的中点,
所以PN=MN=×10=5(cm),QN=NC=×4=2(cm).
(1)当点C在线段MN上时,如图①,
PQ=PN-QN=5-2=3(cm);
(2)当点C在MN的延长线上时,如图②,
PQ=PN+QN=5+2=7(cm).
综上,线段PQ的长为3
cm或7
cm.
故答案为3
cm或7
cm.
16.解:抽水站P的位置如图所示:
理由:两点之间的所有连线中,线段最短.
17.解:(1)如图①所示:
(2)因为Q是线段MN的中点,
所以NQ=MN=1.
因为BN=BM,所以BN=MN=2,
所以BQ=BN+NQ=2+1=3.
(3)如图②,因为Q是线段MN的中点,
所以MQ=MN=1.
因为AM=3MN,所以AM=6.
因为P是线段AM的中点,
所以PM=AM=3,
所以PQ=PM+MQ=3+1=4.
“串”题训练
例:解:设BC=x,
因为AB=2BC,AD=AB,
所以AB=2x,AD=×2x=3x,
所以AC=AB+BC=2x+x=3x.
因为M是AD的中点,N是AC的中点,
所以AM=AD=×3x=1.5x,
AN=AC=×3x=1.5x,
所以MN=AM+AN=1.5x+1.5x=3x,NB=AB-AN=2x-1.5x=0.5x,
所以AB+NB=2x+0.5x=2.5x,
所以MN>AB+NB.
变式:解:因为线段AB∶BC∶CD=2∶3∶4,所以设AB=2x
cm,BC=3x
cm,CD=4x
cm.
因为E,F分别是AB和CD的中点,
所以BE=AB=x
cm,CF=CD=2x
cm.
因为EF=12
cm,
所以EF=BE+BC+CF=12
cm,
即x+3x+2x=12,
解得x=2,
所以AD=AB+BC+CD=2x+3x+4x=9x=18(cm),
即线段AD的长为18
cm.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
