2021-2022学年沪科版数学七年级上册4.1几何图形 同步课时作业(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版数学七年级上册4.1几何图形 同步课时作业(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 200.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 21:40:46 | ||
图片预览



文档简介
4.1 几何图形
知识点
1 几何图形的认识
1.下列图形中是平面图形的是
( )
图1
2.图2中,立体图形的个数是
( )
图2
A.2
B.3
C.4
D.5
3.[2019·北京一模]
下列几何体中,是圆锥的为( )
图3
4.下列哪个物体给我们以圆柱的形象
( )
图4
5.篮球、排球、羽毛球、足球、乒乓球中,所呈现出的几何图形不是球的是
.?
6.观察实物图(如图5),写出与它们类似的几何图形的名称.
图5
知识点
2 几何图形的构成元素
7.下列几何体中,全是由曲的面围成的是
( )
A.圆锥
B.正方体
C.圆柱
D.球
8.[2019·宁德期中]
“笔尖在纸上快速滑动写出数字6”,运用数学知识解释这一现象是
( )
A.点动成线
B.线动成面
C.面动成体
D.面与面相交得线
9.下面现象能说明“线动成面”的是
( )
A.旋转一扇门,门在空中运动的痕迹
B.扔一块小石子,小石子在空中飞行的路线
C.天空划过一道流星
D.汽车雨刷在挡风玻璃上面画出的痕迹
10.[2019·南宁]
将图6中的平面图形绕直线l旋转一周,得到的立体图形是
( )
图6
图7
11.一个多面体的模型如图8所示,观察这个模型,回答下列问题:
图8
(1)这个多面体有 个顶点,经过每个顶点有 条棱;?
(2)这个多面体有 条棱,每条棱是由 个面相交形成的;?
(3)这个多面体有 个侧面,
个底面,它们分别属于几何图形中的
和 ,它们都是
(填“平的面”或“曲的面”).?
12.从四面体的一个顶点发出的棱有
( )
A.3条
B.4条
C.5条
D.6条
13.有一个几何体模型,两位同学观察该模型并描述它的特征.甲同学:它有7个面;乙同学:它有10个顶点.该模型的形状对应的立体图形可能是( )
A.四棱柱
B.五棱柱
C.六棱柱
D.七棱柱
14.如图9,这个几何体是由几个面组成的?面与面相交形成几条线?其中有几条线是曲的?
图9
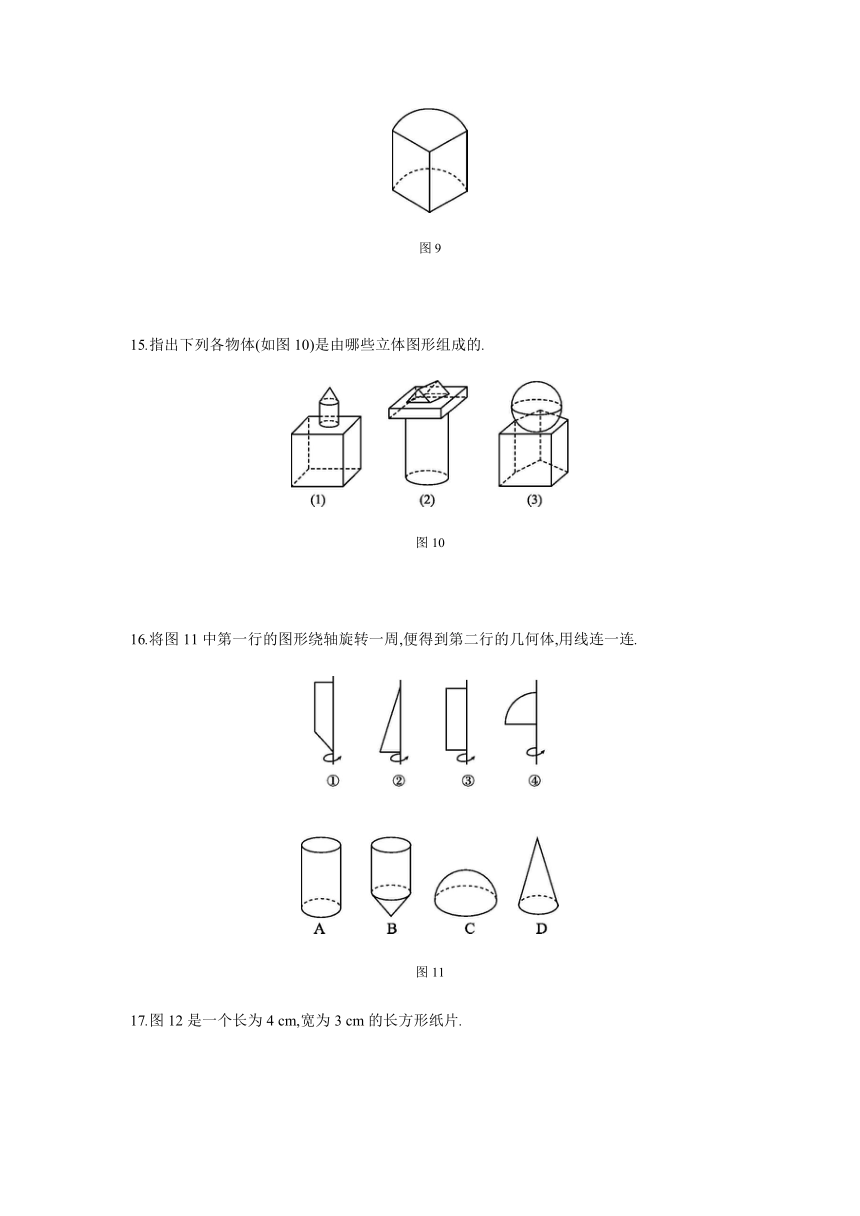
15.指出下列各物体(如图10)是由哪些立体图形组成的.
图10
16.将图11中第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
图11
17.图12是一个长为4
cm,宽为3
cm的长方形纸片.
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 ;?
(2)当此长方形纸片绕长边所在直线旋转一周时(如图②),求所形成的几何体的体积;
(3)当此长方形纸片绕短边所在直线旋转一周时(如图③),求所形成的几何体的体积.
图12
18.数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型(如图13),解答后面的问题:
图13
(1)根据上面的多面体模型,完成表格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
6
12
八面体
8
12
十二面体
20
12
30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 ;?
(2)一个多面体的面数与顶点数相等,且有12条棱,则这个多面体的面数是 ;?
(3)某个玻璃饰品的外形是简单多面体,它的外表面由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.
答案
1.A 2.B
3.D [解析]
A.是长方体(四棱柱),不合题意;
B.是三棱锥,不合题意;
C.是圆柱,不合题意;
D.是圆锥,符合题意.
4.C [解析]
A.此物体给我们以圆锥的形象;
B.此物体给我们以正方体的形象;
C.此物体给我们以圆柱的形象;
D.此物体给我们以球的形象.
5.羽毛球 [解析]
羽毛球的形状不能呈现出球.
6.长方体 圆柱 球 六棱柱 [解析]
立体图形源于生活,要能从生活中把它抽象出来.
7.D
8.A [解析]
笔尖在纸上快速滑动写出数字6,用数学知识解释为点动成线.
9.D [解析]
A.旋转一扇门,门在空中运动的痕迹是“面动成体”,故本选项错误;
B.扔一块小石子,小石子在空中飞行的路线是“点动成线”,故本选项错误;
C.天空划过一道流星是“点动成线”,故本选项错误;
D.汽车雨刷在挡风玻璃上面画出的痕迹是“线动成面”,故本选项正确.
10.D [解析]
面动成体,直角三角形绕直角边所在直线旋转一周可得圆锥,长方形绕一边所在直线旋转一周可得圆柱,那么所求的图形是下面是圆锥,上面是圆柱的组合图形.
11.(1)12 3
(2)18 2
(3)6 2 四边形 六边形 平的面
12.A
13.B [解析]
五棱柱的两个底面是五边形,侧面是五个四边形,共有7个面.五棱柱有10个顶点.
14.解:这个几何体是由5个面组成的,面与面相交形成9条线,其中有2条线是曲的.
15.解:(1)由正方体、圆柱、圆锥组成.
(2)由圆柱、长方体、三棱柱组成.
(3)由五棱柱、球组成.
16.解:①—B,②—D,③—A,④—C.
17.解:(1)圆柱 面动成体
(2)绕长边所在直线旋转一周得到的圆柱的底面半径为3
cm,高为4
cm,几何体的体积=π×32×4=36π(cm3).
(3)绕短边所在直线旋转一周得到的圆柱的底面半径为4
cm,高为3
cm,几何体的体积=π×42×3=48π(cm3).
18.解:(1)
第一行:6 第三行:6 V+F-E=2
(2)7
(3)这个多面体的面数为F=x+y,
棱数为=36,
根据V+F-E=2,可得24+(x+y)-36=2,
所以x+y=14.
知识点
1 几何图形的认识
1.下列图形中是平面图形的是
( )
图1
2.图2中,立体图形的个数是
( )
图2
A.2
B.3
C.4
D.5
3.[2019·北京一模]
下列几何体中,是圆锥的为( )
图3
4.下列哪个物体给我们以圆柱的形象
( )
图4
5.篮球、排球、羽毛球、足球、乒乓球中,所呈现出的几何图形不是球的是
.?
6.观察实物图(如图5),写出与它们类似的几何图形的名称.
图5
知识点
2 几何图形的构成元素
7.下列几何体中,全是由曲的面围成的是
( )
A.圆锥
B.正方体
C.圆柱
D.球
8.[2019·宁德期中]
“笔尖在纸上快速滑动写出数字6”,运用数学知识解释这一现象是
( )
A.点动成线
B.线动成面
C.面动成体
D.面与面相交得线
9.下面现象能说明“线动成面”的是
( )
A.旋转一扇门,门在空中运动的痕迹
B.扔一块小石子,小石子在空中飞行的路线
C.天空划过一道流星
D.汽车雨刷在挡风玻璃上面画出的痕迹
10.[2019·南宁]
将图6中的平面图形绕直线l旋转一周,得到的立体图形是
( )
图6
图7
11.一个多面体的模型如图8所示,观察这个模型,回答下列问题:
图8
(1)这个多面体有 个顶点,经过每个顶点有 条棱;?
(2)这个多面体有 条棱,每条棱是由 个面相交形成的;?
(3)这个多面体有 个侧面,
个底面,它们分别属于几何图形中的
和 ,它们都是
(填“平的面”或“曲的面”).?
12.从四面体的一个顶点发出的棱有
( )
A.3条
B.4条
C.5条
D.6条
13.有一个几何体模型,两位同学观察该模型并描述它的特征.甲同学:它有7个面;乙同学:它有10个顶点.该模型的形状对应的立体图形可能是( )
A.四棱柱
B.五棱柱
C.六棱柱
D.七棱柱
14.如图9,这个几何体是由几个面组成的?面与面相交形成几条线?其中有几条线是曲的?
图9
15.指出下列各物体(如图10)是由哪些立体图形组成的.
图10
16.将图11中第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
图11
17.图12是一个长为4
cm,宽为3
cm的长方形纸片.
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 ;?
(2)当此长方形纸片绕长边所在直线旋转一周时(如图②),求所形成的几何体的体积;
(3)当此长方形纸片绕短边所在直线旋转一周时(如图③),求所形成的几何体的体积.
图12
18.数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型(如图13),解答后面的问题:
图13
(1)根据上面的多面体模型,完成表格:
多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
6
12
八面体
8
12
十二面体
20
12
30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 ;?
(2)一个多面体的面数与顶点数相等,且有12条棱,则这个多面体的面数是 ;?
(3)某个玻璃饰品的外形是简单多面体,它的外表面由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.
答案
1.A 2.B
3.D [解析]
A.是长方体(四棱柱),不合题意;
B.是三棱锥,不合题意;
C.是圆柱,不合题意;
D.是圆锥,符合题意.
4.C [解析]
A.此物体给我们以圆锥的形象;
B.此物体给我们以正方体的形象;
C.此物体给我们以圆柱的形象;
D.此物体给我们以球的形象.
5.羽毛球 [解析]
羽毛球的形状不能呈现出球.
6.长方体 圆柱 球 六棱柱 [解析]
立体图形源于生活,要能从生活中把它抽象出来.
7.D
8.A [解析]
笔尖在纸上快速滑动写出数字6,用数学知识解释为点动成线.
9.D [解析]
A.旋转一扇门,门在空中运动的痕迹是“面动成体”,故本选项错误;
B.扔一块小石子,小石子在空中飞行的路线是“点动成线”,故本选项错误;
C.天空划过一道流星是“点动成线”,故本选项错误;
D.汽车雨刷在挡风玻璃上面画出的痕迹是“线动成面”,故本选项正确.
10.D [解析]
面动成体,直角三角形绕直角边所在直线旋转一周可得圆锥,长方形绕一边所在直线旋转一周可得圆柱,那么所求的图形是下面是圆锥,上面是圆柱的组合图形.
11.(1)12 3
(2)18 2
(3)6 2 四边形 六边形 平的面
12.A
13.B [解析]
五棱柱的两个底面是五边形,侧面是五个四边形,共有7个面.五棱柱有10个顶点.
14.解:这个几何体是由5个面组成的,面与面相交形成9条线,其中有2条线是曲的.
15.解:(1)由正方体、圆柱、圆锥组成.
(2)由圆柱、长方体、三棱柱组成.
(3)由五棱柱、球组成.
16.解:①—B,②—D,③—A,④—C.
17.解:(1)圆柱 面动成体
(2)绕长边所在直线旋转一周得到的圆柱的底面半径为3
cm,高为4
cm,几何体的体积=π×32×4=36π(cm3).
(3)绕短边所在直线旋转一周得到的圆柱的底面半径为4
cm,高为3
cm,几何体的体积=π×42×3=48π(cm3).
18.解:(1)
第一行:6 第三行:6 V+F-E=2
(2)7
(3)这个多面体的面数为F=x+y,
棱数为=36,
根据V+F-E=2,可得24+(x+y)-36=2,
所以x+y=14.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
