重庆市部分区2020-2021学年高二下学期期末联考数学试题 Word版含答案
文档属性
| 名称 | 重庆市部分区2020-2021学年高二下学期期末联考数学试题 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 609.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 00:00:00 | ||
图片预览




文档简介
重庆市部分区2020-2021学年度第二学期期末联考
高二数学试题卷
一?选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2. 某物体的位移s(米)与时间t(秒)的关系为,则该物体在2秒末的瞬时速度是( )
A. 12米/秒 B. 10米/秒 C. 8米/秒 D. 6米/秒
3. 从2021年3月24日起,中国启动新冠疫苗接种数据的日报制度,国家卫健委每日在官网公布疫苗接种总数,这也是人类疫苗接种史上首次启动国家级最大规模的日报制度.为了方便广大市民接种新冠疫苗,提高新冠疫苗接种普及率,重庆市某区卫健委在城区设立了11个接种点,在乡镇设立了19个接种点.某市民为了在同一接种点顺利完成新冠疫苗接种,则不同接种点的选法共有( )
A. 11种 B. 19种 C. 30种 D. 209种
4. 若,则随机变量X的期望( )
A. B. 2 C. D. 3
5. 二项式的展开式中常数项是( )
A. B. 160 C. D. 20
6. 函数的图象在点处的切线方程是( )
A. B.
C. D.
7. 某次数学考试的一道多项选择“题”的要求是:“在每小题给出的四个选项中,全部选对的得5分,部分选对的得2分,有选错的得0分.”已知该选择“题”的正确答案是CD,且甲?乙?丙?丁四位同学都不会做,下列表述正确的是( )
A. 甲同学仅随机选一个选项,能得2分的概率是
B. 乙同学仅随机选两个选项,能得5分的概率是
C. 丙同学随机选择选项,能得分的概率是
D. 丁同学随机至少选择两个选项,能得分的概率是
8. 已知函数,,若对任意,存在,使,则实数b的取值范围是( )
A. B. C. D.
二?多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知复数z满足,则下列说法正确的是( )
A. z的共轭复数是 B.
C. z的虚部是 D.
10. 习近平总书记在党史学习教育动员大会上讲话强调,“要抓好青少年学习教育,着力讲好党的故事?革命的故事?英雄的故事,厚植爱党?爱国?爱社会主义的情感,让红色基因?革命薪火代代传承.”为了深入贯彻习近平总书记的讲话精神,我校积极开展党史学习教育,举行“学党史,颂党恩,跟党走”的主题宣讲.现安排4名教师到高中3个年级进行宣讲,每个年级至少1名教师,则不同的选法有( )
A. B. C. D.
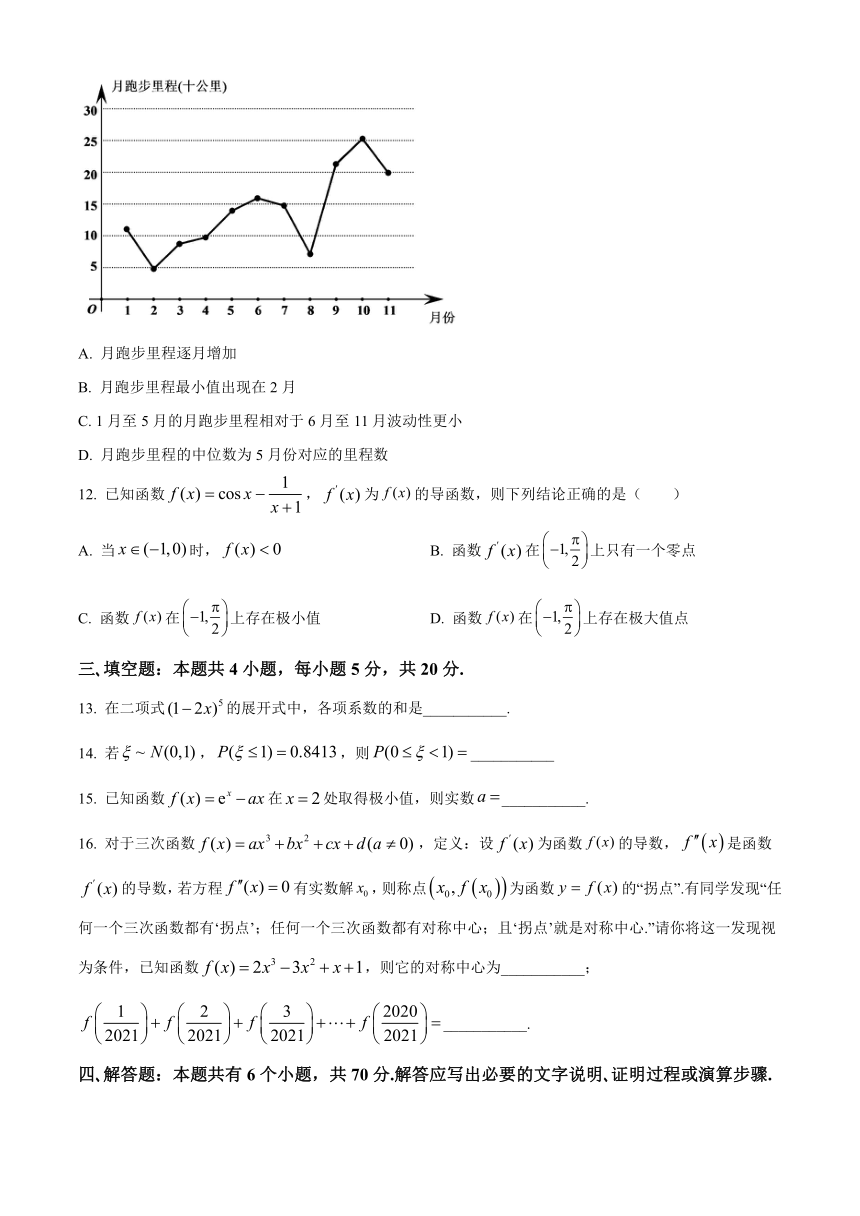
11. 跑步爱好者小亮为了参加“2021年重庆市第六届运动会半程马拉松”比赛,从2020年1月开始进行长跑训练.他根据某跑步软件记录2020年1月至2020年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图.请根据该折线图分析,下列结论正确的是( )
A. 月跑步里程逐月增加
B. 月跑步里程最小值出现在2月
C. 1月至5月的月跑步里程相对于6月至11月波动性更小
D. 月跑步里程的中位数为5月份对应的里程数
12. 已知函数,为的导函数,则下列结论正确的是( )
A. 当时, B. 函数在上只有一个零点
C. 函数在上存在极小值 D. 函数在上存在极大值点
三?填空题:本题共4小题,每小题5分,共20分.
13. 在二项式的展开式中,各项系数的和是___________.
14. 若,,则___________
15. 已知函数在处取得极小值,则实数___________.
16. 对于三次函数,定义:设为函数的导数,是函数的导数,若方程有实数解,则称点为函数的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,已知函数,则它的对称中心为___________;___________.
四?解答题:本题共有6个小题,共70分.解答应写出必要的文字说明?证明过程或演算步骤.
17. 己知的二项展开式中二项式系数之和为512.
(1)求n的值;
(2)求展开式中项的系数.
18. 已知函数
(1)求函数单调区间;
(2)求函数在区间上的最大值和最小值.
19. 新疆是歌舞之乡、瓜果之乡、黄金玉石之邦.在新疆种植棉花有着得天独厚的自然条件,土质呈碱性,夏季温差大,阳光充足,光合作用充分,生长时间长,这种环境下种植的棉花绒长?品质好?产量高,所以新疆棉花举世闻名.当地政府为了更好地向全世界推广宣传新疆棉花,需要大致了解新疆棉花的产量.通过调查发现新疆地区近几年的棉花产量统计如下表:
年份
年份代码
棉花产量 (百万吨)
(1)根据表中数据,建立关于的线性回归方程;
(2)请你根据(1)中的线性回归方程预测今年()新疆棉花的产量.
参考公式:,.
20. 控烟行动是健康中国重庆行动15项行动之一.2020年9月29日,重庆市五届人大常委会第二十一次会议举行第二次全体会议,表决通过《重庆市公共场所控制吸烟条例》,自2021年1月1日起施行.本条例所称的公共场所,是指公众可以进出的场所或供集体使用的场所,包括餐饮服务场所?住宿休息场所?公众娱乐场所?工作场所?公共交通工具?公用电梯等.为了解重庆某区市民能否自觉遵守该条例,某调查机构借助网络进行了问卷调查,并从参与调查的市民中抽取了200人进行抽样分析,得到如下列联表(单位:人):
能自觉遵守该条例 不能自觉遵守该条例 总计
50岁及以下 90 30 120
50岁以上 50 30 80
总计 140 60 200
(1)根据以上数据,判断是否有90%的把握认为该区市民能否自觉遵守该条例与年龄有关?
(2)将频率视为概率,现从该区50岁及以下的市民中用随机抽样的方法每次抽取1人,共抽取3次.记被抽取的3人中“不能自觉遵守该条例”的人数为X,若每次抽取的结果是相互独立的,求随机变量X的分布列.
附:,其中.
0.15 0.10 0.05 0.025
2.072 2.706 3.841 5.024
21. 小张?小王两人进行羽毛球比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局小张获胜的概率为,小王获胜的概率为,各局比赛结果相互独立.
(1)求小张在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列和均值.
22. 已知函数.
(1)若曲线在点处的切线与直线垂直,求m的值:
(2)若对于都有成立,试求m的取值范围;
(3)记,当时,函数在区间上有两个零点,求实数n的取值范围.
重庆市部分区2020-2021学年度第二学期期末联考
高二数学试题卷 答案版
一?选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
【答案】D
2. 某物体的位移s(米)与时间t(秒)的关系为,则该物体在2秒末的瞬时速度是( )
A. 12米/秒 B. 10米/秒 C. 8米/秒 D. 6米/秒
【答案】B
3. 从2021年3月24日起,中国启动新冠疫苗接种数据的日报制度,国家卫健委每日在官网公布疫苗接种总数,这也是人类疫苗接种史上首次启动国家级最大规模的日报制度.为了方便广大市民接种新冠疫苗,提高新冠疫苗接种普及率,重庆市某区卫健委在城区设立了11个接种点,在乡镇设立了19个接种点.某市民为了在同一接种点顺利完成新冠疫苗接种,则不同接种点的选法共有( )
A. 11种 B. 19种 C. 30种 D. 209种
【答案】C
4. 若,则随机变量X的期望( )
A. B. 2 C. D. 3
【答案】D
5. 二项式的展开式中常数项是( )
A. B. 160 C. D. 20
【答案】A
6. 函数的图象在点处的切线方程是( )
A. B.
C. D.
【答案】C
7. 某次数学考试的一道多项选择“题”的要求是:“在每小题给出的四个选项中,全部选对的得5分,部分选对的得2分,有选错的得0分.”已知该选择“题”的正确答案是CD,且甲?乙?丙?丁四位同学都不会做,下列表述正确的是( )
A. 甲同学仅随机选一个选项,能得2分的概率是
B. 乙同学仅随机选两个选项,能得5分的概率是
C. 丙同学随机选择选项,能得分的概率是
D. 丁同学随机至少选择两个选项,能得分的概率是
【答案】B
8. 已知函数,,若对任意,存在,使,则实数b的取值范围是( )
A. B. C. D.
【答案】C
二?多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知复数z满足,则下列说法正确的是( )
A. z的共轭复数是 B.
C. z的虚部是 D.
【答案】AB
10. 习近平总书记在党史学习教育动员大会上讲话强调,“要抓好青少年学习教育,着力讲好党的故事?革命的故事?英雄的故事,厚植爱党?爱国?爱社会主义的情感,让红色基因?革命薪火代代传承.”为了深入贯彻习近平总书记的讲话精神,我校积极开展党史学习教育,举行“学党史,颂党恩,跟党走”的主题宣讲.现安排4名教师到高中3个年级进行宣讲,每个年级至少1名教师,则不同的选法有( )
A. B. C. D.
【答案】BD
11. 跑步爱好者小亮为了参加“2021年重庆市第六届运动会半程马拉松”比赛,从2020年1月开始进行长跑训练.他根据某跑步软件记录2020年1月至2020年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图.请根据该折线图分析,下列结论正确的是( )
A. 月跑步里程逐月增加
B. 月跑步里程最小值出现在2月
C. 1月至5月的月跑步里程相对于6月至11月波动性更小
D. 月跑步里程的中位数为5月份对应的里程数
【答案】BCD
12. 已知函数,为的导函数,则下列结论正确的是( )
A. 当时, B. 函数在上只有一个零点
C. 函数在上存在极小值 D. 函数在上存在极大值点
【答案】ABD
三?填空题:本题共4小题,每小题5分,共20分.
13. 在二项式的展开式中,各项系数的和是___________.
【答案】
14. 若,,则___________
【答案】03413
15. 已知函数在处取得极小值,则实数___________.
【答案】
16. 对于三次函数,定义:设为函数的导数,是函数的导数,若方程有实数解,则称点为函数的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,已知函数,则它的对称中心为___________;___________.
【答案】 ①. ②.
四?解答题:本题共有6个小题,共70分.解答应写出必要的文字说明?证明过程或演算步骤.
17. 己知的二项展开式中二项式系数之和为512.
(1)求n的值;
(2)求展开式中项的系数.
【答案】(1);(2)
18. 已知函数
(1)求函数单调区间;
(2)求函数在区间上的最大值和最小值.
【答案】(1)增区间:,,减区间:;(2),
19. 新疆是歌舞之乡、瓜果之乡、黄金玉石之邦.在新疆种植棉花有着得天独厚的自然条件,土质呈碱性,夏季温差大,阳光充足,光合作用充分,生长时间长,这种环境下种植的棉花绒长?品质好?产量高,所以新疆棉花举世闻名.当地政府为了更好地向全世界推广宣传新疆棉花,需要大致了解新疆棉花的产量.通过调查发现新疆地区近几年的棉花产量统计如下表:
年份
年份代码
棉花产量 (百万吨)
(1)根据表中数据,建立关于的线性回归方程;
(2)请你根据(1)中的线性回归方程预测今年()新疆棉花的产量.
参考公式:,.
【答案】(1);(2)预测今年()新疆棉花的产量约为万吨.
20. 控烟行动是健康中国重庆行动15项行动之一.2020年9月29日,重庆市五届人大常委会第二十一次会议举行第二次全体会议,表决通过《重庆市公共场所控制吸烟条例》,自2021年1月1日起施行.本条例所称的公共场所,是指公众可以进出的场所或供集体使用的场所,包括餐饮服务场所?住宿休息场所?公众娱乐场所?工作场所?公共交通工具?公用电梯等.为了解重庆某区市民能否自觉遵守该条例,某调查机构借助网络进行了问卷调查,并从参与调查的市民中抽取了200人进行抽样分析,得到如下列联表(单位:人):
能自觉遵守该条例 不能自觉遵守该条例 总计
50岁及以下 90 30 120
50岁以上 50 30 80
总计 140 60 200
(1)根据以上数据,判断是否有90%的把握认为该区市民能否自觉遵守该条例与年龄有关?
(2)将频率视为概率,现从该区50岁及以下的市民中用随机抽样的方法每次抽取1人,共抽取3次.记被抽取的3人中“不能自觉遵守该条例”的人数为X,若每次抽取的结果是相互独立的,求随机变量X的分布列.
附:,其中.
0.15 0.10 0.05 0.025
2.072 2.706 3.841 5.024
【答案】(1)有90%的把握认为该区市民能否自觉遵守该条例与年龄有关(2)答案见解析.
21. 小张?小王两人进行羽毛球比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局小张获胜的概率为,小王获胜的概率为,各局比赛结果相互独立.
(1)求小张在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列和均值.
【答案】(1);(2)分布列见解析,.
22. 已知函数.
(1)若曲线在点处的切线与直线垂直,求m的值:
(2)若对于都有成立,试求m的取值范围;
(3)记,当时,函数在区间上有两个零点,求实数n的取值范围.
【答案】(1);(2);(3).
高二数学试题卷
一?选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
2. 某物体的位移s(米)与时间t(秒)的关系为,则该物体在2秒末的瞬时速度是( )
A. 12米/秒 B. 10米/秒 C. 8米/秒 D. 6米/秒
3. 从2021年3月24日起,中国启动新冠疫苗接种数据的日报制度,国家卫健委每日在官网公布疫苗接种总数,这也是人类疫苗接种史上首次启动国家级最大规模的日报制度.为了方便广大市民接种新冠疫苗,提高新冠疫苗接种普及率,重庆市某区卫健委在城区设立了11个接种点,在乡镇设立了19个接种点.某市民为了在同一接种点顺利完成新冠疫苗接种,则不同接种点的选法共有( )
A. 11种 B. 19种 C. 30种 D. 209种
4. 若,则随机变量X的期望( )
A. B. 2 C. D. 3
5. 二项式的展开式中常数项是( )
A. B. 160 C. D. 20
6. 函数的图象在点处的切线方程是( )
A. B.
C. D.
7. 某次数学考试的一道多项选择“题”的要求是:“在每小题给出的四个选项中,全部选对的得5分,部分选对的得2分,有选错的得0分.”已知该选择“题”的正确答案是CD,且甲?乙?丙?丁四位同学都不会做,下列表述正确的是( )
A. 甲同学仅随机选一个选项,能得2分的概率是
B. 乙同学仅随机选两个选项,能得5分的概率是
C. 丙同学随机选择选项,能得分的概率是
D. 丁同学随机至少选择两个选项,能得分的概率是
8. 已知函数,,若对任意,存在,使,则实数b的取值范围是( )
A. B. C. D.
二?多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知复数z满足,则下列说法正确的是( )
A. z的共轭复数是 B.
C. z的虚部是 D.
10. 习近平总书记在党史学习教育动员大会上讲话强调,“要抓好青少年学习教育,着力讲好党的故事?革命的故事?英雄的故事,厚植爱党?爱国?爱社会主义的情感,让红色基因?革命薪火代代传承.”为了深入贯彻习近平总书记的讲话精神,我校积极开展党史学习教育,举行“学党史,颂党恩,跟党走”的主题宣讲.现安排4名教师到高中3个年级进行宣讲,每个年级至少1名教师,则不同的选法有( )
A. B. C. D.
11. 跑步爱好者小亮为了参加“2021年重庆市第六届运动会半程马拉松”比赛,从2020年1月开始进行长跑训练.他根据某跑步软件记录2020年1月至2020年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图.请根据该折线图分析,下列结论正确的是( )
A. 月跑步里程逐月增加
B. 月跑步里程最小值出现在2月
C. 1月至5月的月跑步里程相对于6月至11月波动性更小
D. 月跑步里程的中位数为5月份对应的里程数
12. 已知函数,为的导函数,则下列结论正确的是( )
A. 当时, B. 函数在上只有一个零点
C. 函数在上存在极小值 D. 函数在上存在极大值点
三?填空题:本题共4小题,每小题5分,共20分.
13. 在二项式的展开式中,各项系数的和是___________.
14. 若,,则___________
15. 已知函数在处取得极小值,则实数___________.
16. 对于三次函数,定义:设为函数的导数,是函数的导数,若方程有实数解,则称点为函数的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,已知函数,则它的对称中心为___________;___________.
四?解答题:本题共有6个小题,共70分.解答应写出必要的文字说明?证明过程或演算步骤.
17. 己知的二项展开式中二项式系数之和为512.
(1)求n的值;
(2)求展开式中项的系数.
18. 已知函数
(1)求函数单调区间;
(2)求函数在区间上的最大值和最小值.
19. 新疆是歌舞之乡、瓜果之乡、黄金玉石之邦.在新疆种植棉花有着得天独厚的自然条件,土质呈碱性,夏季温差大,阳光充足,光合作用充分,生长时间长,这种环境下种植的棉花绒长?品质好?产量高,所以新疆棉花举世闻名.当地政府为了更好地向全世界推广宣传新疆棉花,需要大致了解新疆棉花的产量.通过调查发现新疆地区近几年的棉花产量统计如下表:
年份
年份代码
棉花产量 (百万吨)
(1)根据表中数据,建立关于的线性回归方程;
(2)请你根据(1)中的线性回归方程预测今年()新疆棉花的产量.
参考公式:,.
20. 控烟行动是健康中国重庆行动15项行动之一.2020年9月29日,重庆市五届人大常委会第二十一次会议举行第二次全体会议,表决通过《重庆市公共场所控制吸烟条例》,自2021年1月1日起施行.本条例所称的公共场所,是指公众可以进出的场所或供集体使用的场所,包括餐饮服务场所?住宿休息场所?公众娱乐场所?工作场所?公共交通工具?公用电梯等.为了解重庆某区市民能否自觉遵守该条例,某调查机构借助网络进行了问卷调查,并从参与调查的市民中抽取了200人进行抽样分析,得到如下列联表(单位:人):
能自觉遵守该条例 不能自觉遵守该条例 总计
50岁及以下 90 30 120
50岁以上 50 30 80
总计 140 60 200
(1)根据以上数据,判断是否有90%的把握认为该区市民能否自觉遵守该条例与年龄有关?
(2)将频率视为概率,现从该区50岁及以下的市民中用随机抽样的方法每次抽取1人,共抽取3次.记被抽取的3人中“不能自觉遵守该条例”的人数为X,若每次抽取的结果是相互独立的,求随机变量X的分布列.
附:,其中.
0.15 0.10 0.05 0.025
2.072 2.706 3.841 5.024
21. 小张?小王两人进行羽毛球比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局小张获胜的概率为,小王获胜的概率为,各局比赛结果相互独立.
(1)求小张在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列和均值.
22. 已知函数.
(1)若曲线在点处的切线与直线垂直,求m的值:
(2)若对于都有成立,试求m的取值范围;
(3)记,当时,函数在区间上有两个零点,求实数n的取值范围.
重庆市部分区2020-2021学年度第二学期期末联考
高二数学试题卷 答案版
一?选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 在复平面内,复数对应的点位于( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
【答案】D
2. 某物体的位移s(米)与时间t(秒)的关系为,则该物体在2秒末的瞬时速度是( )
A. 12米/秒 B. 10米/秒 C. 8米/秒 D. 6米/秒
【答案】B
3. 从2021年3月24日起,中国启动新冠疫苗接种数据的日报制度,国家卫健委每日在官网公布疫苗接种总数,这也是人类疫苗接种史上首次启动国家级最大规模的日报制度.为了方便广大市民接种新冠疫苗,提高新冠疫苗接种普及率,重庆市某区卫健委在城区设立了11个接种点,在乡镇设立了19个接种点.某市民为了在同一接种点顺利完成新冠疫苗接种,则不同接种点的选法共有( )
A. 11种 B. 19种 C. 30种 D. 209种
【答案】C
4. 若,则随机变量X的期望( )
A. B. 2 C. D. 3
【答案】D
5. 二项式的展开式中常数项是( )
A. B. 160 C. D. 20
【答案】A
6. 函数的图象在点处的切线方程是( )
A. B.
C. D.
【答案】C
7. 某次数学考试的一道多项选择“题”的要求是:“在每小题给出的四个选项中,全部选对的得5分,部分选对的得2分,有选错的得0分.”已知该选择“题”的正确答案是CD,且甲?乙?丙?丁四位同学都不会做,下列表述正确的是( )
A. 甲同学仅随机选一个选项,能得2分的概率是
B. 乙同学仅随机选两个选项,能得5分的概率是
C. 丙同学随机选择选项,能得分的概率是
D. 丁同学随机至少选择两个选项,能得分的概率是
【答案】B
8. 已知函数,,若对任意,存在,使,则实数b的取值范围是( )
A. B. C. D.
【答案】C
二?多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9. 已知复数z满足,则下列说法正确的是( )
A. z的共轭复数是 B.
C. z的虚部是 D.
【答案】AB
10. 习近平总书记在党史学习教育动员大会上讲话强调,“要抓好青少年学习教育,着力讲好党的故事?革命的故事?英雄的故事,厚植爱党?爱国?爱社会主义的情感,让红色基因?革命薪火代代传承.”为了深入贯彻习近平总书记的讲话精神,我校积极开展党史学习教育,举行“学党史,颂党恩,跟党走”的主题宣讲.现安排4名教师到高中3个年级进行宣讲,每个年级至少1名教师,则不同的选法有( )
A. B. C. D.
【答案】BD
11. 跑步爱好者小亮为了参加“2021年重庆市第六届运动会半程马拉松”比赛,从2020年1月开始进行长跑训练.他根据某跑步软件记录2020年1月至2020年11月期间每月跑步的里程(单位:十公里)数据整理并绘制了下面的折线图.请根据该折线图分析,下列结论正确的是( )
A. 月跑步里程逐月增加
B. 月跑步里程最小值出现在2月
C. 1月至5月的月跑步里程相对于6月至11月波动性更小
D. 月跑步里程的中位数为5月份对应的里程数
【答案】BCD
12. 已知函数,为的导函数,则下列结论正确的是( )
A. 当时, B. 函数在上只有一个零点
C. 函数在上存在极小值 D. 函数在上存在极大值点
【答案】ABD
三?填空题:本题共4小题,每小题5分,共20分.
13. 在二项式的展开式中,各项系数的和是___________.
【答案】
14. 若,,则___________
【答案】03413
15. 已知函数在处取得极小值,则实数___________.
【答案】
16. 对于三次函数,定义:设为函数的导数,是函数的导数,若方程有实数解,则称点为函数的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现视为条件,已知函数,则它的对称中心为___________;___________.
【答案】 ①. ②.
四?解答题:本题共有6个小题,共70分.解答应写出必要的文字说明?证明过程或演算步骤.
17. 己知的二项展开式中二项式系数之和为512.
(1)求n的值;
(2)求展开式中项的系数.
【答案】(1);(2)
18. 已知函数
(1)求函数单调区间;
(2)求函数在区间上的最大值和最小值.
【答案】(1)增区间:,,减区间:;(2),
19. 新疆是歌舞之乡、瓜果之乡、黄金玉石之邦.在新疆种植棉花有着得天独厚的自然条件,土质呈碱性,夏季温差大,阳光充足,光合作用充分,生长时间长,这种环境下种植的棉花绒长?品质好?产量高,所以新疆棉花举世闻名.当地政府为了更好地向全世界推广宣传新疆棉花,需要大致了解新疆棉花的产量.通过调查发现新疆地区近几年的棉花产量统计如下表:
年份
年份代码
棉花产量 (百万吨)
(1)根据表中数据,建立关于的线性回归方程;
(2)请你根据(1)中的线性回归方程预测今年()新疆棉花的产量.
参考公式:,.
【答案】(1);(2)预测今年()新疆棉花的产量约为万吨.
20. 控烟行动是健康中国重庆行动15项行动之一.2020年9月29日,重庆市五届人大常委会第二十一次会议举行第二次全体会议,表决通过《重庆市公共场所控制吸烟条例》,自2021年1月1日起施行.本条例所称的公共场所,是指公众可以进出的场所或供集体使用的场所,包括餐饮服务场所?住宿休息场所?公众娱乐场所?工作场所?公共交通工具?公用电梯等.为了解重庆某区市民能否自觉遵守该条例,某调查机构借助网络进行了问卷调查,并从参与调查的市民中抽取了200人进行抽样分析,得到如下列联表(单位:人):
能自觉遵守该条例 不能自觉遵守该条例 总计
50岁及以下 90 30 120
50岁以上 50 30 80
总计 140 60 200
(1)根据以上数据,判断是否有90%的把握认为该区市民能否自觉遵守该条例与年龄有关?
(2)将频率视为概率,现从该区50岁及以下的市民中用随机抽样的方法每次抽取1人,共抽取3次.记被抽取的3人中“不能自觉遵守该条例”的人数为X,若每次抽取的结果是相互独立的,求随机变量X的分布列.
附:,其中.
0.15 0.10 0.05 0.025
2.072 2.706 3.841 5.024
【答案】(1)有90%的把握认为该区市民能否自觉遵守该条例与年龄有关(2)答案见解析.
21. 小张?小王两人进行羽毛球比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局小张获胜的概率为,小王获胜的概率为,各局比赛结果相互独立.
(1)求小张在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列和均值.
【答案】(1);(2)分布列见解析,.
22. 已知函数.
(1)若曲线在点处的切线与直线垂直,求m的值:
(2)若对于都有成立,试求m的取值范围;
(3)记,当时,函数在区间上有两个零点,求实数n的取值范围.
【答案】(1);(2);(3).
同课章节目录
