平行四边形的性质
图片预览





文档简介
(共23张PPT)
工厂大门设计
护栏设计
民
间
手
工
制
作
19.1平行四边形(1)
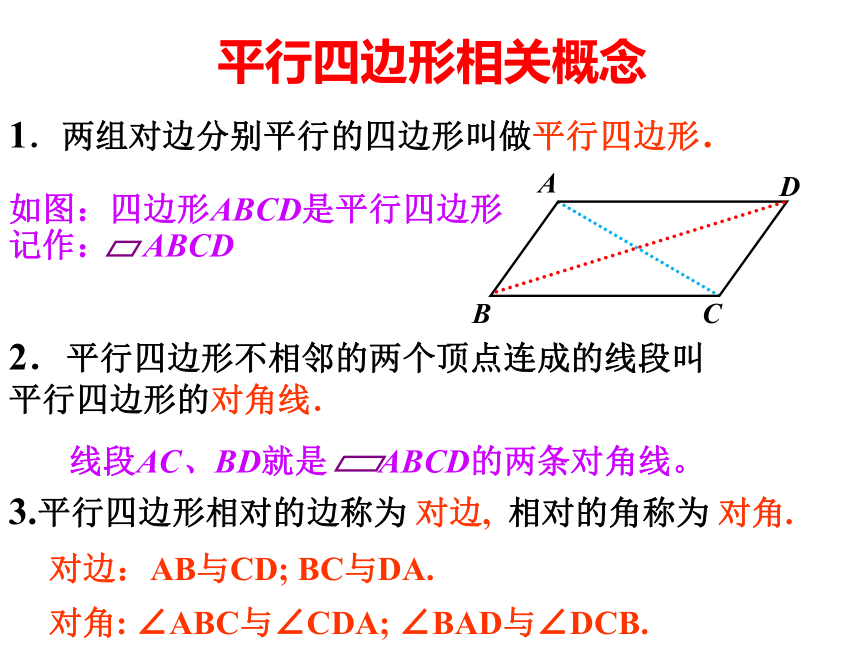
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形记作: ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边, 相对的角称为 对角.
平行四边形相关概念
A
D
C
B
线段AC、BD就是 ABCD的两条对角线。
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
A
B
C
D
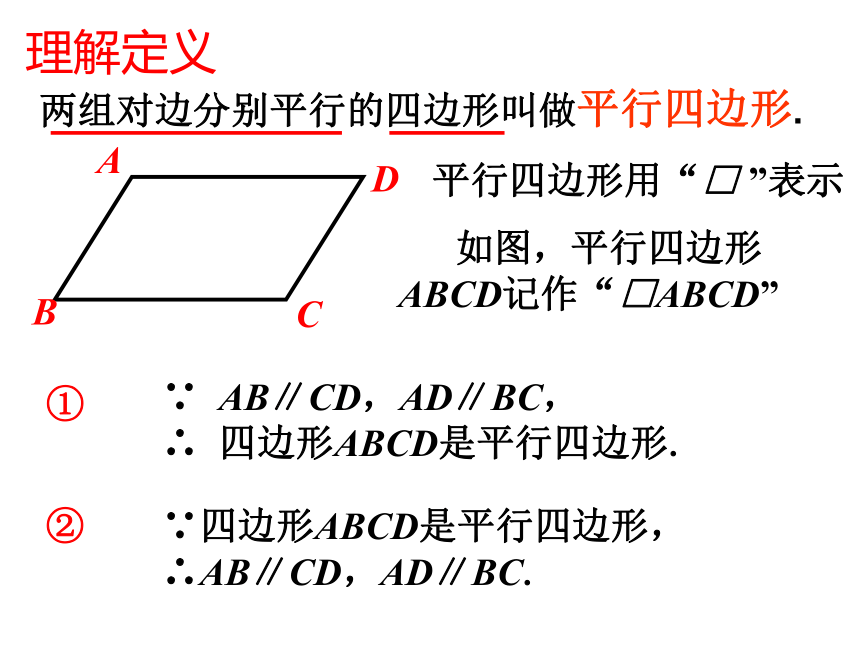
两组对边分别平行的四边形叫做平行四边形.
如图,平行四边形ABCD记作“□ABCD”
①
∵ AB∥CD,AD∥BC,
∴ 四边形ABCD是平行四边形.
②
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
平行四边形用“□ ”表示
理解定义
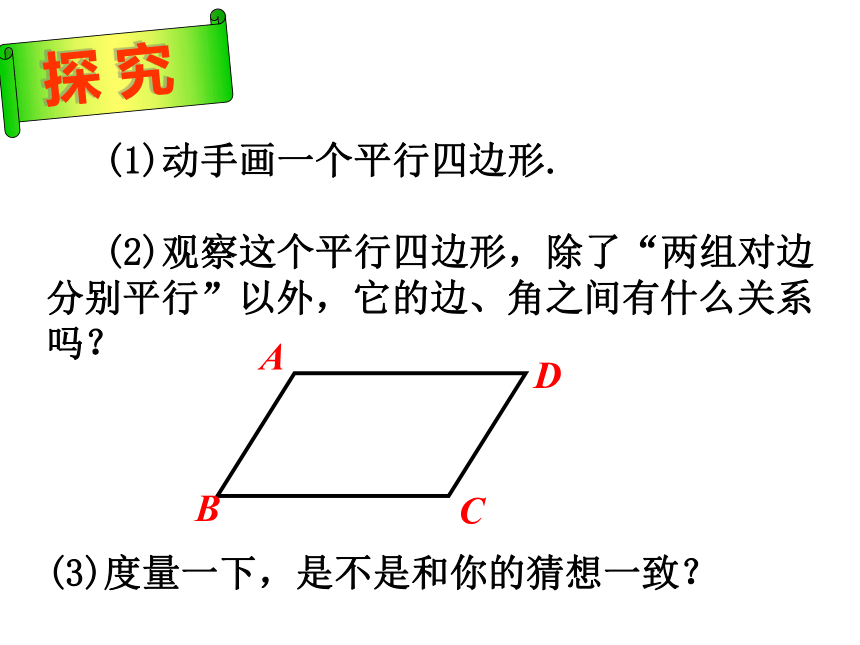
(1)动手画一个平行四边形.
(2)观察这个平行四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?
(3)度量一下,是不是和你的猜想一致?
探 究
A
B
C
D
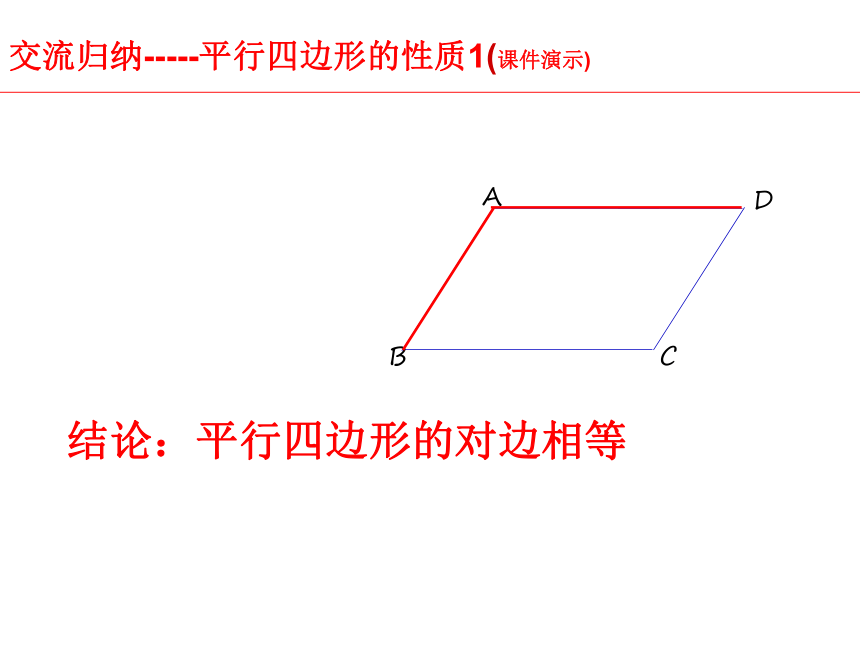
交流归纳-----平行四边形的性质1(课件演示)
C
B
A
D
结论:平行四边形的对边相等
交流归纳-----探索平行四边形的性质2(课件演示)
A
B
C
D
结论:平行四边形的对角相等。
O
前面的结论我们是通过课件演示观察得到的,能否通过数学严谨的逻辑加以证明呢?
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
几何语言:
性质1:平行四边形的对边相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC. (平行四边形的对边相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
性质2:平行四边形的对角相等
1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小结:平行四边形中知道其中两边可求出另外两边的长度;
平行四边形中知道其中一角可求出另外三个角的度数。
1、如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
A
D
B
C
8cm
)
2、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形.
(1)线段AD和BC的长度有什么关系?为什么?
α
(2)若这个四边形的一个外角∠α=38°,这个四边形的每个内角的度数分别是多少 为什么
B
A
C
D
1.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A 6cm B 12cm C 4cm D 8cm
A
B
D
C
A
D
B
C
2.如图,在 ABCD中,∠A:∠B=7:2,求∠C的度数.
E
A
B
D
C
9cm
5cm
3.如图,在 ABCD中,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
4.如图,在平行四边形ABCD中,CE⊥AB,点E为垂足,如果∠A=125°,则∠BCE的度数为多少?
A
D
B
C
E
你在本节课中有哪些收获?
1、平行四边形的定义、符号表示法;
2、平行四边形的性质
平行四边形的对边相等;
平行四边形的对角相等.
3、平行四边形性质的应用
平行四边形的性质是今后证明线段相等和角相等的又一重要依据.
4、在平行四边形性质证明过程中添加辅助线的方法.
活页:第65至66页
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
工厂大门设计
护栏设计
民
间
手
工
制
作
19.1平行四边形(1)
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形记作: ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边, 相对的角称为 对角.
平行四边形相关概念
A
D
C
B
线段AC、BD就是 ABCD的两条对角线。
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
A
B
C
D
两组对边分别平行的四边形叫做平行四边形.
如图,平行四边形ABCD记作“□ABCD”
①
∵ AB∥CD,AD∥BC,
∴ 四边形ABCD是平行四边形.
②
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
平行四边形用“□ ”表示
理解定义
(1)动手画一个平行四边形.
(2)观察这个平行四边形,除了“两组对边分别平行”以外,它的边、角之间有什么关系吗?
(3)度量一下,是不是和你的猜想一致?
探 究
A
B
C
D
交流归纳-----平行四边形的性质1(课件演示)
C
B
A
D
结论:平行四边形的对边相等
交流归纳-----探索平行四边形的性质2(课件演示)
A
B
C
D
结论:平行四边形的对角相等。
O
前面的结论我们是通过课件演示观察得到的,能否通过数学严谨的逻辑加以证明呢?
已知: ABCD
求证:AB=CD,BC=DA;
∠B=∠D,∠A=∠C.
1
2
3
4
即∠BAD=∠DCB
∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC
∴∠1=∠2,∠3=∠4
∠1=∠2
AC=CA
∠3=∠4
∴ △ABC≌△CDA(ASA)
∴AB=CD,BC=DA,
∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
在△ABC和△CDA中
证明:连接AC
几何语言:
性质1:平行四边形的对边相等
∵ 四边形ABCD是平行四边形
∴ AB=CD,AD=BC.(平行四边形的对边相等)
在 ABCD中,
AB=CD,AD=BC. (平行四边形的对边相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
性质2:平行四边形的对角相等
1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小结:平行四边形中知道其中两边可求出另外两边的长度;
平行四边形中知道其中一角可求出另外三个角的度数。
1、如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少
解:∵ 四边形ABCD是平行四边形
∴AB=CD, AD=BC
∵AB=8m
∴CD=8m
又AB+BC+CD+AD=36,
∴ AD=BC=10m
A
D
B
C
8cm
)
2、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形.
(1)线段AD和BC的长度有什么关系?为什么?
α
(2)若这个四边形的一个外角∠α=38°,这个四边形的每个内角的度数分别是多少 为什么
B
A
C
D
1.如图, ABCD的周长是28cm,△ABC的周长是22cm,则AC的长为( )
A 6cm B 12cm C 4cm D 8cm
A
B
D
C
A
D
B
C
2.如图,在 ABCD中,∠A:∠B=7:2,求∠C的度数.
E
A
B
D
C
9cm
5cm
3.如图,在 ABCD中,若BE平分∠ABC,则ED= .
4cm
2
3
5cm
5cm
4cm
1
4.如图,在平行四边形ABCD中,CE⊥AB,点E为垂足,如果∠A=125°,则∠BCE的度数为多少?
A
D
B
C
E
你在本节课中有哪些收获?
1、平行四边形的定义、符号表示法;
2、平行四边形的性质
平行四边形的对边相等;
平行四边形的对角相等.
3、平行四边形性质的应用
平行四边形的性质是今后证明线段相等和角相等的又一重要依据.
4、在平行四边形性质证明过程中添加辅助线的方法.
活页:第65至66页
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
从拼图可以得到什么启示?
小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
