八年级数学下册分式期末复习
图片预览







文档简介
(共82张PPT)
分 式
第十六章
分式方程应用题分类
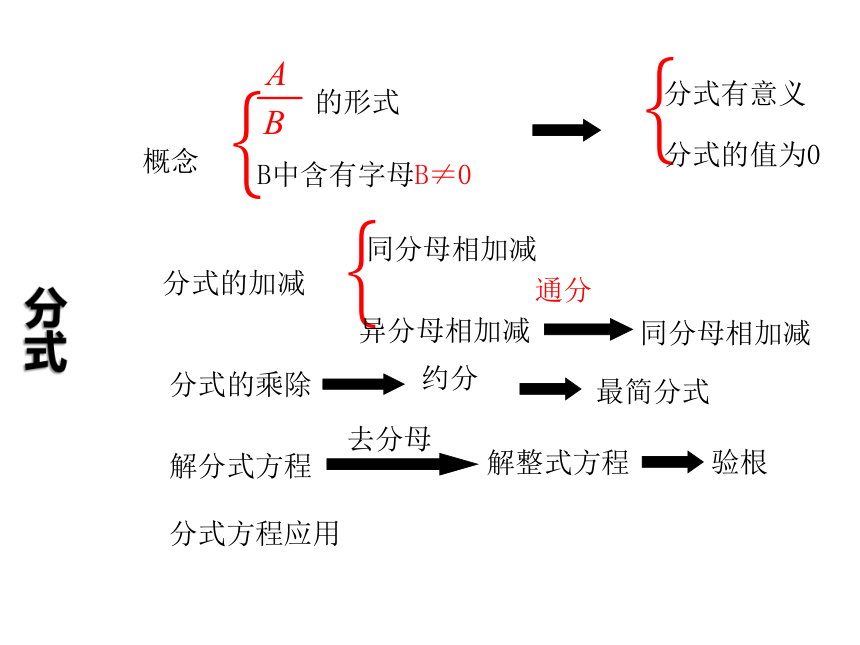
分式
分式有意义
分式的值为0
同分母相加减
异分母相加减
概念
的形式
B中含有字母B≠0
分式的加减
分式的乘除
通分
约分
最简分式
解分式方程
去分母
解整式方程
验根
分式方程应用
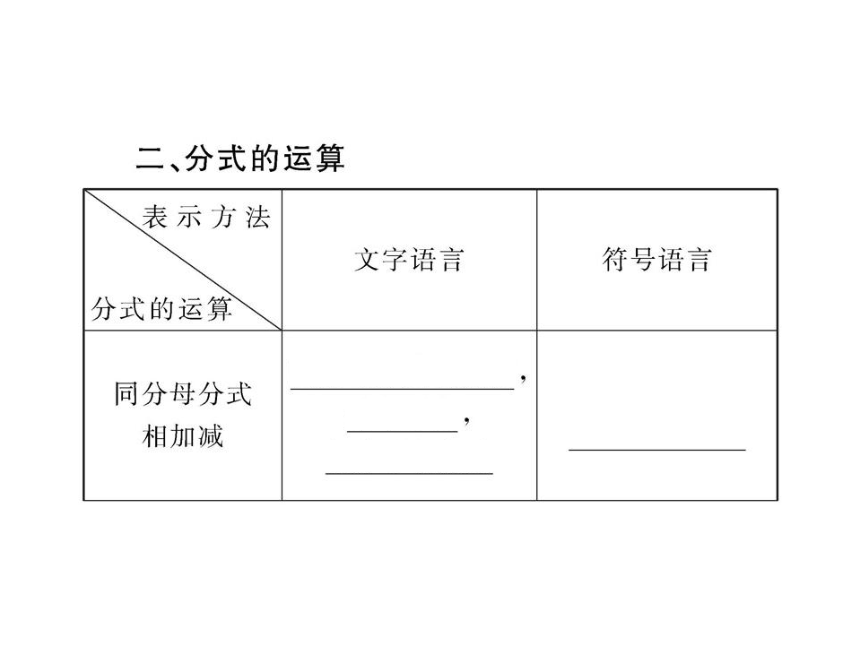
同分母相加减
练习:
:
1.当x取何值时,下列分式有意义
(1)
(2)
(3)
2.当x为何值时,下列分式的值为零:
(1) (2)
3.解下列不等式
(1)
(2)
练习:
:
1.把下列分式的分子、分母的系数化为整数.
(1)
(2)
2.已知: ,求 的值.
3.已知: ,求 的值.
4.若
,求
的值.
5.如果
,试化简
.
练习:
1.计算
(1)
(2)
(3)
(4)
(5)
(6)
(7)
2.先化简后求值
(1)
,其中
满足
(2)已知
,求
的值.
3.已知:
,试求
、
的值.
为何整数时,代数式
4.当
的值是整数,
并求出这个整数值.
技巧性化简
负整数指数幂与科学记数法
某种感冒病毒的直径是0.00000012米,用科学记数法表示为 。
(1)
(2)
(3)
(4)
计算:
(5)
(6)
.
已知
,求(1)
的值;(2)求
的值.
去分母
例.解分式方程:
分析:解分式方程的关键是去分母转化为整式方程
经检验:
是原方程的解,
解:
∴原方程的解为
例题解析
解方程
无解
列分式方程解应用题的一般步骤
1.审:
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
分析题意,找出数量关系和相等关系.
2.设:
选择恰当的未知数,注意单位和语言完整.
3.列:
根据数量和相等关系,正确列出代数式和方程.
4.解:
认真仔细.
5.验:
6.答:
有两次检验.
注意单位和语言完整.且答案要生活化.
(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这
件工作的时间是 小时;
(2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以比原计划
多用天数是 ;
解:设江水每小时的流速是x千米,根据题意得:
2.已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江水每小时的流速是多少千米
试用列表法解例题
例1、A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
分析:(列表)
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
X-30
等量关系:时间相等
思考:这是____问题,三个工作量为____________________
工程
工作量、工作效率、工作时间
解:
等量关系:时间相等
设A种机器人每小时搬运x kg,由题意得
=
解得x=90
经检验x=90是原方程的根
∴ X-30=60
答:A和B两种机器人每小时分别能搬90kg和60kg
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
X-30
例2、八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达。已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度。
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
思考:这是____问题,三个量
为_________________
路程
路程、速度、时间
等量关系:想一想,你觉得是什么呢?
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
解:
设骑车同学的速度为x千米/时,由题意,得
解得x=15
经检验x=15是原方程的根
答:骑车同学的速度为15千米/时
思考,这个等量关系是什么,请写出!还有其他的等量关系吗?你又如何列方程,请试一试!
独立思考完成练习
1、两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作量 工作效率 工作时间
甲队
乙队
思考:这是____问题,总工作量为____
分析:
等量关系:甲队工作量+乙队工作量=1
工程
1
等量关系:甲队工作量+乙队工作量=1
工作量 工作效率 工作时间
甲队
乙队
解:
设乙队单独做需x个月完成工程,由题意,得
解得x=1
经检验x=1是原方程的根
答:乙队施工速度快。
∴乙队单独做1个月完成
∵甲队1个月只做
∴乙队施工速度快
想到解决方法了?
2、从2004年5月起某列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
路程km 速度km/h 时间h
提速前
提速后
思考:这是____问题
行程
等量关系:时间相等
列表分析:
路程km 速度km/h 时间h
提速前
提速后
等量关系:时间相等
解:
设提速前列车的平均速度为x千米/时由题意,得
解得x=
经检验x= 是原方程的根
答:提速前列车的平均速度为 千米/时
1.某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
(1)分别求两年每间出租房屋的租金
(2)求出租房屋的总间数
解法1:设共有x间出租房.
解法2:设第一年每间房屋的租金为x元.
2.某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格
设该市去年用水的价格为x元/吨.
解得 x=1.5
答:该市今年居民用水的价格为2元/吨
1、小明家、王老师家、学校在同一条路上,小明家到王老师家路程为3km,王老师家到学校的路程为0.5km,由于小明的父母战斗在抗“非典”第一线,为了使他能按时到校,王老师每天骑自行车接小明上学,已知王老师骑自行车的速度是步行速度的3倍,每天比平时步行上班多用20分钟,问王老师的步行速度及骑自行车的速度各是多少?
小明家
王老师家
学校
(可以不列表)
2、有一件工程须在规定日期内完成,如果甲队单独施工,则刚好能够完成,如果乙队单独施工,就要超过规定日期3天,现在由甲、乙两队合作施工2天,剩下的工程由乙队单独施工,则刚在规定日期内完成,问规定日期是几天?
1、一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
2、购一年期债券,到期后本利只获2700元,如果债券年利率12.5%,那么利息是多少元
3、骑自行车翻越一个坡地,上坡1千米,下坡1千米,如果上坡的速度是25千米/时,那么下坡要保持什么速度才能使全程的平均速度是30千米/时
4、解一组方程,先用小计算器解20分钟,再改用大计算器解25分钟可解完,如果大计算器的运算速度是小计算器的4倍,并用计算器解这组方程需多少时间
5、甲、乙两列车分别从相距300千米的A、B两站同时相向而行。相遇后,甲车再经过2小时到达B站,乙车再经过4小时30分到达A站,求甲、乙两车的速度。
6、编写一道与下面分式方程相符的实际问题.
一、选择题(每小题6分,共30分)
1.(2010·嘉兴中考)若分式 的值为0,则( )
(A)x=-2 (B)x=-
(C)x= (D)x=2
【解析】选D.3x-6=0且2x+1≠0,解得x=2.
2.若x2-x-2=0,则 的值等于( )
【解析】选A.由x2-x-2=0,得x2-x=2,
所以
3.(2010·绍兴中考)化简 ,可得( )
【解析】选B.
4.计算 的结果是( )
【解析】选B.
5.(2010·黄冈中考)化简:( )·(x-3)的结果是
( )
【解析】选B.( )·(x-3)
二、填空题(每小题6分,共24分)
6.(2010·邵阳中考)化简: =_____.
【解析】
答案:x+y
7.若 =3,则代数式 的值为_____.
【解析】∵ =3,∴ =3,
即x-y=-3xy,
答案:4
8.某市对一段全长1 500米的道路进行改造.原计划每天修x米,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天修路比原计划的2倍还多35米,那么修这条路实际用了_____天.
【解析】由题意知,实际每天修路(2x+35)米,
所以实际用了 天.
答案:
9.已知x2+x-1=0,则
的值等于_____.
【解析】
∵x2+x-1=0,∴-x2=x-1,
∴原式=1.
答案:1
三、解答题(共46分)
10.(10分)(2010·潼南中考)先化简,再求值:(1- )÷
,其中x=2.
【解析】原式
当x=2时, 原式= .
11.(12分)已知x2+3x+1=0,求 的值.
【解析】∵x≠0,x2+3x+1=0两边同除以x,得
x+3+ =0,即x+ =-3.
两边同时平方,得x2+ +2=9,
∴x2+ =7.
同理x4+2+ =49,∴x4+ =47.
12.(12分)(2010·广州中考)已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求 的值.
【解析】∵ax2+bx+1=0(a≠0)有两个相等的实数根,∴Δ=b2-4ac=0 ,即b2-4a=0.
13.(12分)用你发现的规律解答下列问题:
n的代数式表示).
(3)若 的值为 ,求n的值.
【解析】
分 式
第十六章
分式方程应用题分类
分式
分式有意义
分式的值为0
同分母相加减
异分母相加减
概念
的形式
B中含有字母B≠0
分式的加减
分式的乘除
通分
约分
最简分式
解分式方程
去分母
解整式方程
验根
分式方程应用
同分母相加减
练习:
:
1.当x取何值时,下列分式有意义
(1)
(2)
(3)
2.当x为何值时,下列分式的值为零:
(1) (2)
3.解下列不等式
(1)
(2)
练习:
:
1.把下列分式的分子、分母的系数化为整数.
(1)
(2)
2.已知: ,求 的值.
3.已知: ,求 的值.
4.若
,求
的值.
5.如果
,试化简
.
练习:
1.计算
(1)
(2)
(3)
(4)
(5)
(6)
(7)
2.先化简后求值
(1)
,其中
满足
(2)已知
,求
的值.
3.已知:
,试求
、
的值.
为何整数时,代数式
4.当
的值是整数,
并求出这个整数值.
技巧性化简
负整数指数幂与科学记数法
某种感冒病毒的直径是0.00000012米,用科学记数法表示为 。
(1)
(2)
(3)
(4)
计算:
(5)
(6)
.
已知
,求(1)
的值;(2)求
的值.
去分母
例.解分式方程:
分析:解分式方程的关键是去分母转化为整式方程
经检验:
是原方程的解,
解:
∴原方程的解为
例题解析
解方程
无解
列分式方程解应用题的一般步骤
1.审:
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
分析题意,找出数量关系和相等关系.
2.设:
选择恰当的未知数,注意单位和语言完整.
3.列:
根据数量和相等关系,正确列出代数式和方程.
4.解:
认真仔细.
5.验:
6.答:
有两次检验.
注意单位和语言完整.且答案要生活化.
(1)一件工作甲单独做要m小时完成,乙单独做要n小时完成,如果两人合做,完成这
件工作的时间是 小时;
(2)某食堂有米m公斤,原计划每天用粮a公斤,现在每天节约用粮b公斤,则可以比原计划
多用天数是 ;
解:设江水每小时的流速是x千米,根据题意得:
2.已知轮船在静水中每小时行20千米,如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同,那么此江水每小时的流速是多少千米
试用列表法解例题
例1、A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,两种机器人每小时分别搬运多少化工原料?
分析:(列表)
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
X-30
等量关系:时间相等
思考:这是____问题,三个工作量为____________________
工程
工作量、工作效率、工作时间
解:
等量关系:时间相等
设A种机器人每小时搬运x kg,由题意得
=
解得x=90
经检验x=90是原方程的根
∴ X-30=60
答:A和B两种机器人每小时分别能搬90kg和60kg
工作量kg 工作效率kg/h 工作时间h
A
B
900
600
x
X-30
例2、八年级学生去距学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达。已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度。
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
思考:这是____问题,三个量
为_________________
路程
路程、速度、时间
等量关系:想一想,你觉得是什么呢?
路程km 速度km/h 时间h
骑自行车者
乘汽车者
10
10
x
2x
解:
设骑车同学的速度为x千米/时,由题意,得
解得x=15
经检验x=15是原方程的根
答:骑车同学的速度为15千米/时
思考,这个等量关系是什么,请写出!还有其他的等量关系吗?你又如何列方程,请试一试!
独立思考完成练习
1、两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作量 工作效率 工作时间
甲队
乙队
思考:这是____问题,总工作量为____
分析:
等量关系:甲队工作量+乙队工作量=1
工程
1
等量关系:甲队工作量+乙队工作量=1
工作量 工作效率 工作时间
甲队
乙队
解:
设乙队单独做需x个月完成工程,由题意,得
解得x=1
经检验x=1是原方程的根
答:乙队施工速度快。
∴乙队单独做1个月完成
∵甲队1个月只做
∴乙队施工速度快
想到解决方法了?
2、从2004年5月起某列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
路程km 速度km/h 时间h
提速前
提速后
思考:这是____问题
行程
等量关系:时间相等
列表分析:
路程km 速度km/h 时间h
提速前
提速后
等量关系:时间相等
解:
设提速前列车的平均速度为x千米/时由题意,得
解得x=
经检验x= 是原方程的根
答:提速前列车的平均速度为 千米/时
1.某单位将沿街的一部分房屋出租,每间房屋的租金第二年比第一年多500元,所有房屋的租金第一年为9.6万元,第二年为10.2万元.
(1)分别求两年每间出租房屋的租金
(2)求出租房屋的总间数
解法1:设共有x间出租房.
解法2:设第一年每间房屋的租金为x元.
2.某市从今年1月1日起调整居民用水价格,每吨水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5吨,求该市今年居民用水的价格
设该市去年用水的价格为x元/吨.
解得 x=1.5
答:该市今年居民用水的价格为2元/吨
1、小明家、王老师家、学校在同一条路上,小明家到王老师家路程为3km,王老师家到学校的路程为0.5km,由于小明的父母战斗在抗“非典”第一线,为了使他能按时到校,王老师每天骑自行车接小明上学,已知王老师骑自行车的速度是步行速度的3倍,每天比平时步行上班多用20分钟,问王老师的步行速度及骑自行车的速度各是多少?
小明家
王老师家
学校
(可以不列表)
2、有一件工程须在规定日期内完成,如果甲队单独施工,则刚好能够完成,如果乙队单独施工,就要超过规定日期3天,现在由甲、乙两队合作施工2天,剩下的工程由乙队单独施工,则刚在规定日期内完成,问规定日期是几天?
1、一项工程,需要在规定日期内完成,如果甲队独做,恰好如期完成,如果乙队独做,就要超过规定3天,现在由甲、乙两队合作2天,剩下的由乙队独做,也刚好在规定日期内完成,问规定日期是几天?
2、购一年期债券,到期后本利只获2700元,如果债券年利率12.5%,那么利息是多少元
3、骑自行车翻越一个坡地,上坡1千米,下坡1千米,如果上坡的速度是25千米/时,那么下坡要保持什么速度才能使全程的平均速度是30千米/时
4、解一组方程,先用小计算器解20分钟,再改用大计算器解25分钟可解完,如果大计算器的运算速度是小计算器的4倍,并用计算器解这组方程需多少时间
5、甲、乙两列车分别从相距300千米的A、B两站同时相向而行。相遇后,甲车再经过2小时到达B站,乙车再经过4小时30分到达A站,求甲、乙两车的速度。
6、编写一道与下面分式方程相符的实际问题.
一、选择题(每小题6分,共30分)
1.(2010·嘉兴中考)若分式 的值为0,则( )
(A)x=-2 (B)x=-
(C)x= (D)x=2
【解析】选D.3x-6=0且2x+1≠0,解得x=2.
2.若x2-x-2=0,则 的值等于( )
【解析】选A.由x2-x-2=0,得x2-x=2,
所以
3.(2010·绍兴中考)化简 ,可得( )
【解析】选B.
4.计算 的结果是( )
【解析】选B.
5.(2010·黄冈中考)化简:( )·(x-3)的结果是
( )
【解析】选B.( )·(x-3)
二、填空题(每小题6分,共24分)
6.(2010·邵阳中考)化简: =_____.
【解析】
答案:x+y
7.若 =3,则代数式 的值为_____.
【解析】∵ =3,∴ =3,
即x-y=-3xy,
答案:4
8.某市对一段全长1 500米的道路进行改造.原计划每天修x米,为了尽量减少施工对城市交通所造成的影响,实际施工时,每天修路比原计划的2倍还多35米,那么修这条路实际用了_____天.
【解析】由题意知,实际每天修路(2x+35)米,
所以实际用了 天.
答案:
9.已知x2+x-1=0,则
的值等于_____.
【解析】
∵x2+x-1=0,∴-x2=x-1,
∴原式=1.
答案:1
三、解答题(共46分)
10.(10分)(2010·潼南中考)先化简,再求值:(1- )÷
,其中x=2.
【解析】原式
当x=2时, 原式= .
11.(12分)已知x2+3x+1=0,求 的值.
【解析】∵x≠0,x2+3x+1=0两边同除以x,得
x+3+ =0,即x+ =-3.
两边同时平方,得x2+ +2=9,
∴x2+ =7.
同理x4+2+ =49,∴x4+ =47.
12.(12分)(2010·广州中考)已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求 的值.
【解析】∵ax2+bx+1=0(a≠0)有两个相等的实数根,∴Δ=b2-4ac=0 ,即b2-4a=0.
13.(12分)用你发现的规律解答下列问题:
n的代数式表示).
(3)若 的值为 ,求n的值.
【解析】
