1.2.1任意角的三角函数(三) PPT课件
文档属性
| 名称 | 1.2.1任意角的三角函数(三) PPT课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-18 09:47:08 | ||
图片预览









文档简介
(共68张PPT)
1.2.1任意角的
三角函数
复习引入
1. 三角函数的定义
2. 诱导公式
复习引入
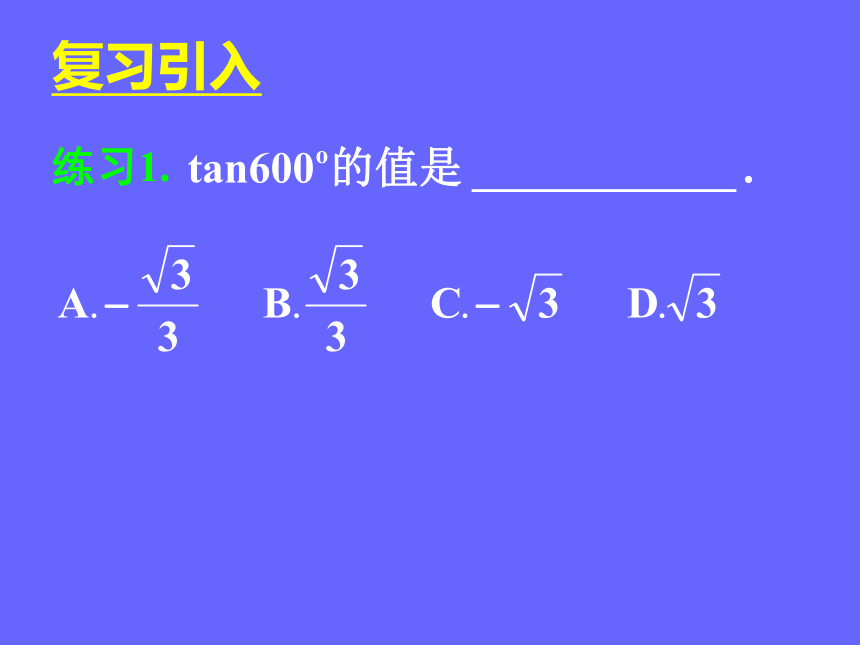
练习1.
复习引入
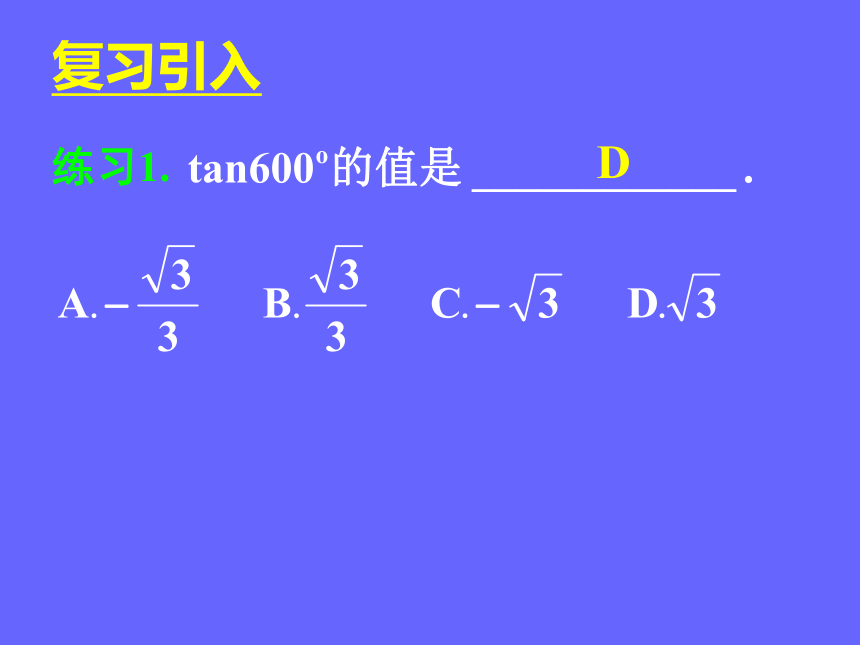
练习1.
D
复习引入
练习2.
复习引入
练习2.
B
复习引入
练习3.
复习引入
练习3.
C
三角函数线
2.有向线段:带有方向(规定了起点和
终点)的线段叫有向线段.
1.单位圆:圆心在原点,半径等于单位
长度的圆叫单位圆.
讲授新课
三角函数线
2.有向线段:带有方向(规定了起点和
终点)的线段叫有向线段.
1.单位圆:圆心在原点,半径等于单位
长度的圆叫单位圆.
本书中的有向线段规定方向与x轴或
y轴的正方向一致的为正值,反之为负值.
讲授新课
练习.说出OM, MO, AT, TA ,
MP, AO的符号.
A(1,0)
O
x
y
M
P
T
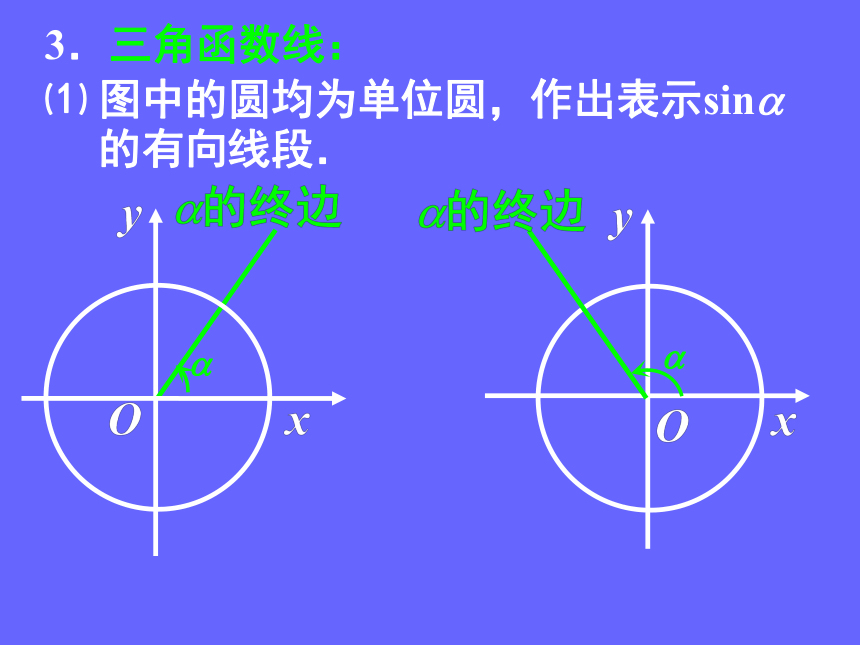
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
从P作x轴垂线,M为垂足,MP为所求.
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
因为sin =y=MP,所以MP叫 的正弦线!
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
从P作x轴垂线,M为垂足,OM为所求.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
因为cos =x=OM,所以OM叫 的余弦线!
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
想一想:
由于tan = ,能否找到使x = 1的点?
想一想:
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
能否找到有向线段使
其大小恰为
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
能否找到有向线段使
其大小恰为
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
能否找到有向线段使
其大小恰为
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
能否找到有向线段使
其大小恰为
AT =
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
即 tan = =AT,
AT是 的正切线.
能否找到有向线段使
其大小恰为
AT =
由于tan = ,能否找到使x = 1的点?
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
过A(1,0)作x轴垂线与终边(或反向延长线)
交于T点,AT为所求.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
因为tan = =AT,所以AT是 的正切线.
把有向线段MP、OM、AT叫做角
的正弦线、余弦线、正切线.
三角函数线
⑶ 过A(1, 0)作x轴垂线与终边(或反向延长
线)交于T.
步骤:
⑴ 找出角的终边与单位圆的交点P.
⑵ 从P点向x轴作垂线,垂足为M.
例1. 作出下列各角的正弦线、余弦线、
正切线.
例2.
例3.
例4.
例5. 利用单位圆写出符合下列条件的角
x的范围.
课堂小结
1. 三角函数线的定义;
2. 会画任意角的三角函数线;
3. 利用单位圆比较三角函数值的大小,
求角的范围.
课后作业
阅读教材P.15-P.17;
《习案》作业四.
1.2.1任意角的
三角函数
复习引入
1. 三角函数的定义
2. 诱导公式
复习引入
练习1.
复习引入
练习1.
D
复习引入
练习2.
复习引入
练习2.
B
复习引入
练习3.
复习引入
练习3.
C
三角函数线
2.有向线段:带有方向(规定了起点和
终点)的线段叫有向线段.
1.单位圆:圆心在原点,半径等于单位
长度的圆叫单位圆.
讲授新课
三角函数线
2.有向线段:带有方向(规定了起点和
终点)的线段叫有向线段.
1.单位圆:圆心在原点,半径等于单位
长度的圆叫单位圆.
本书中的有向线段规定方向与x轴或
y轴的正方向一致的为正值,反之为负值.
讲授新课
练习.说出OM, MO, AT, TA ,
MP, AO的符号.
A(1,0)
O
x
y
M
P
T
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
从P作x轴垂线,M为垂足,MP为所求.
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
因为sin =y=MP,所以MP叫 的正弦线!
⑴ 图中的圆均为单位圆,作出表示sin
的有向线段.
3.三角函数线:
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
从P作x轴垂线,M为垂足,OM为所求.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
因为cos =x=OM,所以OM叫 的余弦线!
⑵图中的圆均为单位圆,作出表示cos 的
有向线段.
想一想:
由于tan = ,能否找到使x = 1的点?
想一想:
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
能否找到有向线段使
其大小恰为
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
能否找到有向线段使
其大小恰为
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
能否找到有向线段使
其大小恰为
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
能否找到有向线段使
其大小恰为
AT =
由于tan = ,能否找到使x = 1的点?
想一想:
过点A(1,0)的切线上的点.
即 tan = =AT,
AT是 的正切线.
能否找到有向线段使
其大小恰为
AT =
由于tan = ,能否找到使x = 1的点?
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
过A(1,0)作x轴垂线与终边(或反向延长线)
交于T点,AT为所求.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
⑶图中的圆均为单位圆,作出表示tan
的有向线段.
因为tan = =AT,所以AT是 的正切线.
把有向线段MP、OM、AT叫做角
的正弦线、余弦线、正切线.
三角函数线
⑶ 过A(1, 0)作x轴垂线与终边(或反向延长
线)交于T.
步骤:
⑴ 找出角的终边与单位圆的交点P.
⑵ 从P点向x轴作垂线,垂足为M.
例1. 作出下列各角的正弦线、余弦线、
正切线.
例2.
例3.
例4.
例5. 利用单位圆写出符合下列条件的角
x的范围.
课堂小结
1. 三角函数线的定义;
2. 会画任意角的三角函数线;
3. 利用单位圆比较三角函数值的大小,
求角的范围.
课后作业
阅读教材P.15-P.17;
《习案》作业四.
