2019-2020学年黑龙江省哈尔滨市道里区七年级(下)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨市道里区七年级(下)期末数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 06:14:58 | ||
图片预览



文档简介
2019-2020学年黑龙江省哈尔滨市道里区七年级(下)期末数学试卷(五四学制)
一、选择题(共10小题).
1.下列选项中的方程,是二元一次方程的是( )
A.x﹣2y=3z B.x=2y C.x2﹣2y=3 D.xy=5
2.下列选项中的图形,有稳定性的是( )
A. B.
C. D.
3.如果a>b,那么下列不等式中不能成立的是( )
A.a﹣3>b﹣3 B.﹣4a<﹣4b C.2a>2b D.﹣5a>﹣5b
4.有两组数据,甲组数据:1,2,3,4,5;乙组数据:2,3,4,5,6;它们的方差分别记为S甲2和S乙2,则
( )
A.S甲2>S乙2 B.S甲2=S乙2 C.S甲2<S乙2 D.无法比较
5.四边形中,如果有一组对角都是直角,那么另一组对角可能( )
A.都是钝角 B.都是锐角
C.一个锐角、一个钝角 D.一个锐角、一个直角
6.为了解某学校七年级学生一次知识问卷的得分情况,小红随机从中抽查50份问卷,结果如表:
知识问卷得分 (单位:分) 65 70 75 80 85
人数 1 15 16 15 3
则这50名同学问卷得分的众数是( )
A.15 B.16 C.75 D.80
7.不等式组的最小整数解是( )
A.﹣2 B.﹣1 C.0 D.1
8.如图,△ABC中∠A=115°,若图中沿虚线剪去∠A,则∠1+∠2等于( )
A.180° B.230° C.290° D.295°
9.如图,CD是直角△ABC斜边AB上的高,CB>CA,图中相等的角共有( )
A.2对 B.3对 C.4对 D.5对
10.在△ABC中,AB=AC,△ABC的中线BD将这个三角形的周长分为9和15两个部分,则BC长为( )
A.12 B.4 C.12或4 D.6或10
二.填空题(每题3分,共30分)
11.已知2x﹣y=4,用含有x的式子表示y,则y= .
12.若点(﹣2,m﹣4)在第二象限,则实数m的范围是 .
13.六边形共有对角线 条.
14.若方程my﹣x=2的一个解是,则m的值为 .
15.十边形的内角和度数是外角和度数的 倍.
16.如图,AD,BE分别为△ABC的高与中线,若BC=8,AD=4,则△BEC的面积为 .
17.若关于x、y的二元一次方程组的解满足x>3﹣y,则a的取值范围是 .
18.如图,AC为四边形ABCD的对角线,∠B=∠D=90°,CD=CB,∠DAC=66°,则∠BCD为 度.
19.四边形ABCD的对角线AC平分∠BAD,CB=CD,∠B=55°,则∠D是 度.
20.如图,△ABC,∠BAC=90°,AD,AE,BF分别为△ABC的中线,高,角平分线,AE与BF交于点G,过点F作BC的垂线,点H为垂足,若AG=12,DH:HC=3:2,则CF的长为 .
三.解答题
21.解下列不等式与方程组.
(1)2x﹣2>4﹣x;
(2).
22.如图,图中网格是由边长为1的小正方形组成的,△ABC的三个顶点都在小正方形的顶点上.
(1)在AC下方确定点D在网格中只画线段AD,CD,使△ADC≌△ABC;
(2)完成(1)后,在网格内确定点E,点E在小正方形的顶点上,画线段EA,ED,使得到的五边形ABCDE的面积是四边形ABCD面积的倍.
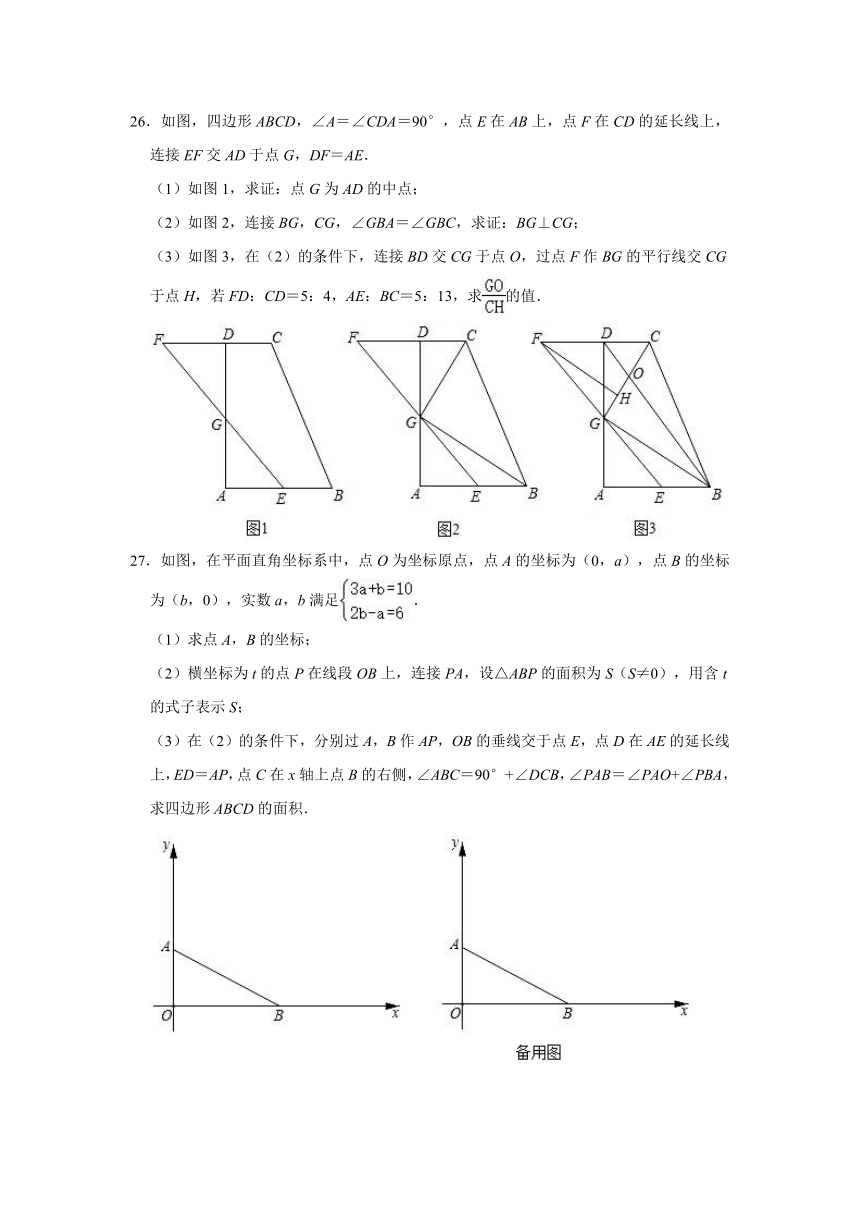
23.某小区为了解2500户居民的月用水情况,从该小区中随机抽取40户进行调查,将得到的数据(取整数)整理后绘制了如图所示的统计图.根据统计图回答下列问题:
(1)求所抽调的40户居民的月用水量的平均数?
(2)直接写出所抽调的40户居民的月用水量的众数及中位数;
(3)估计该小区2500户居民每月共用水多少吨?
24.如图,四边形ABCD的对角线AC,BD交于点O,AD∥BC,OA=OC.
(1)求证:AD=BC;
(2)在不添加任何辅助线的情况下,请直接写出图中所有面积为△AOB面积的2倍的三角形.
25.一汽车销售商店经销AB两种型号轿车.用400万元可购进A型轿车25辆和B型轿车10辆;用300万元可购进A型轿车18辆和B型轿车8辆.
(1)A型与B型轿车每辆的进价分别为多少万元?
(2)若该汽车销售商店购进A,B两种型号的轿车共80辆,且购车资金不超过900万元,该汽车销售商店至少购进A型轿车几辆?
26.如图,四边形ABCD,∠A=∠CDA=90°,点E在AB上,点F在CD的延长线上,连接EF交AD于点G,DF=AE.
(1)如图1,求证:点G为AD的中点;
(2)如图2,连接BG,CG,∠GBA=∠GBC,求证:BG⊥CG;
(3)如图3,在(2)的条件下,连接BD交CG于点O,过点F作BG的平行线交CG于点H,若FD:CD=5:4,AE:BC=5:13,求的值.
27.如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,a),点B的坐标为(b,0),实数a,b满足.
(1)求点A,B的坐标;
(2)横坐标为t的点P在线段OB上,连接PA,设△ABP的面积为S(S≠0),用含t的式子表示S;
(3)在(2)的条件下,分别过A,B作AP,OB的垂线交于点E,点D在AE的延长线上,ED=AP,点C在x轴上点B的右侧,∠ABC=90°+∠DCB,∠PAB=∠PAO+∠PBA,求四边形ABCD的面积.
参考答案
一、选择题(每题3分,共30分)
1.下列选项中的方程,是二元一次方程的是( )
A.x﹣2y=3z B.x=2y C.x2﹣2y=3 D.xy=5
解:A.x﹣2y=3z,是三元一次方程,故本选项不合题意;
B.x=2y属于二元一次方程,故本选项符合题意;
C.x2﹣2y=3,是二元二次方程,故本选项不合题意;
D.xy=5,是二元二次方程,故本选项不合题意;
故选:B.
2.下列选项中的图形,有稳定性的是( )
A. B.
C. D.
解:A、B、D中都是四边形,不具有稳定性,
C中是三角形,有稳定性,
故选:C.
3.如果a>b,那么下列不等式中不能成立的是( )
A.a﹣3>b﹣3 B.﹣4a<﹣4b C.2a>2b D.﹣5a>﹣5b
解:A.a>b两边都减去3得a﹣3>b﹣3,故本选项不符合题意;
B.a>b两边都乘﹣4得﹣4a<﹣4b,故本选项不符合题意;
C.a>b两边都乘2得2a>2b,故本选项不符合题意;
D.a>b两边都乘﹣5得﹣5a<﹣5b,故本选项符合题意.
故选:D.
4.有两组数据,甲组数据:1,2,3,4,5;乙组数据:2,3,4,5,6;它们的方差分别记为S甲2和S乙2,则
( )
A.S甲2>S乙2 B.S甲2=S乙2 C.S甲2<S乙2 D.无法比较
解:甲=(1+2+3+4+5)÷5=3,
乙=(2+3+4+5+6)÷5=4,
∵s甲2=[(3?1)2+(3?2)2+(3?3)2+(3?4)2+(3?5)2]=2,
S乙2=[(4?2)2+(4?3)2+(4?4)2+(4?5)2+(4?6)2]=2,
∴S甲2=S乙2,
故选:B.
5.四边形中,如果有一组对角都是直角,那么另一组对角可能( )
A.都是钝角 B.都是锐角
C.一个锐角、一个钝角 D.一个锐角、一个直角
解:∵四边形的内角和为360°,一组对角都是直角,
∴另一组对角的和为180°,
因此这两个角不可能都是钝角,也不可能都是锐角,也不可能一个锐角一个直角,有可能一个锐角一个钝角,
故选:C.
6.为了解某学校七年级学生一次知识问卷的得分情况,小红随机从中抽查50份问卷,结果如表:
知识问卷得分 (单位:分) 65 70 75 80 85
人数 1 15 16 15 3
则这50名同学问卷得分的众数是( )
A.15 B.16 C.75 D.80
解:数据75出现次数最16,所以众数是75分.
故选:C.
7.不等式组的最小整数解是( )
A.﹣2 B.﹣1 C.0 D.1
解:解不等式2x+3>﹣1,得:x>﹣2,
解不等式x﹣4<2﹣2x,得:x<2,
则不等式组的解集为﹣2<x<2,
所以不等式组的最小整数解为﹣1,
故选:B.
8.如图,△ABC中∠A=115°,若图中沿虚线剪去∠A,则∠1+∠2等于( )
A.180° B.230° C.290° D.295°
解:∵∠A=115°,
∴∠B+∠C=65°,
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣65°=295°.
故选:D.
9.如图,CD是直角△ABC斜边AB上的高,CB>CA,图中相等的角共有( )
A.2对 B.3对 C.4对 D.5对
解:∵CD是直角△ABC斜边AB上的高,
∴∠ACB=∠ADC=∠CDB=90°,
∴∠A+∠ACD=∠ACD+∠DCB=90°,
∴∠A=∠DCB,
同理得:∠B=∠ACD,
∴相等的角一共有5对,
故选:D.
10.在△ABC中,AB=AC,△ABC的中线BD将这个三角形的周长分为9和15两个部分,则BC长为( )
A.12 B.4 C.12或4 D.6或10
解:根据题意,
①当12是腰长与腰长一半时,AC+AC=15,解得AC=10,所以腰长为10;
②当9是腰长与腰长一半时,AC+AC=9,解得AC=6,所以腰长为6.
故腰长等于6或10.
故选:D.
二.填空题(每题3分,共30分)
11.已知2x﹣y=4,用含有x的式子表示y,则y= 2x﹣4 .
解:方程2x﹣y=4,
解得:y=2x﹣4.
故答案为:2x﹣4.
12.若点(﹣2,m﹣4)在第二象限,则实数m的范围是 m>4 .
解:∵点(﹣2,m﹣4)在第二象限,
∴m﹣4>0,
解得,m>4,
故答案为m>4.
13.六边形共有对角线 9 条.
解:根据题意得:,
则六边形共有9条对角线,
故答案为:9.
14.若方程my﹣x=2的一个解是,则m的值为 2 .
解:把代入方程my﹣x=2,
得3m﹣4=2,
解得m=2.
故答案为:2.
15.十边形的内角和度数是外角和度数的 4 倍.
解:∵十边形的内角和为:(10﹣2)×180°=1440°,十边形的外角和为360°,
又∵1440°÷360°=4,
∴十边形的内角和度数是外角和度数的4倍,
故答案为:4.
16.如图,AD,BE分别为△ABC的高与中线,若BC=8,AD=4,则△BEC的面积为 8 .
解:如右图,作BH⊥AC于H,
∴S△ABC=AC?BH,S△BEC=CE?BH,
∵E为AC的中点,
∴CE=AC,
∴S△BEC=S△ABC,
又∵S△ABC=BC?AD==16,
∴S△BEC=S△ABC==8,
故答案为:8.
17.若关于x、y的二元一次方程组的解满足x>3﹣y,则a的取值范围是 a>4 .
解:,
①﹣②×2得:﹣3x=3,即x=﹣1,
把x=﹣1代入②得:﹣2+y=a,即y=2+a,
代入已知不等式得,﹣1>3﹣(2+a),
解得:a>4.
故答案为a>4.
18.如图,AC为四边形ABCD的对角线,∠B=∠D=90°,CD=CB,∠DAC=66°,则∠BCD为 48 度.
解:∵∠B=∠D=90°,
∴△ABC和△ADC是直角三角形,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠DCA=∠BCA,
∵∠DAC=66°,
∴∠DCA=90°﹣∠DAC=24°,
∴∠BCD=∠DCA+∠BCA=2∠DCA=48°,
故答案为:48.
19.四边形ABCD的对角线AC平分∠BAD,CB=CD,∠B=55°,则∠D是 55或125 度.
解:如图1,当∠D为锐角时,
过C作CE⊥AD于E,CF⊥AB于F,
又∵AC平分∠BAD,
∴CE=CF,
在Rt△BCF和Rt△DCE中,
,
∴Rt△BCF≌Rt△DCE(HL),
∴∠D=∠B=55°,
图1
当∠ADC为钝角时,如图2:
图2
过C作CE⊥AD于E,CF⊥AB于F,
又∵AC平分∠BAD,
∴CE=CF,
在Rt△BCF和Rt△DCE中,
,
∴Rt△BCF≌Rt△DCE(HL),
∴∠CDE=∠B=55°,
∴∠ADC=125°,
综上:∠D为55°或125°.
故答案为:55或125.
20.如图,△ABC,∠BAC=90°,AD,AE,BF分别为△ABC的中线,高,角平分线,AE与BF交于点G,过点F作BC的垂线,点H为垂足,若AG=12,DH:HC=3:2,则CF的长为 15 .
解:连接GH,如图所示.
∵∠BAC=90°,FH⊥BC,BF平分∠ABC,
∴AF=HF,∠ABF=∠HBF,
在Rt△ABF和Rt△HBF中,
,
∴Rt△ABF≌Rt△HBF(HL),
∴AB=HB.
在△ABG和△HBG中,
,
∴△ABG≌△HBG(SAS),
∴AG=HG=12,∠BAE=∠BHG,
∵AE⊥BC,
∴∠C+∠CAE=90°,
又∠CAE+∠BAE=90°,
∴∠BAE=∠C,
∴∠C=∠BHG,
∴GH∥AC,
∴△BHG∽△BCF,
∴,
∵DH:HC=3:2,
∴设DH=3x,HC=2x,
∵AD为△ABC的中线,
∴BD=CD=3x+2x=5x,
∴BC=2BD=10x,BH=BD+DH=5x+3x=8x,
∴,
即=,
∴,
∴FC=15,
故答案为:15.
三.解答题
21.解下列不等式与方程组.
(1)2x﹣2>4﹣x;
(2).
解:(1)移项得:2x+x>4+2
合并得:3x>6,
解得:x>2;
(2),
①×2+②得5x=5,即x=1,
将x=1代入②得:y=2,
则方程组的解为.
22.如图,图中网格是由边长为1的小正方形组成的,△ABC的三个顶点都在小正方形的顶点上.
(1)在AC下方确定点D在网格中只画线段AD,CD,使△ADC≌△ABC;
(2)完成(1)后,在网格内确定点E,点E在小正方形的顶点上,画线段EA,ED,使得到的五边形ABCDE的面积是四边形ABCD面积的倍.
解:(1)如图,△ADC即为所求作.
(2)如图,点E即为所求作.
23.某小区为了解2500户居民的月用水情况,从该小区中随机抽取40户进行调查,将得到的数据(取整数)整理后绘制了如图所示的统计图.根据统计图回答下列问题:
(1)求所抽调的40户居民的月用水量的平均数?
(2)直接写出所抽调的40户居民的月用水量的众数及中位数;
(3)估计该小区2500户居民每月共用水多少吨?
解:(1)(6×4+7×12+8×10+9×8+10×6)÷40=8(吨),
答:所抽调的40户居民的月用水量的平均数是8吨;
(2)根据统计图得,所抽调的40户居民的月用水量的众数是7吨,
中位数是第20与第21个数的平均数,
∴中位数是8;
(3)所抽调的40户居民的月用水量的平均数是8吨,
∴该小区2500户居民每月共用水:2500×8=20000(吨),
答:估计该小区2500户居民每月共用水20000吨.
24.如图,四边形ABCD的对角线AC,BD交于点O,AD∥BC,OA=OC.
(1)求证:AD=BC;
(2)在不添加任何辅助线的情况下,请直接写出图中所有面积为△AOB面积的2倍的三角形.
【解答】(1)证明:∵AD∥BC,
∴∠DAO=∠BCO,
在△OAD和△OCB中,
,
∴△OAD≌△OCB(ASA),
∴AD=BC.
(2)解:如图,过点A,C分别作AM⊥DB,CN⊥BD于点M,N,
由(1)知,△OAD≌△OCB,OB=OD,
S△AOB=OB?AM,S△AOD=OD?AM,S△BOC=OB?CN,S△COD=OD?CN,
∵OA=OC,OB=OD,
∴S△AOB=S△BOC=S△AOD=S△COD,
∴S△ABC=S△ACD=S△ABD=S△BCD=2S△AOB,
故面积为△AOB面积的2倍的三角形有:△ABC,△ACD,△ABD,△BCD.
25.一汽车销售商店经销AB两种型号轿车.用400万元可购进A型轿车25辆和B型轿车10辆;用300万元可购进A型轿车18辆和B型轿车8辆.
(1)A型与B型轿车每辆的进价分别为多少万元?
(2)若该汽车销售商店购进A,B两种型号的轿车共80辆,且购车资金不超过900万元,该汽车销售商店至少购进A型轿车几辆?
解:(1)设A型轿车每辆的进价为x万元,B型轿车每辆的进价为y万元,
依题意得:,
解得:.
答:A型轿车每辆的进价为10万元,B型轿车每辆的进价为15万元.
(2)设该汽车销售商店购进A型轿车m辆,则购进B型轿车(80﹣m)辆,
依题意得:10m+15(80﹣m)≤900,
解得:m≥60.
答:该汽车销售商店至少购进A型轿车60辆.
26.如图,四边形ABCD,∠A=∠CDA=90°,点E在AB上,点F在CD的延长线上,连接EF交AD于点G,DF=AE.
(1)如图1,求证:点G为AD的中点;
(2)如图2,连接BG,CG,∠GBA=∠GBC,求证:BG⊥CG;
(3)如图3,在(2)的条件下,连接BD交CG于点O,过点F作BG的平行线交CG于点H,若FD:CD=5:4,AE:BC=5:13,求的值.
解:(1)∵∠A=∠CDA=90°,
∴∠A=∠FDG=90°,
在△FDG和△EAG中,
,
∴△FDG≌△EAG(AAS),
∴DG=AG,
∴点G为AD的中点;
(2)过点G作GM⊥BC于点M,
在△GAB和△GMB中,
,
∴△GAB≌△GMB(AAS),
∴GA=GM,∠AGB=∠MGB=∠AGM,
由(1)知,DG=AG,
∴DG=MG,
在Rt△GDC和Rt△GMC中,
,
∴Rt△GDC≌Rt△GMC(HL),
∴∠DGC=∠MGC=∠DGM,
∵∠AGM+∠DGM=180°,
∴∠CGM+∠BGM=90°,
∴∠CGB=90°,
∴BG⊥CG;
(3)过点G作GM⊥BC于点M,
设AE=DF=5a,则CD=4a,BC=13a,
∴CF=CD+DF=9a,
延长FH交BC于点N,
∵FH∥BG,BG⊥CG,
∴FH⊥CH,
∴∠CHF=∠CHN=90°,
在△FCH和△NCH中,
,
∴△FCH≌△NCH(ASA),
∴CN=CF=9a,
∵DC=CM,AB=GM,
∴BC=GM+CM=AB+CD,
∴AB=9a,
过点C作CK⊥AB于点K,
∴∠AKC=∠DAE=∠CDA=90°,
∴四边形ADCK是矩形,
∴CD=AK=4a,
∴BK=AB﹣AK=5a,
在Rt△BCK中,CK2=BC2﹣BK2,
∴CK=12a,
∴CK=AD=12a,
∴AG=DG=6a,
∵FN∥BG,
∴=,
∴CH=CG,
延长CG交BA延长线于点J,
在△CDG和△JAG中,
,
∴△CDG≌△JAG(ASA),
∴CD=AJ=4a,CG=GJ=CJ,
∴BJ=AB+AJ=13a,
∵∠CDG=∠GAJ=90°,
∴CD∥BJ,
∴==,
∴=
∵CJ=2CG,
∴=,
∴GO=CG﹣CO=CG,
∴==.
27.如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,a),点B的坐标为(b,0),实数a,b满足.
(1)求点A,B的坐标;
(2)横坐标为t的点P在线段OB上,连接PA,设△ABP的面积为S(S≠0),用含t的式子表示S;
(3)在(2)的条件下,分别过A,B作AP,OB的垂线交于点E,点D在AE的延长线上,ED=AP,点C在x轴上点B的右侧,∠ABC=90°+∠DCB,∠PAB=∠PAO+∠PBA,求四边形ABCD的面积.
解:(1)∵.
∴,
∴A(0,2),B(4,0);
(2)∵P(t,0),且0≤t≤4,
∴OP=t,PB=4﹣t,
∴S△ABP=PB?OA=×(4﹣t)×2=4﹣t,
∴S=4﹣t,
∵S≠0,
∴4﹣t≠0,
∴t≠4,
∴0≤t<4,
∴S=4﹣t(0≤t<4);
(3)如图,过点B作BN⊥AP于点N,作BM⊥AE于点M,过点D作DH⊥BC于点H,
∴∠BNP=∠BMA=∠DHB=∠DHC=∠AOB=90°,
∴∠PAO+∠APO=∠PBN+∠BPN=90°,
∵∠APO=∠BPN,
∴∠PAO=∠PBN,
∵∠PAB=∠PAO+∠PBA,∠ABN=∠PBA+∠PBN,
∴∠PAB=∠ABN,
∵∠PAB+∠ABN=90°,
∴∠PAB=∠ABN=45°,
∵∠PAE=90°,
∴∠BAM=45°,
∴△ABM是等腰直角三角形,
∴BM=AM,
在△ABM和△ABN中,
,
∴△ABM≌△ABN(AAS),
∴BM=BN,∠ABM=∠ABN=45°,
∴∠MBN=∠OBE=90°,
∴∠PBN=∠EBM,
在△BPN和△BEM中,
,
∴△BPN≌△BEM(AAS),
∴BP=BE,∠BPN=∠BEM,
∵∠BPA=180°﹣∠BPN,∠BED=180°﹣∠BEM,
∴∠BPA=∠BED,
在△BAP和△BDE中,
,
∴△BAP≌△BDE(SAS),
∴∠ABP=∠DBE,BA=BD,
∵DH∥BE,
∴∠BDH=∠DBE,
∴∠BDH=∠ABP,
在△BDH和△ABO中,
,
∴△BDH≌△ABO(AAS),
∴∠DBH=∠BAO,DH=OB=4,BH=OA=2,
∴OH=OB+BH=4+2=6,
∵∠ABC=90°+∠DCB,∠ABC=90°+∠ABE,
∴∠DCB=∠ABE,
∵BE∥OA,
∴∠ABE=∠BAO,
∴∠DCB=∠DBH,
在△DCH和△DBH中,
,
∴△DCH≌△DBH(AAS),
∴△DCH≌△BAO,
∴S四边形ABCD=S四边形ABHD+S△DCH=S四边形ABHD+S△BAO=S四边形AOHD,
∵S四边形AOHD=×(OA+DH)×OH=×(2+4)×6=18,
∴S四边形ABCD=18.
一、选择题(共10小题).
1.下列选项中的方程,是二元一次方程的是( )
A.x﹣2y=3z B.x=2y C.x2﹣2y=3 D.xy=5
2.下列选项中的图形,有稳定性的是( )
A. B.
C. D.
3.如果a>b,那么下列不等式中不能成立的是( )
A.a﹣3>b﹣3 B.﹣4a<﹣4b C.2a>2b D.﹣5a>﹣5b
4.有两组数据,甲组数据:1,2,3,4,5;乙组数据:2,3,4,5,6;它们的方差分别记为S甲2和S乙2,则
( )
A.S甲2>S乙2 B.S甲2=S乙2 C.S甲2<S乙2 D.无法比较
5.四边形中,如果有一组对角都是直角,那么另一组对角可能( )
A.都是钝角 B.都是锐角
C.一个锐角、一个钝角 D.一个锐角、一个直角
6.为了解某学校七年级学生一次知识问卷的得分情况,小红随机从中抽查50份问卷,结果如表:
知识问卷得分 (单位:分) 65 70 75 80 85
人数 1 15 16 15 3
则这50名同学问卷得分的众数是( )
A.15 B.16 C.75 D.80
7.不等式组的最小整数解是( )
A.﹣2 B.﹣1 C.0 D.1
8.如图,△ABC中∠A=115°,若图中沿虚线剪去∠A,则∠1+∠2等于( )
A.180° B.230° C.290° D.295°
9.如图,CD是直角△ABC斜边AB上的高,CB>CA,图中相等的角共有( )
A.2对 B.3对 C.4对 D.5对
10.在△ABC中,AB=AC,△ABC的中线BD将这个三角形的周长分为9和15两个部分,则BC长为( )
A.12 B.4 C.12或4 D.6或10
二.填空题(每题3分,共30分)
11.已知2x﹣y=4,用含有x的式子表示y,则y= .
12.若点(﹣2,m﹣4)在第二象限,则实数m的范围是 .
13.六边形共有对角线 条.
14.若方程my﹣x=2的一个解是,则m的值为 .
15.十边形的内角和度数是外角和度数的 倍.
16.如图,AD,BE分别为△ABC的高与中线,若BC=8,AD=4,则△BEC的面积为 .
17.若关于x、y的二元一次方程组的解满足x>3﹣y,则a的取值范围是 .
18.如图,AC为四边形ABCD的对角线,∠B=∠D=90°,CD=CB,∠DAC=66°,则∠BCD为 度.
19.四边形ABCD的对角线AC平分∠BAD,CB=CD,∠B=55°,则∠D是 度.
20.如图,△ABC,∠BAC=90°,AD,AE,BF分别为△ABC的中线,高,角平分线,AE与BF交于点G,过点F作BC的垂线,点H为垂足,若AG=12,DH:HC=3:2,则CF的长为 .
三.解答题
21.解下列不等式与方程组.
(1)2x﹣2>4﹣x;
(2).
22.如图,图中网格是由边长为1的小正方形组成的,△ABC的三个顶点都在小正方形的顶点上.
(1)在AC下方确定点D在网格中只画线段AD,CD,使△ADC≌△ABC;
(2)完成(1)后,在网格内确定点E,点E在小正方形的顶点上,画线段EA,ED,使得到的五边形ABCDE的面积是四边形ABCD面积的倍.
23.某小区为了解2500户居民的月用水情况,从该小区中随机抽取40户进行调查,将得到的数据(取整数)整理后绘制了如图所示的统计图.根据统计图回答下列问题:
(1)求所抽调的40户居民的月用水量的平均数?
(2)直接写出所抽调的40户居民的月用水量的众数及中位数;
(3)估计该小区2500户居民每月共用水多少吨?
24.如图,四边形ABCD的对角线AC,BD交于点O,AD∥BC,OA=OC.
(1)求证:AD=BC;
(2)在不添加任何辅助线的情况下,请直接写出图中所有面积为△AOB面积的2倍的三角形.
25.一汽车销售商店经销AB两种型号轿车.用400万元可购进A型轿车25辆和B型轿车10辆;用300万元可购进A型轿车18辆和B型轿车8辆.
(1)A型与B型轿车每辆的进价分别为多少万元?
(2)若该汽车销售商店购进A,B两种型号的轿车共80辆,且购车资金不超过900万元,该汽车销售商店至少购进A型轿车几辆?
26.如图,四边形ABCD,∠A=∠CDA=90°,点E在AB上,点F在CD的延长线上,连接EF交AD于点G,DF=AE.
(1)如图1,求证:点G为AD的中点;
(2)如图2,连接BG,CG,∠GBA=∠GBC,求证:BG⊥CG;
(3)如图3,在(2)的条件下,连接BD交CG于点O,过点F作BG的平行线交CG于点H,若FD:CD=5:4,AE:BC=5:13,求的值.
27.如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,a),点B的坐标为(b,0),实数a,b满足.
(1)求点A,B的坐标;
(2)横坐标为t的点P在线段OB上,连接PA,设△ABP的面积为S(S≠0),用含t的式子表示S;
(3)在(2)的条件下,分别过A,B作AP,OB的垂线交于点E,点D在AE的延长线上,ED=AP,点C在x轴上点B的右侧,∠ABC=90°+∠DCB,∠PAB=∠PAO+∠PBA,求四边形ABCD的面积.
参考答案
一、选择题(每题3分,共30分)
1.下列选项中的方程,是二元一次方程的是( )
A.x﹣2y=3z B.x=2y C.x2﹣2y=3 D.xy=5
解:A.x﹣2y=3z,是三元一次方程,故本选项不合题意;
B.x=2y属于二元一次方程,故本选项符合题意;
C.x2﹣2y=3,是二元二次方程,故本选项不合题意;
D.xy=5,是二元二次方程,故本选项不合题意;
故选:B.
2.下列选项中的图形,有稳定性的是( )
A. B.
C. D.
解:A、B、D中都是四边形,不具有稳定性,
C中是三角形,有稳定性,
故选:C.
3.如果a>b,那么下列不等式中不能成立的是( )
A.a﹣3>b﹣3 B.﹣4a<﹣4b C.2a>2b D.﹣5a>﹣5b
解:A.a>b两边都减去3得a﹣3>b﹣3,故本选项不符合题意;
B.a>b两边都乘﹣4得﹣4a<﹣4b,故本选项不符合题意;
C.a>b两边都乘2得2a>2b,故本选项不符合题意;
D.a>b两边都乘﹣5得﹣5a<﹣5b,故本选项符合题意.
故选:D.
4.有两组数据,甲组数据:1,2,3,4,5;乙组数据:2,3,4,5,6;它们的方差分别记为S甲2和S乙2,则
( )
A.S甲2>S乙2 B.S甲2=S乙2 C.S甲2<S乙2 D.无法比较
解:甲=(1+2+3+4+5)÷5=3,
乙=(2+3+4+5+6)÷5=4,
∵s甲2=[(3?1)2+(3?2)2+(3?3)2+(3?4)2+(3?5)2]=2,
S乙2=[(4?2)2+(4?3)2+(4?4)2+(4?5)2+(4?6)2]=2,
∴S甲2=S乙2,
故选:B.
5.四边形中,如果有一组对角都是直角,那么另一组对角可能( )
A.都是钝角 B.都是锐角
C.一个锐角、一个钝角 D.一个锐角、一个直角
解:∵四边形的内角和为360°,一组对角都是直角,
∴另一组对角的和为180°,
因此这两个角不可能都是钝角,也不可能都是锐角,也不可能一个锐角一个直角,有可能一个锐角一个钝角,
故选:C.
6.为了解某学校七年级学生一次知识问卷的得分情况,小红随机从中抽查50份问卷,结果如表:
知识问卷得分 (单位:分) 65 70 75 80 85
人数 1 15 16 15 3
则这50名同学问卷得分的众数是( )
A.15 B.16 C.75 D.80
解:数据75出现次数最16,所以众数是75分.
故选:C.
7.不等式组的最小整数解是( )
A.﹣2 B.﹣1 C.0 D.1
解:解不等式2x+3>﹣1,得:x>﹣2,
解不等式x﹣4<2﹣2x,得:x<2,
则不等式组的解集为﹣2<x<2,
所以不等式组的最小整数解为﹣1,
故选:B.
8.如图,△ABC中∠A=115°,若图中沿虚线剪去∠A,则∠1+∠2等于( )
A.180° B.230° C.290° D.295°
解:∵∠A=115°,
∴∠B+∠C=65°,
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣65°=295°.
故选:D.
9.如图,CD是直角△ABC斜边AB上的高,CB>CA,图中相等的角共有( )
A.2对 B.3对 C.4对 D.5对
解:∵CD是直角△ABC斜边AB上的高,
∴∠ACB=∠ADC=∠CDB=90°,
∴∠A+∠ACD=∠ACD+∠DCB=90°,
∴∠A=∠DCB,
同理得:∠B=∠ACD,
∴相等的角一共有5对,
故选:D.
10.在△ABC中,AB=AC,△ABC的中线BD将这个三角形的周长分为9和15两个部分,则BC长为( )
A.12 B.4 C.12或4 D.6或10
解:根据题意,
①当12是腰长与腰长一半时,AC+AC=15,解得AC=10,所以腰长为10;
②当9是腰长与腰长一半时,AC+AC=9,解得AC=6,所以腰长为6.
故腰长等于6或10.
故选:D.
二.填空题(每题3分,共30分)
11.已知2x﹣y=4,用含有x的式子表示y,则y= 2x﹣4 .
解:方程2x﹣y=4,
解得:y=2x﹣4.
故答案为:2x﹣4.
12.若点(﹣2,m﹣4)在第二象限,则实数m的范围是 m>4 .
解:∵点(﹣2,m﹣4)在第二象限,
∴m﹣4>0,
解得,m>4,
故答案为m>4.
13.六边形共有对角线 9 条.
解:根据题意得:,
则六边形共有9条对角线,
故答案为:9.
14.若方程my﹣x=2的一个解是,则m的值为 2 .
解:把代入方程my﹣x=2,
得3m﹣4=2,
解得m=2.
故答案为:2.
15.十边形的内角和度数是外角和度数的 4 倍.
解:∵十边形的内角和为:(10﹣2)×180°=1440°,十边形的外角和为360°,
又∵1440°÷360°=4,
∴十边形的内角和度数是外角和度数的4倍,
故答案为:4.
16.如图,AD,BE分别为△ABC的高与中线,若BC=8,AD=4,则△BEC的面积为 8 .
解:如右图,作BH⊥AC于H,
∴S△ABC=AC?BH,S△BEC=CE?BH,
∵E为AC的中点,
∴CE=AC,
∴S△BEC=S△ABC,
又∵S△ABC=BC?AD==16,
∴S△BEC=S△ABC==8,
故答案为:8.
17.若关于x、y的二元一次方程组的解满足x>3﹣y,则a的取值范围是 a>4 .
解:,
①﹣②×2得:﹣3x=3,即x=﹣1,
把x=﹣1代入②得:﹣2+y=a,即y=2+a,
代入已知不等式得,﹣1>3﹣(2+a),
解得:a>4.
故答案为a>4.
18.如图,AC为四边形ABCD的对角线,∠B=∠D=90°,CD=CB,∠DAC=66°,则∠BCD为 48 度.
解:∵∠B=∠D=90°,
∴△ABC和△ADC是直角三角形,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠DCA=∠BCA,
∵∠DAC=66°,
∴∠DCA=90°﹣∠DAC=24°,
∴∠BCD=∠DCA+∠BCA=2∠DCA=48°,
故答案为:48.
19.四边形ABCD的对角线AC平分∠BAD,CB=CD,∠B=55°,则∠D是 55或125 度.
解:如图1,当∠D为锐角时,
过C作CE⊥AD于E,CF⊥AB于F,
又∵AC平分∠BAD,
∴CE=CF,
在Rt△BCF和Rt△DCE中,
,
∴Rt△BCF≌Rt△DCE(HL),
∴∠D=∠B=55°,
图1
当∠ADC为钝角时,如图2:
图2
过C作CE⊥AD于E,CF⊥AB于F,
又∵AC平分∠BAD,
∴CE=CF,
在Rt△BCF和Rt△DCE中,
,
∴Rt△BCF≌Rt△DCE(HL),
∴∠CDE=∠B=55°,
∴∠ADC=125°,
综上:∠D为55°或125°.
故答案为:55或125.
20.如图,△ABC,∠BAC=90°,AD,AE,BF分别为△ABC的中线,高,角平分线,AE与BF交于点G,过点F作BC的垂线,点H为垂足,若AG=12,DH:HC=3:2,则CF的长为 15 .
解:连接GH,如图所示.
∵∠BAC=90°,FH⊥BC,BF平分∠ABC,
∴AF=HF,∠ABF=∠HBF,
在Rt△ABF和Rt△HBF中,
,
∴Rt△ABF≌Rt△HBF(HL),
∴AB=HB.
在△ABG和△HBG中,
,
∴△ABG≌△HBG(SAS),
∴AG=HG=12,∠BAE=∠BHG,
∵AE⊥BC,
∴∠C+∠CAE=90°,
又∠CAE+∠BAE=90°,
∴∠BAE=∠C,
∴∠C=∠BHG,
∴GH∥AC,
∴△BHG∽△BCF,
∴,
∵DH:HC=3:2,
∴设DH=3x,HC=2x,
∵AD为△ABC的中线,
∴BD=CD=3x+2x=5x,
∴BC=2BD=10x,BH=BD+DH=5x+3x=8x,
∴,
即=,
∴,
∴FC=15,
故答案为:15.
三.解答题
21.解下列不等式与方程组.
(1)2x﹣2>4﹣x;
(2).
解:(1)移项得:2x+x>4+2
合并得:3x>6,
解得:x>2;
(2),
①×2+②得5x=5,即x=1,
将x=1代入②得:y=2,
则方程组的解为.
22.如图,图中网格是由边长为1的小正方形组成的,△ABC的三个顶点都在小正方形的顶点上.
(1)在AC下方确定点D在网格中只画线段AD,CD,使△ADC≌△ABC;
(2)完成(1)后,在网格内确定点E,点E在小正方形的顶点上,画线段EA,ED,使得到的五边形ABCDE的面积是四边形ABCD面积的倍.
解:(1)如图,△ADC即为所求作.
(2)如图,点E即为所求作.
23.某小区为了解2500户居民的月用水情况,从该小区中随机抽取40户进行调查,将得到的数据(取整数)整理后绘制了如图所示的统计图.根据统计图回答下列问题:
(1)求所抽调的40户居民的月用水量的平均数?
(2)直接写出所抽调的40户居民的月用水量的众数及中位数;
(3)估计该小区2500户居民每月共用水多少吨?
解:(1)(6×4+7×12+8×10+9×8+10×6)÷40=8(吨),
答:所抽调的40户居民的月用水量的平均数是8吨;
(2)根据统计图得,所抽调的40户居民的月用水量的众数是7吨,
中位数是第20与第21个数的平均数,
∴中位数是8;
(3)所抽调的40户居民的月用水量的平均数是8吨,
∴该小区2500户居民每月共用水:2500×8=20000(吨),
答:估计该小区2500户居民每月共用水20000吨.
24.如图,四边形ABCD的对角线AC,BD交于点O,AD∥BC,OA=OC.
(1)求证:AD=BC;
(2)在不添加任何辅助线的情况下,请直接写出图中所有面积为△AOB面积的2倍的三角形.
【解答】(1)证明:∵AD∥BC,
∴∠DAO=∠BCO,
在△OAD和△OCB中,
,
∴△OAD≌△OCB(ASA),
∴AD=BC.
(2)解:如图,过点A,C分别作AM⊥DB,CN⊥BD于点M,N,
由(1)知,△OAD≌△OCB,OB=OD,
S△AOB=OB?AM,S△AOD=OD?AM,S△BOC=OB?CN,S△COD=OD?CN,
∵OA=OC,OB=OD,
∴S△AOB=S△BOC=S△AOD=S△COD,
∴S△ABC=S△ACD=S△ABD=S△BCD=2S△AOB,
故面积为△AOB面积的2倍的三角形有:△ABC,△ACD,△ABD,△BCD.
25.一汽车销售商店经销AB两种型号轿车.用400万元可购进A型轿车25辆和B型轿车10辆;用300万元可购进A型轿车18辆和B型轿车8辆.
(1)A型与B型轿车每辆的进价分别为多少万元?
(2)若该汽车销售商店购进A,B两种型号的轿车共80辆,且购车资金不超过900万元,该汽车销售商店至少购进A型轿车几辆?
解:(1)设A型轿车每辆的进价为x万元,B型轿车每辆的进价为y万元,
依题意得:,
解得:.
答:A型轿车每辆的进价为10万元,B型轿车每辆的进价为15万元.
(2)设该汽车销售商店购进A型轿车m辆,则购进B型轿车(80﹣m)辆,
依题意得:10m+15(80﹣m)≤900,
解得:m≥60.
答:该汽车销售商店至少购进A型轿车60辆.
26.如图,四边形ABCD,∠A=∠CDA=90°,点E在AB上,点F在CD的延长线上,连接EF交AD于点G,DF=AE.
(1)如图1,求证:点G为AD的中点;
(2)如图2,连接BG,CG,∠GBA=∠GBC,求证:BG⊥CG;
(3)如图3,在(2)的条件下,连接BD交CG于点O,过点F作BG的平行线交CG于点H,若FD:CD=5:4,AE:BC=5:13,求的值.
解:(1)∵∠A=∠CDA=90°,
∴∠A=∠FDG=90°,
在△FDG和△EAG中,
,
∴△FDG≌△EAG(AAS),
∴DG=AG,
∴点G为AD的中点;
(2)过点G作GM⊥BC于点M,
在△GAB和△GMB中,
,
∴△GAB≌△GMB(AAS),
∴GA=GM,∠AGB=∠MGB=∠AGM,
由(1)知,DG=AG,
∴DG=MG,
在Rt△GDC和Rt△GMC中,
,
∴Rt△GDC≌Rt△GMC(HL),
∴∠DGC=∠MGC=∠DGM,
∵∠AGM+∠DGM=180°,
∴∠CGM+∠BGM=90°,
∴∠CGB=90°,
∴BG⊥CG;
(3)过点G作GM⊥BC于点M,
设AE=DF=5a,则CD=4a,BC=13a,
∴CF=CD+DF=9a,
延长FH交BC于点N,
∵FH∥BG,BG⊥CG,
∴FH⊥CH,
∴∠CHF=∠CHN=90°,
在△FCH和△NCH中,
,
∴△FCH≌△NCH(ASA),
∴CN=CF=9a,
∵DC=CM,AB=GM,
∴BC=GM+CM=AB+CD,
∴AB=9a,
过点C作CK⊥AB于点K,
∴∠AKC=∠DAE=∠CDA=90°,
∴四边形ADCK是矩形,
∴CD=AK=4a,
∴BK=AB﹣AK=5a,
在Rt△BCK中,CK2=BC2﹣BK2,
∴CK=12a,
∴CK=AD=12a,
∴AG=DG=6a,
∵FN∥BG,
∴=,
∴CH=CG,
延长CG交BA延长线于点J,
在△CDG和△JAG中,
,
∴△CDG≌△JAG(ASA),
∴CD=AJ=4a,CG=GJ=CJ,
∴BJ=AB+AJ=13a,
∵∠CDG=∠GAJ=90°,
∴CD∥BJ,
∴==,
∴=
∵CJ=2CG,
∴=,
∴GO=CG﹣CO=CG,
∴==.
27.如图,在平面直角坐标系中,点O为坐标原点,点A的坐标为(0,a),点B的坐标为(b,0),实数a,b满足.
(1)求点A,B的坐标;
(2)横坐标为t的点P在线段OB上,连接PA,设△ABP的面积为S(S≠0),用含t的式子表示S;
(3)在(2)的条件下,分别过A,B作AP,OB的垂线交于点E,点D在AE的延长线上,ED=AP,点C在x轴上点B的右侧,∠ABC=90°+∠DCB,∠PAB=∠PAO+∠PBA,求四边形ABCD的面积.
解:(1)∵.
∴,
∴A(0,2),B(4,0);
(2)∵P(t,0),且0≤t≤4,
∴OP=t,PB=4﹣t,
∴S△ABP=PB?OA=×(4﹣t)×2=4﹣t,
∴S=4﹣t,
∵S≠0,
∴4﹣t≠0,
∴t≠4,
∴0≤t<4,
∴S=4﹣t(0≤t<4);
(3)如图,过点B作BN⊥AP于点N,作BM⊥AE于点M,过点D作DH⊥BC于点H,
∴∠BNP=∠BMA=∠DHB=∠DHC=∠AOB=90°,
∴∠PAO+∠APO=∠PBN+∠BPN=90°,
∵∠APO=∠BPN,
∴∠PAO=∠PBN,
∵∠PAB=∠PAO+∠PBA,∠ABN=∠PBA+∠PBN,
∴∠PAB=∠ABN,
∵∠PAB+∠ABN=90°,
∴∠PAB=∠ABN=45°,
∵∠PAE=90°,
∴∠BAM=45°,
∴△ABM是等腰直角三角形,
∴BM=AM,
在△ABM和△ABN中,
,
∴△ABM≌△ABN(AAS),
∴BM=BN,∠ABM=∠ABN=45°,
∴∠MBN=∠OBE=90°,
∴∠PBN=∠EBM,
在△BPN和△BEM中,
,
∴△BPN≌△BEM(AAS),
∴BP=BE,∠BPN=∠BEM,
∵∠BPA=180°﹣∠BPN,∠BED=180°﹣∠BEM,
∴∠BPA=∠BED,
在△BAP和△BDE中,
,
∴△BAP≌△BDE(SAS),
∴∠ABP=∠DBE,BA=BD,
∵DH∥BE,
∴∠BDH=∠DBE,
∴∠BDH=∠ABP,
在△BDH和△ABO中,
,
∴△BDH≌△ABO(AAS),
∴∠DBH=∠BAO,DH=OB=4,BH=OA=2,
∴OH=OB+BH=4+2=6,
∵∠ABC=90°+∠DCB,∠ABC=90°+∠ABE,
∴∠DCB=∠ABE,
∵BE∥OA,
∴∠ABE=∠BAO,
∴∠DCB=∠DBH,
在△DCH和△DBH中,
,
∴△DCH≌△DBH(AAS),
∴△DCH≌△BAO,
∴S四边形ABCD=S四边形ABHD+S△DCH=S四边形ABHD+S△BAO=S四边形AOHD,
∵S四边形AOHD=×(OA+DH)×OH=×(2+4)×6=18,
∴S四边形ABCD=18.
同课章节目录
