人教版八年级数学上册 12.1全等三角形 同步练习(Word版,有答案)
文档属性
| 名称 | 人教版八年级数学上册 12.1全等三角形 同步练习(Word版,有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 00:00:00 | ||
图片预览


文档简介
12.1全等三角形
一、单选题
1.下列图形中,属于全等图形的是( )
A.
B.
C.
D.
2.全等三角形是(
)
A.面积相等的三角形
B.角相等的三角形
C.周长相等的三角形
D.完全重合的三角形
3.下列说法:两个形状相同的图形称为全等图形;两个正方形是全等图形;全等图形的形状、大小都相同;面积相等的两个三角形是全等图形其中,正确的是(????)
A.
B.
C.
D.
4.如图,,,,则的度数为(
)
A.20°
B.25°
C.30°
D.35°
5.如图,下面4个正方形的边长都相等,其中阴影部分的面积相等的图形有(
)
A.0个
B.2个
C.3个
D.4个
6.如图,△ABE≌△ACD,BC=10,DE=4,则DC的长是( )
A.8
B.7
C.6
D.5
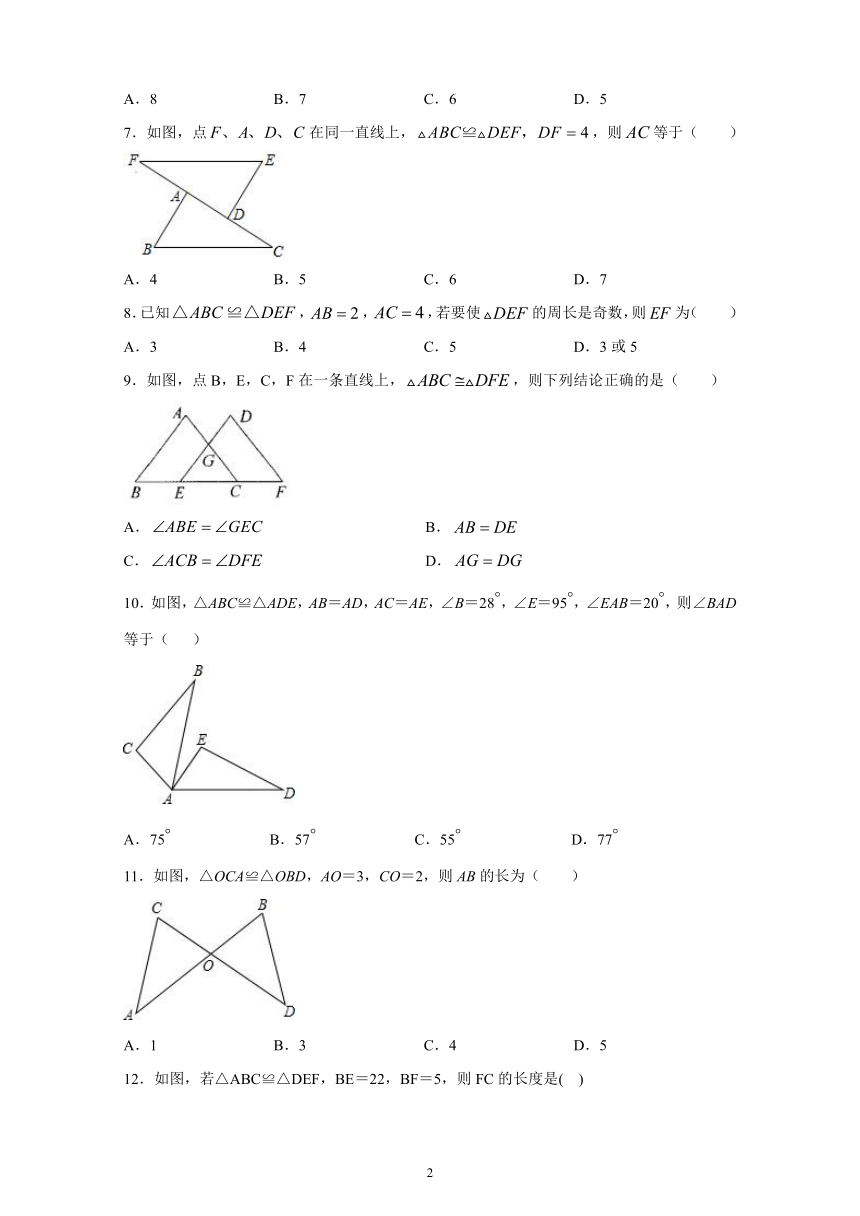
7.如图,点在同一直线上,,则等于(
)
A.4
B.5
C.6
D.7
8.已知,,,若要使的周长是奇数,则为(
)
A.3
B.4
C.5
D.3或5
9.如图,点B,E,C,F在一条直线上,,则下列结论正确的是(
)
B.
C.
D.
10.如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=28,∠E=95,∠EAB=20,则∠BAD等于(
)
A.75
B.57
C.55
D.77
11.如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )
A.1
B.3
C.4
D.5
12.如图,若△ABC≌△DEF,BE=22,BF=5,则FC的长度是(
)
A.10
B.12
C.8
D.16
二、填空题
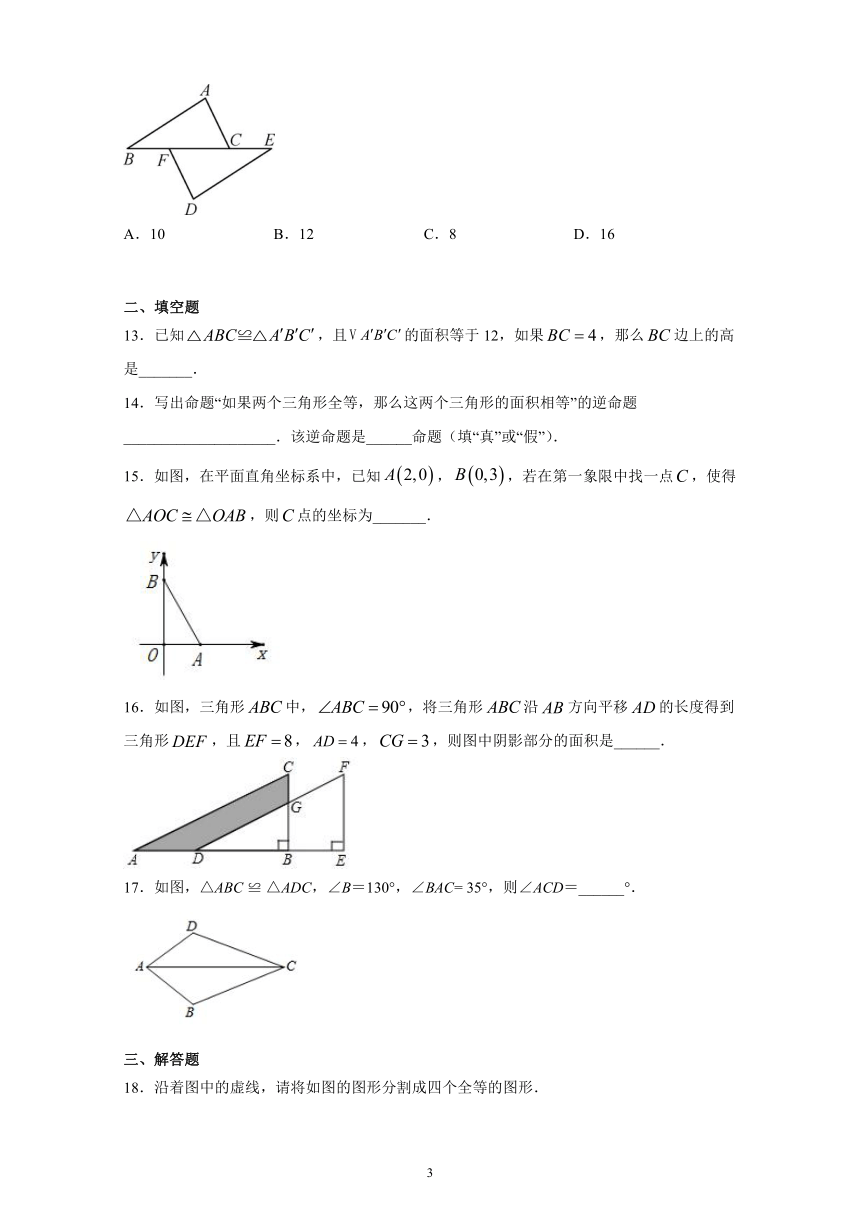
13.已知,且的面积等于12,如果,那么边上的高是_______.
14.写出命题“如果两个三角形全等,那么这两个三角形的面积相等”的逆命题____________________.该逆命题是______命题(填“真”或“假”).
15.如图,在平面直角坐标系中,已知,,若在第一象限中找一点,使得,则点的坐标为_______.
16.如图,三角形中,,将三角形沿方向平移的长度得到三角形,且,,,则图中阴影部分的面积是______.
17.如图,△ABC
≌
△ADC,∠B=130°,∠BAC=
35°,则∠ACD=______°.
三、解答题
18.沿着图中的虚线,请将如图的图形分割成四个全等的图形.
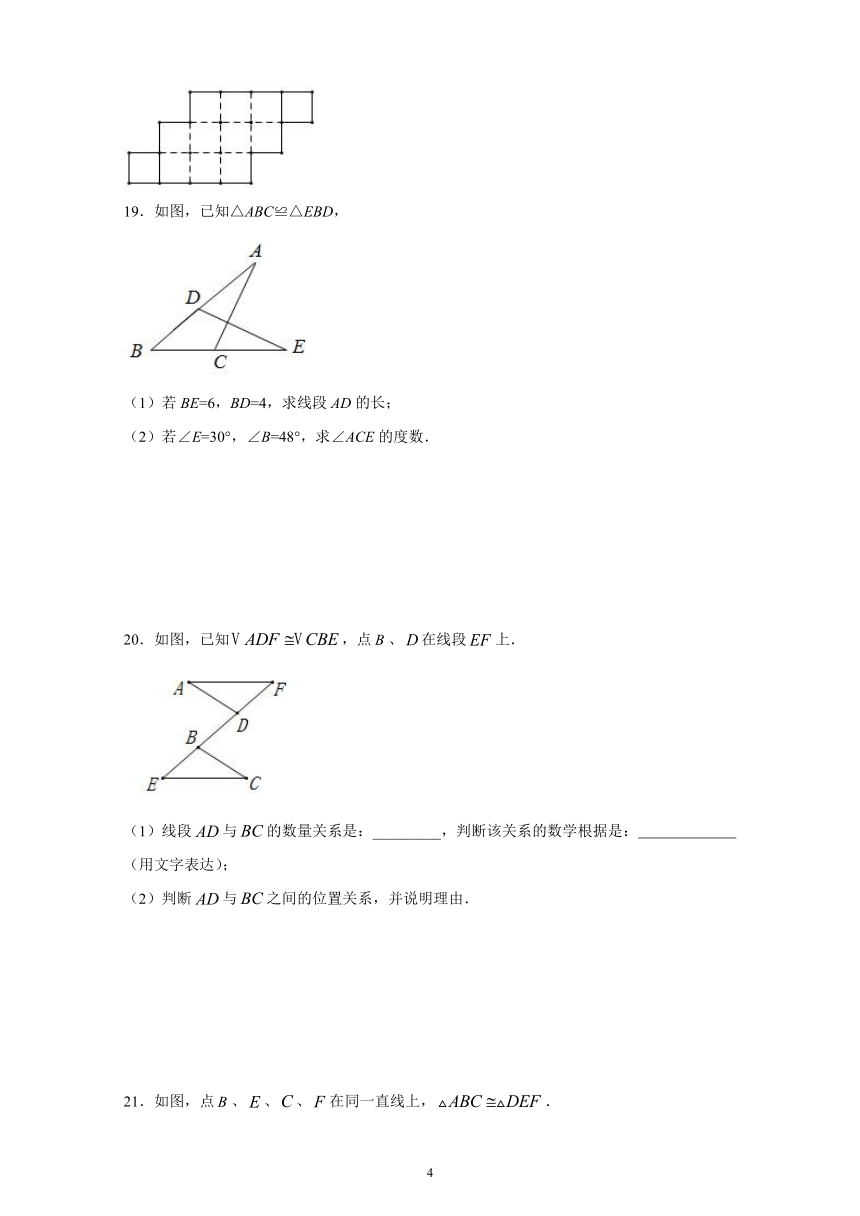
19.如图,已知△ABC≌△EBD,
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
20.如图,已知,点、在线段上.
(1)线段与的数量关系是:_________,判断该关系的数学根据是:
(用文字表达);
(2)判断与之间的位置关系,并说明理由.
21.如图,点、、、在同一直线上,.
(1)求证:.
(2)若与相交于点,,,求的长.
22.如图所示,,,三点在同一直线上,且.
(1)求证:;
(2)当满足什么条件时,?
参考答案
1.B
解:A、两个图形不能完全重合,故本选项错误;
B、两个图形能完全重合,故本选项正确;
C、两个图形不能完全重合,故本选项错误;
D、两个图形不能完全重合,故本选项错误,
故选B.
2.D
解:全等三角形是指能够完全重合的三角形.
故选:D
3.D
解:两个形状相同的图形大小不一定相等,故本项错误;
两个正方形形状相同,但大小不一定相等,故本项错误;
全等图形形状大小都相同,故本项正确;
面积相等的两个三角形不一定全等,故本项错误.
综上可得只有正确.
故选D.
4.D
解:∵△ABC≌△DBE,
∴∠A=∠D=65°,
∴∠C=180°-∠ABC
-∠A=35°,
故选:D.
5.C
解:由图可知:(a)、(b)、(d)的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,根据等量减去等量差相等的原理得这三个图形中阴影部分的面积相等.
故选:.
6.B
解:∵△ABE≌△ACD,
∴BE=CD,
∴BE+CD=BC+DE=14,
∴2CD=14,
∴CD=7,
故选:B.
7.A
解:∵△ABC≌△DEF,DF=4,
∴AC=DF=4,
故选:A.
8.D
解:设三角形ABC的第三边长为x,
则2<x<6,
∵的周长是奇数,
∴第三边为奇数,
∴x=3或x=5,
∴选D.
9.D
解:∵△ABC≌△DFE,
∴∠ABC=∠DFE,AB=DF,∠ACB=∠GEC,
故A、B、C选项均不正确,不符合题意;
∵∠ACB=∠GEC,
∴GE=GC,
∵△ABC≌△DFE,
∴AC=DE,
∴AC-GC=DE-GE,
∴AG=DG,故D选项符合题意.
故选:D.
10.D
解:∵△ABC≌△ADE,
∴∠B=∠D=28°,
又∵∠D+∠E+∠DAE=180°,∠E=95°,
∴∠DAE=180°-28°-95°=57°,
∵∠EAB=20°,
∴∠BAD=∠DAE+∠EAB=77°.
故选:D.
11.D
∵△OCA≌△OBD,
∴CO=BO=2,
∴AB=AO+BO=2+3=5,
故选:D.
12.B
解:∵BE=22,BF=5,
∴EF=BE-BF=17,
∵△ABC≌△DEF,
∴BC=EF=17,
∴FC=BC-BF=12.
故选:B
13.6
解:∵,的面积等于12,
∴的面积等于12,
∵BC=4,
∴BC边上的高是=6,
故答案为:6.
14.如果两个三角形的面积相等,那么这两个三角形全等
假
解:“如果两个三角形全等,那么这两个三角形的面积相等.”写成它的逆命题:如果两个三角形的面积相等,那么这两个三角形全等,该逆命题是假命题,
故答案为:如果两个三角形的面积相等,那么这两个三角形全等;假.
15.
解:根据题意C点在第一象限内,且,
如图,又已知和有已知公共边AO,
∴.
故答案为.
16.26
解:∵三角形ABC沿AB方向平移AD的长度得到三角形DEF,
∴△ABC≌△DEF,BC=EF=8,AD=BE=4
∴BG=BC-CG=8-3=5,
∵S阴影部分+S△DBG=S△DBG+S梯形BEFG,
∴S阴影部分=S梯形BEFG=(5+8)×4=26.
故答案为:26.
17.
解:
△ABC
≌
△ADC,∠B=130°,∠BAC=
35°,
故答案为:15
18.见解析
解:共有个小正方形,
被分成四个全等的图形后每个图形有,
如图所示:
,
19.(1)2;(2)78°.
解:(1)∵△ABC≌△EBD,
∴AB=BE=6,
∵AD=AB-BD,BD=4,
∴AD=6-4=2;
(2)∵△ABC≌△EBD,
∴∠A=∠E=30°,
∵∠ACE=∠A+∠B,∠B=48°,
∴∠ACE=30°+48°
=78°.
20.(1)相等(或写),全等三角形的对应边相等;(2),见详解
解:(1)∵
∴AD=BC
根据全等三角形的对应边相等
故答案为:相等(或写)
全等三角形的对应边相等
(2)猜想:.
理由:
∵,
∴,
∵∠ADB=180°-∠ADF
∠CBD=180°-∠CBE
∴,
∴
故答案为
21.(1)见解析;(2)2
(1)证明:∵,
∴,
∴.
(2)解:∵,
∴.
∵,
∴.
22.(1)证明见解析;(2)为直角时,
(1)证明:∵,
∴AE=BC,AC=DE,
又∵,
∴.
(2)若,则,
又∵,
∴,
∴,
又∵,
∴,
即当满足为直角时,.
一、单选题
1.下列图形中,属于全等图形的是( )
A.
B.
C.
D.
2.全等三角形是(
)
A.面积相等的三角形
B.角相等的三角形
C.周长相等的三角形
D.完全重合的三角形
3.下列说法:两个形状相同的图形称为全等图形;两个正方形是全等图形;全等图形的形状、大小都相同;面积相等的两个三角形是全等图形其中,正确的是(????)
A.
B.
C.
D.
4.如图,,,,则的度数为(
)
A.20°
B.25°
C.30°
D.35°
5.如图,下面4个正方形的边长都相等,其中阴影部分的面积相等的图形有(
)
A.0个
B.2个
C.3个
D.4个
6.如图,△ABE≌△ACD,BC=10,DE=4,则DC的长是( )
A.8
B.7
C.6
D.5
7.如图,点在同一直线上,,则等于(
)
A.4
B.5
C.6
D.7
8.已知,,,若要使的周长是奇数,则为(
)
A.3
B.4
C.5
D.3或5
9.如图,点B,E,C,F在一条直线上,,则下列结论正确的是(
)
B.
C.
D.
10.如图,△ABC≌△ADE,AB=AD,AC=AE,∠B=28,∠E=95,∠EAB=20,则∠BAD等于(
)
A.75
B.57
C.55
D.77
11.如图,△OCA≌△OBD,AO=3,CO=2,则AB的长为( )
A.1
B.3
C.4
D.5
12.如图,若△ABC≌△DEF,BE=22,BF=5,则FC的长度是(
)
A.10
B.12
C.8
D.16
二、填空题
13.已知,且的面积等于12,如果,那么边上的高是_______.
14.写出命题“如果两个三角形全等,那么这两个三角形的面积相等”的逆命题____________________.该逆命题是______命题(填“真”或“假”).
15.如图,在平面直角坐标系中,已知,,若在第一象限中找一点,使得,则点的坐标为_______.
16.如图,三角形中,,将三角形沿方向平移的长度得到三角形,且,,,则图中阴影部分的面积是______.
17.如图,△ABC
≌
△ADC,∠B=130°,∠BAC=
35°,则∠ACD=______°.
三、解答题
18.沿着图中的虚线,请将如图的图形分割成四个全等的图形.
19.如图,已知△ABC≌△EBD,
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
20.如图,已知,点、在线段上.
(1)线段与的数量关系是:_________,判断该关系的数学根据是:
(用文字表达);
(2)判断与之间的位置关系,并说明理由.
21.如图,点、、、在同一直线上,.
(1)求证:.
(2)若与相交于点,,,求的长.
22.如图所示,,,三点在同一直线上,且.
(1)求证:;
(2)当满足什么条件时,?
参考答案
1.B
解:A、两个图形不能完全重合,故本选项错误;
B、两个图形能完全重合,故本选项正确;
C、两个图形不能完全重合,故本选项错误;
D、两个图形不能完全重合,故本选项错误,
故选B.
2.D
解:全等三角形是指能够完全重合的三角形.
故选:D
3.D
解:两个形状相同的图形大小不一定相等,故本项错误;
两个正方形形状相同,但大小不一定相等,故本项错误;
全等图形形状大小都相同,故本项正确;
面积相等的两个三角形不一定全等,故本项错误.
综上可得只有正确.
故选D.
4.D
解:∵△ABC≌△DBE,
∴∠A=∠D=65°,
∴∠C=180°-∠ABC
-∠A=35°,
故选:D.
5.C
解:由图可知:(a)、(b)、(d)的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,根据等量减去等量差相等的原理得这三个图形中阴影部分的面积相等.
故选:.
6.B
解:∵△ABE≌△ACD,
∴BE=CD,
∴BE+CD=BC+DE=14,
∴2CD=14,
∴CD=7,
故选:B.
7.A
解:∵△ABC≌△DEF,DF=4,
∴AC=DF=4,
故选:A.
8.D
解:设三角形ABC的第三边长为x,
则2<x<6,
∵的周长是奇数,
∴第三边为奇数,
∴x=3或x=5,
∴选D.
9.D
解:∵△ABC≌△DFE,
∴∠ABC=∠DFE,AB=DF,∠ACB=∠GEC,
故A、B、C选项均不正确,不符合题意;
∵∠ACB=∠GEC,
∴GE=GC,
∵△ABC≌△DFE,
∴AC=DE,
∴AC-GC=DE-GE,
∴AG=DG,故D选项符合题意.
故选:D.
10.D
解:∵△ABC≌△ADE,
∴∠B=∠D=28°,
又∵∠D+∠E+∠DAE=180°,∠E=95°,
∴∠DAE=180°-28°-95°=57°,
∵∠EAB=20°,
∴∠BAD=∠DAE+∠EAB=77°.
故选:D.
11.D
∵△OCA≌△OBD,
∴CO=BO=2,
∴AB=AO+BO=2+3=5,
故选:D.
12.B
解:∵BE=22,BF=5,
∴EF=BE-BF=17,
∵△ABC≌△DEF,
∴BC=EF=17,
∴FC=BC-BF=12.
故选:B
13.6
解:∵,的面积等于12,
∴的面积等于12,
∵BC=4,
∴BC边上的高是=6,
故答案为:6.
14.如果两个三角形的面积相等,那么这两个三角形全等
假
解:“如果两个三角形全等,那么这两个三角形的面积相等.”写成它的逆命题:如果两个三角形的面积相等,那么这两个三角形全等,该逆命题是假命题,
故答案为:如果两个三角形的面积相等,那么这两个三角形全等;假.
15.
解:根据题意C点在第一象限内,且,
如图,又已知和有已知公共边AO,
∴.
故答案为.
16.26
解:∵三角形ABC沿AB方向平移AD的长度得到三角形DEF,
∴△ABC≌△DEF,BC=EF=8,AD=BE=4
∴BG=BC-CG=8-3=5,
∵S阴影部分+S△DBG=S△DBG+S梯形BEFG,
∴S阴影部分=S梯形BEFG=(5+8)×4=26.
故答案为:26.
17.
解:
△ABC
≌
△ADC,∠B=130°,∠BAC=
35°,
故答案为:15
18.见解析
解:共有个小正方形,
被分成四个全等的图形后每个图形有,
如图所示:
,
19.(1)2;(2)78°.
解:(1)∵△ABC≌△EBD,
∴AB=BE=6,
∵AD=AB-BD,BD=4,
∴AD=6-4=2;
(2)∵△ABC≌△EBD,
∴∠A=∠E=30°,
∵∠ACE=∠A+∠B,∠B=48°,
∴∠ACE=30°+48°
=78°.
20.(1)相等(或写),全等三角形的对应边相等;(2),见详解
解:(1)∵
∴AD=BC
根据全等三角形的对应边相等
故答案为:相等(或写)
全等三角形的对应边相等
(2)猜想:.
理由:
∵,
∴,
∵∠ADB=180°-∠ADF
∠CBD=180°-∠CBE
∴,
∴
故答案为
21.(1)见解析;(2)2
(1)证明:∵,
∴,
∴.
(2)解:∵,
∴.
∵,
∴.
22.(1)证明见解析;(2)为直角时,
(1)证明:∵,
∴AE=BC,AC=DE,
又∵,
∴.
(2)若,则,
又∵,
∴,
∴,
又∵,
∴,
即当满足为直角时,.
