2.3平面向量的基本定理及坐标表示(一) PPT课件
文档属性
| 名称 | 2.3平面向量的基本定理及坐标表示(一) PPT课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 801.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-18 09:47:08 | ||
图片预览



文档简介
(共62张PPT)
2.3平面向量的基本
定理及坐标表示
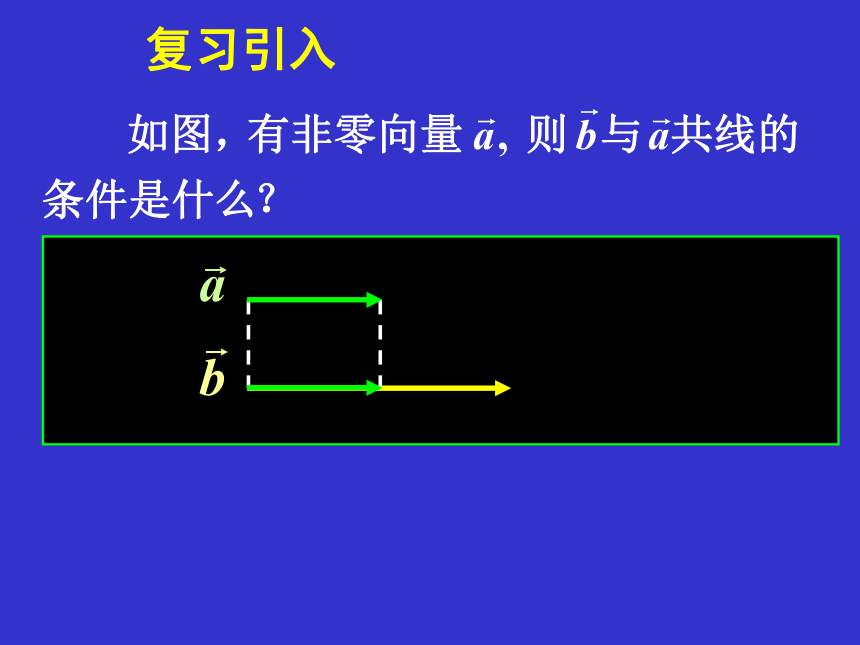
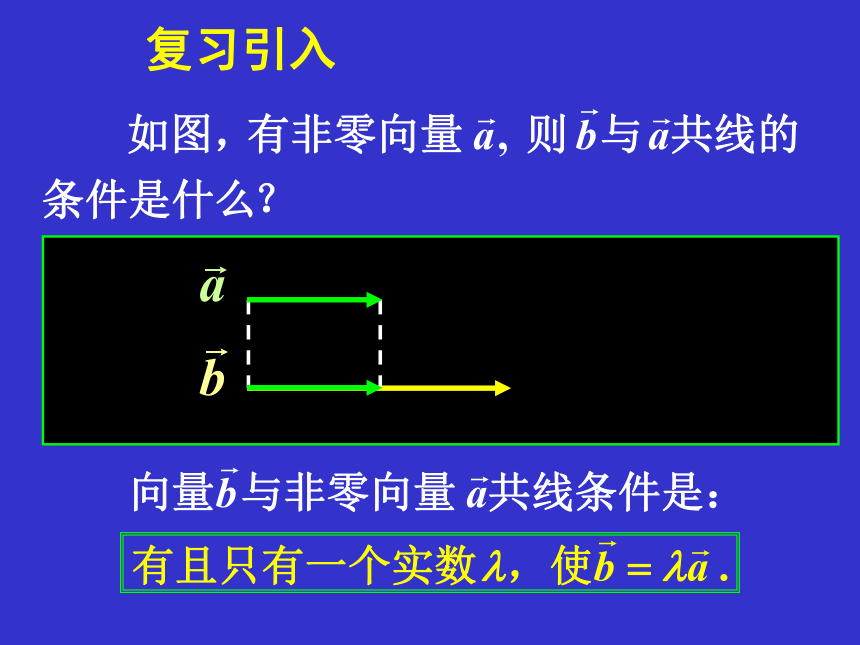
复习引入
复习引入
思考:
给定平面内两个向量
向量
(2) 同一平面内的任一向量是否都可以用
形如 的向量表示?
请你作出
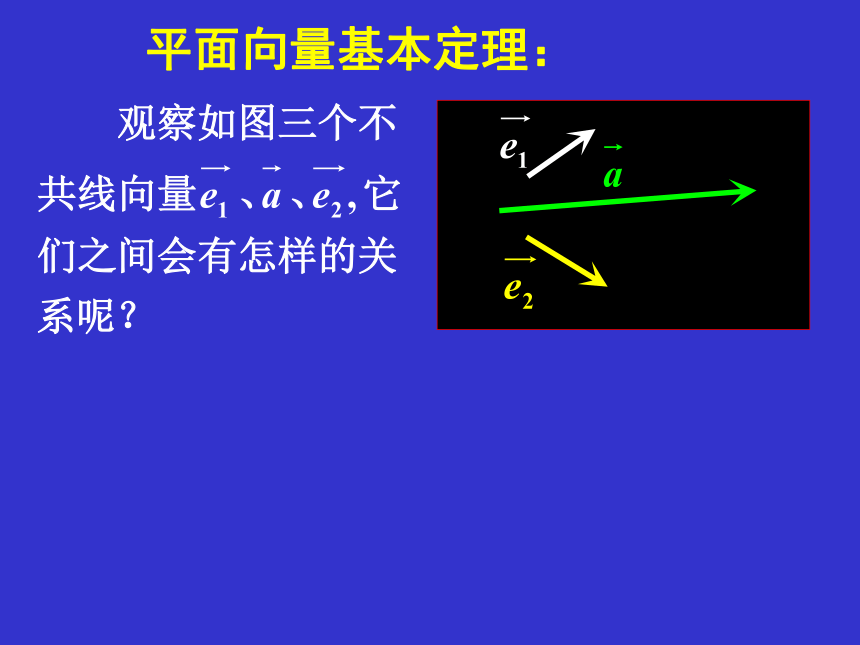
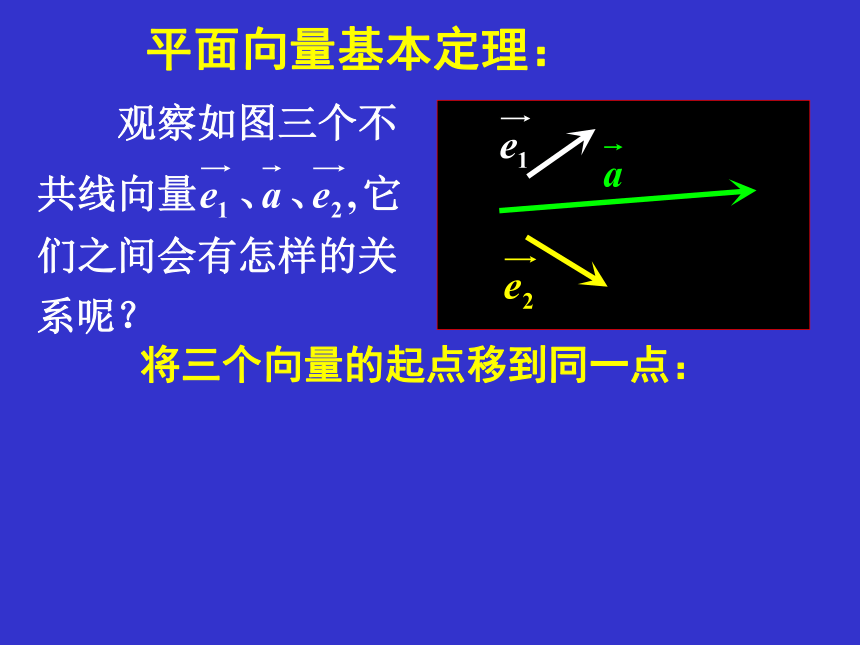
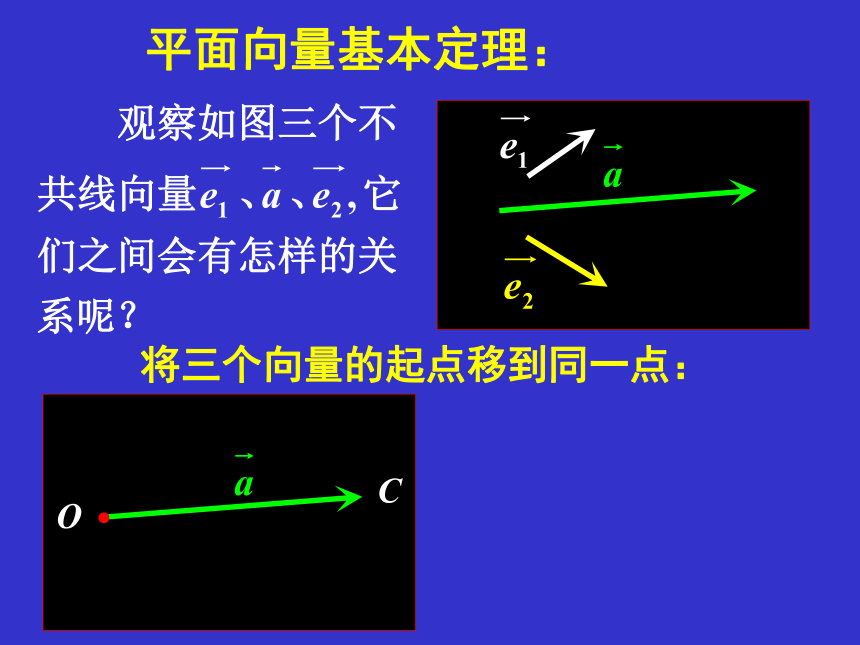
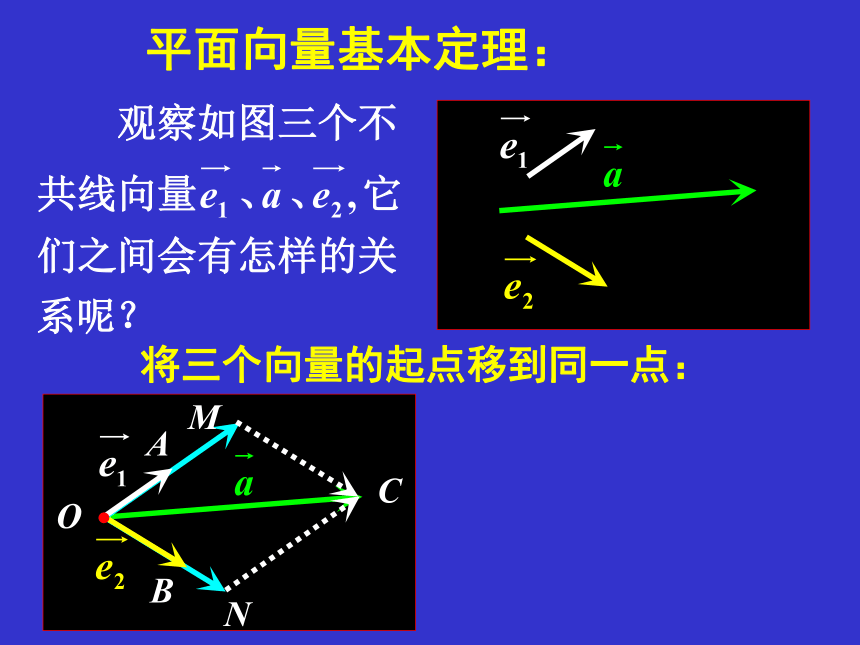
平面向量基本定理:
平面向量基本定理:
将三个向量的起点移到同一点:
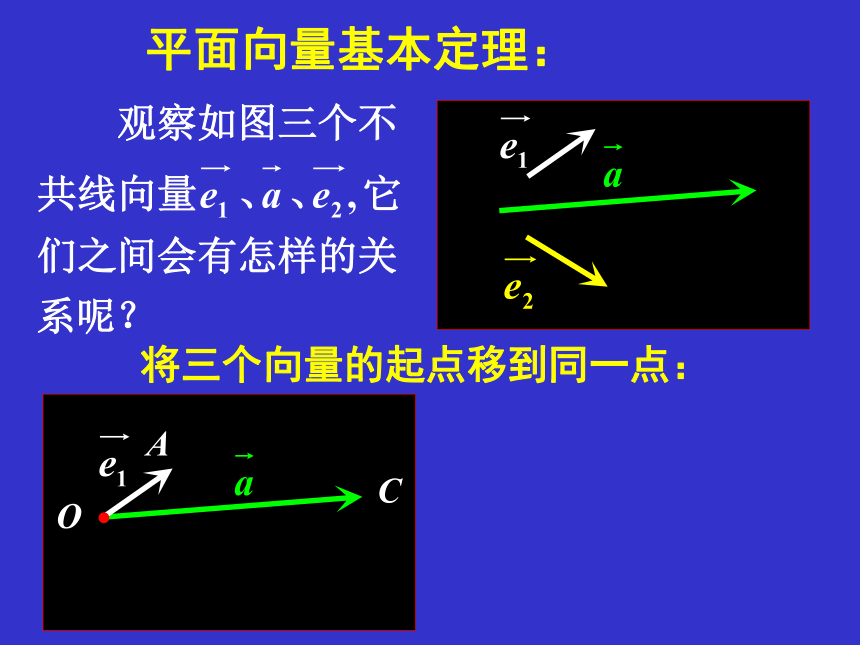
平面向量基本定理:
将三个向量的起点移到同一点:
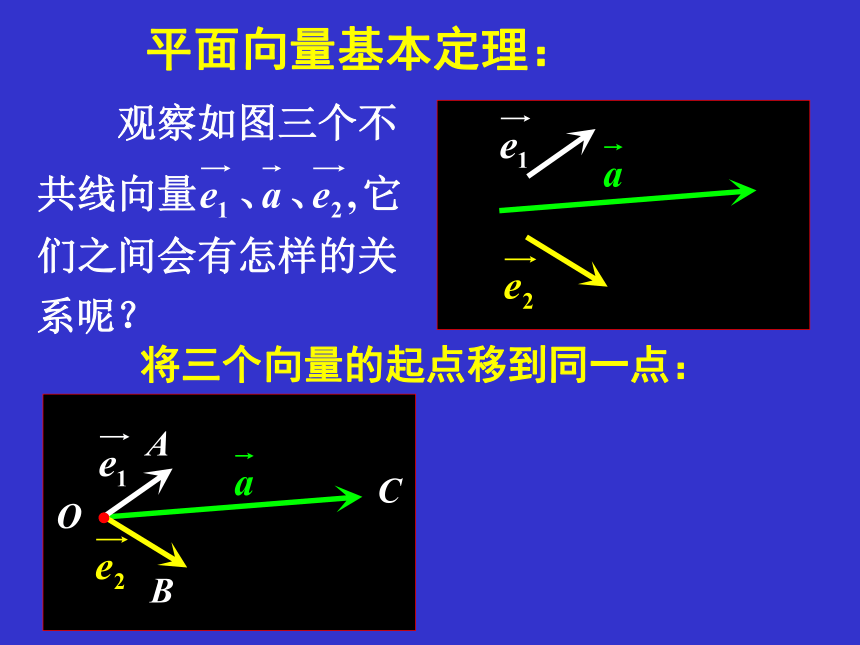
平面向量基本定理:
将三个向量的起点移到同一点:
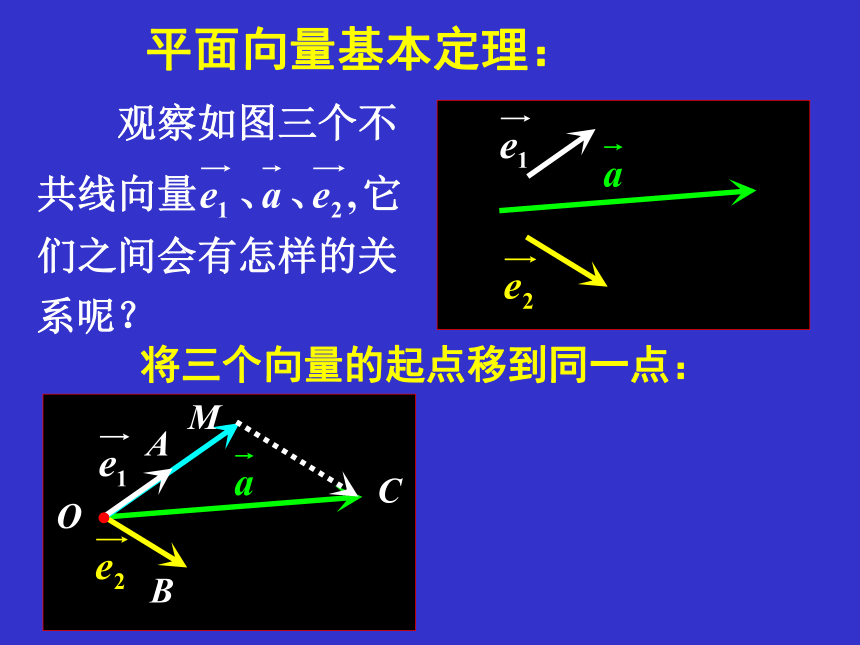
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
归纳:
想一想:
讨论:
⑴
⑵
讨论:
O
⑵
讨论:
O
⑵
讨论:
O
⑵
讨论:
O
⑵
O
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
平面向量基本定理:
平面向量基本定理:
问题一:
问题一:
基底不共线也不唯一,任意
两个不共线的向量均可作基底.
问题二:
给定基底后,任意一个向量的
表示是唯一的.
问题二:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
A
B
D
C
M
定理的应用:
O
A
B
P
定理的应用:
O
A
B
P
定理的应用:
O
A
B
P
向量的夹角:
向量的坐标表示
向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
应用:
平面向量基本定理;
2. 平面向量的坐标的概念;
课堂小结
阅读教材P.93到P.96;
2. 《习案》作业二十.
课后作业
2.3平面向量的基本
定理及坐标表示
复习引入
复习引入
思考:
给定平面内两个向量
向量
(2) 同一平面内的任一向量是否都可以用
形如 的向量表示?
请你作出
平面向量基本定理:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
平面向量基本定理:
将三个向量的起点移到同一点:
归纳:
想一想:
讨论:
⑴
⑵
讨论:
O
⑵
讨论:
O
⑵
讨论:
O
⑵
讨论:
O
⑵
O
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
⑶
讨论:
平面向量基本定理:
平面向量基本定理:
问题一:
问题一:
基底不共线也不唯一,任意
两个不共线的向量均可作基底.
问题二:
给定基底后,任意一个向量的
表示是唯一的.
问题二:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
定理的应用:
A
B
D
C
M
定理的应用:
O
A
B
P
定理的应用:
O
A
B
P
定理的应用:
O
A
B
P
向量的夹角:
向量的坐标表示
向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
平面向量的坐标表示
应用:
平面向量基本定理;
2. 平面向量的坐标的概念;
课堂小结
阅读教材P.93到P.96;
2. 《习案》作业二十.
课后作业
