1.4.1正弦函数、余弦函数的图象
文档属性
| 名称 | 1.4.1正弦函数、余弦函数的图象 |  | |
| 格式 | zip | ||
| 文件大小 | 219.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-18 09:47:08 | ||
图片预览





文档简介
(共49张PPT)
复习引入
1. 弧度定义;
2. 正、余弦函数定义;
3. 正、余弦线.
讲授新课
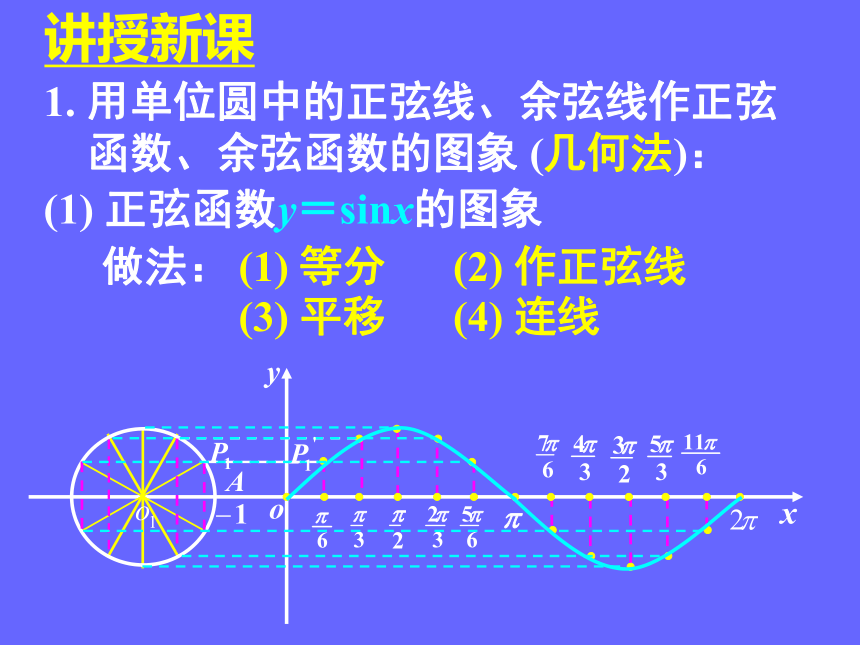
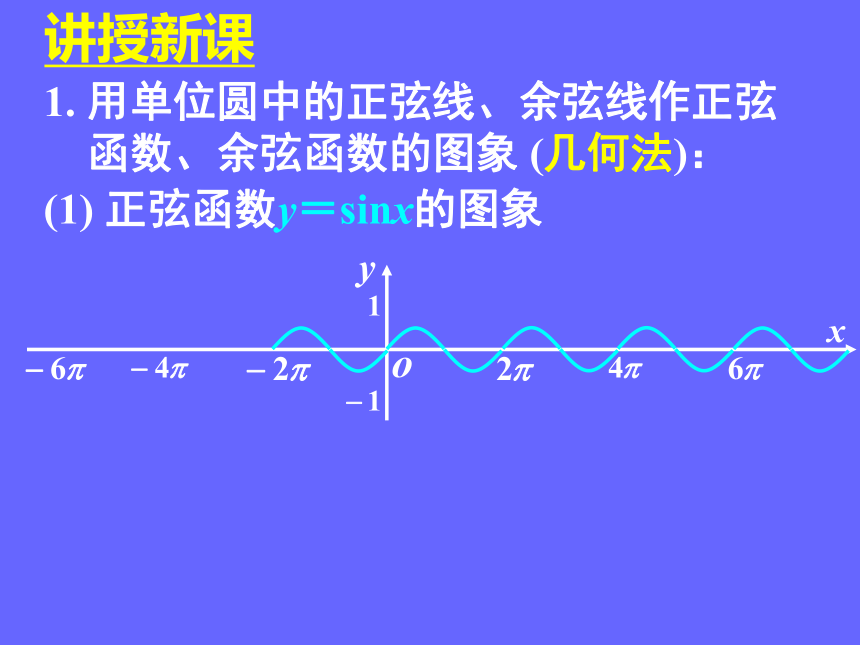
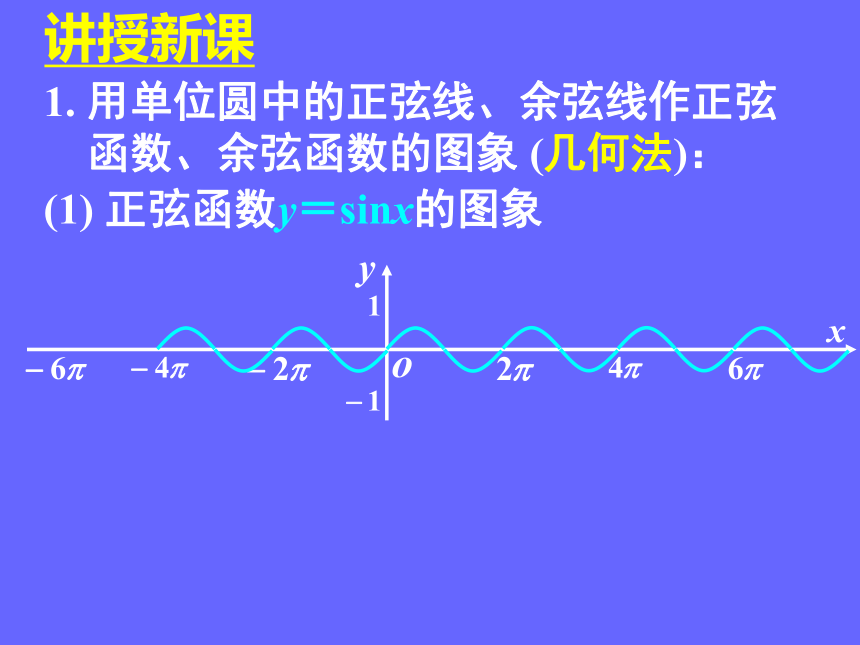
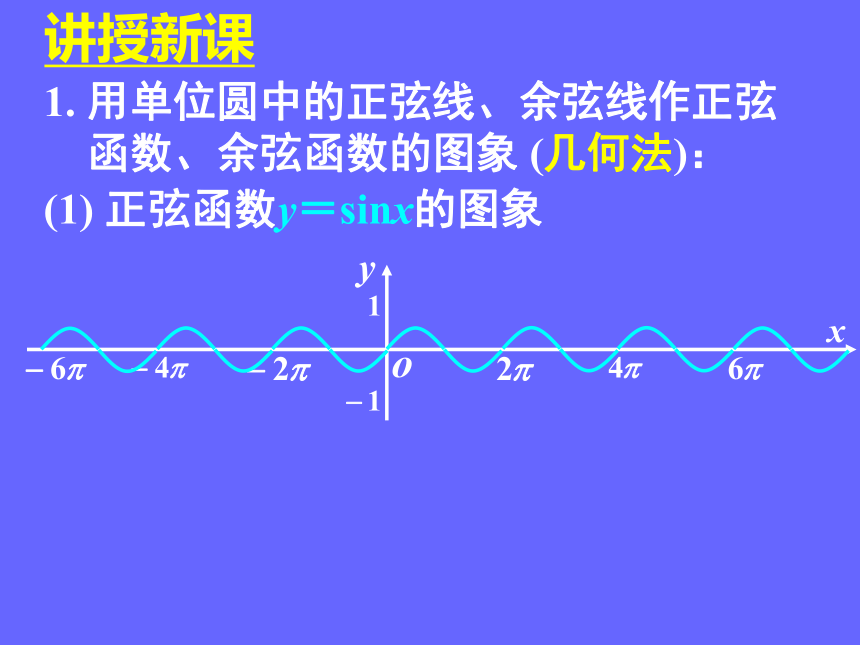
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 等分
(2) 作正弦线
(3) 平移
(4) 连线
做法:
(1) 正弦函数y=sinx的图象
讲授新课
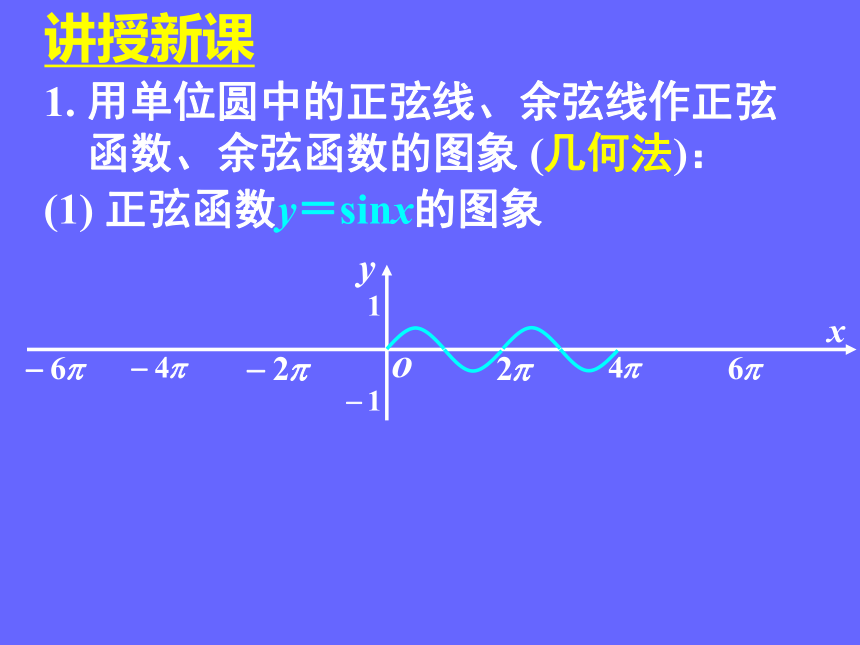
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
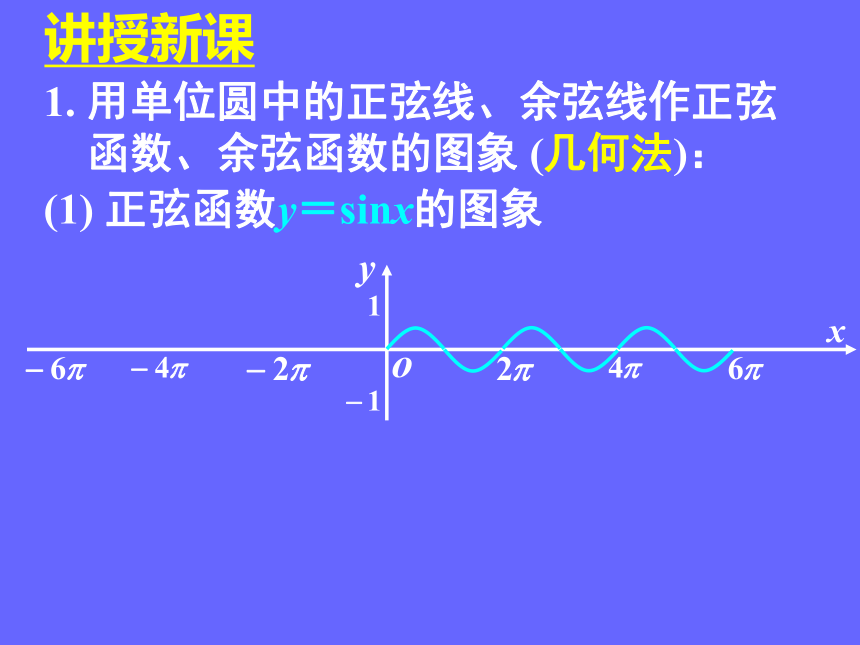
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
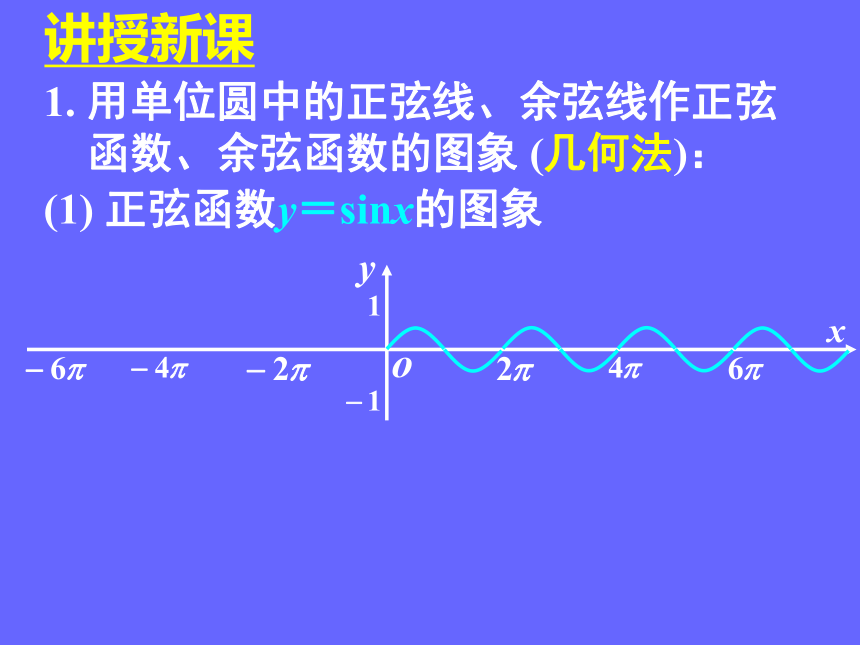
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(2) 余弦函数y=cosx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(2) 余弦函数y=cosx的图象
你能根据诱导公式,以正弦函数图象
为基础,通过适当的图形变换得到余弦函
数的图象?
探究 1:
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(2) 余弦函数y=cosx的图象
讲授新课
(2) y=cosx
(1) y=sinx
讲授新课
(2) y=cosx
(1) y=sinx
正弦函数y=sinx的图象和余弦函数
y=cosx的图象分别叫做正弦曲线和余弦
曲线.
讲授新课
在作正弦函数的图象时,应抓住哪些
关键点
思考:
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
余弦函数y=cosx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
余弦函数y=cosx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
讲授新课
例1. 作下列函数的简图
(1) y=1+sinx,x∈[0,2 ];
(2) y=-cosx,x∈[0,2 ].
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
函数值加减,图象上下移动;
自变量加减,图象左右移动.
小结:
探究3.
讲授新课
如何利用y=cosx, x∈[0, 2 ]的图
象,通过图形变换(平移、翻转等)来得
到y=-cosx,x∈[0, 2 ]的图象?
如何利用y=cosx, x∈[0, 2 ]的图
象,通过图形变换(平移、翻转等)来得
到y=-cosx,x∈[0, 2 ]的图象?
探究3.
这两个图象关于x轴对称.
小结:
讲授新课
探究4.
讲授新课
如何利用y=cos x,x∈[0, 2 ]的图
象,通过图形变换(平移、翻转等)来得
到y=2-cosx,x∈[0, 2 ]的图象?
如何利用y=cos x,x∈[0, 2 ]的图
象,通过图形变换(平移、翻转等)来得
到y=2-cosx,x∈[0, 2 ]的图象?
探究4.
讲授新课
先作y=cosx图象关于x轴对称的图形,
得到y=-cosx的图象,再将y=-cosx的
图象向上平移2个单位,得到 y=2-cosx
的图象.
小结:
探究5.
讲授新课
不用作图, 你能判断函数
和y=cosx的图象有何关系吗 请在同一坐
标系中画出它们的简图, 以验证你的猜想.
探究5.
讲授新课
不用作图, 你能判断函数
和y=cosx的图象有何关系吗 请在同一坐
标系中画出它们的简图, 以验证你的猜想.
小结:
探究5.
讲授新课
不用作图, 你能判断函数
和y=cosx的图象有何关系吗 请在同一坐
标系中画出它们的简图, 以验证你的猜想.
小结:
这两个函数相等,图象重合.
思考题. 分别利用函数的图象和三角函数
线两种方法,求满足下列条件的x的集合:
讲授新课
课堂小结
1. 正弦、余弦曲线几何画法和五点法;
2. 注意与诱导公式,三角函数线的知识
的联系.
课后作业
阅读教材P.30-P.33;
《习案》作业八.
复习引入
1. 弧度定义;
2. 正、余弦函数定义;
3. 正、余弦线.
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 等分
(2) 作正弦线
(3) 平移
(4) 连线
做法:
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(1) 正弦函数y=sinx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(2) 余弦函数y=cosx的图象
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(2) 余弦函数y=cosx的图象
你能根据诱导公式,以正弦函数图象
为基础,通过适当的图形变换得到余弦函
数的图象?
探究 1:
讲授新课
1. 用单位圆中的正弦线、余弦线作正弦
函数、余弦函数的图象 (几何法):
(2) 余弦函数y=cosx的图象
讲授新课
(2) y=cosx
(1) y=sinx
讲授新课
(2) y=cosx
(1) y=sinx
正弦函数y=sinx的图象和余弦函数
y=cosx的图象分别叫做正弦曲线和余弦
曲线.
讲授新课
在作正弦函数的图象时,应抓住哪些
关键点
思考:
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
余弦函数y=cosx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
讲授新课
2. 用五点法作正弦函数和余弦函数的简
图 (描点法):
正弦函数y=sinx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
余弦函数y=cosx,x∈[0, 2 ]的图象中,
五个关键点是哪几个
讲授新课
例1. 作下列函数的简图
(1) y=1+sinx,x∈[0,2 ];
(2) y=-cosx,x∈[0,2 ].
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
讲授新课
函数值加减,图象上下移动;
自变量加减,图象左右移动.
小结:
探究3.
讲授新课
如何利用y=cosx, x∈[0, 2 ]的图
象,通过图形变换(平移、翻转等)来得
到y=-cosx,x∈[0, 2 ]的图象?
如何利用y=cosx, x∈[0, 2 ]的图
象,通过图形变换(平移、翻转等)来得
到y=-cosx,x∈[0, 2 ]的图象?
探究3.
这两个图象关于x轴对称.
小结:
讲授新课
探究4.
讲授新课
如何利用y=cos x,x∈[0, 2 ]的图
象,通过图形变换(平移、翻转等)来得
到y=2-cosx,x∈[0, 2 ]的图象?
如何利用y=cos x,x∈[0, 2 ]的图
象,通过图形变换(平移、翻转等)来得
到y=2-cosx,x∈[0, 2 ]的图象?
探究4.
讲授新课
先作y=cosx图象关于x轴对称的图形,
得到y=-cosx的图象,再将y=-cosx的
图象向上平移2个单位,得到 y=2-cosx
的图象.
小结:
探究5.
讲授新课
不用作图, 你能判断函数
和y=cosx的图象有何关系吗 请在同一坐
标系中画出它们的简图, 以验证你的猜想.
探究5.
讲授新课
不用作图, 你能判断函数
和y=cosx的图象有何关系吗 请在同一坐
标系中画出它们的简图, 以验证你的猜想.
小结:
探究5.
讲授新课
不用作图, 你能判断函数
和y=cosx的图象有何关系吗 请在同一坐
标系中画出它们的简图, 以验证你的猜想.
小结:
这两个函数相等,图象重合.
思考题. 分别利用函数的图象和三角函数
线两种方法,求满足下列条件的x的集合:
讲授新课
课堂小结
1. 正弦、余弦曲线几何画法和五点法;
2. 注意与诱导公式,三角函数线的知识
的联系.
课后作业
阅读教材P.30-P.33;
《习案》作业八.
