苏科版九年级上册数学第2章 对称图形——圆 2.7弧长及扇形的面积 学案
文档属性
| 名称 | 苏科版九年级上册数学第2章 对称图形——圆 2.7弧长及扇形的面积 学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 196.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 06:49:09 | ||
图片预览

文档简介
弧长和扇形的面积
一、学习目标:
1.经历探索弧长计算公式及扇形面积计算公式的过程。
2.了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题。
二、学习重点:弧长与扇形的计算公式。
三、学习难点:弧长与扇形的计算公式的推导与应用。
四、教学过程:
(一)创设情境
1.小学里我们已经学习过圆周长公式、圆面积公式。
你能说出圆周长与圆面积公式吗?
圆周长与半径之间关系为:
圆面积与半径之间关系为:
2.上节课我们将一个圆()等分,依次连接各等分点所得的多边形是这个圆的内接正多边形。类比数学方法,尝试解决问题:
(二)归纳尝试
1.弧长计算公式
(1)360°的圆心角所对弧长就是圆周长;
(2)1°的圆心角所对的弧长是,即;
(3)°的圆心角所对的弧长为:。
注:应用“方程的观点”认识弧长计算公式,它揭示了、、这3个量之间的恒等关系。如果、、中,任意知道两个量,就可以根据公式求出另一个量。
例1、圆弧半径为24,所对圆心角为60°,则该圆心角所对弧长为: 。
例2、若扇形的圆心角为120°,弧长为,则扇形所在圆的半径为: 。
2.扇形面积计算公式
(1)360°的圆心角所在的扇形面积就是圆面积;
(2)1°的圆心角所在的扇形面积是;
(3)°的圆心角所在的扇形面积为:。
注:扇形面积公式是表示、、三个量之间的相等关系,在、、中任意知道两个就可以求出第三个值。
例3、若扇形的圆心角为72°,所在圆半径长为5,则扇形面积为: 。
例4、若扇形的圆心角为120°,弧长为,则扇形面积为: 。
(三)探求新知:
1、比较扇形面积计算公式与弧长计算公式,你发现有怎样的特征,结合图形用数学符号表述你的发现。
符号表述:
语言描述:
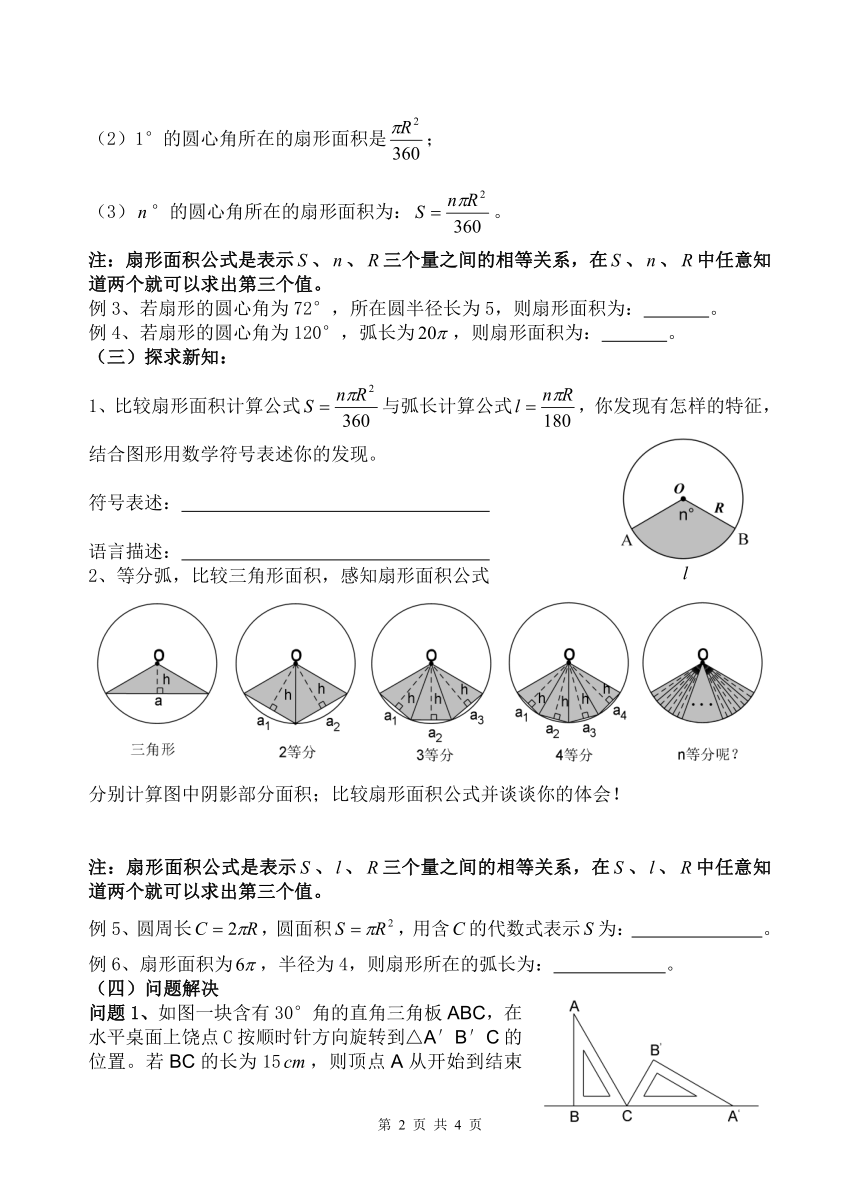
2、等分弧,比较三角形面积,感知扇形面积公式
分别计算图中阴影部分面积;比较扇形面积公式并谈谈你的体会!
注:扇形面积公式是表示、、三个量之间的相等关系,在、、中任意知道两个就可以求出第三个值。
例5、圆周长,圆面积,用含的代数式表示为: 。
例6、扇形面积为,半径为4,则扇形所在的弧长为: 。
(四)问题解决
问题1、如图一块含有30°角的直角三角板ABC,在水平桌面上饶点C按顺时针方向旋转到△A′B′C的位置。若BC的长为15,则顶点A从开始到结束所经过的路径长为 ( )
A. B. C. D.
问题2、如图,有一长为,宽为的长方形木板在桌面上做无滑动的顺时针方向翻滚,木板上的顶点A的位置变化为A→A1→A2,其中第二次翻滚被桌面上一小块木块挡住,使木块边沿A2C与桌面成30°角,则点A翻滚到点A2位置时,共走过的路径长为( )
A. B. C. D.
问题3、如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,切点为C。设弦AB的长为,圆环面积与之间有怎样的数量关系?
问题4、如图,正三角形ABC的边长为,分别以A、B、C为圆心,为半径的圆两两相切于点D、E、F。求、、围成的图形面积(图中阴影部分)。
思考题:如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC//AD,CD//AB。
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若的半径为1,求图中阴影部分的面积(结果保留)。
(五)课堂小结
1、弧长计算公式的推导和应用;
2、扇形面积计算公式和的推导和应用。
第 4 页 共 4 页
一、学习目标:
1.经历探索弧长计算公式及扇形面积计算公式的过程。
2.了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题。
二、学习重点:弧长与扇形的计算公式。
三、学习难点:弧长与扇形的计算公式的推导与应用。
四、教学过程:
(一)创设情境
1.小学里我们已经学习过圆周长公式、圆面积公式。
你能说出圆周长与圆面积公式吗?
圆周长与半径之间关系为:
圆面积与半径之间关系为:
2.上节课我们将一个圆()等分,依次连接各等分点所得的多边形是这个圆的内接正多边形。类比数学方法,尝试解决问题:
(二)归纳尝试
1.弧长计算公式
(1)360°的圆心角所对弧长就是圆周长;
(2)1°的圆心角所对的弧长是,即;
(3)°的圆心角所对的弧长为:。
注:应用“方程的观点”认识弧长计算公式,它揭示了、、这3个量之间的恒等关系。如果、、中,任意知道两个量,就可以根据公式求出另一个量。
例1、圆弧半径为24,所对圆心角为60°,则该圆心角所对弧长为: 。
例2、若扇形的圆心角为120°,弧长为,则扇形所在圆的半径为: 。
2.扇形面积计算公式
(1)360°的圆心角所在的扇形面积就是圆面积;
(2)1°的圆心角所在的扇形面积是;
(3)°的圆心角所在的扇形面积为:。
注:扇形面积公式是表示、、三个量之间的相等关系,在、、中任意知道两个就可以求出第三个值。
例3、若扇形的圆心角为72°,所在圆半径长为5,则扇形面积为: 。
例4、若扇形的圆心角为120°,弧长为,则扇形面积为: 。
(三)探求新知:
1、比较扇形面积计算公式与弧长计算公式,你发现有怎样的特征,结合图形用数学符号表述你的发现。
符号表述:
语言描述:
2、等分弧,比较三角形面积,感知扇形面积公式
分别计算图中阴影部分面积;比较扇形面积公式并谈谈你的体会!
注:扇形面积公式是表示、、三个量之间的相等关系,在、、中任意知道两个就可以求出第三个值。
例5、圆周长,圆面积,用含的代数式表示为: 。
例6、扇形面积为,半径为4,则扇形所在的弧长为: 。
(四)问题解决
问题1、如图一块含有30°角的直角三角板ABC,在水平桌面上饶点C按顺时针方向旋转到△A′B′C的位置。若BC的长为15,则顶点A从开始到结束所经过的路径长为 ( )
A. B. C. D.
问题2、如图,有一长为,宽为的长方形木板在桌面上做无滑动的顺时针方向翻滚,木板上的顶点A的位置变化为A→A1→A2,其中第二次翻滚被桌面上一小块木块挡住,使木块边沿A2C与桌面成30°角,则点A翻滚到点A2位置时,共走过的路径长为( )
A. B. C. D.
问题3、如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,切点为C。设弦AB的长为,圆环面积与之间有怎样的数量关系?
问题4、如图,正三角形ABC的边长为,分别以A、B、C为圆心,为半径的圆两两相切于点D、E、F。求、、围成的图形面积(图中阴影部分)。
思考题:如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC//AD,CD//AB。
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若的半径为1,求图中阴影部分的面积(结果保留)。
(五)课堂小结
1、弧长计算公式的推导和应用;
2、扇形面积计算公式和的推导和应用。
第 4 页 共 4 页
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
