2021-2022学年沪科版数学七年级上册2.2整式的加减 单元测试自我综合评价(word版有答案)
文档属性
| 名称 | 2021-2022学年沪科版数学七年级上册2.2整式的加减 单元测试自我综合评价(word版有答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 84.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-23 00:00:00 | ||
图片预览



文档简介
第2章 整式加减 自我综合评价
一、选择题(每小题3分,共27分)
1.“比m的大3的数”用代数式表示是
( )
A.m-3
B.m
C.2m+3
D.m+3
2.在下列各组单项式中,不是同类项的是
( )
A.-x2y和-yx2
B.-3和100
C.-x2yz和和-xy2z
D.-abc和abc
3.关于多项式3x2+x-2,下列说法错误的是( )
A.这是一个二次三项式
B.二次项系数是3
C.一次项系数是1
D.常数项是2
4.下列各式中正确的是
( )
A.-(2x+5)=-2x+5
B.-(4x-2)=-2x+2
C.-a+b=-(a-b)
D.2-3x=-(3x+2)
5.下列运算中结果正确的是
( )
A.3a+2b=5ab
B.5y-3y=2
C.-3x+5x=-8x
D.3x2y-2x2y=x2y
6.当x=5时,(x2-x)-(x2-2x+1)等于
( )
A.-14
B.4
C.-4
D.1
7.小李编写了一段计算机程序,输入任意一个有理数,显示屏的结果总等于所输入有理数的平方与-2之和,当输入-3时,将所显示的结果再次输入,这时显示的结果应该是
( )
A.7
B.9
C.47
D.49
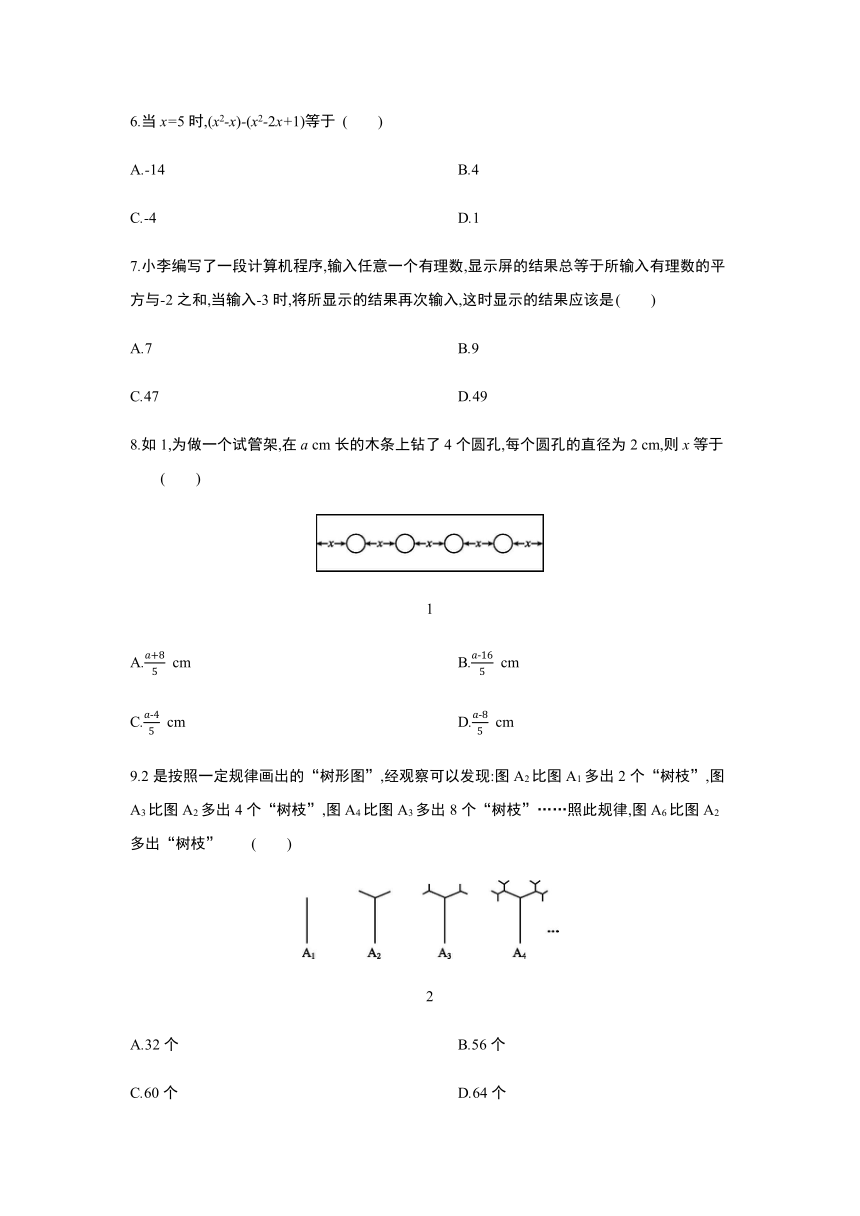
8.如1,为做一个试管架,在a
cm长的木条上钻了4个圆孔,每个圆孔的直径为2
cm,则x等于
( )
1
A.
cm
B.
cm
C.
cm
D.
cm
9.2是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”……照此规律,图A6比图A2多出“树枝”
( )
2
A.32个
B.56个
C.60个
D.64个
二、填空题(每小题4分,共24分)
10.单项式-的系数是 ,次数是 .?
11.如果-7+4ym+1-3y是三次三项式,那么m= .?
12.将多项式3x2-1-6x5-4x3按字母x的降幂排列为 .?
13.若单项式3xym与-xny2的和仍是单项式,则m+n的值是 .?
14.一个两位数,十位上的数字为x,个位上的数字比十位上的数字大3,则这个两位数可表示为 .?
15.观察下列等式:
12=1=×1×2×(2+1);
12+22=×2×3×(4+1);
12+22+32=×3×4×(6+1);
12+22+32+42=×4×5×(8+1);
…
可以推测12+22+32+…+n2=
.?
三、解答题(共49分)
16.(6分)计算:5(x+y)-3(2x-3y)-2(3x+2y).
17.(7分)先化简,再求值:已知x2-(2x2-4y)+2(x2-y),其中x=-1,y=.
18.(7分)小明在解数学题时,由于粗心,把原题“两个多项式A和B,其中B=4x2-5x-6,试求A+B”中的“A+B”错误地看成“A-B”,结果求出的答案是-7x2+10x+12,请你帮他算出A+B的正确答案.
19.(8分)已知A=x2+ax,B=2bx2-4x-1,且多项式2A+B的值与字母x的取值无关,求a,b的值.
20.(10分)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,如3:
3
(1)求所捂住的多项式;
(2)若x为正整数,任取x的几个值并求出所捂住多项式的值,你能发现什么规律?
(3)若所捂住多项式的值为144,请直接写出正整数x的值.
21.(11分)如4①,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”形图案,如图②所示,再将剪下的两个小长方形无缝隙、无重叠地拼接成一个新的长方形(如图③所示).
(1)这个新长方形的长和宽分别为 , ;(用含a,b的代数式表示)?
(2)若a=8x2+4x+1,b=-x2+3x-,求这个新长方形的周长;
(3)在(2)的条件下,当x=时,求这个新长方形的周长.
4
教师详解详析
【作者说卷】
本套试卷分三种题型:选择题、填空题和解答题,共21道题,其中易、中、难题之比为7∶2∶1.全面考查整式的加减各知识点,重点考查代数式的化简和求值.
1.D
2.C [解析]
所含字母相同,并且相同字母的指数也相同的项是同类项,且所有常数项都是同类项,只有C项中相同字母的指数不同,故不是同类项.
3.D [解析]
常数项是-2,不是2.
4.C
5.D
6.B
7.C
8.D
9.C [解析]
图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”……图A6比图A2多出“树枝”4+8+16+32=60(个).故选C.
10.- 3
11.2 [解析]
由题意知m+1=3,所以m=2.
12.-6x5-4x3+3x2-1
13.3 [解析]
由题意,得m=2,n=1,所以m+n=2+1=3.
14.11x+3 [解析]
十位上的数字是x,代表有x个10,个数上的数字是x+3,代表有x+3个1,故这个两位数是10x+(x+3)=11x+3.
15.n(n+1)(2n+1)
16.[解析]
先按照去括号法则去掉整式中的小括号,再合并整式中的同类项即可.
解:5(x+y)-3(2x-3y)-2(3x+2y)
=5x+5y-6x+9y-6x-4y
=-7x+10y.
17.解:原式=x2-2x2+4y+2x2-2y=x2+2y.
当x=-1,y=时,原式=1+1=2.
18.解:A+B=A-B+2B=(-7x2+10x+12)+2(4x2-5x-6)=x2.
19.解:因为A=x2+ax,B=2bx2-4x-1,
所以2A+B=2(x2+ax)+(2bx2-4x-1)
=2x2+2ax+2bx2-4x-1
=(2+2b)x2+(2a-4)x-1.
由结果与字母x的取值无关,
得2+2b=0,2a-4=0,解得a=2,b=-1.
20.解:(1)(-2x2+3x-6)-(-3x2+5x-7)
=-2x2+3x-6+3x2-5x+7
=x2-2x+1,
即所捂住的多项式是x2-2x+1.
(2)当x=1时,x2-2x+1=1-2+1=0;
当x=2时,x2-2x+1=4-4+1=1;
当x=3时,x2-2x+1=9-6+1=4;
当x=4时,x2-2x+1=16-8+1=9.
规律:所捂住多项式的值是代入的正整数x与1的差的平方.
(3)若所捂住多项式的值为144,则正整数x的值是13.
21.解:(1)由图可得,这个新长方形的长为(a-b)+(a-2b)=2a-3b,宽为(a-3b)×=a-b.
故答案为2a-3b,a-b.
(2)新长方形的周长是2a-3b+a-b×2=-×2=5a-9b.
当a=8x2+4x+1,b=-x2+3x-时,5a-9b=5(8x2+4x+1)-9-x2+3x-=40x2+20x+5+9x2-27x+=49x2-7x+.
(3)当x=时,49x2-7x+=49×2-7×+=-+=.
一、选择题(每小题3分,共27分)
1.“比m的大3的数”用代数式表示是
( )
A.m-3
B.m
C.2m+3
D.m+3
2.在下列各组单项式中,不是同类项的是
( )
A.-x2y和-yx2
B.-3和100
C.-x2yz和和-xy2z
D.-abc和abc
3.关于多项式3x2+x-2,下列说法错误的是( )
A.这是一个二次三项式
B.二次项系数是3
C.一次项系数是1
D.常数项是2
4.下列各式中正确的是
( )
A.-(2x+5)=-2x+5
B.-(4x-2)=-2x+2
C.-a+b=-(a-b)
D.2-3x=-(3x+2)
5.下列运算中结果正确的是
( )
A.3a+2b=5ab
B.5y-3y=2
C.-3x+5x=-8x
D.3x2y-2x2y=x2y
6.当x=5时,(x2-x)-(x2-2x+1)等于
( )
A.-14
B.4
C.-4
D.1
7.小李编写了一段计算机程序,输入任意一个有理数,显示屏的结果总等于所输入有理数的平方与-2之和,当输入-3时,将所显示的结果再次输入,这时显示的结果应该是
( )
A.7
B.9
C.47
D.49
8.如1,为做一个试管架,在a
cm长的木条上钻了4个圆孔,每个圆孔的直径为2
cm,则x等于
( )
1
A.
cm
B.
cm
C.
cm
D.
cm
9.2是按照一定规律画出的“树形图”,经观察可以发现:图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”……照此规律,图A6比图A2多出“树枝”
( )
2
A.32个
B.56个
C.60个
D.64个
二、填空题(每小题4分,共24分)
10.单项式-的系数是 ,次数是 .?
11.如果-7+4ym+1-3y是三次三项式,那么m= .?
12.将多项式3x2-1-6x5-4x3按字母x的降幂排列为 .?
13.若单项式3xym与-xny2的和仍是单项式,则m+n的值是 .?
14.一个两位数,十位上的数字为x,个位上的数字比十位上的数字大3,则这个两位数可表示为 .?
15.观察下列等式:
12=1=×1×2×(2+1);
12+22=×2×3×(4+1);
12+22+32=×3×4×(6+1);
12+22+32+42=×4×5×(8+1);
…
可以推测12+22+32+…+n2=
.?
三、解答题(共49分)
16.(6分)计算:5(x+y)-3(2x-3y)-2(3x+2y).
17.(7分)先化简,再求值:已知x2-(2x2-4y)+2(x2-y),其中x=-1,y=.
18.(7分)小明在解数学题时,由于粗心,把原题“两个多项式A和B,其中B=4x2-5x-6,试求A+B”中的“A+B”错误地看成“A-B”,结果求出的答案是-7x2+10x+12,请你帮他算出A+B的正确答案.
19.(8分)已知A=x2+ax,B=2bx2-4x-1,且多项式2A+B的值与字母x的取值无关,求a,b的值.
20.(10分)老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,如3:
3
(1)求所捂住的多项式;
(2)若x为正整数,任取x的几个值并求出所捂住多项式的值,你能发现什么规律?
(3)若所捂住多项式的值为144,请直接写出正整数x的值.
21.(11分)如4①,将一个边长为a的正方形纸片剪去两个小长方形,得到一个“”形图案,如图②所示,再将剪下的两个小长方形无缝隙、无重叠地拼接成一个新的长方形(如图③所示).
(1)这个新长方形的长和宽分别为 , ;(用含a,b的代数式表示)?
(2)若a=8x2+4x+1,b=-x2+3x-,求这个新长方形的周长;
(3)在(2)的条件下,当x=时,求这个新长方形的周长.
4
教师详解详析
【作者说卷】
本套试卷分三种题型:选择题、填空题和解答题,共21道题,其中易、中、难题之比为7∶2∶1.全面考查整式的加减各知识点,重点考查代数式的化简和求值.
1.D
2.C [解析]
所含字母相同,并且相同字母的指数也相同的项是同类项,且所有常数项都是同类项,只有C项中相同字母的指数不同,故不是同类项.
3.D [解析]
常数项是-2,不是2.
4.C
5.D
6.B
7.C
8.D
9.C [解析]
图A2比图A1多出2个“树枝”,图A3比图A2多出4个“树枝”,图A4比图A3多出8个“树枝”……图A6比图A2多出“树枝”4+8+16+32=60(个).故选C.
10.- 3
11.2 [解析]
由题意知m+1=3,所以m=2.
12.-6x5-4x3+3x2-1
13.3 [解析]
由题意,得m=2,n=1,所以m+n=2+1=3.
14.11x+3 [解析]
十位上的数字是x,代表有x个10,个数上的数字是x+3,代表有x+3个1,故这个两位数是10x+(x+3)=11x+3.
15.n(n+1)(2n+1)
16.[解析]
先按照去括号法则去掉整式中的小括号,再合并整式中的同类项即可.
解:5(x+y)-3(2x-3y)-2(3x+2y)
=5x+5y-6x+9y-6x-4y
=-7x+10y.
17.解:原式=x2-2x2+4y+2x2-2y=x2+2y.
当x=-1,y=时,原式=1+1=2.
18.解:A+B=A-B+2B=(-7x2+10x+12)+2(4x2-5x-6)=x2.
19.解:因为A=x2+ax,B=2bx2-4x-1,
所以2A+B=2(x2+ax)+(2bx2-4x-1)
=2x2+2ax+2bx2-4x-1
=(2+2b)x2+(2a-4)x-1.
由结果与字母x的取值无关,
得2+2b=0,2a-4=0,解得a=2,b=-1.
20.解:(1)(-2x2+3x-6)-(-3x2+5x-7)
=-2x2+3x-6+3x2-5x+7
=x2-2x+1,
即所捂住的多项式是x2-2x+1.
(2)当x=1时,x2-2x+1=1-2+1=0;
当x=2时,x2-2x+1=4-4+1=1;
当x=3时,x2-2x+1=9-6+1=4;
当x=4时,x2-2x+1=16-8+1=9.
规律:所捂住多项式的值是代入的正整数x与1的差的平方.
(3)若所捂住多项式的值为144,则正整数x的值是13.
21.解:(1)由图可得,这个新长方形的长为(a-b)+(a-2b)=2a-3b,宽为(a-3b)×=a-b.
故答案为2a-3b,a-b.
(2)新长方形的周长是2a-3b+a-b×2=-×2=5a-9b.
当a=8x2+4x+1,b=-x2+3x-时,5a-9b=5(8x2+4x+1)-9-x2+3x-=40x2+20x+5+9x2-27x+=49x2-7x+.
(3)当x=时,49x2-7x+=49×2-7×+=-+=.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
