人教版八年级数学上册 12.2三角形全等的判定(SAS)同步练习(Word版,有答案)
文档属性
| 名称 | 人教版八年级数学上册 12.2三角形全等的判定(SAS)同步练习(Word版,有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 623.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 00:00:00 | ||
图片预览


文档简介
12.2三角形全等的判定(SAS)
一、单选题
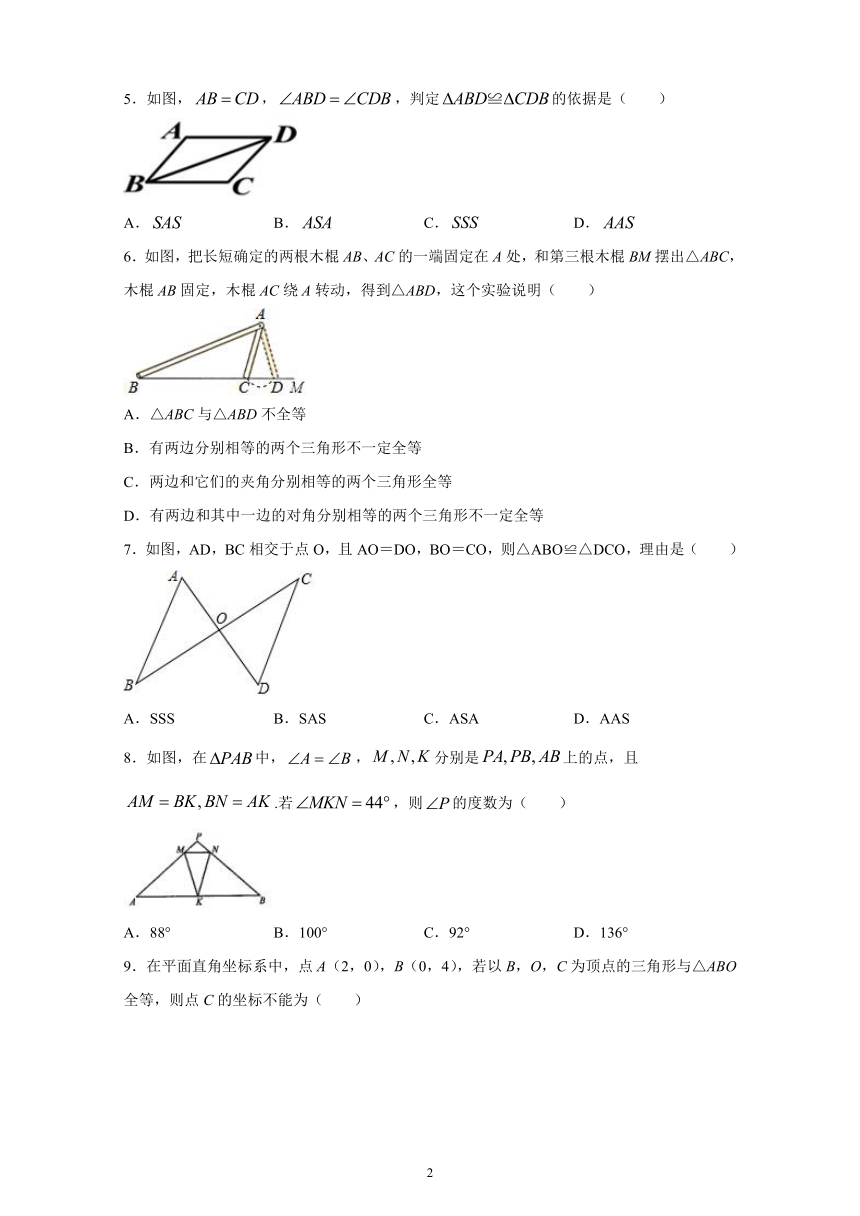
1.一块三角形玻璃被小红碰碎成四块,如图,小红打算只带其中的两块去玻璃店并买回一块和以前一样的玻璃,她需要( )
A.带其中的任意两块
B.带1,4或3,4就可以了
C.带1,4或2,4就可以了
D.带1,4或2,4或3,4均可
2.如图所示,表示两根长度相同的木条,若是的中点,经测量,则容器的内径为(
)
A.
B.
C.
D.
3.如图,两车从南北方向的路段的端出发,分别向东、向西行进相同的距离到达两地,若与的距离为千米,则与的距离为(
)
A.千米
B.千米
C.千米
D.无法确定
4.如图,在△ABC中,AB=AC,BE,
CF是中线,判定△AFC≌△AEB的方法是(
)
A.SSS
B.SAS
C.AAS
D.HL
5.如图,,,判定的依据是(
)
A.
B.
C.
D.
6.如图,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明( )
A.△ABC与△ABD不全等
B.有两边分别相等的两个三角形不一定全等
C.两边和它们的夹角分别相等的两个三角形全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
7.如图,AD,BC相交于点O,且AO=DO,BO=CO,则△ABO≌△DCO,理由是( )
A.SSS
B.SAS
C.ASA
D.AAS
8.如图,在中,,分别是上的点,且.若,则的度数为(
)
A.88°
B.100°
C.92°
D.136°
9.在平面直角坐标系中,点A(2,0),B(0,4),若以B,O,C为顶点的三角形与△ABO全等,则点C的坐标不能为( )
A.(0,﹣4)
B.(﹣2,0)
C.(2,4)
D.(﹣2,4)
10.如图,AB=AC,AD=AE,∠BAC=∠DAE,
∠1=25°,
∠2=30°,则∠3的度数是(
)
A.45°
B.50°
C.55°
D.60°
11.如图,已知方格纸中是4个相同的小正方形,则的度数为(
)
A.
B.
C.
D.
12.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( )
A.7
B.5
C.3
D.2
二、填空题
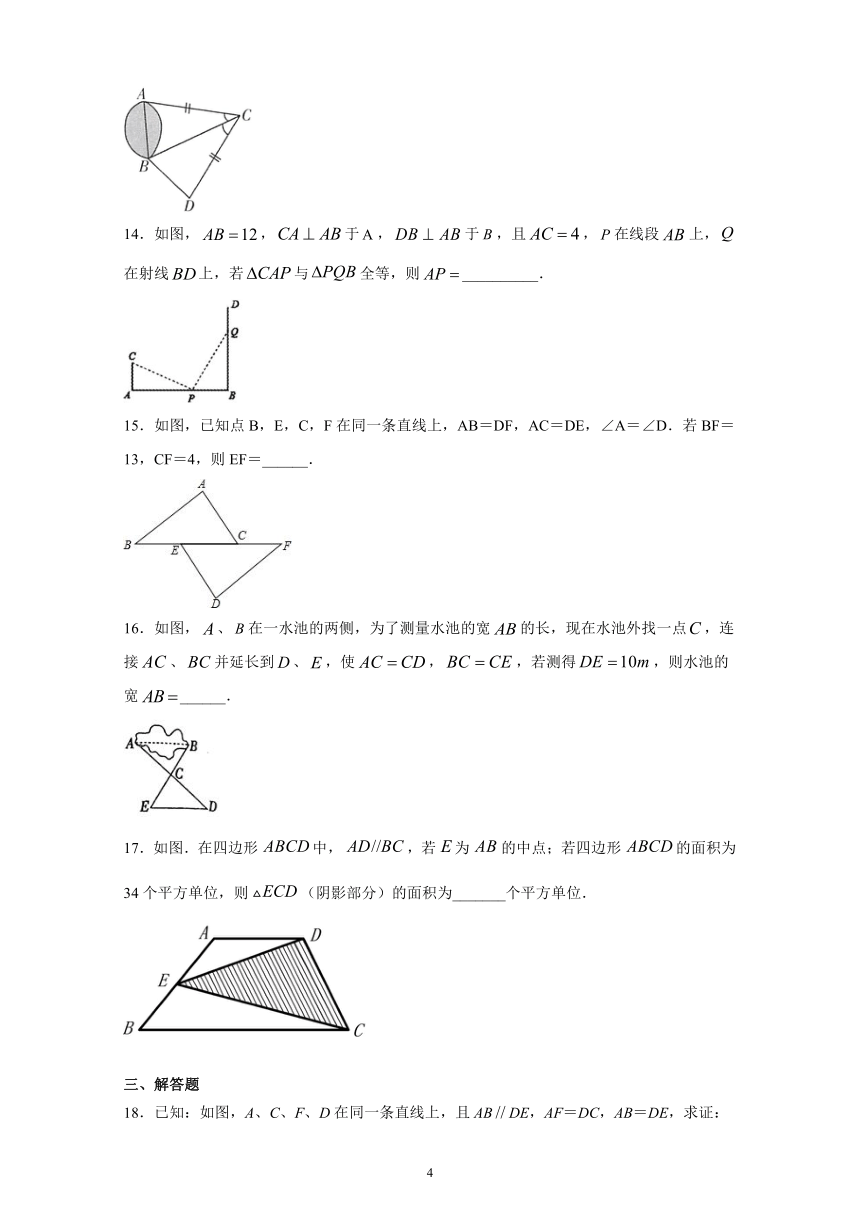
13.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,采用了如图所示的这种方法,利用了证三角形全等中的________.
14.如图,,于,于,且,在线段上,在射线上,若与全等,则__________.
15.如图,已知点B,E,C,F在同一条直线上,AB=DF,AC=DE,∠A=∠D.若BF=13,CF=4,则EF=______.
16.如图,、在一水池的两侧,为了测量水池的宽的长,现在水池外找一点,连接、并延长到、,使,,若测得,则水池的宽______.
17.如图.在四边形中,,若为的中点;若四边形的面积为34个平方单位,则(阴影部分)的面积为_______个平方单位.
三、解答题
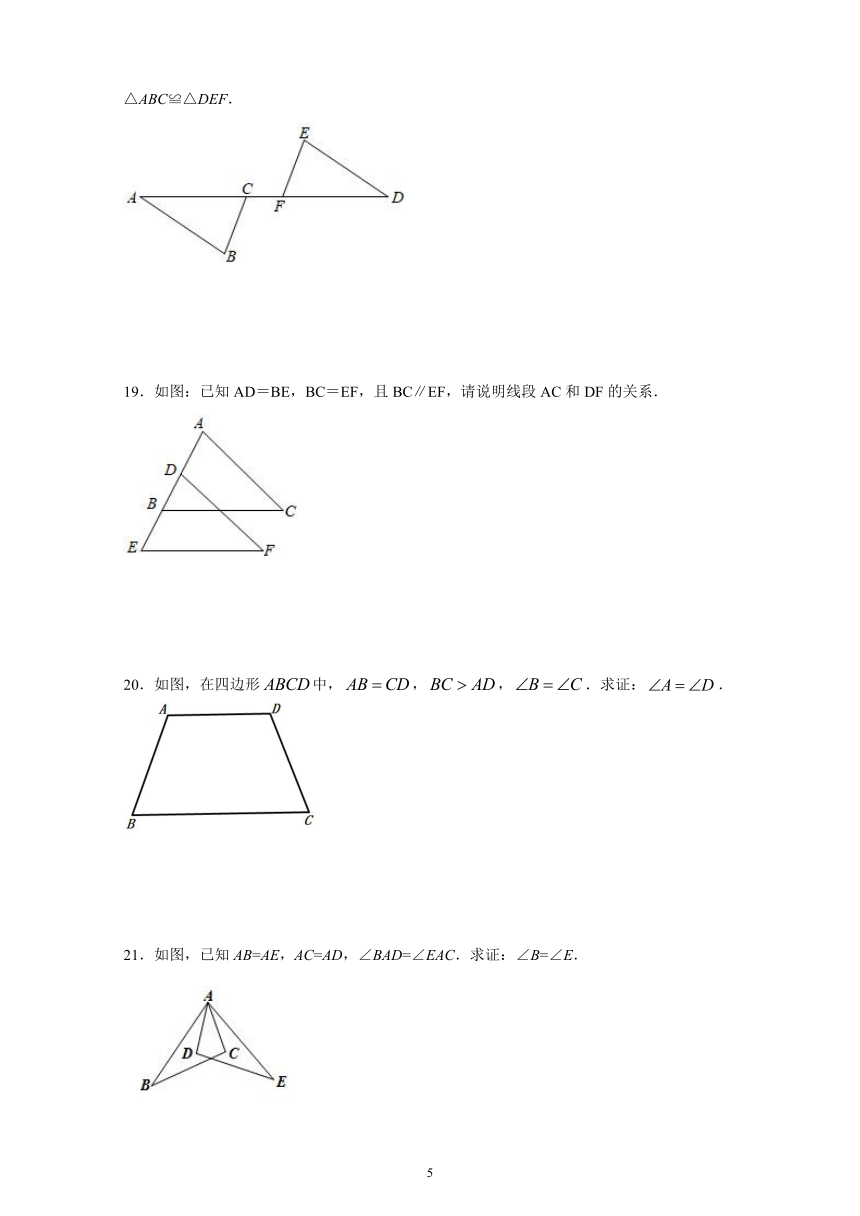
18.已知:如图,A、C、F、D在同一条直线上,且ABDE,AF=DC,AB=DE,求证:△ABC≌△DEF.
19.如图:已知AD=BE,BC=EF,且BC∥EF,请说明线段AC和DF的关系.
20.如图,在四边形中,,,.求证:.
21.如图,已知AB=AE,AC=AD,∠BAD=∠EAC.求证:∠B=∠E.
22.已知:如图,E为BC上一点,AC∥BD.AC=BE.BC=BD.求证:AB=DE.
23.如图,已知平分,.求证,.
24.如图,在四边形ABCD中,,点E为对角线BD上一点,,且.
(1)求证:;
(2)若,求的度数.
参考答案
1.D
解:由图可知,带上1和4相当于有两个角和一条边,所以可得两块三角形玻璃全等;同理,带上3和4也相当于有两角夹一边,同样也可以得三角形全等;2和4中,4确定了上边的角的大小及两边的方向,2又确定了底边的方向,继而可得全等;
故选:D
2.B
解:∵O是AA′、BB′的中点,AA′=BB′,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,,
∴△AOB≌△A′OB′,
∴A′B′=AB=9cm.
故选:B.
3.A
解:由题意得:AC=AD,,
∴在和中
∴
∴
∴与的距离为千米故选:A.
4.B
解:∵BE、CF是中线,
∴AE=AC,AF=AB,
∵AB=AC,
∴AF=AE,
在△AFC和△AEB中,
,
∴△AFC≌△AEB(SAS),
故选:B.
5.A
解:在和中
所以(SAS)
故选:A
6.D
解:由题意可知:AB=AB,AC=AD,∠ABC=∠ABD,
满足有两边和其中一边的对角分别相等,但是△ABC与△ABD不全等,
故选:D.
7.B
解:∵OA=OD,∠AOB=∠COD,OB=OC,
∴△ABO≌△DCO(SAS).
故选:B.
8.C
解:在△MAK和△KBN中,
,
∴△MAK≌△KBN(SAS),
∴∠AMK=∠BKN,
∵∠MKN=44,
∴∠AKM+∠BKN=180-∠MKN=136,
∴∠AKM+∠AMK=136,
∴∠A=180-136=44,
∵∠P+∠A+∠B=180,
∴∠P=92.
故此题选择C.
9.A
解:如图所示:
∵A(2,0),B(0,4)
∴OA=2,OB=4,∠AOB=90°
当C1坐标为(0,﹣4)时,B、O、C1同一条直线上,不能构成三角形,故选A;
当C2坐标为(﹣2,0)时,OC2=
OA=2,∠C2O
B
=∠AOB=90°,OB=OB
∴△C2O
B≌△AOB,故不选B;
当C3坐标为(2,4)时,BC3=
OA=2,∠C3
B
O
=∠AOB=90°,OB=BO
∴△C3BO≌△AOB,故不选C;
当C4坐标为(﹣2,4)时,BC4=
OA=2,∠C4BO
=∠AOB=90°,OB=BO
∴△C4BO≌△AOB,故不选D.
故选A.
10.C
解:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠1=∠CAE.
在△ADB和AEC中,
,
∴△ADB≌AEC(SAS),
∴∠ABD=∠2=30°.
∵∠3=∠1+∠ABD.
∴∠3=25°+30°=55°.
故选C.
11.D
解:∵在△ABC和△AED中,
,
∴△ABC≌△AED(SAS),
∴∠1=∠AED,
∵∠AED+∠2=90°,
∴∠1+∠2=90°,
故选:D.
12.B
解:∵AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,
∴Rt△AEC≌Rt△CDB
又∵AE=7,BD=2,
∴CE=BD=2,AE=CD=7,
DE=CD-CE=7-2=5.
13.SAS
解:观察图形发现:,,,
所以利用了证三角形全等中的SAS(或边角边).
故答案为:SAS.
14.6或8
解:∵于,于
∴
当,,时,与全等,此时;
当,,时,与全等,此时;
故答案为:6或8.
15.9
解:根据题意
得:(SAS)
∴
∵
∴
故答案为9
16.10m
解:如图,在△ACB和△DCE中
∵
(SAS),
∴,
∴.
故答案为:10m.
17.17.
解:如图:
延长DE交直线CB于点F,
E为AB中点,,
在和中,
;
四边形的面积=面积=34;
FE=DE,E为DF中线,和同高,底边是一半,
.
故答案为:17
18.见解析
证明:∵AB∥DE,
∴∠A=∠D,
∵AF=CD,
∴AD+CF=CF+DF,
∴AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
19.相等且平行
解:AC与DF的关系是相等且平行,
理由:∵AD=BE,
∴AD+DB=BE+DB,
∴AB=DE,
∵BC∥EF,
∴∠ABC=∠DEF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DE,∠A=∠EDF,
∴AC∥DF,
即AC与DF的关系是相等且平行.
20.证明见解析.
解:连接,BD
在与中,,
∴,
,
在与中,,
∴,
∴.
21.证明见解析.
证明:∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC,
∴∠BAC=∠EAD,
在与中,
,
∴(SAS),
∴∠B=∠E.
22.详见解析
证明:∵AC∥BD,
∴∠ACB=∠DBC,
∵AC=BE,BC=BD,
∴△ABC≌△EDB,
∴AB=DE.
23.见解析.
证明:
AC平分,
,
在与中
(SAS).
24.(1)证明见解析;(2)
解:(1)∵,
∴,
在△ADB和△EBC中,
,
∴△ADB≌△EBC,
∴,
∴,
∴;
(2)∵△ADB≌△EBC,
∴,
∴,
∵,
∴,
∴.
一、单选题
1.一块三角形玻璃被小红碰碎成四块,如图,小红打算只带其中的两块去玻璃店并买回一块和以前一样的玻璃,她需要( )
A.带其中的任意两块
B.带1,4或3,4就可以了
C.带1,4或2,4就可以了
D.带1,4或2,4或3,4均可
2.如图所示,表示两根长度相同的木条,若是的中点,经测量,则容器的内径为(
)
A.
B.
C.
D.
3.如图,两车从南北方向的路段的端出发,分别向东、向西行进相同的距离到达两地,若与的距离为千米,则与的距离为(
)
A.千米
B.千米
C.千米
D.无法确定
4.如图,在△ABC中,AB=AC,BE,
CF是中线,判定△AFC≌△AEB的方法是(
)
A.SSS
B.SAS
C.AAS
D.HL
5.如图,,,判定的依据是(
)
A.
B.
C.
D.
6.如图,把长短确定的两根木棍AB、AC的一端固定在A处,和第三根木棍BM摆出△ABC,木棍AB固定,木棍AC绕A转动,得到△ABD,这个实验说明( )
A.△ABC与△ABD不全等
B.有两边分别相等的两个三角形不一定全等
C.两边和它们的夹角分别相等的两个三角形全等
D.有两边和其中一边的对角分别相等的两个三角形不一定全等
7.如图,AD,BC相交于点O,且AO=DO,BO=CO,则△ABO≌△DCO,理由是( )
A.SSS
B.SAS
C.ASA
D.AAS
8.如图,在中,,分别是上的点,且.若,则的度数为(
)
A.88°
B.100°
C.92°
D.136°
9.在平面直角坐标系中,点A(2,0),B(0,4),若以B,O,C为顶点的三角形与△ABO全等,则点C的坐标不能为( )
A.(0,﹣4)
B.(﹣2,0)
C.(2,4)
D.(﹣2,4)
10.如图,AB=AC,AD=AE,∠BAC=∠DAE,
∠1=25°,
∠2=30°,则∠3的度数是(
)
A.45°
B.50°
C.55°
D.60°
11.如图,已知方格纸中是4个相同的小正方形,则的度数为(
)
A.
B.
C.
D.
12.如图,AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,AE=7,BD=2,则DE的长是( )
A.7
B.5
C.3
D.2
二、填空题
13.如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,采用了如图所示的这种方法,利用了证三角形全等中的________.
14.如图,,于,于,且,在线段上,在射线上,若与全等,则__________.
15.如图,已知点B,E,C,F在同一条直线上,AB=DF,AC=DE,∠A=∠D.若BF=13,CF=4,则EF=______.
16.如图,、在一水池的两侧,为了测量水池的宽的长,现在水池外找一点,连接、并延长到、,使,,若测得,则水池的宽______.
17.如图.在四边形中,,若为的中点;若四边形的面积为34个平方单位,则(阴影部分)的面积为_______个平方单位.
三、解答题
18.已知:如图,A、C、F、D在同一条直线上,且ABDE,AF=DC,AB=DE,求证:△ABC≌△DEF.
19.如图:已知AD=BE,BC=EF,且BC∥EF,请说明线段AC和DF的关系.
20.如图,在四边形中,,,.求证:.
21.如图,已知AB=AE,AC=AD,∠BAD=∠EAC.求证:∠B=∠E.
22.已知:如图,E为BC上一点,AC∥BD.AC=BE.BC=BD.求证:AB=DE.
23.如图,已知平分,.求证,.
24.如图,在四边形ABCD中,,点E为对角线BD上一点,,且.
(1)求证:;
(2)若,求的度数.
参考答案
1.D
解:由图可知,带上1和4相当于有两个角和一条边,所以可得两块三角形玻璃全等;同理,带上3和4也相当于有两角夹一边,同样也可以得三角形全等;2和4中,4确定了上边的角的大小及两边的方向,2又确定了底边的方向,继而可得全等;
故选:D
2.B
解:∵O是AA′、BB′的中点,AA′=BB′,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,,
∴△AOB≌△A′OB′,
∴A′B′=AB=9cm.
故选:B.
3.A
解:由题意得:AC=AD,,
∴在和中
∴
∴
∴与的距离为千米故选:A.
4.B
解:∵BE、CF是中线,
∴AE=AC,AF=AB,
∵AB=AC,
∴AF=AE,
在△AFC和△AEB中,
,
∴△AFC≌△AEB(SAS),
故选:B.
5.A
解:在和中
所以(SAS)
故选:A
6.D
解:由题意可知:AB=AB,AC=AD,∠ABC=∠ABD,
满足有两边和其中一边的对角分别相等,但是△ABC与△ABD不全等,
故选:D.
7.B
解:∵OA=OD,∠AOB=∠COD,OB=OC,
∴△ABO≌△DCO(SAS).
故选:B.
8.C
解:在△MAK和△KBN中,
,
∴△MAK≌△KBN(SAS),
∴∠AMK=∠BKN,
∵∠MKN=44,
∴∠AKM+∠BKN=180-∠MKN=136,
∴∠AKM+∠AMK=136,
∴∠A=180-136=44,
∵∠P+∠A+∠B=180,
∴∠P=92.
故此题选择C.
9.A
解:如图所示:
∵A(2,0),B(0,4)
∴OA=2,OB=4,∠AOB=90°
当C1坐标为(0,﹣4)时,B、O、C1同一条直线上,不能构成三角形,故选A;
当C2坐标为(﹣2,0)时,OC2=
OA=2,∠C2O
B
=∠AOB=90°,OB=OB
∴△C2O
B≌△AOB,故不选B;
当C3坐标为(2,4)时,BC3=
OA=2,∠C3
B
O
=∠AOB=90°,OB=BO
∴△C3BO≌△AOB,故不选C;
当C4坐标为(﹣2,4)时,BC4=
OA=2,∠C4BO
=∠AOB=90°,OB=BO
∴△C4BO≌△AOB,故不选D.
故选A.
10.C
解:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠1=∠CAE.
在△ADB和AEC中,
,
∴△ADB≌AEC(SAS),
∴∠ABD=∠2=30°.
∵∠3=∠1+∠ABD.
∴∠3=25°+30°=55°.
故选C.
11.D
解:∵在△ABC和△AED中,
,
∴△ABC≌△AED(SAS),
∴∠1=∠AED,
∵∠AED+∠2=90°,
∴∠1+∠2=90°,
故选:D.
12.B
解:∵AC=BC,AE=CD,AE⊥CE于点E,BD⊥CD于点D,
∴Rt△AEC≌Rt△CDB
又∵AE=7,BD=2,
∴CE=BD=2,AE=CD=7,
DE=CD-CE=7-2=5.
13.SAS
解:观察图形发现:,,,
所以利用了证三角形全等中的SAS(或边角边).
故答案为:SAS.
14.6或8
解:∵于,于
∴
当,,时,与全等,此时;
当,,时,与全等,此时;
故答案为:6或8.
15.9
解:根据题意
得:(SAS)
∴
∵
∴
故答案为9
16.10m
解:如图,在△ACB和△DCE中
∵
(SAS),
∴,
∴.
故答案为:10m.
17.17.
解:如图:
延长DE交直线CB于点F,
E为AB中点,,
在和中,
;
四边形的面积=面积=34;
FE=DE,E为DF中线,和同高,底边是一半,
.
故答案为:17
18.见解析
证明:∵AB∥DE,
∴∠A=∠D,
∵AF=CD,
∴AD+CF=CF+DF,
∴AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
19.相等且平行
解:AC与DF的关系是相等且平行,
理由:∵AD=BE,
∴AD+DB=BE+DB,
∴AB=DE,
∵BC∥EF,
∴∠ABC=∠DEF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴AC=DE,∠A=∠EDF,
∴AC∥DF,
即AC与DF的关系是相等且平行.
20.证明见解析.
解:连接,BD
在与中,,
∴,
,
在与中,,
∴,
∴.
21.证明见解析.
证明:∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC,
∴∠BAC=∠EAD,
在与中,
,
∴(SAS),
∴∠B=∠E.
22.详见解析
证明:∵AC∥BD,
∴∠ACB=∠DBC,
∵AC=BE,BC=BD,
∴△ABC≌△EDB,
∴AB=DE.
23.见解析.
证明:
AC平分,
,
在与中
(SAS).
24.(1)证明见解析;(2)
解:(1)∵,
∴,
在△ADB和△EBC中,
,
∴△ADB≌△EBC,
∴,
∴,
∴;
(2)∵△ADB≌△EBC,
∴,
∴,
∵,
∴,
∴.
