全等三角形及其判定习题课
文档属性
| 名称 | 全等三角形及其判定习题课 |

|
|
| 格式 | zip | ||
| 文件大小 | 847.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-18 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
题目设置:
竞赛题由一、必答题;二、选答题;三、共答题;四、抢答题四部分组成。
规则:共18道题。
1、必答题:每组必须完成此题,答对加分。答错不加分,但此题分数由答对题组平分。
2、选答题:每组必须完成此题,答对加分,答错不加分,但此题分数由答对题组平分。
3、共答题:各组共答一题,答错不加分,但此题分数分别加给答对此题的组。
4、抢答题:此题采用抢答方式进行,优先抢到题者优先作答。答对加分,答错扣分,扣除的分数分别加给答对此题的组。
1、①全等三角形的概念:
能完全重合的两个三角形叫做全等三角形。
②全等三角形的特征:
全等三角形的对应边相等,对应角相等。
4分
4分
2、三角形全等的条件:
①_________对应相等的两个三角形全等(简写成“边边边”或“SSS”);
②两角和__________________对应相等的两个三角形全等.(简写成__________或“_________”)
③ 两角和__________________对应相等的两个三角形全等.(简写成________或“ASA”)
④ 两边和_______________对应相等的两个三角形全等(简写成“边角边”或“________”);
三边
它们的夹边
角边角
ASA
其中一个角的对边
角角边
它们的的夹角
SAS
4分
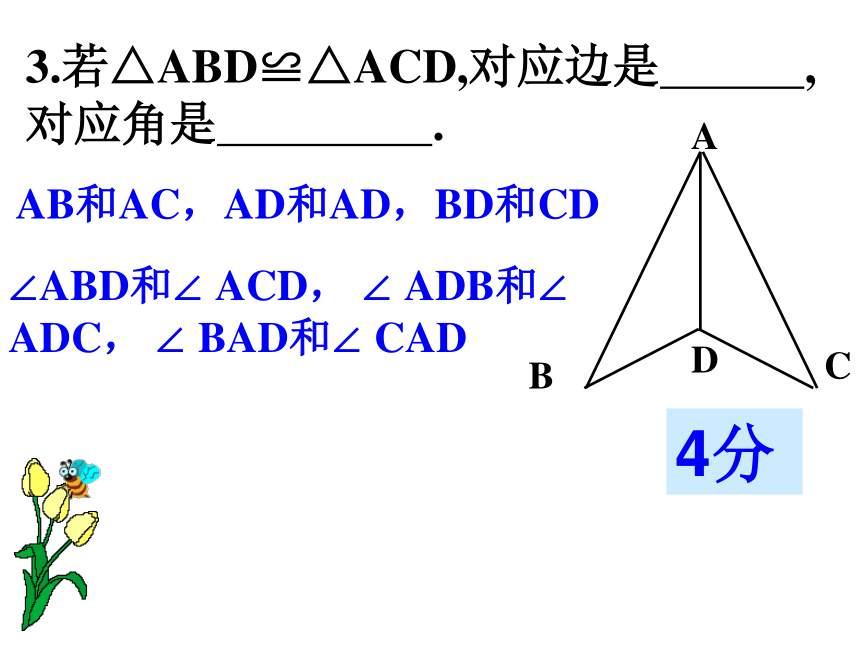
3.若△ABD≌△ACD,对应边是 ,对应角是 .
A
B
C
D
AB和AC,AD和AD,BD和CD
∠ABD和∠ ACD, ∠ ADB和∠ ADC, ∠ BAD和∠ CAD
4分
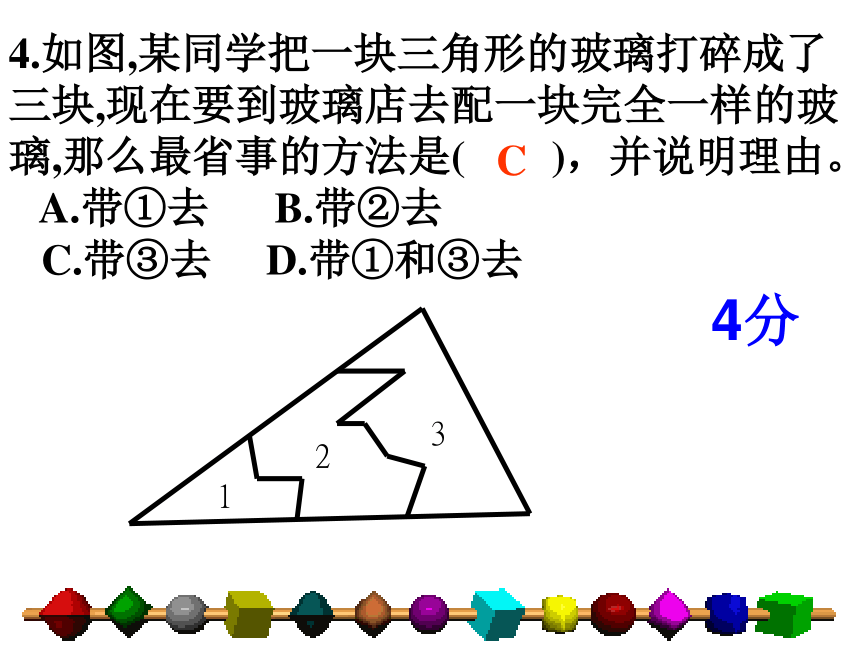
4.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( ),并说明理由。
A.带①去 B.带②去
C.带③去 D.带①和③去
C
5.在下列说法中,正确的有( )个.并说明判断的理由。
①三角对应相等的两个三角形全等
②三边对应相等的两个三角形全等
③两角、一边对应相等的两个三角形全等
④两边、一角对应相等的两个三角形全等
A.1 B.2 C.3 D.4
B
4分
1
2
3
4
5
4分
1.如图,已知△ABC和△DCB中,AB=DC,请补充一个条件 ,使△ABC≌ △DCB.
A
B
C
D
思路:
找夹角
找第三边
已知两边:
∠ABC=∠DCB (SAS)
AC=DB (SSS)
4分
2.如图,已知∠C=∠D,要识别△ABC≌△ABD, 需要添加的一个条件是 .
A
C
B
D
思路
找任一角
已知一边一角
(边与角相对)
(AAS)
∠CAB=∠DAB
或者∠CBA=∠DBA
3.如图,已知∠1=∠2,要识别△ABC≌△CDA, 需要添加的一个条件是 .
4分
思路:
已知一边一角 (边与角相邻):
A
B
C
D
2
1
找夹这个角的另一边
找夹这条边的另一角
找边的对角
AD=CB
∠ACD=∠CAB
∠D=∠B
(SAS)
(ASA)
(AAS)
4.如图,已知∠B=∠E,要识别△ABC≌ △AED,需要添加的一个条件是 .
思路:
已知两角:
找夹边
找一角的对边
A
B
C
D
E
AB=AE
AC=AD
或DE=BC
(ASA)
(AAS)
4分
5.如图,AM=AN, BM=BN
请说明△AMB≌△ANB的理由
解:在△AMB和△ANB中
∴ ≌ ( )
AN
已知
BM
AB
AB
△ABM
△ABN
SSS
4分
1.如图, 已知直线AD, BC交于点E, 且AE=BE, 欲说明△AEC≌△BED,需增加的条件可以是______________________(只填一个即可).
解: 根据“SAS”, 可添加CE=DE; 根据“ASA”,可添加∠A=∠B; 根据“AAS”, 可添加∠C=∠D.
故填CE=DE或∠A=∠B或∠C=∠D.
4分
2.如图, 已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,可补充的条件是 _____________________(写出一个即可).
解:可补充的条件是: 当AC=AE,△ABC≌△ADE(SAS); 当∠C=∠E,△ABC≌△ADE(AAS); 当∠B=∠D,△ABC≌△ADE(ASA). 故答案为:AC=AE或∠C=∠E或∠B=∠D.
4分
3.如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP (不能添加辅助线),你增加的条件是 .
解:添加的条件为BP=DP或AB=CD或∠A=∠C或∠B=∠D或AB//CD.
4分
4.如图,沿AM折叠,使D点落在BC上的N点处,如果AD=7cm, DM=5cm,∠DAM=300,则AN= cm, NM=___cm, ∠NAM= .
A
B
C
D
M
N
7
5
300
4分
5.如图,AB=AC,∠B=∠C,你能证明△ABD≌△ACE吗?
A
B
C
D
E
4分
证明:在△ABD≌△ACE中
∠A=∠A,
AB=AC,
∠B=∠C,
∴△ABD≌△ACE(ASA).
∵
1
2
3
1.已知:如图,BD=CD,∠ABD=∠ACD,DE、DF分别垂直于AB及AC交延长线于E、F. 求证:DE=DF.
证明: ∵∠ABD=∠ACD ∴∠EBD=∠FCD
∵BD=CD(已知),∠E=∠F=90° ∴△BDE≌△CDF(AAS) ∴DE=DF
8分
2.如图,AC和BD相交于点O,AB=DC,∠A=∠D,
(1)请写出符合条件的五个结论(对顶角除外,且不添加辅助线)
(2)从你写出的五个结论中任选一个说明你的理由.
O
B
C
A
D
10分
解: (1)答:符合上述条件的五个结论为:△AOB≌△DOC,OA=OD,OB=OC,∠ABO=∠DCO,∠OBC=∠OCB. (2) 证明如下: ∵AB=DC,∠A=∠D, 又有∠AOB=∠DOC ∴△AOB≌△DOC ∴OA=OD,OB=OC,∠ABO=∠DCO ∵OB=OC ∴∠OBC=∠OCB.
3.已知:如图,AB=AE,AC=AD , BC=DE, C , D在BE边上.
求证:∠CAE=∠DAB.
8分
3.证明:∵AB=AC, ∴∠ABC=∠ACB. ∴∠ABD=∠ACE. ∵CD=BE,CD=DB+BC,BE=CE+BC, ∴DB=CE. ∵AB=AC,∠ABD=∠ACE,DB=CE, ∴△ABD≌△ACE. ∴AD=AE.
题目设置:
竞赛题由一、必答题;二、选答题;三、共答题;四、抢答题四部分组成。
规则:共18道题。
1、必答题:每组必须完成此题,答对加分。答错不加分,但此题分数由答对题组平分。
2、选答题:每组必须完成此题,答对加分,答错不加分,但此题分数由答对题组平分。
3、共答题:各组共答一题,答错不加分,但此题分数分别加给答对此题的组。
4、抢答题:此题采用抢答方式进行,优先抢到题者优先作答。答对加分,答错扣分,扣除的分数分别加给答对此题的组。
1、①全等三角形的概念:
能完全重合的两个三角形叫做全等三角形。
②全等三角形的特征:
全等三角形的对应边相等,对应角相等。
4分
4分
2、三角形全等的条件:
①_________对应相等的两个三角形全等(简写成“边边边”或“SSS”);
②两角和__________________对应相等的两个三角形全等.(简写成__________或“_________”)
③ 两角和__________________对应相等的两个三角形全等.(简写成________或“ASA”)
④ 两边和_______________对应相等的两个三角形全等(简写成“边角边”或“________”);
三边
它们的夹边
角边角
ASA
其中一个角的对边
角角边
它们的的夹角
SAS
4分
3.若△ABD≌△ACD,对应边是 ,对应角是 .
A
B
C
D
AB和AC,AD和AD,BD和CD
∠ABD和∠ ACD, ∠ ADB和∠ ADC, ∠ BAD和∠ CAD
4分
4.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( ),并说明理由。
A.带①去 B.带②去
C.带③去 D.带①和③去
C
5.在下列说法中,正确的有( )个.并说明判断的理由。
①三角对应相等的两个三角形全等
②三边对应相等的两个三角形全等
③两角、一边对应相等的两个三角形全等
④两边、一角对应相等的两个三角形全等
A.1 B.2 C.3 D.4
B
4分
1
2
3
4
5
4分
1.如图,已知△ABC和△DCB中,AB=DC,请补充一个条件 ,使△ABC≌ △DCB.
A
B
C
D
思路:
找夹角
找第三边
已知两边:
∠ABC=∠DCB (SAS)
AC=DB (SSS)
4分
2.如图,已知∠C=∠D,要识别△ABC≌△ABD, 需要添加的一个条件是 .
A
C
B
D
思路
找任一角
已知一边一角
(边与角相对)
(AAS)
∠CAB=∠DAB
或者∠CBA=∠DBA
3.如图,已知∠1=∠2,要识别△ABC≌△CDA, 需要添加的一个条件是 .
4分
思路:
已知一边一角 (边与角相邻):
A
B
C
D
2
1
找夹这个角的另一边
找夹这条边的另一角
找边的对角
AD=CB
∠ACD=∠CAB
∠D=∠B
(SAS)
(ASA)
(AAS)
4.如图,已知∠B=∠E,要识别△ABC≌ △AED,需要添加的一个条件是 .
思路:
已知两角:
找夹边
找一角的对边
A
B
C
D
E
AB=AE
AC=AD
或DE=BC
(ASA)
(AAS)
4分
5.如图,AM=AN, BM=BN
请说明△AMB≌△ANB的理由
解:在△AMB和△ANB中
∴ ≌ ( )
AN
已知
BM
AB
AB
△ABM
△ABN
SSS
4分
1.如图, 已知直线AD, BC交于点E, 且AE=BE, 欲说明△AEC≌△BED,需增加的条件可以是______________________(只填一个即可).
解: 根据“SAS”, 可添加CE=DE; 根据“ASA”,可添加∠A=∠B; 根据“AAS”, 可添加∠C=∠D.
故填CE=DE或∠A=∠B或∠C=∠D.
4分
2.如图, 已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,可补充的条件是 _____________________(写出一个即可).
解:可补充的条件是: 当AC=AE,△ABC≌△ADE(SAS); 当∠C=∠E,△ABC≌△ADE(AAS); 当∠B=∠D,△ABC≌△ADE(ASA). 故答案为:AC=AE或∠C=∠E或∠B=∠D.
4分
3.如图,已知AC⊥BD于点P,AP=CP,请增加一个条件,使△ABP≌△CDP (不能添加辅助线),你增加的条件是 .
解:添加的条件为BP=DP或AB=CD或∠A=∠C或∠B=∠D或AB//CD.
4分
4.如图,沿AM折叠,使D点落在BC上的N点处,如果AD=7cm, DM=5cm,∠DAM=300,则AN= cm, NM=___cm, ∠NAM= .
A
B
C
D
M
N
7
5
300
4分
5.如图,AB=AC,∠B=∠C,你能证明△ABD≌△ACE吗?
A
B
C
D
E
4分
证明:在△ABD≌△ACE中
∠A=∠A,
AB=AC,
∠B=∠C,
∴△ABD≌△ACE(ASA).
∵
1
2
3
1.已知:如图,BD=CD,∠ABD=∠ACD,DE、DF分别垂直于AB及AC交延长线于E、F. 求证:DE=DF.
证明: ∵∠ABD=∠ACD ∴∠EBD=∠FCD
∵BD=CD(已知),∠E=∠F=90° ∴△BDE≌△CDF(AAS) ∴DE=DF
8分
2.如图,AC和BD相交于点O,AB=DC,∠A=∠D,
(1)请写出符合条件的五个结论(对顶角除外,且不添加辅助线)
(2)从你写出的五个结论中任选一个说明你的理由.
O
B
C
A
D
10分
解: (1)答:符合上述条件的五个结论为:△AOB≌△DOC,OA=OD,OB=OC,∠ABO=∠DCO,∠OBC=∠OCB. (2) 证明如下: ∵AB=DC,∠A=∠D, 又有∠AOB=∠DOC ∴△AOB≌△DOC ∴OA=OD,OB=OC,∠ABO=∠DCO ∵OB=OC ∴∠OBC=∠OCB.
3.已知:如图,AB=AE,AC=AD , BC=DE, C , D在BE边上.
求证:∠CAE=∠DAB.
8分
3.证明:∵AB=AC, ∴∠ABC=∠ACB. ∴∠ABD=∠ACE. ∵CD=BE,CD=DB+BC,BE=CE+BC, ∴DB=CE. ∵AB=AC,∠ABD=∠ACE,DB=CE, ∴△ABD≌△ACE. ∴AD=AE.
