人教版八年级数学上册 12.3角平分线的性质 同步练习(Word版,有答案)
文档属性
| 名称 | 人教版八年级数学上册 12.3角平分线的性质 同步练习(Word版,有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 577.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-22 00:00:00 | ||
图片预览




文档简介
12.3角平分线的性质
一、单选题
1.如图,,和分别平分和,过点,且与垂直.若,则点到的距离是( )
A.8
B.6
C.4
D.2
2.如图,平分平分,且,下列结论:①平分,②;③;④.其中正确的个数为(
)
A.4个
B.3个
C.2个
D.1个
3.如图,中,,利用尺规在,上分别截取,,使;分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线交于G.若.P为上一动点,则的最小值为(
)
A.无法确定
B.1
C.2
D.4
4.如图,在中,,平分,于E,则下列结论中,不正确的是(
)
A.平分
B.
C.平分
D.
5.一个角的平分线的尺规作法,其理论依据是全等三角形判定定理(
)
A.边角边
B.边边边
C.角角边
D.角边角
6.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9.6cm,则D到AB的距离为(
)
A.2.2cm
B.3.2cm
C.4.8cm
D.6.4cm
7.如图,在中,平分,且,则的面积是(
)
A.9
B.12
C.15
D.18
8.如图,,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E,F,再分别以点E、F为圆心,大于长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若,则的大小为(
)度.
A.8
B.16
C.32
D.64
9.如图,在△ABC中,∠C=90°,BC=1,AC=2,BD是∠ABC的平分线,设△ABD,△BCD的面积分别是S1,S2,则S1:S2等于( )
A.2:1
B.:1
C.3:2
D.2:
10.如图所示,点在的内部,,,垂足分别为,,,则与的大小关系是(
)
A.
B.
C.
D.无法确定
11.如图,在四边形ABCD中,∠A=∠BDC=90°,∠C=∠ADB,点P是BC边上的一动点,连接DP,若AD=4,则DP的长不可能是( )
A.6
B.5
C.4
D.3
12.如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠EFH;②2∠BEF=∠BAF+∠C;③(∠BAC-∠C);④∠BGH=∠ABE+∠C其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.①②③④
二、填空题
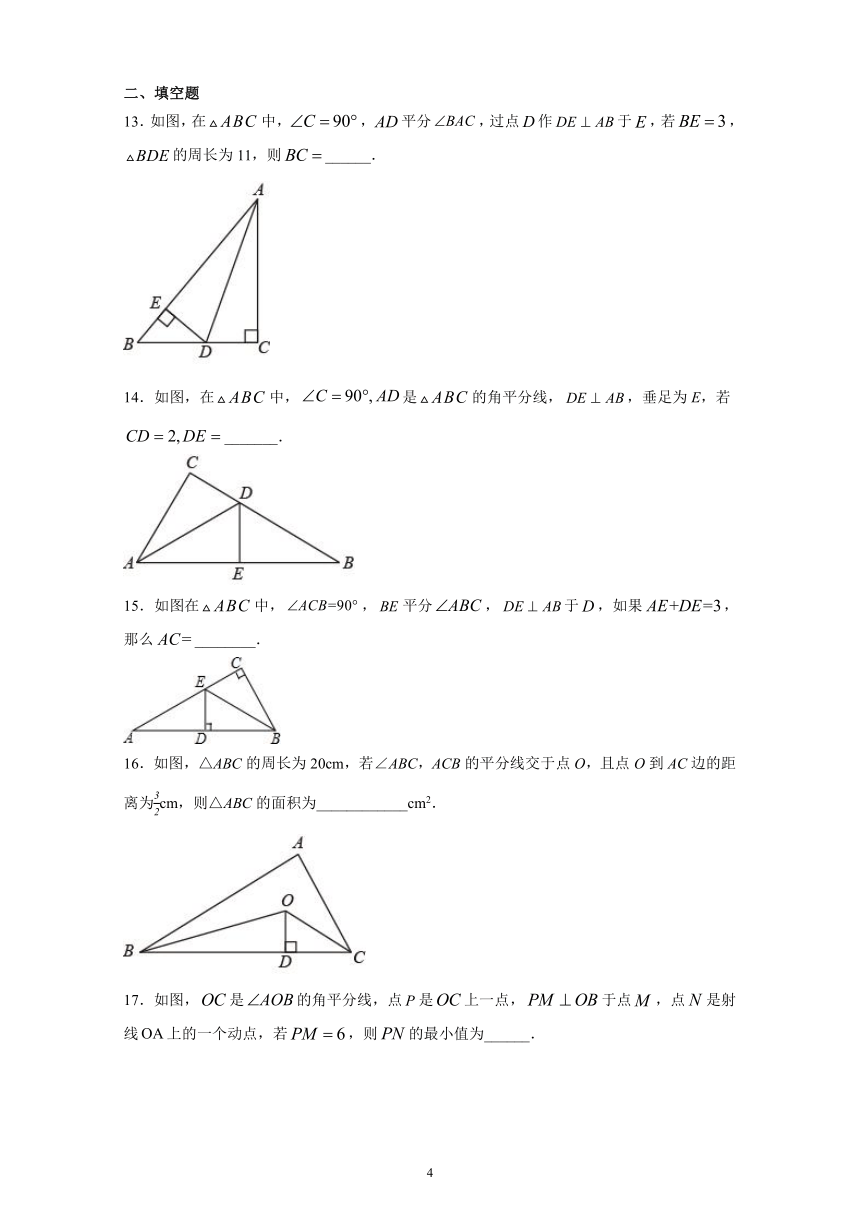
13.如图,在中,,平分,过点作于,若,的周长为11,则______.
14.如图,在中,是的角平分线,,垂足为E,若_______.
15.如图在中,,平分,于,如果,那么________.
16.如图,△ABC的周长为20cm,若∠ABC,ACB的平分线交于点O,且点O到AC边的距离为cm,则△ABC的面积为____________cm2.
17.如图,是的角平分线,点是上一点,于点,点是射线上的一个动点,若,则的最小值为______.
三、解答题
18.如图,已知∠ABC,求作:∠ABC的角平分线BP(不写作法,保留作图痕迹).
19.如图,,平分交于点.若,求的度数.
20.如图,的平分线与的外角平分线相交于点,连接.求证:是的外角平分线.
21.如图,在中,,点D在BC边上,连接AD,点E、F分别为AB边,AC边上的点,连接DE、DF,使得DA平分∠EDF,且DE=DF,过点D作DG⊥AB于点G.
(1)若DFAB,求证:AE=DE;
(2)求证:DG=CD.
22.如图,在中,平分交于点,,分别交,于点,.
(1)求证:;
(2)若,,求的度数.
23.如图,四边形中,,点为的中点,且平分,,垂足为点
(1)求证:平分;
(2)求证:;
(3)判断,,之间的数量关系,并说明理由.
参考答案
1.C
解:过点作于,如图,
,,
,
和分别平分和,
,,
,
,
,
.
故选:C.
2.B
解:∵BC⊥BD,
∴∠CBD=∠CBE+∠DBE=90°,
∵∠ABE+∠FBE=180°,
∴∠ABE+∠FBE=90°,
∵BD平分∠EBF,
∴∠DBE=∠FBE,
∴∠CBE=∠ABE,
∴BC平分∠ABE,∠ABC=∠EBC,
∵CB平分∠ACE
∴∠ACB=∠ECB,
∵ABCD,
∴∠ABC=∠ECB,
∴∠ACB=∠EBC,
∴ACBE,
∵∠DBC=90°,
∴∠BCD+∠D=90°,
∴①②③正确;
∵根据已知条件不能推出∠DBF=2∠ABC,
∴④错误;
故选B.
3.C
解:作GH⊥AB
由题意可知:BG是∠ABC的角平分线
又∵GH⊥AB,
∴CG=GH
∵
∴GH=2
由直线外一点到直线上各点的连线中,垂线段最短可得:
当点GP⊥AB时,有最小值
即=
GH=2时,最短
故选:C
4.A
解:∵AD平分∠CAB,CD⊥AC,ED⊥AB
∴CD=ED,
∴BC=BD+CD=BD+ED
故选项B正确;
∵AD平分∠CAB
∴∠CAD=∠EAD
∵CD⊥AC,ED⊥AB
∴∠C=∠DEA=90゜
∴∠ADC=∠ADE
即AD平分∠EDC
故选项C正确;
在△ACD中,AC+CD>AD
∴ED+AC>AD
故选项D正确;
若DE平分∠ADB
则有∠BDE=∠ADE
∵∠ADE=∠ADC
∴∠ADE=∠ADC=∠BDE
∵∠ADE+∠ADC+∠BDE=180゜
∴∠BDE=60゜
∴∠B=90゜-∠BDE=30゜
显然这里∠B是不一定为30゜
故选项A错误.
故选:A.
5.B
解:如图所示:
作法:①以为圆心,任意长为半径画弧,交、于点、,
②再分别以、为圆心,大于长为半径画弧,两弧交于点,
③画射线,
射线即为所求.
由作图过程可得用到的三角形全等的判定方法是.
故选:.
6.B
解:过点D作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴CD=DE,
又BD:DC=2:1,BC=9.6cm,
∴DC=9.6÷(2+1)=9.6÷3=3.2cm.
∴DE=DC=3.2cm.
故选B.
7.C
解:如图,作DE⊥AB,
∵平分,
∴DE=CD=2
∴S△ABC=S△ABD+S△DBC=AB×DE+BC×CD=×9×2+×6×2=15
故选C.
8.C
解:由题意可知:BG是∠ABD的角平分线
∴∠ABH=∠DBH
∵
∴∠ABH=∠DHB
∴∠DHB=∠DBH
∵
∴∠DHB=(180°-116°)÷2=32°
故选:C.
9.B
解:过D作DE⊥AB于E,如图,
∵BD是∠ABC的平分线,
∴DE=DC
又∠C=90°,BC=1,AC=2,
∴AB==,
∴S1:S2=AB:BC=:1.
故选:B.
10.B
解:,,,
点在的平分线上,
,
故选:.
11.D
解:过点D作DH⊥BC交BC于点H,如图所示:
∵BD⊥CD,
∴∠BDC=90°,
又∵∠C+∠BDC+∠DBC=180°,
∠ADB+∠A+∠ABD=180°
∠ADB=∠C,∠A=90°,
∴∠ABD=∠CBD,
∴BD是∠ABC的角平分线,
又∵AD⊥AB,DH⊥BC,
∴AD=DH,
又∵AD=4,
∴DH=4,
又∵点D是直线BC外一点,
∴当点P在BC上运动时,点P运动到与点H重合时DP最短,
∴DP≥4,
∴DP的长不可能是3,
故选:D.
12.D
解:①,
,
,
,
,
,①正确;
②平分,
,
,
,
,
,②正确;
③,
,
,
,
由①得,,
,
;③正确;
④,
,
,
,,
,
,④正确,
故选:D.
13.8
解:∵平分,过点作于,,
∴
∴的周长,
∴.
故答案为:8
14.2
解:∵AD平分∠CAB,且∠C=90°,
∴DE=CD=2
故答案为:2.
15.3
解:∵∠ACB=90°,BE平分∠ABC,DE⊥AB,
∴CE=DE,
∴AC=AE+CE=AE+DE=3.
故答案为:3.
16.15.
解:过O作OE⊥AB于E,OF⊥AC于F,连结OA,
∵OB平分∠ABC,OC平分∠ACB,OD⊥BC,
∴OD=OE,OD=OF,
∴OD=OE=OF=cm,
∴S△ABC=S△AOB+S△BOC+S△AOC=cm2.
故答案为15.
17.6
解:当PN⊥OA时,PN的值最小,
∵OC平分∠AOB,PM⊥OB,
∴PM=PN,
∵PM=6,
∴PN的最小值为6.
故答案为:6.
18.作图见解析.
解:作图如下.
详细作图方法如下:
①以点B为圆心,以适当半径画弧,交BA于点D,交BC于点E,
②以点D和点E为圆心,以相等的适当半径画弧,交于点P,
③连结BP并延长,BP即为∠ABC的角平分线.
19.117°
证明:∵,
∴,
∵平分,
∴,
又∵,
∴.
20.见解析.
证明:作交的延长线于,于,于,
平分、平分,
,,
,
又,,
是的外角平分线.
21.见详解
解:(1)∵
∴
∵DA平分∠EDF
∴
∴
∴AE=DE.
(2)∵,DE=DF,AD=AD
∴
∴
∵,DG⊥AB
∴DG=CD.
22.(1)见详解;(2)
(1)证明:∵平分,,
∴,
∵AF=AF,
∴△AFE≌△AFC(ASA),
∴;
(2)解:由(1)可得△AFE≌△AFC,
∴∠AEC=∠ACE,
∵,,
∴∠AEC=∠ACE=40°,
∴.
23.(1)见解析;(2)见解析;(3),理由见解析
证明:∵,平分,OE⊥AC,
∴.
∵点为的中点,
∴,
∴,
∴平分.
证明:在和中,
,
∴,
∴.
同理求出,
∴,
∴.
解:.
理由如下:
∵,
∴.
同理可得.
∵,
∴.
一、单选题
1.如图,,和分别平分和,过点,且与垂直.若,则点到的距离是( )
A.8
B.6
C.4
D.2
2.如图,平分平分,且,下列结论:①平分,②;③;④.其中正确的个数为(
)
A.4个
B.3个
C.2个
D.1个
3.如图,中,,利用尺规在,上分别截取,,使;分别以D,E为圆心、以大于的长为半径作弧,两弧在内交于点F;作射线交于G.若.P为上一动点,则的最小值为(
)
A.无法确定
B.1
C.2
D.4
4.如图,在中,,平分,于E,则下列结论中,不正确的是(
)
A.平分
B.
C.平分
D.
5.一个角的平分线的尺规作法,其理论依据是全等三角形判定定理(
)
A.边角边
B.边边边
C.角角边
D.角边角
6.如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9.6cm,则D到AB的距离为(
)
A.2.2cm
B.3.2cm
C.4.8cm
D.6.4cm
7.如图,在中,平分,且,则的面积是(
)
A.9
B.12
C.15
D.18
8.如图,,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E,F,再分别以点E、F为圆心,大于长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若,则的大小为(
)度.
A.8
B.16
C.32
D.64
9.如图,在△ABC中,∠C=90°,BC=1,AC=2,BD是∠ABC的平分线,设△ABD,△BCD的面积分别是S1,S2,则S1:S2等于( )
A.2:1
B.:1
C.3:2
D.2:
10.如图所示,点在的内部,,,垂足分别为,,,则与的大小关系是(
)
A.
B.
C.
D.无法确定
11.如图,在四边形ABCD中,∠A=∠BDC=90°,∠C=∠ADB,点P是BC边上的一动点,连接DP,若AD=4,则DP的长不可能是( )
A.6
B.5
C.4
D.3
12.如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠EFH;②2∠BEF=∠BAF+∠C;③(∠BAC-∠C);④∠BGH=∠ABE+∠C其中正确的是(
)
A.①②③
B.①③④
C.①②④
D.①②③④
二、填空题
13.如图,在中,,平分,过点作于,若,的周长为11,则______.
14.如图,在中,是的角平分线,,垂足为E,若_______.
15.如图在中,,平分,于,如果,那么________.
16.如图,△ABC的周长为20cm,若∠ABC,ACB的平分线交于点O,且点O到AC边的距离为cm,则△ABC的面积为____________cm2.
17.如图,是的角平分线,点是上一点,于点,点是射线上的一个动点,若,则的最小值为______.
三、解答题
18.如图,已知∠ABC,求作:∠ABC的角平分线BP(不写作法,保留作图痕迹).
19.如图,,平分交于点.若,求的度数.
20.如图,的平分线与的外角平分线相交于点,连接.求证:是的外角平分线.
21.如图,在中,,点D在BC边上,连接AD,点E、F分别为AB边,AC边上的点,连接DE、DF,使得DA平分∠EDF,且DE=DF,过点D作DG⊥AB于点G.
(1)若DFAB,求证:AE=DE;
(2)求证:DG=CD.
22.如图,在中,平分交于点,,分别交,于点,.
(1)求证:;
(2)若,,求的度数.
23.如图,四边形中,,点为的中点,且平分,,垂足为点
(1)求证:平分;
(2)求证:;
(3)判断,,之间的数量关系,并说明理由.
参考答案
1.C
解:过点作于,如图,
,,
,
和分别平分和,
,,
,
,
,
.
故选:C.
2.B
解:∵BC⊥BD,
∴∠CBD=∠CBE+∠DBE=90°,
∵∠ABE+∠FBE=180°,
∴∠ABE+∠FBE=90°,
∵BD平分∠EBF,
∴∠DBE=∠FBE,
∴∠CBE=∠ABE,
∴BC平分∠ABE,∠ABC=∠EBC,
∵CB平分∠ACE
∴∠ACB=∠ECB,
∵ABCD,
∴∠ABC=∠ECB,
∴∠ACB=∠EBC,
∴ACBE,
∵∠DBC=90°,
∴∠BCD+∠D=90°,
∴①②③正确;
∵根据已知条件不能推出∠DBF=2∠ABC,
∴④错误;
故选B.
3.C
解:作GH⊥AB
由题意可知:BG是∠ABC的角平分线
又∵GH⊥AB,
∴CG=GH
∵
∴GH=2
由直线外一点到直线上各点的连线中,垂线段最短可得:
当点GP⊥AB时,有最小值
即=
GH=2时,最短
故选:C
4.A
解:∵AD平分∠CAB,CD⊥AC,ED⊥AB
∴CD=ED,
∴BC=BD+CD=BD+ED
故选项B正确;
∵AD平分∠CAB
∴∠CAD=∠EAD
∵CD⊥AC,ED⊥AB
∴∠C=∠DEA=90゜
∴∠ADC=∠ADE
即AD平分∠EDC
故选项C正确;
在△ACD中,AC+CD>AD
∴ED+AC>AD
故选项D正确;
若DE平分∠ADB
则有∠BDE=∠ADE
∵∠ADE=∠ADC
∴∠ADE=∠ADC=∠BDE
∵∠ADE+∠ADC+∠BDE=180゜
∴∠BDE=60゜
∴∠B=90゜-∠BDE=30゜
显然这里∠B是不一定为30゜
故选项A错误.
故选:A.
5.B
解:如图所示:
作法:①以为圆心,任意长为半径画弧,交、于点、,
②再分别以、为圆心,大于长为半径画弧,两弧交于点,
③画射线,
射线即为所求.
由作图过程可得用到的三角形全等的判定方法是.
故选:.
6.B
解:过点D作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴CD=DE,
又BD:DC=2:1,BC=9.6cm,
∴DC=9.6÷(2+1)=9.6÷3=3.2cm.
∴DE=DC=3.2cm.
故选B.
7.C
解:如图,作DE⊥AB,
∵平分,
∴DE=CD=2
∴S△ABC=S△ABD+S△DBC=AB×DE+BC×CD=×9×2+×6×2=15
故选C.
8.C
解:由题意可知:BG是∠ABD的角平分线
∴∠ABH=∠DBH
∵
∴∠ABH=∠DHB
∴∠DHB=∠DBH
∵
∴∠DHB=(180°-116°)÷2=32°
故选:C.
9.B
解:过D作DE⊥AB于E,如图,
∵BD是∠ABC的平分线,
∴DE=DC
又∠C=90°,BC=1,AC=2,
∴AB==,
∴S1:S2=AB:BC=:1.
故选:B.
10.B
解:,,,
点在的平分线上,
,
故选:.
11.D
解:过点D作DH⊥BC交BC于点H,如图所示:
∵BD⊥CD,
∴∠BDC=90°,
又∵∠C+∠BDC+∠DBC=180°,
∠ADB+∠A+∠ABD=180°
∠ADB=∠C,∠A=90°,
∴∠ABD=∠CBD,
∴BD是∠ABC的角平分线,
又∵AD⊥AB,DH⊥BC,
∴AD=DH,
又∵AD=4,
∴DH=4,
又∵点D是直线BC外一点,
∴当点P在BC上运动时,点P运动到与点H重合时DP最短,
∴DP≥4,
∴DP的长不可能是3,
故选:D.
12.D
解:①,
,
,
,
,
,①正确;
②平分,
,
,
,
,
,②正确;
③,
,
,
,
由①得,,
,
;③正确;
④,
,
,
,,
,
,④正确,
故选:D.
13.8
解:∵平分,过点作于,,
∴
∴的周长,
∴.
故答案为:8
14.2
解:∵AD平分∠CAB,且∠C=90°,
∴DE=CD=2
故答案为:2.
15.3
解:∵∠ACB=90°,BE平分∠ABC,DE⊥AB,
∴CE=DE,
∴AC=AE+CE=AE+DE=3.
故答案为:3.
16.15.
解:过O作OE⊥AB于E,OF⊥AC于F,连结OA,
∵OB平分∠ABC,OC平分∠ACB,OD⊥BC,
∴OD=OE,OD=OF,
∴OD=OE=OF=cm,
∴S△ABC=S△AOB+S△BOC+S△AOC=cm2.
故答案为15.
17.6
解:当PN⊥OA时,PN的值最小,
∵OC平分∠AOB,PM⊥OB,
∴PM=PN,
∵PM=6,
∴PN的最小值为6.
故答案为:6.
18.作图见解析.
解:作图如下.
详细作图方法如下:
①以点B为圆心,以适当半径画弧,交BA于点D,交BC于点E,
②以点D和点E为圆心,以相等的适当半径画弧,交于点P,
③连结BP并延长,BP即为∠ABC的角平分线.
19.117°
证明:∵,
∴,
∵平分,
∴,
又∵,
∴.
20.见解析.
证明:作交的延长线于,于,于,
平分、平分,
,,
,
又,,
是的外角平分线.
21.见详解
解:(1)∵
∴
∵DA平分∠EDF
∴
∴
∴AE=DE.
(2)∵,DE=DF,AD=AD
∴
∴
∵,DG⊥AB
∴DG=CD.
22.(1)见详解;(2)
(1)证明:∵平分,,
∴,
∵AF=AF,
∴△AFE≌△AFC(ASA),
∴;
(2)解:由(1)可得△AFE≌△AFC,
∴∠AEC=∠ACE,
∵,,
∴∠AEC=∠ACE=40°,
∴.
23.(1)见解析;(2)见解析;(3),理由见解析
证明:∵,平分,OE⊥AC,
∴.
∵点为的中点,
∴,
∴,
∴平分.
证明:在和中,
,
∴,
∴.
同理求出,
∴,
∴.
解:.
理由如下:
∵,
∴.
同理可得.
∵,
∴.
