3.2.2 同角三角函数之间的关系课件-湘教版必修2(21张PPT)
文档属性
| 名称 | 3.2.2 同角三角函数之间的关系课件-湘教版必修2(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 237.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-21 20:51:35 | ||
图片预览





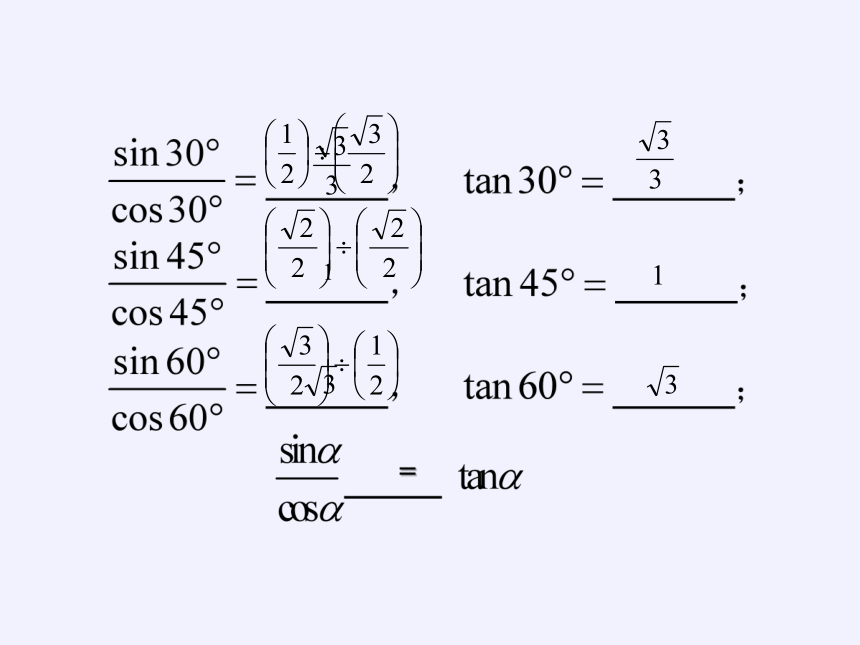
文档简介
3.2.2 同角三角函数之间的关系
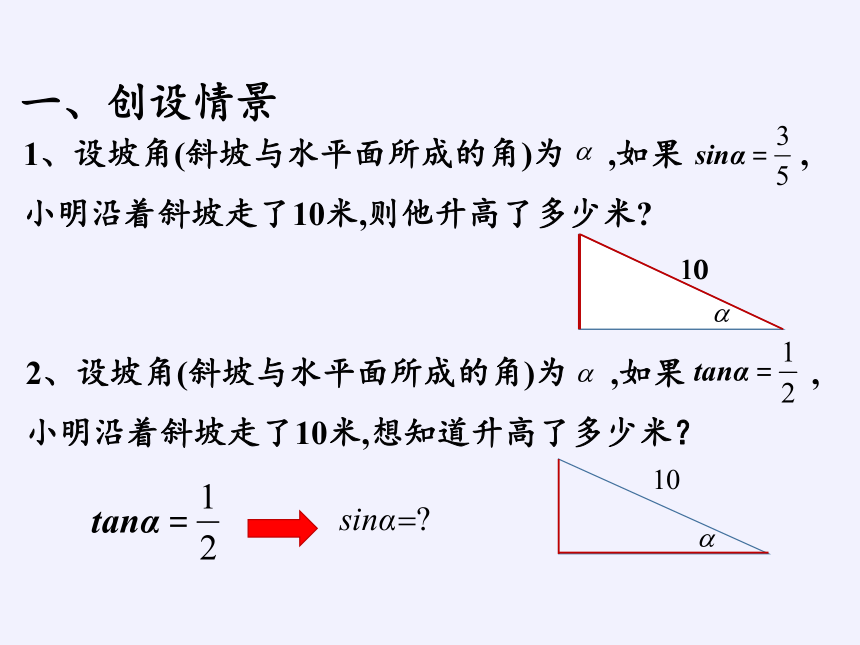
一、创设情景
1、设坡角(斜坡与水平面所成的角)为 ,如果 ,小明沿着斜坡走了10米,则他升高了多少米?
2、设坡角(斜坡与水平面所成的角)为 ,如果 ,小明沿着斜坡走了10米,想知道升高了多少米?
10
10
10
二、学习目标
[知识目标]
1.能根据三角函数的定义导出同角三角函数的基本关系式,
掌握三种基本关系式之间的联系及变形。【重点】
[能力目标]
掌握基本关系式在三个方面的应用:1)已知一个角的三角函数值能求其他三角函数值;2)简单三角恒等式的证明;3)三角函数式的求值运算。【难点】
[情感目标]
培养逻辑推理能力,体验探索的乐趣,增强数学学习兴趣,
培养合作交流、共同探究的良好品质
三、复习回顾
1、任意角的三角函数的定义
设 终边上任意一点 P(x,y),OP=r
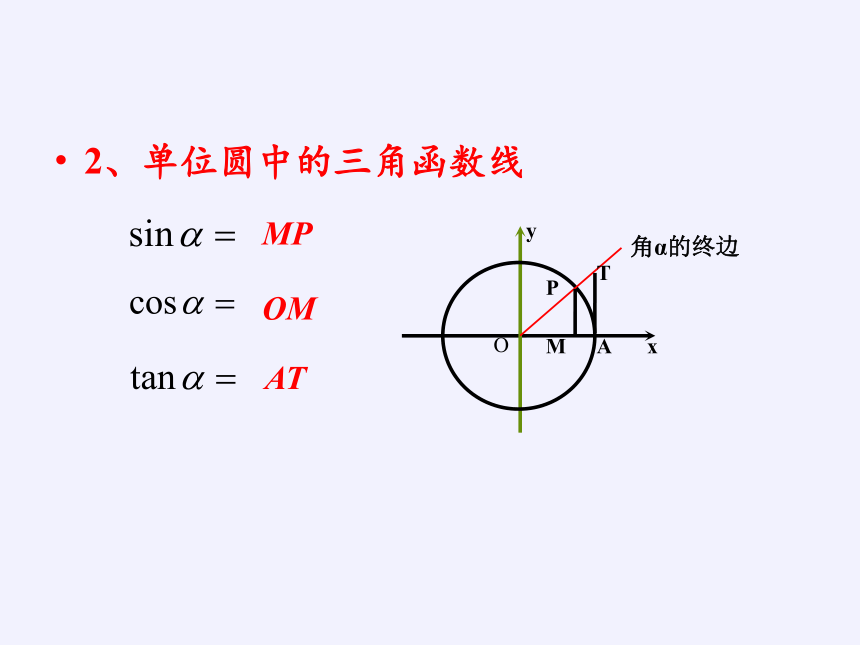
2、单位圆中的三角函数线
x
y
O
角α的终边
P
M
A
T
MP
OM
AT
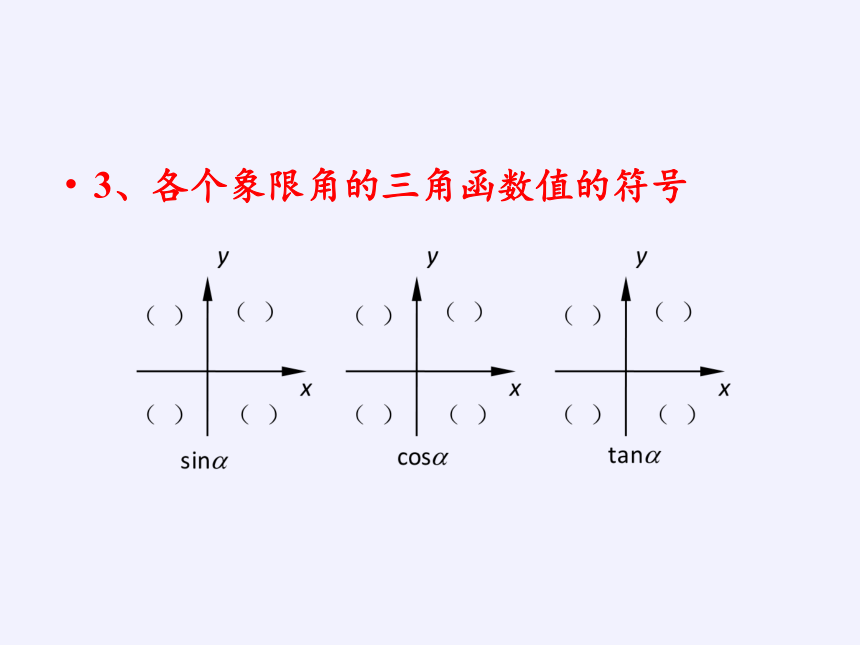
3、各个象限角的三角函数值的符号
一全正
二正弦
四余弦
三正切
x
y
O
sina
+ +
x
y
O
cosa
+
+
x
y
O
tana
- -
-
-
+
+
-
-
全正
7
记忆
四、自主研讨,猜测关系
1
1
=
平方关系:
商数关系:
问题1:这两个关系式对任意角都成立吗?
问题2:这两个关系式能被证明吗?
平方关系:
商数关系:
sin2a + cos2a = (sina)2 + (cosa)2
y
r
x
r
∵ y2 + x2 = r2,
∴ sin2a + cos2a =1 a?R
定义法:
三角函数线法:课本P20页
x
y
O
角α的终边
P
M
A
T
问题3:同角三角函数的基本关系式中的“同角”如何理解?
判断下列式子是否成立?
(2)(3)成立
(1)(4)不成立
1. 公式中的角一定是同角,否则公式可能不成立. 如sin230?+cos260?≠1.
2.同角不用拘泥于形式α, ,6α等等都可以.
问题4:同角三角函数的基本关系式有哪些变形呢?
五、合作探究
以小组为单位,按分配到的题型任务,合作研讨,共同探究导学案里五道题目的解法。(3分钟)
每大组派一名代表上来展示
方法总结
平方关系:
商数关系:
平方关系:
商数关系:
(二)公式的应用:
知一求二:由一个角的某一三角函数值求出其它的两个三角函数值.
(三)数学思想方法:
①分类讨论; ②方程(组)的思想.
(一)基本关系式:
六、课堂小结
七、课后作业
课本P22页第2和第4题
谢 谢
一、创设情景
1、设坡角(斜坡与水平面所成的角)为 ,如果 ,小明沿着斜坡走了10米,则他升高了多少米?
2、设坡角(斜坡与水平面所成的角)为 ,如果 ,小明沿着斜坡走了10米,想知道升高了多少米?
10
10
10
二、学习目标
[知识目标]
1.能根据三角函数的定义导出同角三角函数的基本关系式,
掌握三种基本关系式之间的联系及变形。【重点】
[能力目标]
掌握基本关系式在三个方面的应用:1)已知一个角的三角函数值能求其他三角函数值;2)简单三角恒等式的证明;3)三角函数式的求值运算。【难点】
[情感目标]
培养逻辑推理能力,体验探索的乐趣,增强数学学习兴趣,
培养合作交流、共同探究的良好品质
三、复习回顾
1、任意角的三角函数的定义
设 终边上任意一点 P(x,y),OP=r
2、单位圆中的三角函数线
x
y
O
角α的终边
P
M
A
T
MP
OM
AT
3、各个象限角的三角函数值的符号
一全正
二正弦
四余弦
三正切
x
y
O
sina
+ +
x
y
O
cosa
+
+
x
y
O
tana
- -
-
-
+
+
-
-
全正
7
记忆
四、自主研讨,猜测关系
1
1
=
平方关系:
商数关系:
问题1:这两个关系式对任意角都成立吗?
问题2:这两个关系式能被证明吗?
平方关系:
商数关系:
sin2a + cos2a = (sina)2 + (cosa)2
y
r
x
r
∵ y2 + x2 = r2,
∴ sin2a + cos2a =1 a?R
定义法:
三角函数线法:课本P20页
x
y
O
角α的终边
P
M
A
T
问题3:同角三角函数的基本关系式中的“同角”如何理解?
判断下列式子是否成立?
(2)(3)成立
(1)(4)不成立
1. 公式中的角一定是同角,否则公式可能不成立. 如sin230?+cos260?≠1.
2.同角不用拘泥于形式α, ,6α等等都可以.
问题4:同角三角函数的基本关系式有哪些变形呢?
五、合作探究
以小组为单位,按分配到的题型任务,合作研讨,共同探究导学案里五道题目的解法。(3分钟)
每大组派一名代表上来展示
方法总结
平方关系:
商数关系:
平方关系:
商数关系:
(二)公式的应用:
知一求二:由一个角的某一三角函数值求出其它的两个三角函数值.
(三)数学思想方法:
①分类讨论; ②方程(组)的思想.
(一)基本关系式:
六、课堂小结
七、课后作业
课本P22页第2和第4题
谢 谢
